基于涡流传感器阻抗变化的导电材料缺陷检测

丁鹂,顾文波,崔巍,马倩倩,刘威峰,牛勃

(1.国网宁夏电力有限公司吴忠供电公司,宁夏 吴忠 751100;2.国网宁夏电力有限公司电力科学研究院,宁夏 银川 750011;3.国网宁夏电力有限公司超高压公司,宁夏 银川 750011;4.国网宁夏电力有限公司石嘴山供电公司,宁夏 石嘴山 753000)

0 引 言

高温下导电材料的无损检测是工业应用过程中一个重要的研究方向,相应的检测方法包括机器视觉检测法、涡流检测、超声波法检测、红外热像法检测以及漏磁检测法等[1-5]。其中,涡流检测(eddy current testing,ECT)在复杂结构中具有高灵敏度、高速度以及非接触检测等优点,在航空航天、电力、运输行业中得到了广泛应用[6-7]。涡流的非破坏性,使ECT在导电材料表面的裂缝检测方面表现出色,但是导电材料表面缺陷位置和形状的不同,导致检测过程中磁通量的改变,继而使线圈的阻抗发生变化[8]。通过有限元分析的方法分别模拟不同温度条件下导电材料缺陷区域中涡流的分布,使用阻抗分析仪器对不同温度下测量线圈阻抗的变化进行分析,提出一种通过涡流传感器阻抗变化对高温环境下导电材料表面缺陷进行检测的方法。

1 阻抗检测原理概述

ECT检测原理为基于导电材料和时变磁场源之间的相互作用,当交流电激励线圈组通流时将产生时变磁场,并且该磁场在导电材料中产生涡流和次级磁场,诱导次级磁场影响主磁场的变化。设q为时变电磁场源,p为观察分析点,根据麦克斯韦理论,电磁感应由公式(1)—(4)描述[9-10]。

(1)

(2)

(3)

(4)

式中:J为电流密度;E为电场强度;E1(k),E2(k)分别为一阶和二阶的勒让德椭圆函数;G(p,q)为格林函数;σ(p)为材料电导率;μ0材料介质常数;I(q)为激磁电流;u(p)为激磁电压;k为耦合系数;r(p),r(q)分别为p,q的径向坐标;z(p),z(q)分别为p,q的轴向坐标。

式(1)表示激发电压作用下导电材料产生的电流密度。如果将观察分析点p扩展到一个完整的域Y,则式(1)可扩展为式(5):

(5)

式中:ω为角频率。

由式(5)知当线圈传感器移动到导电材料的表面时将在导电材料表面发生电磁耦合,并产生相应的电磁涡流,此时导电材料的表面状态可以通过线圈阻抗的变化进行分析。相应的耦合等效电路模型如图1所示。

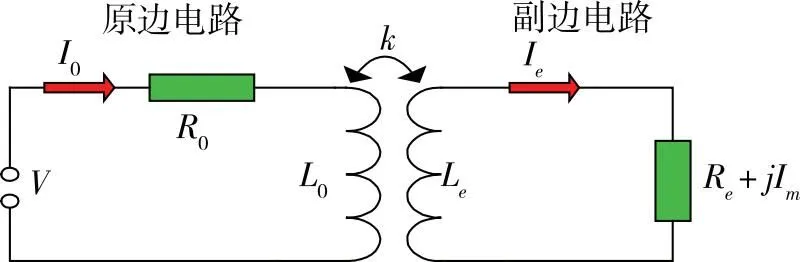
图1 耦合等效电路模型

图1中耦合线圈互感M0=kL0,Me=kLe,ω=2πf,k为回路之间的耦合因子。副边电路阻抗等效为原边阻抗Z′,相应的表达式见式(6)。

(6)

由式(6)可知,导电材料表面涡流效应产生的电抗为容抗,对检测线圈的自身的感抗成削弱作用,从而可以通过副边阻抗的变化来检测金属材料的表面缺陷信息。

2 涡流分布模拟

涡流分布是涡流无损检测的关键,以金属铝为试验导电材料进行涡流分布特性模拟试验,采用标准铝样与带缺陷铝样为样本进行涡流分布分析。

2.1 标准铝样

本文选用标准铝样品的长宽高尺寸为120 mm×100 mm×10 mm,涡流传感器为40圈0.3 mm的线圈,激励电流为100 A。由于线圈和测试件的几何轴呈现对称特性,用2D模型替换3D模型,继而减少有限元分析的计算时间,相应的2D几何模型如图2所示,其中X为缺陷长度,Z为缺陷厚度。

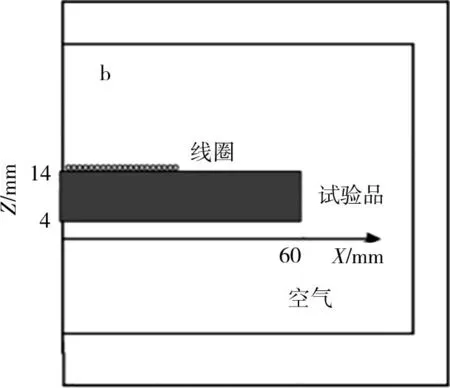
图2 标准模型样品的2D几何模型

根据式(5),通过有限元分析计算感应电流和磁通[量]密度,并根据计算结果分析相应的电磁交换过程。使用频率为2.0 MHz的正弦励磁电流来驱动线圈。

在驱动线圈下方分别绘制点(0,14)到点(60,14)与点(10,14)到点(10,4)的两条直线L,M以及选择点A(10,14)用于对标准铝片的涡流进行分析。其中点A(10,14)处的磁通[量]密度和感应电流变化曲线如图3所示。

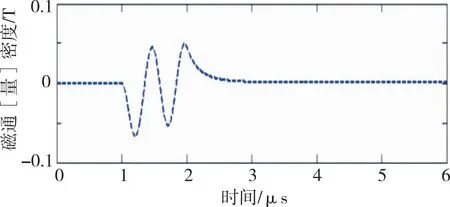
(a)磁通[量]密度变化曲线

由图3知磁通[量]密度变化与激磁感应电流具有相反的方向,随着激磁电流的消失而消失,变化趋势与麦克斯韦定律一致。采用相同的分析方法对线L与线M的感应电流密度进行分析,分析结果见图4。

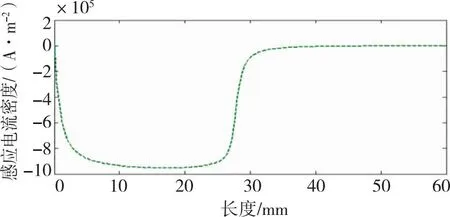
(a)线L的感应电流密度

由图4(a)线L的感应电流密度分析可知,标准铝片感应电流密度主要分布在驱动线圈下方的区域。根据图4(b)线M的感应电流密度分析可知,感应电流密度随标准铝片垂直高度的增加而逐渐降低。

2.2 铝样品不良

工程中常见多层结构中紧固件孔周围发生缺陷,这种裂纹严重影响产品质量。以金属铝为试样研究了表面裂纹缺陷的感应电流分布,相应的带缺陷2D几何模型见图5。

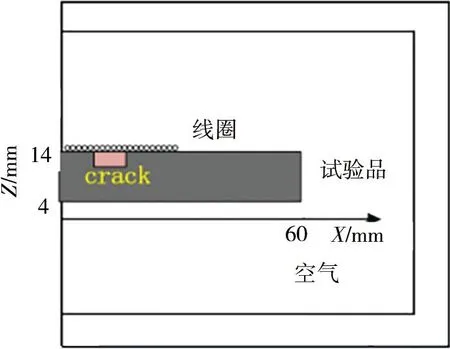
图5 缺陷模型样品的2D几何模型

分析过程中其他物理参数保持不变,通过使用不同电导率的4个缺陷作为样本来分析空间诱导的涡流密度的分布,相应的涡流密度分别见图6。

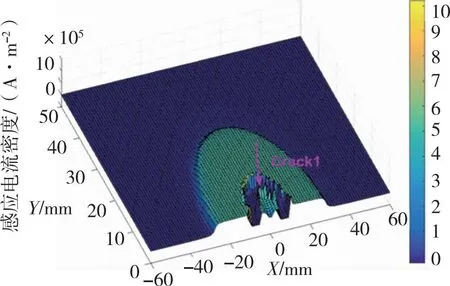
(a)σd=0

通过图6空间诱导涡流密度的分布可知,由于导电性的差异,在样品中缺陷和非缺陷区域密度之间存在很大的感应电流。若缺陷区域的电导率σd>非缺陷区域电导率σc,涡流密度的分布将呈现凸起的形状,最终导致检测线圈阻抗的增加;若σd=σc,涡流密度的分布不会改变,否则,如果σd<σc,感应电涡流空间分布呈现凹形状,使检测线圈阻抗变小。图7显示了在不同电导率条件(t=5.5 μs)下从点(0,14)到点(60,14)的线N的诱导涡流密度的分布。

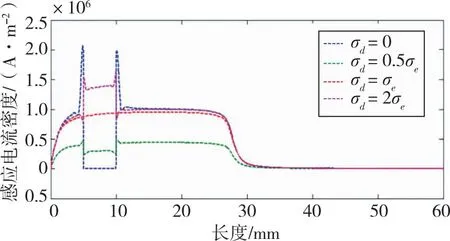
图7 线N在不同的电导率条件下涡流密度分布

不同电导率条件下涡流密度分布的不同是由于激励电流产生的交变磁场与感应电涡流产生的二次磁场之间的相互作用所引起的,最终通过线圈阻抗的变化展示出来,从而可以通过线圈阻抗变化来对被试材料的缺陷进行检测。

3 缺陷测试

3.1 缺陷测试平台设计

本文缺陷测试系统如图8所示,主要包括阻抗分析仪6379、温度传感器、涡流传感器以及电阻烘箱对高温环境样品表面缺陷进行测试。

图8 高温下缺陷检测系统

图8中,电涡流检测的激励线圈采用半径为40 μm,圈数为35,材料为铜的螺线型线圈。考虑到圆形和裂纹缺陷在其涡流密度分布中的相似性,使用图9的裂纹缺陷代替圆形缺陷以简化模型并减少数据量。

图9 被试导电材料

3.2 常温下涡流传感器的表面检测

25 ℃常温下对测试材料表面从左到右扫描,扫描过程中当远离缺陷时探头移动步长设为5 mm,当靠近缺陷时相应的探头移动步长调整为2 mm。采用阻抗分析仪对不同位置的阻抗变化进行分析,测试材料表面的不同位置接收线圈的相位和阻抗的变化趋势见图10。

(a)相位变化

标准铝样与带缺陷铝样表面的阻抗差异很大,其中在缺陷区域线圈阻抗最大,且阻抗变化比相位变化更敏感。在非缺陷区域的阻抗变化可以通过铝样表面电导率的差异来解释,因此,使用阻抗和相位变化可以精确地对导电材料进行缺陷检测。

3.3 不同温度下的表面裂纹缺陷测试

采用图8缺陷检测系统在150 ℃的稳定温度下对导电材料表面缺陷进行检测。选择从测试件表面上的点(0,10)到(85,10)的线P进行测试分析接收线圈的阻抗相位和幅值的变化(见图11)。

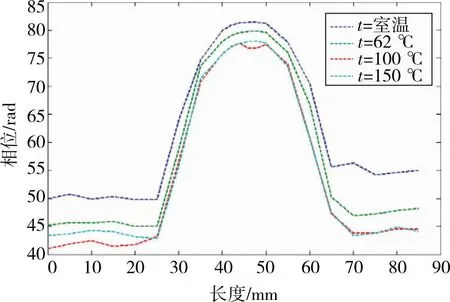
(a)相位变化

环境温度从常温升至100 ℃时,线圈阻抗的相位变化比幅值变化更为明显,且相位随着温度的升高而逐渐降低。然而,在100～150 ℃时,由于被试材料性能参数的不同,导致线圈阻抗的幅值和相位变化不明显,因此在高温环境下使用电阻敏感的材料制造接收线圈,通过涡流检测的方法可以对导电材料的表面缺陷进行检测。

4 结 论

常温与高温环境下导电材料表面缺陷的裂纹缺陷可与涡流密度分布特征相关。通过测试试件表面裂纹缺陷的阻抗幅值和相位变化进行分析。高温环境下使用电阻敏感的材料制造接收线圈,采用涡流检测的方法对导电材料的表面裂纹缺陷进行检测,并给出了高温环境下涡流检测导电材料表面裂纹缺陷的判断方法。