风-储孤岛微电网的虚拟同步电机模型预测频率波动抑制

罗美玲,韩忠修,黄伟兵,赫嘉楠,寿邵安

(1.国网宁夏电力有限公司,宁夏 银川 750001;2.国电南瑞南京控制系统有限公司,江苏 南京 211100;3.国网宁夏电力有限公司电力科学研究院,宁夏 银川 750011)

0 引 言

近年来,能源危机逐渐加剧,可再生能源重要性日趋显著。风电并网渗透率快速增加,电力系统越来越电力电子化[1-3],大量风机运行时频率波动频繁,导致风机发电的稳定性受到影响。由于风速不确定和随机性的特点,风机发电量通常会受到不规则变化的影响。此外,随着风速的降低,功率输出支撑也需要相应地增加备用功率,以确保风力发电机组的正常运转,储能系统是解决该问题的一个良好方案,然而,储能系统的容量和成本限制以及体积问题,使得功率无法长时间得到补充,这将导致难以实现持续的功率补偿[4-6]。为了解决这一问题,文献[7]提出了仅在风速在额定值附近波动时进行功率补充或吸收的方法,以减小风-储孤岛微电网系统频率波动的影响[8-11]。

预测控制是近年来发展非常良好的一种控制技术,因其具备多步预测、多目标控制、滚动优化等优点,目前已经被广泛应用于电机驱动[12-13]、微电网系统能量管理、新能源电力电子系统控制中[14-17]。考虑到模型预测控制具有的上述优点,提出一种基于模型预测控制的虚拟同步电机来实现风-储发电系统频率波动抑制。

为实现频率波动抑制,本文开展以下研究:首先,介绍模型预测控制的基本原理;其次,提出采用模型预测控制改进目前的虚拟同步电机(virtual synchronous generator,VSG)控制方法,结合两者的优势实现模型预测-虚拟同步电机(model predictive control-virtual synchronous generator,MPC-VSG)控制并给出其实施步骤;最后,为了验证提出方法的正确性和可行性,采用工况一模拟风力发电系统功率波动时MPC-VSG的控制效果,采用工况二模拟微网中负载功率波动时的频率稳定减小控制效果。

1 提出方案

1.1 MPC-VSG控制策略

传统的VSG模拟了同步电机的特性,通过2个下垂环节和1个旋转方程支撑孤岛微电网频率[18-23],同时向系统提供阻尼。由于VSG中参数是固定的,其频率控制效果往往有限。 因此,基于现有的VSG思想方法,提出了引入模型预测控制理论的新方法。该方法通过建立系统的预测模型来实现控制,同时考虑多种输入和不同类型的输入输出约束,并通过求解二次函数使目标函数最小化,以获得最优的控制量。此外,MPC可以同时实现多个目标的协同优化控制,也便于添加新的控制目标。本文构建了虚拟同步电机的预测模型,以获得频率波动时连接点功率变化的增加。同时,采用MPC获得的最优功率变化,通过实时将虚拟同步电机的功率修改为指令值,并根据预测值进行调整,实现了相对较大的功率补偿,达到降低风-储孤岛微电网系统频率波动的目的。

图1为MPC-VSG控制框图,该控制策略作用于储能变流器。目前,大多数可变速风电场的VSG的实现方式包括旋转方程用于惯性模拟,并且引入有功和无功功率2个下垂控制器。这里通过设计1个MPC控制器来实时调整VSG的功率指令值,减小微网公共接入点电压的频率波动,形成1种新的MPC-VSG控制方法。

图1 MPC-VSG控制

1.2 模型预测控制理论基础

MPC的主要思想[20]可以具体描述如下:在采样时刻k,根据当前时刻的采样值,结合构建的状态空间数学模型,围绕控制目标设计代价函数,求解代价函数最小时的控制量。这个问题的求解是1个优化过程,需要考虑输入和输出的约束条件,然后从得到的多个最优控制量中选择第1个控制量来应用于被控对象,反复迭代执行,以实现所期望的控制目标跟踪性能,并实现多目标协同优化。

假设1个一般的离散系统的状态空间增量方程可以表示如下:

(1)

式中:Δx(k)为状态变量增量,Δu(k)为输入控制量,yc(k)为被控输出量,Δd(k)为外部干扰量增量,A、Bu、Bd、Cc分别为连续系统转化为离散系统后的系数矩阵、控制矩阵、扰动系数矩阵、状态变量输出系数矩阵。

这里以式(1)的单步预测为例,可以通过k时刻测量值,得到k+1时刻状态量的增量。

Δx(k+1|k)=AΔx(k)+BuΔu(k)+

BdΔd(k)

(2)

基于式(2)可以根据状态方程得到输出量的预测值,如式(3)所示:

yc(k+1|k)=CcΔx(k+1|k)+yc(k)

=CcAΔx(k)+CcBuΔu(k)+CcBdΔd(k)+yc(k)

(3)

为了实现控制系统输出yc跟踪参考输入,可以将代价函数J设计为如式(4)所示:

J=(yc(k+1|k)-r(k+1))2

(4)

若系统输入和输出控制变量没有输入输出条件约束,则可以计算得到当系统总代价函数取得最小值时,控制量的增量为

(5)

这样即可以将需要的控制增量设置为式(5),以实现尽可能跟踪输入指令的效果。这是模型预测控制的主要思想。在具体应用实践中,可以通过根据系统的实际情况,设置不同的输入和输出约束条件,得到不同的控制效果,这样系统的最优解的求解过程将变为求解1个带约束的二次规划问题。

2 风-储孤岛微电网MPC-VSG控制方法

考虑到大规模风-光-储发电系统安装成本较高,难以实现每个风机安装1个储能装置,故选择将储能装置接在公共交流母线汇合处。通过设计储能系统的控制方案实现公共接入点频率动态响应优化目的,提高系统的惯性。

2.1 MPC-VSG预测控制器设计

图1为VSG控制。旋转方程是影响控制策略惯性的关键,建立旋转方程的数学模型可以通过测量公共接入点电压频率来预测有功功率变化的补偿量,并将其作为系统的控制量,以减小频率波动的目标。虚拟同步电机的状态空间模型参考式(6)。

(6)

式中:ω=ωm-ω0,D为阻尼,Pm为输出功率,Pe为额定功率。

由此得到旋转方程如图2所示。

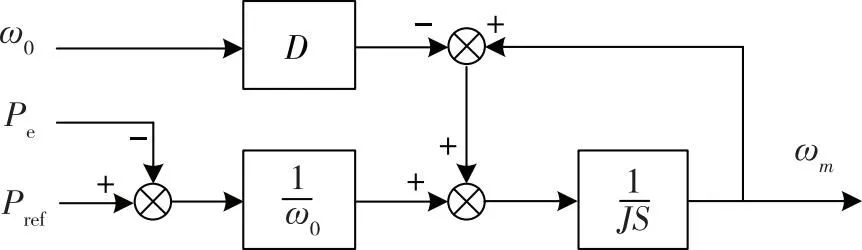
图2 旋转方程

接下来的设计步骤如下:

第一步,采用Du Hamel方法将连续系统离散化,Ts为系统的采样时间,将式(6)转化为离散模型得到:

(7)

(8)

第二步,引入积分减少静态误差,将式(7)改写为增量模型。

(9)

式中:

(10)

根据1.2节介绍的模型预测控制思想,以当前时刻的测量值为初始条件,基于状态空间预测模型式(7)来不断预测未来状态系统变量值。在这里假设预测的时域为p,而系统的控制时域为n。这意味着利用预测模型来预测从当前时刻开始的未来p个时刻的状态变量值,并在每个时刻进行控制决策,且满足n≤p,并假设以下条件成立:

1)在控制时域之外的时刻,控制量ΔPm保持不变,即ΔPm(k+i)=0,i=n,n+1,…,p-1;

2)可测干扰在k时刻之后不变,即ΔPe(k+i)=0,i=1,2,…,p-1。

对于p步预测,可以得到PCC处频率预测误差。

Δω(k+n|k)=AΔω(k+n-1|k)+BmΔPm(k+
n-1)+BeΔPe(k+n-1)=
AnΔω(k)+An-1BmΔPm(k)+
An-2BmΔPm(k+1)+…+
BmΔPm(k+n-1)+
Am-1BeΔPe(k+n-1)

(11)

第三步,根据输出方程,得到p步输出可以表示为

y(k+p|k)=y(k+p-1|k)+Δω(k+p|k)

(12)

对于模型预测控制来讲,较短的预测步长难以达到良好的补偿效果,但是较长的预测步长却会带来复杂的计算工作量,同时处理器的内存占有率也会大幅度增加。因此,在综合考虑嵌入式处理器负荷、计算量和预测精度后,预测步长选择3步预测作为控制补偿量,式(12)将变为

Yp,c(k+1|k)=SAΔω(k)+Iy(k)+SeΔPe(k)+SmΔPm(k)

(13)

式中:I为单位矩阵。

接下来考虑约束函数设计,将代价函数设置为虚拟同步机额定功率变化ΔPm及系统的频率偏差Δω加权平方和最小,表示为

(βΔPm(k+i|k))2]

(15)

将公共接入点处的频率波动限制在一定范围,在考虑频率和功率变换约束后,MPC优化问题可以描述为

(16)

满足系统动力学(i=0,1,…,p)。

并且y(k)需满足输出的时域约束

ymin(k)≤y(k)≤ymax(k),∀k≥0

(18)

式中:Jp(ω(k),ΔPm(k))为系统的代价函数,可以表示为

(19)

式中:Γy和ΓPm为加权矩阵,Γy=diag{α,α,α},ΓPm=diag{β,β,β};α和β分别为公共接入点处的频率偏差和功率变化的权重系数;R(k+1)为控制输出参考序列,由于期望的频率变化为0,因此这里设置为R(k+1)=[0 0 0]T;ΔPm(k)是控制量增量序列,为约束优化问题的独立变量,定义为

Yp,c(k+1|k)为k时刻基于模型预测控制的VSG的3步控制输出,定义为

考虑到实践中的输入和输出约束,通常无法得到优化式(16)的解析解,因此采用数值求解法。将式(19)转化为ZTHz-gTz的形式,其中z=ΔPm(k)是独立变量。将多步预测式(13)带入式(19),中间变量被定义为

Iy(k)-SeΔPe(k)

(22)

式(19)可以表示为如式(23):

(23)

因为Ep(k+1|k)TΓyTΓyEp(k+1|k)与独立变量ΔPm(k)无关,所以式(23)可以等价为

Jp=ΔPm(k)THΔPm(k)-G(k+1|k)TΔPm(k)

(24)

式中:

H=SmTΓyTΓySm+ΓPmTΓPmG(k+1|k)=2SmTΓyTΓyEp(k+1|k)

(25)

将输出约束式(18)转化为Cz≥b的形式,则输出约束可以表示为

Ymin(k+1)≤Yp,c(k+1|k)≤Ymax(k+1)

(26)

式中:

将式(13)带入式(22)中,输出约束可以转化为

(28)

综合式(16)、式(17)和式(28),带约束的MPC优化问题可以表示为以下形式的二次规划问题:

满足CmΔPm(k)≥b(k+1|k)

(29)

式中:ΔPm为有功功率变化值,H和G(k+1|k)由式(25)给出,Cm=[-SmSm]T,b(k+1|k)如式(30)所示。

(30)

式中:Ymin为输出约束最小值,Ymax为输出约束最大值。

2.2 执行流程分析

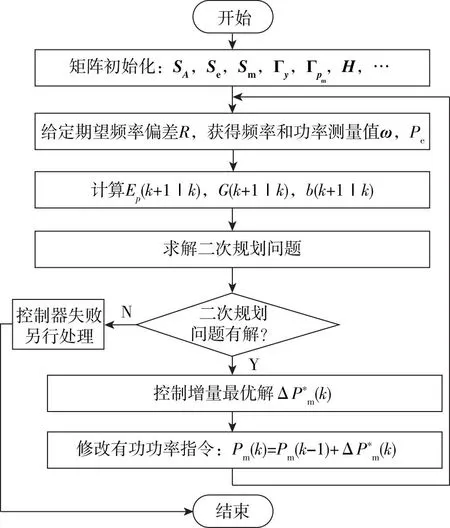
图3 MPC-VSG控制方案执行流程

2.3 最优解求取

对于前面所提出的MPC-VSG控制方案,考虑到存在非线性的不等式约束,为了简化分析,可以将其分解为2种情况。

第一种情况:式(29)的解在可行域边界内,原模型可以简化为无约束模型。可以定义中间变量为

(32)

则约束函数可以重新表示为

Jp(Δω(k),ΔPm(k))=ρTρ

(33)

将式(13)代入式(32)可以得到

Axz-bx

(34)

其中,

(35)

当式(29)取得极值时,需满足的条件见式(36)。

(36)

由此得到控制变量的最优解z*,将其表示为

(37)

(38)

其中,

KMPC=[1 0 0](SmTΓyTΓySm+ΓPmTΓPm)-1×SmTΓyTΓy

(39)

代入式(9),并将ω(k)=ω(k-1)+Δω(k)代入,可以得到闭环控制系统的表达式:

Δω(k+1)=(A-BmKMPC(SA+I))Δω(k)+
BuKMPCR(k+1)+(Be-
BmKMPCSe)ΔPe(k)-BmKMPCIω(k-1)

(40)

当A-BmKMPC(SA+I)的绝对值小于1时,PCC点处的Δω可以收敛至0,则可以证明闭环系统式(40)是名义渐近稳定[21]。

|A-BmKMPC(SA+I)|<1

(41)

第二种情况:式(29)的解在可行域边界上,此时,模型预测控制器将根据设定的上限值输出功率,图1中P-f下垂控制部分将负责系统的频率调整,并决定系统的频率稳定性。

3 方案验证

为了验证所提出的MPC-VSG在风力发电系统孤岛微电网系统中的有效性,本文进行了半物理仿真。工况一主要验证了当风电输入波动时,比较MPC-VSG控制方法和传统虚拟同步电机无功率补偿的VSG控制策略,观察在减小系统频率波动方面的优化效果。工况二被用来验证MPC-VSG控制方法在风-储孤岛微电网下对负载变化导致的功率波动的频率支撑效果。

3.1 工况一

该工况的系统结构与图1一致,模拟了永磁直驱风-储孤岛微电网的实际运行工况,如图4所示。

图4 某市1周的风速波动

参考某市2022年12月18日到24日之间的风速数据进行数值模拟验证测试。考虑到气象数据网上的风速的更新速度为1次/h,故采用式(42)进行随机风速模拟。

vrand=vmaxrand(-1,1)cos(ωv+φv)

(42)

式中:vrand表示为随机风速,vmax表示为随机风速最大值,ωv表示为风速波动平均距离,φv定义为0～2π的随机量。

根据式(42),可以利用对某市风速资料的观测,将随机风速的波动范围设定为±2 m/s,并生成每秒的随机风速数据,然后可以通过线性插值和拟合获得连续的风速曲线。在仿真中,可以将时间t=10 s的风速设置为随机风,并采用不同的控制策略来控制储能系统。

在模拟中设定的风速如图5所示。在t=10 s之前,风速保持为风机的额定风速。由于负载的功率被设置为与风机的功率相同,因此风机在10 s前以最大功率点跟踪控制运行模式工作,控制系统将根据其最大功率进行输出,以实现并网风能的最高效率。此时,系统中的虚拟同步电机也将根据其额定功率输出提供给负载,在系统的公共连接点处的PCC频率稳定在50 Hz左右。

图5 模拟风速波动曲线

当t=10 s时,当风速曲线变为随机风时,风能波动会导致风机的输出功率波动。考虑到系统PCC点频率与有功功率变化之间的关系,PCC处的频率波动会发生波动。图6显示了系统公共接入点在不同控制策略下频率波动的波形变化,“NO-VSG”表示仅当同步电机和风机在系统中运行时系统的频率波动,“VSG”表示使用虚拟同步电机的储能系统(energy storage system,ESS)控制方法,“MPC-VSG”表示当储能装置采用MPC-VSG控制方法时系统在PCC处的频率波动。

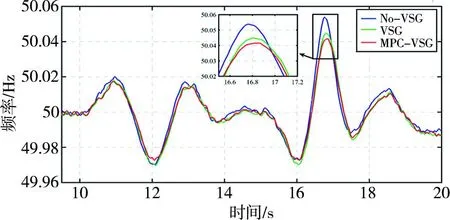
图6 不同仿真条件下系统PCC处的频率波动波形

系统未连接储能装置时PCC处的最大频率波动为0.054 Hz,采用传统无功补偿VSG控制方式时PCC处最大频率波动Δf为0.047 Hz,采用本文提出的MPC-VSG控制方法时PCC处的最大频率波动Δf为0.044 Hz。与传统的VSG控制方法相比,本文提出的模型预测控制补偿VSG策略可使系统频率波动降低6.4%。这些结果表明,MPC-VSG方法具有明显的优势。

3.2 工况二

为了验证MPC-VSG控制方案在改变永磁直驱同步发电机风-储孤岛微电网系统负载端功率,拆除永磁直驱动风机发电部分时的优势,储能ESS系统与同步电机SG并联运行,以模拟系统岛微电网的运行状态。该系统的结构如图7所示,通过开关负载2(这里主要考虑电阻负载)来模拟不同负载条件下的频率波动。将MPC-VSG方案和其他方案分别应用于孤立网络系统,比较不同控制方案对频率波动的抑制效果。

图7 风-储孤岛微电网模拟系统

半实物仿真环境平台搭建中,储能装置ESS和同步发电机SG同时向负载供电。系统的工作状态为在8 s前同步电机单独对1台功率为15 kW的阻性负载1,在t=8 s时,接入1台功率为5 kW的阻性负载2,在t=16 s时切除负载2。

风-储孤岛微电网系统中,同步发电机和储能装置的参数设置情况如表1和表2所示。

表1 永磁同步发电机参数配置

表2 虚拟同步发电机参数配置

图8分别显示了VSG和同步电机的输出功率。可以看出,当储能电池组系统装置连接且负载发生变化时,储能装置可以在控制系统的作用下提供负载变化所需的额外功率来支撑负载,降低系统中同步电机的瞬时输出,缓解同步电机的输出压力,并使同步电动机的输出功率平稳过渡。当负载不变时,采用MPC-VSG储能系统不工作;当负载突然变化时,储能系统ESS可以提供更高的瞬时功率以实现功率支持,使同步电机的输出功率平滑,并减少其输出波动;因此所提出的MPC-VSG方法不需要配备大容量储能系统,仅在需要瞬时功率时根据模型预测控制输出设置,因此该方案将大大降低系统成本。

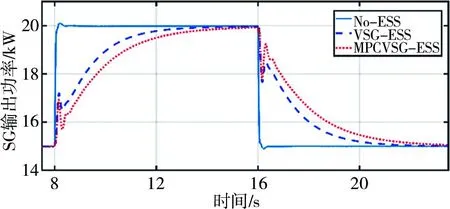
(a)同步发电机

图9显示了系统负载变化期间风-储孤岛微电网PCC的频率和频率变化率。由于储能系统没有ESS支撑,系统的惯性支撑效应相对较低,导致频率波动较大(最大值为0.68 Hz),频率变化率的最大值为2.27 Hz/s。ESS采用传统的VSG控制时可以有效地提高系统频率的惯性,将频率波动降低到0.25 Hz,频率变化率降低到0.74 Hz/s,并缩短系统恢复时间。储能系统采用MPC-VSG-ESS时频率波动降低到0.18 Hz,比传统的VSG-ESS方法减少了约24%。频率变化率也降低到0.58 Hz/s,与VSG-ESS相比降低了约22%。因此,半物理仿真结果表明,MPC-VSG方法可以最大限度地提高风-储孤岛微电网系统的惯性,减少系统在公共接入点PCC处的频率波动,有效提高风-储孤岛微电网系统的频率稳定性。

(a)频率波动

4 结 论

针对大型风电并网引起的频率稳定性问题,提出了1种带约束的MPC-VSG控制方法:首先,给出了连续控制集模型预测控制理论的基本思想及其相关方程,根据风-储孤岛微电网系统的频率稳定性问题,将虚拟同步电机应用于储能系统,构建了虚拟同步电机的旋转方程,并通过多步预测推导出预测模型。选择系统的约束条件为功率变化和频率变化,通过三步预测得到VSG的输出功率与频率变化之间的关系;其次,通过求解二次规划问题,以最优补偿量调整额定有功功率,从而增加风-储孤岛微电网系统的惯性,减少风-储孤岛微电网系统的频率波动,提高系统的频率稳定性;最后,验证了该方法的优点,结果表明MPC-VSG在抑制频率波动方面优于传统方法。