立体车库出入库路径规划优化算法

高云飞　朱霄霄　刘军　徐耀婷　金耀花

摘 要：目前，伴随着中国的发展，人们的生活质量也有了显著的提升，我国的私人汽车也越来越多。随着我国城镇私人汽车拥有量的不断增加，我国城镇居民的“停车难”问题已经成为当前急需解决的一大难题，也是当前我国城镇居民面临的迫切需求。当前，国内的立体停车设施普遍面临着停车周期长，运营效率低，维护成本高等问题，使其很难在中小城市得到普及。造成这一问题的主要原因是，立体停车场的自动测量和控制是一项集成了机电、光学和计算等多个领域的交叉技术，它的研究和实施都有很大的困难。在这些问题中，最重要的是对立体停车场进行有效的调控和优化。另外，由于我国中小城镇居民对立体停车设施的认可度较差，使得整个市场出现了“有价无市”的局面。为了改善和解决在现阶段，在三维车库的测控管理中存在的上述问题，本文就是要对三维车库的测控方法和优化策略进行讨论和分析，重点是对排队模型的构建和路线优化算法的实现进行研究。

关键词：立体车库 车库数字化建模 最优路径规划 融合算法 排队调度

1 引言

“停車难”的问题会对城市居民的日常生活产生直接的影响，因此，为了更好地解决与之有关的“停车”问题，许多城市都采用了“立体车库”来代替目前的“常规”方式[1]。当前，我国的立体车库的发展已经步入到了一个新的时期，它使用的是自动控制车辆的出入，而且它的占地面积很小，可以很好的利用了城市的三维空间，还可以进行多层次的停车，对车辆的出库和入库管理非常方便快捷，车辆安全系数高，防盗措施好，可以灵活的分配资源等一系列的优点。立体车库属于一种先进的停车设备，它占据的土地很少，所以它在现代化的停车设备中得到了大量的使用。不过，随着人类社会的发展，这些技术的进步，对泊位的需求也会越来越大。从目前的计划来看，整个计划的进度已经完成了50%。因此，操作的有效性对工作的有效性有很大的影响[2]。如何有效地降低算法的执行速度，缩短算法的执行速度，已成为当前研究人员关注的重点。

2 建立数字化模型

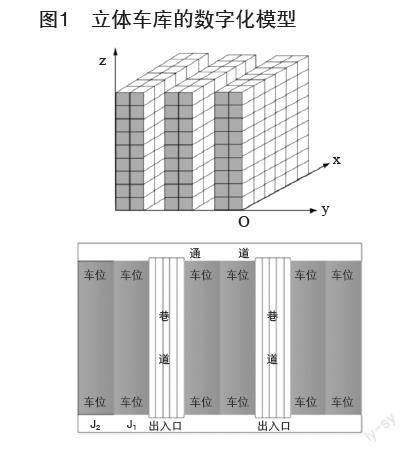
此类车库参照实际的泊车位分布信息，能够准确划分成两个基础分类。我们用到立体车库数字化模型建立地理拓扑结构，需要建立一个拓扑结构数字化模型，我们定义空间坐标系xyz，车位为a，巷道为b，空余车位为c，层数为d，具体数字化模型结构为（1，1，a，b，c，d），它可以准确表述各个位置的地理拓扑结构[3]。

3 立体车库排队模型分析

在研究过程中，由于系统内排队类型和系统外实际抵达车辆数量存在差异，因此，在研究过程中，选择系统内排队模型。

根据目前的停车场模式，在两种情况下，分别采用M/M/1/0/0 N客户来源有限类型和M/M 1/1/N/0，建立了停车场中的队列模式，并以客户平均等候时间，平均等候长度，停车位空闲率为度量指标，对其进行了模拟和分析[4]。

（1）在客户来源数量为25，32，50，75，100的时候，对于客户来源的数量是25，32，50，75，100个客户来源是有限的，根据客户来源数量的限制，分别对客户来源的各种情形进行了仿真，得到了平均等待时间，平均等待队长，堆垛机的空闲率，并与之比较。

（2）M/M/1 N/0无穷大的系统的能力限制类型。

对于网络的服务能力为2，3，4，5的情形，在网络的限制下，分别进行了网络的仿真[5]。通过对客户平均等候时间、平均等候队长长度以及堆积器空闲率三个参数的仿真。

4 排队论模型

排队论（Queuing Theory），也被称为“随机状态下的服务系统”，是一种用来研究服务对象中的随机聚集与消融规则以及服务系统中的随机工作过程的一种数学理论与方法。主要包括以下三个方面：

（1）性别差异。在不同的模式下，对不同的服务体系进行了讨论。是对队长队列随机分布、队列等待时间随机分布和忙期规律分布等进行的研究，主要包含了两种情况：即时时态和平稳时态。

（2）最优解。一种是对队列系统进行最优的静态最优。二指在已有的队列中，对最优操作进行了动态最优优化。

（3）基于概率论的队列模型。为了确定特定的排队系统的统计规则与何种特定的排队模型相一致，可以依据对应的排队系统的对应的排队理论，对其进行统计分析和研究。排队理论中的最少控制问题由三个部分组成：输入程序，排队规则，服务组织。

3.1 排队论系统组成函数

（1）输入法：顾客进入队列的规则。指在某一时段中，抵达该区域的顾客数目，或者是两位顾客先后抵达的时间。程序大体可分为两类：确定性程序和随机程序。被判定为一段时间内不连续的输入。当顾客抵达次数n（t）满足某一特定条件时，顾客抵达次数n（t）满足随机分布。大多数情况下是齐次的Poisson型和负性的指标型的情况。如果符合齐次Poisson分布，则在t时刻期间，达到n个顾客的可能性方程为：

（1）

相继到达的客户的间隔时间遵从负指数函数条件下分布函数如式（2）所示。

（2）

λ称为客户平均到达率，即单位时间内客户到达当前服务系统数期望值；1/2即为客户到达平均间隔时间。本文主要讨论服从泊松分布的客户输入。

（2）队列原则有三种：原地等候原则、顾客损失原则以及两者的结合原则。

（a）“现场等”制度，即顾客抵达目前的队列系统，在排队时，所有能够提供服务的服务点恰好被前面的顾客占据，或是该服务点还没有提供目前顾客的服务，那么后面的顾客就必须在队列中等待。在等待制中，服务的次序可以按照先到先服务，也就是先来后到，也可以设定后到先服务，或可以随机地服务某一客户，并给某些客户有一定的优先权服务。

（b）顾客流失法：顾客到达时，如果发现整个系统中的服务组织都处于待命状态，则会立即退出现有的队列。

（c）这两种混合系统是一种等待系统和一种失去系统的结合[7]。由于系统为用户预留的等候位置是有限制的，所以如果用户数量超出了系统所允许的最大容量，那么用户将会被强制退出目前的队列。

（3）所述服务机构可以是一个或者若干个独立的服务平台，在所述系统中，所述服务平台也可以是一个叠置器。可以并行或串联多个帮助平台。通常情况下，服务时间可划分为两种类型：确定型和随机型。大部分的随机者的服役时间都符合负值的指数分布。

（3）

式中μ为服务组织服务率的期望，为服务组织的服务时间期望。

5 立体车库路径出入库优化算法研究

5.1 路径规划Floyd算法

Floyd演算法是在一个已知权重的图谱上，在多个数据源中，找到一个数据源间的最短路，从而得到一个数据源间的最短路。航迹最优是指航迹从起点i至终点j的一条最优航迹。由任一结点i至任一结点j之间的最近距离只有两个选择：一是从任一结点i至任一结点j之间不需通过其他结点；二是由点i通过几个结点k到达点j。该算法最初假定Dis（i，k）是从一个结点k到另一个结点的最短路径的距离[6]。

（4）

在将该通路中的全部结点k遍历完毕时，起始点i至目标点j之间的最短通路的距離被记录在Dis（ij）中。Floyd方法的主要思想是利用一条有向图中权函数的通路矩阵来寻找两条通路之间的最短路。从图的带权邻接矩阵出发，对其进行n次路径更新，那么从矩阵D（0）=4，根据公式，可以构建出矩阵D（1）。然后，从D（n-1）出发，利用相同的计算方法，得到新的路径矩阵D（n）。矩阵D（n）的i行j列的元素就是从i号起点到j号目标点的最短路径的长度，那么，将D（n）称为图的最短路径距离矩阵[7]。在此基础上，提出了一种计算两点之间最短路的方法。状态转移方程见式（5）。

（5）

式中表示i到j的最短距离，k是穷举i，j之间的全部断点，初值应该为0。

4.2 融合算法设计

（1）融合算法设计步骤。

（a）按照Floyd的现有状态，按照三维车库模型设置了该融合算法的操作参数，并在Floyd的现有状态下，随机生成一个初值解x。在禁止列表中清除全部的数据[8]。

（b）对目前的状况进行判定，在期望的状况下，最短路的状况是否符合最短路的状况。如果是的话，那么该算法就会被终止并且被跳出来，从而得到最优的结果；如果没有，请按照下面的方法执行。

（c）使用目前的融合态数值的邻居函数，求出它的全部（或多个）可获得的邻居数值，并在目前的融合态中求出几个最优候选数值。

（d）对于在目前的融合状态中的候选者，判定在目前的融合状态中的通路是否比最初的通路S0小。如果该问题成立，那么将在初始态下的最优值x替换为在现有条件下满足蔑视标准的候补的最优状态值y，从而得到新的最优当前解，即x=y。在此基础上，将上一阶段中的“best so far”态的解决方案用上一阶段中的解决方案替代上一阶段中的解决方案，接着进行到第（6）步；反之，接着进行下面的操作。

（e）在目前的情况下，根据目前的情况，确定每一种被试的情况下所对应的所有被试的相同的禁制特性，并选取目前的融合状态候试的解集，以目前的不受试的被试的最好的状态，为新的融合状态下的解集。并且将原本在禁止列表中的所有被禁止的目标，都用相同的状态下所对应的目标代替。修订禁止使用的表格。

（f）在目前的情况下，对该融合解决方案是否符合最短路条件进行判定。如果是，那么在目前的情况下，该算法将立即终止，并且在融合后的运行中输出最优的结果；如果没有，那就回到第三步，然后重新开始。融合算法流程图如图4所示。

车辆停放过程中，车辆的横向移动和纵向移动必须同步进行，也就是本课题所讨论的车辆装载问题，多个车辆停放在同一泊位上。提出了在保证每个泊位的情况下，以最小的总运程为目标的原则[9]。根据这个推论，我们可以做出如下的假设：

（a）每个停车位的进出门和每个停车位的真实位置是知道的，每个停车位是空的还是满的。（b）对于每个分拣堆积器在进站和进站过程中的存放和取车的时间和泊车就位所需要的时间是没有任何考量的。（c）在一个运输期间，所有的堆叠器都以同样的速度，以同样的速度，以同样的方式前进，而不用担心电力供应的问题，确保了每个运输过程都能持续地进行。（d）在各存储位置上，各存储位置上的时间是相同的。（e）一次只能有一部车辆通过该通道。（f）无论车辆的型号或牌子，停车场的车位都是一样的，并且一个车位只能停靠一台满足进站要求的车辆。（g）当所述叠置器工作时，所述叠置器能够沿竖直提升和横向移动两个方向进行装卸动作[10]。

6 结语

本文研究立体车库存取车路径优化，选择单出入口巷道堆垛式立体车库作为研究对象，围绕着排队模型的建立及路径规划优化算法两个层面展开研究，论文的研究工作可以概括为以下几个方面。

（1）进行巷道堆垛式智能立体车库的总体测控方案设计。确定了排队论建模方式。完成了立体车库控制策略研究，包括立体车库衡量指标平均队长、平均排队长、平均等待时间与平均逗留时间的设定，立体车库布局的设置，确定了存车优先策略，确定了车位分配策略。完成了立体车库客流分布研究，建立了排队模型，完成了立体车库单出入口下多服务台排队模型分析。

（2）进行了常用路径优化算法研究，确定了基于Floyd算法和禁忌算法的融合算法作为立体车库路径优化算法，进行算法设计及软件编程调试，完成了路径优化后数据处理数据比对分析。

参考文献：

[1]韩艳，李婉莹，杨光，张甜甜.居住区停车场立体化改造决策机理[J].北京工业大学学报，2019，45（09）：879-885.

[2]周柳娜.立体车库智能控制系统研究[J].电子测试，2020（17）：26-27.

[3]臧赤丁，李广，吴杭.双模车牌识别系统探析[J].中国交通信息化，2019（03）：109-111.

[4]姚刚，吴斌，赵雪刚.机械式立体车库在既有住区改造中的应用[J].住宅科技，2019，39（07）：43-46.

[5]贺云鹏，李建国，张海飞.基于改进遗传算法的立体车库布局及配置优化[J].武汉大学学报（工学版），2020，53（05）：464-470.

[6]孟广耀，穆国振，王文涛，李正.新型立体车库设计及分析[J].中国工程机械学报，2019，17（04）：340-344.

[7]邱玉琢，张磊.碳排放规制下生鲜农产品配送车辆路径优化问题[J].南京财经大学学报，2021（01）：68-78.

[8]方景芳，袁冲.基于车间道路约束的物料配送模型及算法研究[J].电子设计工程，2020，28（23）：18-24.

[9]杨明.机械式立体车库的发展现状及实际运用分析[J].内燃机与配件，2020（15）：180-181.

[10]郭中旺，陈大宁，杨旭，贺涛涛，郭永灵，于周斐.智能立体车库设计[J].智能计算机与应用，2020，10（04）：199-202.