自锁式正四棱柱结构单元的构形参数研究＊

赵占伟 侯艳芳

（陕西工业职业技术学院，陕西 咸阳 712000）

折叠网架结构是一种临时性建筑结构体系，常应用在军事、救灾等场景中以解决人员和设备庇护问题[1]。因具备双稳态特性[2]，展开后可稳定地承力，折叠后可方便地运输和储纳。对于一般的折叠网架结构，由不稳定的展开状态转换成稳定的结构状态还需要施加额外的几何约束，而自锁式折叠网架结构则无须这样的约束，一旦展开成形便可直接稳定承载[3]。 “自锁” 对于自锁式折叠网架结构达成预期建筑功能尤为关键。因具备 “自锁” 性质，该类网架的展开和折叠也更加迅捷，可为军事行动及灾民等争取到宝贵的机动时间和救援契机。

自锁式结构单元是自锁式折叠网架结构的基本组成构件[4,5]，其中本文研究的正四棱柱结构单元随柱面式网架结构及平板式网架结构的应用而得到大量应用。然而在工程实践中，经常会发现不同构形的结构单元， “自锁” 能力迥异，甚至部分单元无法完成自锁。作为整体网架的锁定功能单元，若达不到合理的自锁能力，那么整体结构的实用价值也会大大降低。此外，相同空间外形条件下，相较于一般网架的结构单元，自锁式结构单元的制造需要更多的材料消耗，无论从组装成的整体网架受力能力方面还是从经济性方面看都是不利的。因此，要了解整体结构的自锁性能，需要从基本构成单元的自锁性能着手。

从设计层面看，通过构形设计方法可以数学表达自锁式结构单元的空间构形[6]。因此，单元的自锁能力与构形设计方法相关性极大。然而，同一构形结果可以使用不同的设计方法，每种方法则对应不同的构形参数。故，若探讨单元的自锁性能，还需基于一定的构形设计方法，通过对应的构形设计参数，开展系统研究。

1 构形参数

1.1 单元的构形特征

结构单元的组成功能部件是剪式单元[7]，其两根杆件通过枢轴相连接，并能够在垂直于枢轴轴线的平面内相互转动。多对剪式单元可组装成结构单元，赋予机构运动的能力。而满足建筑使用需求的完整网架结构，可最终由合适数量的结构单元组装完成。每个独立的结构单元均具备一定的自锁能力，且均可独立承担并传递建筑荷载，因此结构单元是该类网架结构的基本结构构件。

展开时正四棱柱结构单元的构形，如图1所示。因外形是由四个相同的外围平面（边杆剪式单元所在平面）围成，其空间几何形状为正四棱柱而得名。不同于一般网架的结构单元，正四棱柱结构单元的内部存在四个相同的辐杆剪式单元，是形成自锁能力的关键构造。

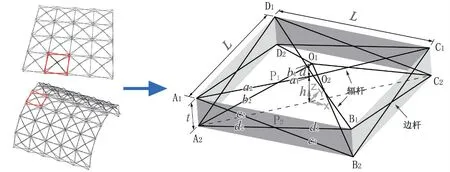
图1 正四棱柱结构单元的空间构形及其设计参数

1.2 单元的构形参数

正四棱柱结构单元的构形设计参数（见图1）。采用棱柱的上下底面边长L，间距t，结构单元的内部节点O2至底面A2B2C2D2的垂距h，O1O2的间距d共4 个量作为构形设计的基本参数。

①结构单元上下底面边长L。该值与整体折叠网架结构的纵向长度有关。

②结构单元上下底面间距t。该值的初步选取一般根据建筑需求及结构自锁能力选定。

③结构单元内部下节点到下底面的距离h。该值的初步选取也根据结构自锁能力及建筑需求而定。

④结构单元内部上、下节点的间距d。该值的选取需满足结构单元完全展开时的构形要求，即需满足下式：

其中，P1z是辐杆上的枢轴点P1至底面A2B2C2D2的垂距。

此外，P1点在辐杆上的位置还需满足结构单元完全折叠时的构形要求，即结构单元中的杆件必须满足可折叠条件：

式中a2、b2、c2、d2分别为相应剪式单元的杆件被其枢轴点划分的长度。

显然对折叠网架结构而言，可折叠条件是所有几何约束中最独特且十分关键的条件，也是求解参数值时的收敛判定条件。

构形设计时，间距t和边长L一般给定，p1z也可根据展开后的空间几何关系表达为关于参数d和h的函数。综合来看，由式(1)可知，d和h两个参数是相关的。因此，可以完整地描述结构单元空间构形的参数数量由原来的4个变为当前的3个。故，后文选择了L、t和h作为参数研究对象。

2 自锁能力评估及折叠中的截面内力

正四棱柱结构单元的 “自锁” 现象出现在展开阶段。但对于一般的结构单元而言，其展开过程与折叠过程互为可逆向的过程。从便于建模角度考虑，可通过折叠过程探究结构单元的 “自锁” 性能。利用有限元软件Abaqus 建立结构单元的折叠过程的数值分析模型。在参数L、t、h分别取为1500mm、300mm、240mm时，生成典型尺寸下的正四棱柱结构单元空间构形。模型中的杆件采用薄壁空心圆管，截面尺寸为16mm×1mm；铝合金材质，E为7.2×104MPa，G为2.7×104MPa，μ为0.3；采用B33 闭口梁单元。杆件之间采用不考虑节点尺寸的理想连接方式，即剪式单元间采用铰接连接；剪式单元内部两杆件只在枢轴处释放单元转动平面内的相对转动自由度，其余自由度上均相互约束。模型的边界条件设置为节点O2铰接于支座上，节点O1在正四棱柱结构单元的中心线上移动。

模拟的正四棱柱结构单元的折叠收纳过程，如图2所示。衡量结构单元自锁能力强弱的最直观方法就是通过折叠过程中所需的外力大小来判定。该组构形设计参数数据下得到的外荷载随上节点O1位移的变化曲线，如图3所示，其中节点受到的力向上为正。因在完全展开时没有弹性形变，故曲线的初始值为a 点的0值。b点为曲线的正向最大值点，只有提供的折叠力大于该力，结构单元才能够顺利折叠，故该值的大小表明了结构单元自锁能力的强弱。过c点后力变为反向，结构单元完成 “解锁” ，并且能够在撤除荷载后完成自动收拢。d点为曲线的负向最大值点，该值很大程度上决定了结构单元的自动收拢能力。至e点曲线重新回到0值，结构单元收拢完毕，此时杆件不存在弹性形变。由上述分析可知，b点值RF3b是判定结构单元自锁能力的指标。

图2 模拟的正四棱柱结构单元撤收过程

图3 正四棱柱结构单元荷载-位移曲线

由剪式单元的构造特点可知，枢轴处的内力应为最不利内力。因而，选取两种剪式单元的枢轴处的内力，给出模拟结果曲线，如图4所示。其中，轴向力（SF）以受拉为正，剪式单元的平面内弯矩（SM）以杆件上部受拉为正。此外，因剪式单元的平面外方向的弯矩很小，故无须绘制。可以看出，内力曲线的线形相同。折叠阶段前期内力快速增大到一个幅值，后期又较缓慢地减小至完全折叠收纳时的0值。

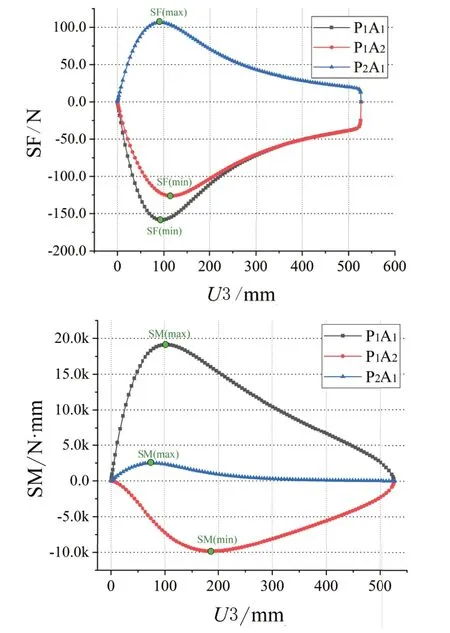
图4 正四棱柱结构单元内力-位移曲线

在SF图中，所有杆件都在位移100mm左右达到最大幅值，与RF3曲线c点出现的时刻吻合。表明这一时刻正四棱柱结构单元撤收过程中，所有杆件内部之间的几何不相容已经积累到最大。过了这一时刻，内部几何不相容逐步减小，内力也随之逐步减小。在该组构形设计参数下，折叠中所有杆段的轴向力水平基本相当，其中辐杆较大。然而，经计算可知，折叠中的绝大部分时段，杆段同一截面中的弯曲应力数值远大于同一时刻的轴向应力，超过一个数量级，即杆件的截面应力主要由弯矩产生。

在SM图中，可以推得辐杆的弯曲应力水平高于边杆很多。位移在100mm 左右时，所有杆段的综合弯曲弹性应变达到最大。而辐杆P1A1内的弯矩最高，几乎是另一根辐杆P1A2的三倍。位移过100mm 后，结构单元完成 “解锁” 。辐杆P1A1迅速释放应变，减小弯曲变形。随之，边杆剪式单元出现较大的整体向上位移的相对趋势，并减小了自身弯曲变形。边杆将辐杆P1A1的整体平移位移作用，最终通过A2节点的向上位移转作用到了辐杆P1A2上，导致其曲线反而持续下凹。随折叠过程推进，各杆段的空间角度持续变大，结构单元杆件内部之间的相对位移趋势情况也随之改变。在位移至200mm 左右时，所有杆段的综合弯曲应变达到解锁后的较大水平。此时，对应RF3 曲线d 点，正四棱柱结构单元具备最大折叠收拢能力。

3 构形参数对自锁及内力的影响

3.1 上下底面边长L

在t、h的值取为300mm、240mm 时，L选取800mm至2400mm 区间内每间隔200mm 的数值。建立系列数值折叠模型，来探讨该参数对正四棱柱结构单元自锁能力及折叠过程中的内力水平的影响。得到的结果，如图5所示。其中，内力图中的符号max 及min 表示的是在折叠过程中截面内力曲线在数值上的幅值（参照图4）。

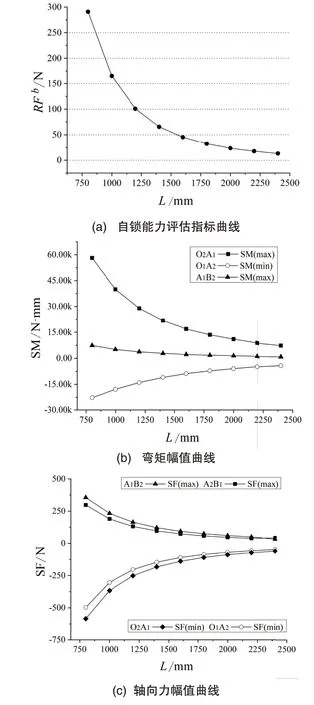
图5 自锁能力评估指标及内力幅值随参数L的变化图

可以看出，在参数t、h一定的情况下，不同杆段中内力幅值的相对大小关系没有变化，不受参数L的影响。自锁能力判定指标RF3b和截面内力，随L的变化特征均一致。三图中的曲线，先期均从边长L较小时的大值快速变小，后期在边长L无限大时变化缓慢且无限接近于0值。这说明，参数t、h的值选择合理时，不论结构单元外形宏观尺寸有多大，结构单元都将具备一定的自锁能力。

从内力曲线看，结构单元L的值越小，截面应力水平应越高，越容易超出线弹性下材料的强度要求。此外，从经济性以及结构承力的角度看，在保证相近的建筑使用空间要求的前提下，一般组成整体网架结构的单元数量越少，结构在单位体积上的质量也就越小。这也就要求初步设计时，L的值要尽量取得大一些。然而，考虑压弯构件的稳定性，L的值不宜选取的过大。结合工程经验，RF3b值在15N～90N之间为宜。因此，正四棱柱结构单元的L可在1263.3mm～2328.75mm 之间做初步选取。

3.2 上下底面间距t

因选取的参数数据范围过大对于结构单元的应用意义不大，因此这里选取的参数值是：设计参数L和h分别取为1500mm、240mm，t取为区间250mm～450mm内每间隔25mm的数据。系列数值模型结果，如图6所示。可看出，参数t与参数L的变化趋势一致，自锁能力判定指标RF3b和截面内力曲线均随t的增加而非线性地减小。内力曲线中，辐杆O2A1的内力水平依然是同时刻最高的，不同杆段的截面内力的相对大小也始终得以保持。正四棱柱结构单元的RF3b在15N～90N之间时，相应的上下底面间距t在260.24mm～391.2mm之间。

图6 自锁能力评估指标及内力幅值随参数t的变化图

3.3 单元内部下节点到下底面的距离

在设计参数L、t固定取为1500mm、300mm时，选取参数h在140mm～300mm 区间内间隔20mm 的数据，结果如图7所示。与前两个参数情况相反，RF3b和截面内力曲线反而随h的增大而增大。并且，h在140mm附近时，RF3b接近于0，正四棱柱结构单元失去自锁能力。在h的合理取值范围内，辐杆O2A1的截面内力依然大于其他杆件的弯矩。RF3b在15N～90N 之间时，对应的h值在189.7mm～269.2mm之间。

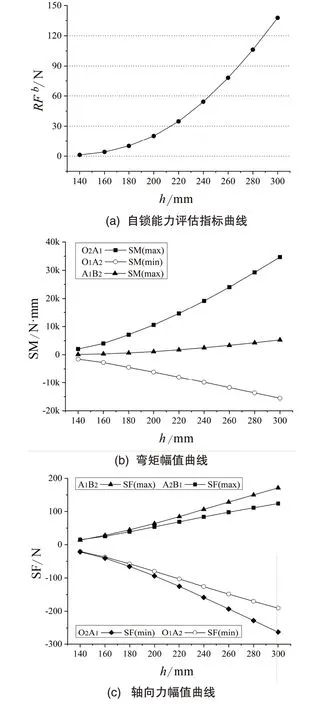
图7 自锁能力评估指标及内力幅值随参数h的变化图

4 结语

本文基于自锁式正四棱柱结构单元的构形设计原理，模拟分析了单元折叠撤收过程。探讨了参数对结构单元折叠、展开过程中的截面内力及自锁能力的影响问题。选取了三个构形设计参数作为研究对象，最终得到以下结论：

（1）折叠过程中的外荷载-位移曲线反映了正四棱柱结构单元的自锁性能。该曲线的最大正值的大小，可以评估单元自锁能力的强弱；最大负值的大小，可以评估单元自动折叠能力的强弱；中间0 值点，可以推定结构单元完成 “解锁” 的时刻，过该点后结构单元可自动折叠收纳。

（2）正四棱柱结构单元自锁能力主要取决于其杆件内的整体弯曲应变水平。因结构单元折叠过程中的弯曲应变远远大于轴向应变，故而 “解锁力” 主要由杆件的弯曲程度决定。

（3）随三个构形参数的增大，自锁能力及内力幅值曲线的变化趋势一致。二者均随着控制结构单元外形的两个参数值的增加而非线性地减小，而在另一个决定内部节点位置的参数情况中则呈相反变化。在结构设计时，可基于此变化特点调试参数，较快地得到满意结果。

（4）为方便正四棱柱结构单元设计参数值的初步选取，在杆件外径为16mm，壁厚为1mm，采用铝合金材质的前提下，基于一组基本构形参数值（L、t、h分别为1500mm、300mm、240mm）给出了L、t、h三个参数的合理 取 值 区 间：1263.3mm～2328.75mm，260.24mm～391.2mm及189.7mm～269.2mm。