运用“列表”或“画树状图”分析概率

文／江苏省南通中学附属实验学校 陆奕佳

生活中我们时常会遇到一些难以预料的事。随着认识的深入，我们发现，不同事情发生的可能性大小不同，一些事有可能发生，也有可能不发生。

一般地：当事件有n种可能性相同的结果，而事件A包含其中的m种结果，则事件A发生的概率。从这个公式中我们不难看出P（A）的取值范围是0≤P（A）≤1。特别地：当A为必然事件时，P（A）=1；当A为不可能事件时，P（A）=0。

了解概率后，遇到具体的问题，我们还可以选择列表法或画树状图法来分析并计算概率。

例1同时掷两枚质地均匀的骰子，计算下列事件发生的概率。

（1）事件A：两枚骰子的点数相同；

（2）事件B：两枚骰子点数之和为8。

解：两枚骰子分别记为“a”和“b”，列表列举结果。

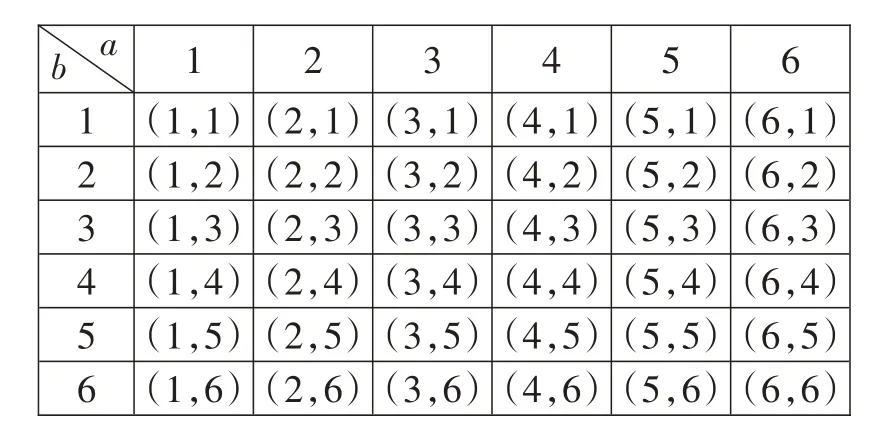
从上表可知：同时掷两枚骰子共有36 种结果，并且它们发生的可能性相等。可得，。

例2经过某十字路口的汽车由于前方施工只能左转或右转。假设这两种可能性大小相同，求三辆汽车经过该十字路口时，两车右转一车左转的概率。

解：设三辆汽车分别为A、B、C，画树状图如下：

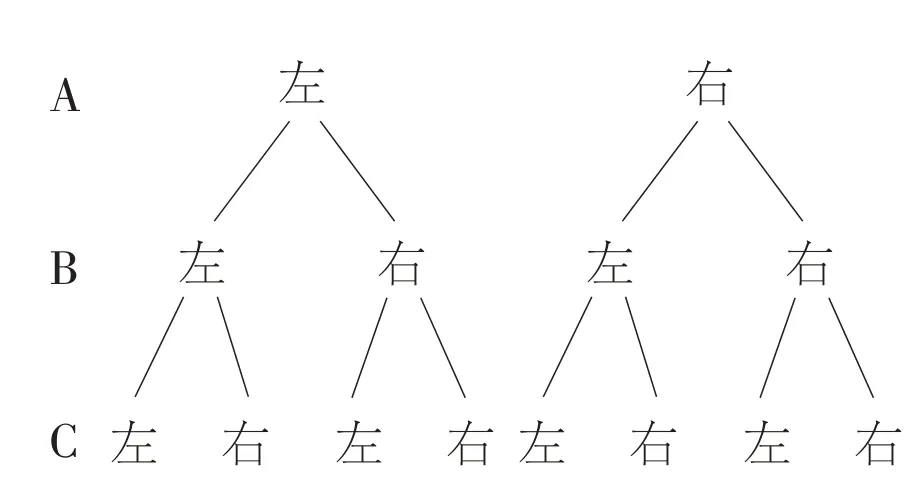
由图可知：共有8 种可能性相同的结果，而两车右转一车左转对应其中的3 种。所以P（两车右转一车左转）=。

教师点评

陆奕佳同学从对事件发生的可能性的大小开始，引入概率的概念，阐述了对概率的认识，总结了概率的求解方法，充分体现了对数学知识的单元建构。文章中所列举的例题都是生活中的具体问题，体现了数学来源于生活，又服务于生活的特点。