无人机协同定位防欺骗的WGAN-TM识别方法

魏杨沁, 郭 庆, 许 洁, 张 鹏, 邹金霖

(空军工程大学装备管理与无人机工程学院,西安 710000)

0 引言

近年来,随着计算机和控制理论的迅猛发展,无人机技术也不断取得进步,与此同时,反无人机的手段也层出不穷。其中,较为典型的是通过伪造虚假的定位信号,攻击GPS等卫星接收设备,使得编队中的无人机解算出错误的位置信息。为应对此类欺骗干扰,确保无人机编队正常执行任务,常用方法是从信号着手,在物理层面对比真实和伪造信号的特性,或者对信号进行加解密认证以识别真伪,此类方法的局限性在于只能事先预防,不能解决无人机实时因欺骗干扰导致的位置偏移的问题。另一种方法则是从无人机定位状态的异常检测着手,常见算法主要可以分为2大类:一类是基于标签的异常检测算法,另一类是基于模型的异常检测算法。其中,基于标签的异常检测算法又可以细分为3种:一是无监督异常检测算法,该算法通过寻找相比其他数据最不匹配的实例对测试数据异常进行标记;二是监督式异常检测算法,该算法需要事先准备“正常”和“异常”标签数据集;三是半监督异常检测算法,该算法根据所给定的正常训练数据集创建一个表示正常行为的模型,随后对由学习模型生成测试实例的可能性进行检测。基于模型的异常检测算法主要包括基于统计的算法、基于重构的算法(例如PCA)、聚类分析(例如K-means)、one-class算法(例如OC-SVM、SVDD)等。

随着人工智能技术的广泛运用,基于深度学习的异常检测算法成为新热点,该算法利用深度神经网络对传统基于模型的检测算法进行改进,例如Deep clustering、Deep one-class、Autoencoder、Generative models等。基于深度学习的检测算法中最为广泛的是长短时记忆网络(LSTM)检测算法,李晨等[1]在用LSTM数据预测的基础上,将实际值与时序预测值偏差输入分类器进行训练,提高了检测的准确性;黄勇等[2]将模糊神经网络与专家系统结合,提高了无人机故障检测的效率。上述算法存在的一大不足在于需要技术人员在训练中提供大量的异常样本。近年来,随着生成对抗网络(GAN)的提出,部分学者开始尝试利用GAN进行飞行数据异常检测,GAN的一大优势在于无需事先收集大量异常数据进行训练。王凤芹等[3]通过将GAN与LSTM组成循环网络,构建正常飞行数据模式,对处于离线状态的无人机进行异常检测。上述异常检测算法只能应对系统总体异常,而无法甄别系统中具体异常的个体(单个或多个)。当检测到无人机编队遭到欺骗后,接下来需要解决的问题就是区分异常无人机与未遭到欺骗的正常无人机。假设整个编队都是信息透明的“白盒”,每架无人机的数据都能通过观测准确实时获取,这种区分就显而易见。而在实际应用中,难以直接通过观察实时掌握无人机各项数据,这样的编队就应视为“黑盒”,此时,无论是否被欺骗,无人机都会认为自己按照“正确”的航线飞行,因此会向编队或地面站报告自己的位置是“正常”的,而此时某些无人机实际则出现了异常。因而单凭编队中各机所报告的信息,难以判断哪些无人机遭到了欺骗。针对这样的问题,一种可行的解决方式是采用虚拟结构法(Virtual Leader),设置一个虚拟点作为编队的虚拟长机,编队中各无人机需要确保和这个虚拟点的相对位置不变以维持编队队形。通过这种方法,只要有无人机报告的相对距离出现异常,就可判断该机遭到了欺骗。另一种方式是实时对无人机航迹坐标进行预测,通过比较无人机的航迹预测值与无人机自身的GPS接收机定位值之间的差异,就能快速判断无人机是否被欺骗,如孙旸等[4]基于长短时记忆网络建立轨迹预测模型,判断无人机是否遭受欺骗干扰,并利用卡尔曼滤波器提高了预测精度。

1 无人机编队定位防欺骗问题

为了提高作战任务的成功概率,无人机常采用编队协同的飞行模式,尤其是在侦察、打击目标等方面,编队飞行的无人机可以大大提高任务效率。对无人机而言,在空中能否准确定位,对能否顺利执行任务有极其重要的作用。从公开的文献可以看出,当前对于无人机定位进行欺骗的手段层出不穷,其中比较常用的是GPS欺骗,这种手段通过伪造GPS信号,使得无人机解算出错误的位置信息,从而达到欺骗的目的。尤其当编队中某架无人机定位遭到欺骗,将对整个编队的作战效能产生不利影响。本文运用WGAN网络对编队是否遭受欺骗进行整体上的检测,随后在无人机间通过建立信任模型判断遭受欺骗无人机的(单架或多架)具体编号[5]。

1.1 生成对抗网络(GAN)

GAN是一种典型的无监督学习算法,最早于2014年由GOODFELLOW等基于博弈论中的双人零和博弈问题提出[6]。GAN由生成模型和对抗模型组成,其中,生成模型的作用在于通过生成与训练数据相近的数据以图混淆判别器,其输入是n维服从某种概率分布的随机噪声,输出为生成样本;判别模型的作用在于对来自生成模型的样本和真实数据进行判断,以真实样本或生成样本为输入,以当前样本为真的判别概率为输出。通过训练GAN即可得到较为灵敏的系统异常检测系统。

1.2 Wasserstein生成对抗网络(WGAN)

GAN通过生成模型与判别模型之间的博弈,不断提高生成器和判别器效能。自GAN问世以来,在异常检测、图像生成、模式识别等多领域取得了广泛的应用,但传统的GAN存在着诸如训练不稳定、模式崩溃等问题。针对于此,文献[7]提出了一种利用Wasserstein距离代替GAN生成器中使用的JS散度和KL散度的方法,对传统GAN进行了改进。Wasserstein距离定义为

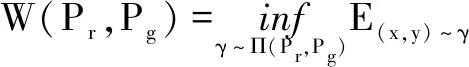
(1)

式中:Π(Pr,Pg)为Pr,Pg的联合分布,对于任一个联合分布γ而言,可以从中采样得到一个真实样本x和生成样本y,计算得到样本距离为‖x-y‖;进一步可得到期望值E(x,y)～γ(‖x-y‖)。在所有期望值中取下界,这个下界就被定义为Wasserstein距离[8]。相比于GAN使用的JS散度和KL散度,Wasserstein距离的优势在于能平滑地反映真实样本与生成样本之间距离的大小,即使这两个分布之间未产生重叠。

基于此,WGAN在原始的GAN上做出的改进主要体现在:

1) 去除判别器最后一层的Sigmoid函数;

2) 生成器和判别器的损失不作取对数处理;

3) 判别器参数每轮更新后进行截断处理,使其不超过一个固定常数a;

4) 不再采用GAN中常见的基于动量的优化算法(momentum和Adam),而是采取RMSProp进行优化。

1.3 信任模型

信任模型最初来自于网络安全领域,其研究始于信任管理这一概念。参考实际的人际关系网络,人对于他人的信任度有两种,一种是自己对这个人的了解和认识,还有一种方式就是参考其他人对于这个人的评价和认识。与之相对应的,信任度可以划分为直接信任度与间接信任度两种。通过在无人机编队各机间建立直接信任度和间接信任度模型,进一步可以综合获得各机的综合信任值,进而得以对编队内遭受欺骗的具体无人机进行准确识别。

2 基于WGAN-TM的无人机协同定位防欺骗识别方法

2.1 模型总体结构

基于WGAN-TM的无人机协同定位防欺骗识别方法模型总体结构如图1所示。

图1 模型总体结构

整个模型由WGAN训练模型、异常检测模型和对欺骗进行识别的信任模型3个部分组成,异常检测模型输入为测试样本,利用WGAN训练模型中训练好的生成-对抗网络,根据得到的价值函数判断编队是否出现异常。如果判断为异常,则根据编队各机间的信任度模型,比较各无人机的信任度,从而判断出编队中出现异常的无人机的精确编号。

2.2 WGAN训练模型结构

WGAN训练模型由生成器(Generator)与判别器(Discriminator)构成。如图2所示。

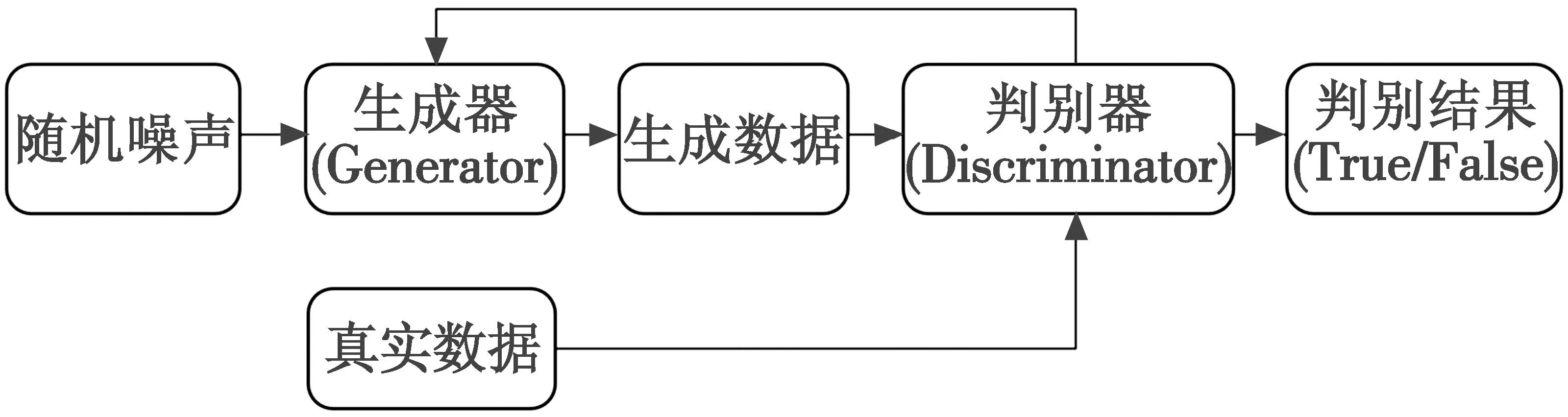
图2 WGAN训练模型结构

WGAN训练过程包括判别器训练和生成器训练两部分。生成器以随机生成的噪声作为输入,其目标是生成尽可能“真实”的数据用于欺骗判别器;判别器则以真实数据和噪声数据为输入,尽可能判别出真实数据与生成器的伪造数据[9]。整个WGAN运行的过程即是判别器与生成器的博弈过程,这样最终得到的WGAN,其生成器将具备较强的伪造数据能力,而判别器也将灵敏地对数据真实性进行判断。WGAN器的一轮训练过程如下所述。

1) 固定生成器,训练判别器。从原始训练集中选出真实样本x(真实性标签为1)作为判别器输入,判别器输出的判别概率记为D(x)。将判别概率与真实性标签对比可得到损失LD,1,判别器损失LD算式为

LD=Ex～Pg[D(x)]-Ex～Pr[D(x)]

(2)

式中:x～Pg表示x是对真实样本Pg的采样;E为期望值;x～Pr表示x采样自生成样本Pr。

将随机噪声输入生成器,得到生成样本(真实性标签为0),将生成样本输入判别器,得到判别概率,记为D(G(z)),将判别概率与真实性标签对比,可得到损失LD,2。然后,计算判别器损失,并将损失反向传播到判别器的各个节点中,并更新网络参数,判别器一轮训练完成。

2) 固定判别器,训练生成器。将随机噪声z输入至生成器,得到生成样本G(z),将生成样本作为判别器输入,得到判别概率D(G(z)),将其与真实性标签对比得到损失LG,1,生成器损失LG算式为

LG=-Ex～Pg[D(x)]。

(3)

将损失反向传播到生成器的各个节点,并更新网络参数,生成器一轮训练完成。由于生成器的目的是尽可能使判别器将生成样本判断为真实样本,因此通常要将生成器输出的真实性标签设置为1,让生成样本向真实样本靠拢。

生成器与判别器在不断博弈过程中得到优化,设WGAN整体的价值函数(即优化目标)为

goal(G,D)=Ex～Pg(D(x))+Ez～pz(z)(D(G(z)))

(4)

式中,z～pz(z)表示z采样自噪声分布pz(z)。

2.3 欺骗识别信任模型

经异常检测后,可初步判断为编队遭受欺骗干扰,但具体欺骗发生于哪架(或几架)无人机还不可知,需要进一步识别。而事实上欺骗难以被精准描述,根据经验,可以从欺骗的对立面——信任——去描述,如果协同单元中的无人机不被信任,则表示其被欺骗的可能性变大。此时,可对无人机协同定位的信任模型进行解算,以支撑欺骗的识别。各机间的信任值可以分为直接信任值和间接信任值。

2.3.1 直接信任值

编队中,某无人机对其他无人机的直接信任值,是由该无人机自身观测的位置与其他无人机根据结合观测及机间相对位置关系得到的该无人机位置之间关系决定。例如,t时刻无人机i根据自身设备测得坐标为(xii,yii),而无人机j根据其观测得到的两机间位置关系算得无人机i坐标为(xij,yij)。对无人机i而言,如果(xii,yii)与(xij,yij)坐标是重合的,则无人机i对无人机j的信任度为1。据此可认为无人机i对无人机j的直接信任值满足

tij=e-[(xii-xij)2+(yii-yij)2]i≠j

(5)

信任值取值范围设为(0,1)。

2.3.2 间接信任值

无人机i对无人机j的间接信任值,是由编队中其他无人机k(即第三方)与无人机j的信任关系决定。显然,对于无人机i而言,要得出对无人机j较为合理的判断,还需要综合其他无人机对无人机j的评价(即第三方评价)。设无人机i对无人机j的间接信任值为t′ij,其算式为

(6)

式中:αk为无人机k的性能权重,它与无人机k的抗欺骗能力、测算精度等有关;tkj为无人机k的间接信任值。

进一步可得到无人机j在编队中的间接信任值T′j,它体现了无人机j根据自身设备观测的其他无人机的位置信息在编队各机间的认可度,即

T′j=∑t′ij。

(7)

2.3.3 综合信任值

在编队内,无人机i对无人机j的综合信任值,是由无人机i对无人机j的直接信任值与间接信任值加权获得。当无人机i自身的抗干扰定位能力强于编队内其他无人机时,其直接信任值的权重更高;当编队内其他无人机的抗干扰定位能力优于无人机i时,可认为其他无人机对无人机j的评价权威性要高于无人机i对无人机j的评价,即间接信任值的权重更高。权重的具体大小可以利用信息熵理论计算。直接信任值tij的熵函数H(tij)为

H(tij)=-tijlb(tij)-(1-tij)lb(1-tij)

(8)

进一步可得直接信任值tij对应的熵权为

(9)

间接信任值t′ij的熵函数H(t′ij)和熵权w′ij采取同样方法计算。综合信任值由直接信任值与间接信任值加权获得,综合信任值的权重qij为

(10)

根据文献[9]的算式,得到综合信任值为

Tij=qijtij+(1-qij)t′ij。

(11)

2.3.4 基于总信任值的判断

当获取到无人机i对无人机j的综合信任值后,进一步可以得到编队各机对无人机j的总信任值为

(12)

分析总信任值数据中的异常值,即可精准判断出具体受欺骗的无人机,从而实现欺骗的精准识别。

3 实验结果和分析

3.1 实验数据处理

假设由100架无人机组成一个10×10的编队,编队各机位置分布如图3所示。

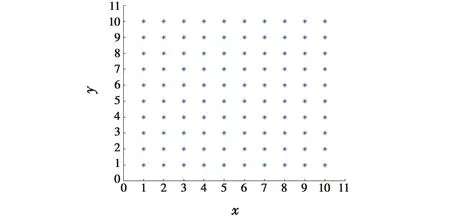
图3 编队各机位置关系

以该编队作为训练数据样本,输入WGAN进行训练。各迭代周期内生成器和判别器的损失如图4所示。

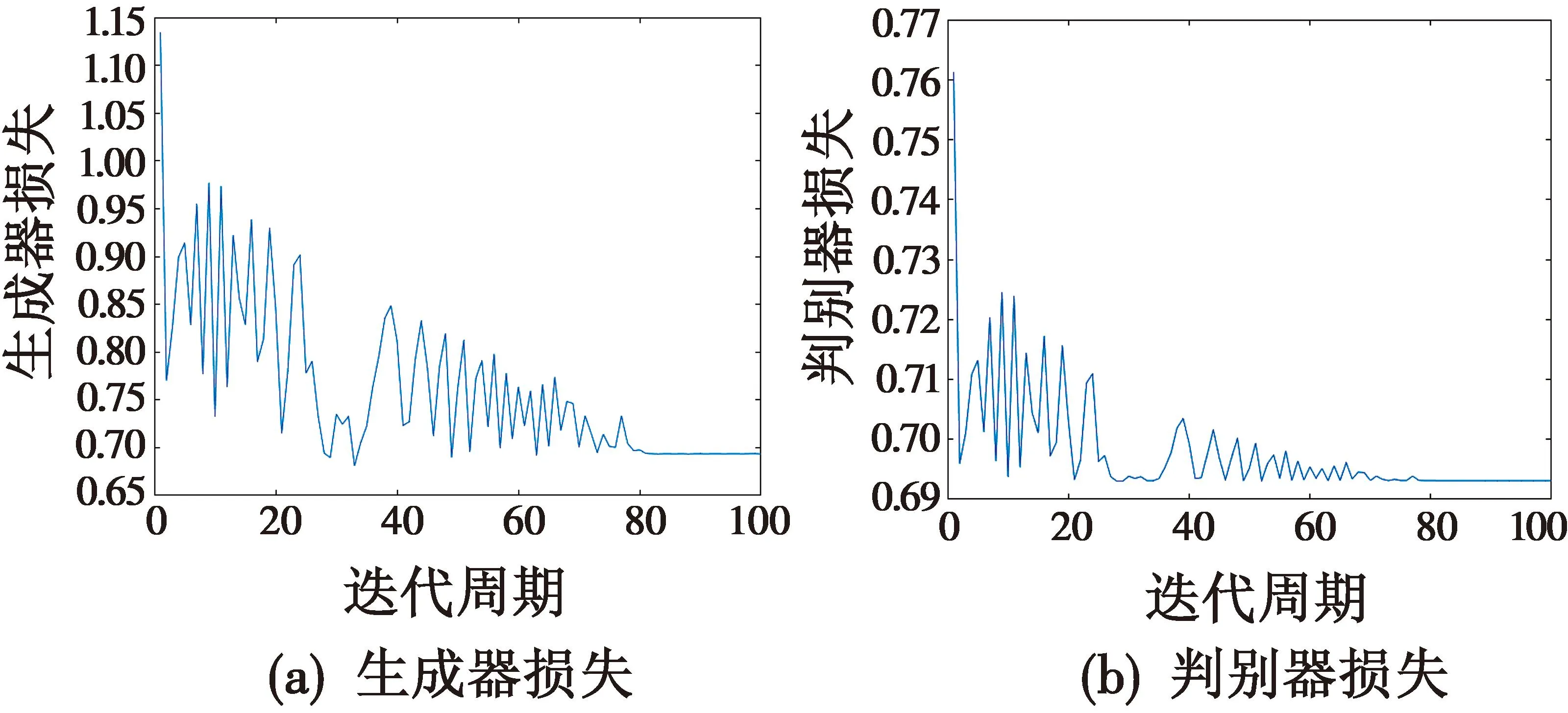
图4 生成器及判别器损失

由图4可以看出,随着迭代周期的增加,生成器的性能和判别器的性能都得到了明显提升,其损失值逐渐降低,这表明WAGN的检测效能在与生成器的博弈中不断得到改善。

为了检验WGAN检测效能,随机打乱其中10架无人机的位置,以此方法获得的100组编队位置分布图作为测试数据。其中一组遭受GPS欺骗后的无人机编队各机分布如图5所示。

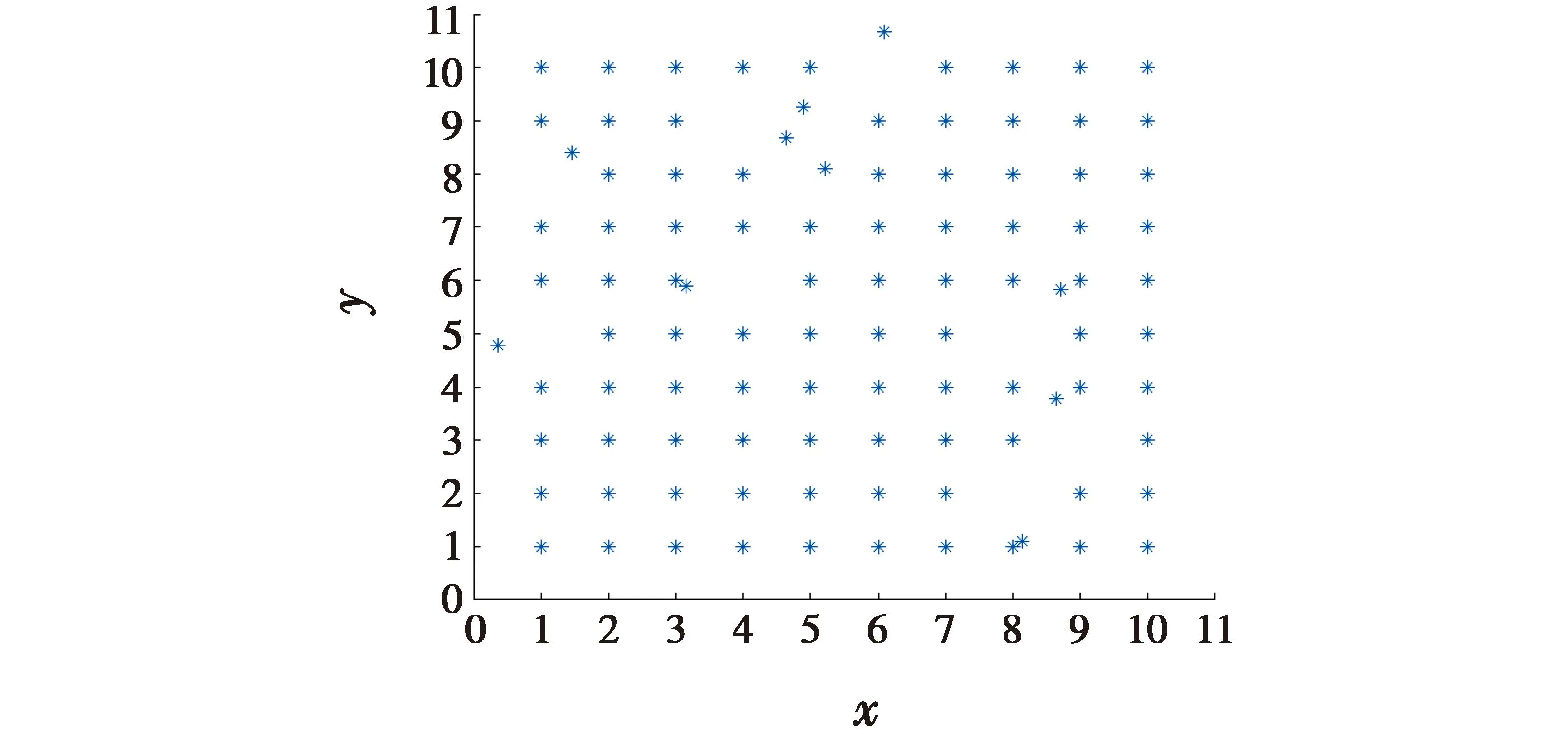
图5 遭受欺骗后的无人机编队

为了方便判断,将坐标为(1,1)的无人机编号为1,坐标为(1,2)的无人机编号为2,以此类推坐标为(10,10)的无人机编号为100。从图5可以直观地看出遭受欺骗的无人机编号为5、8、36、39、48、49、60、72、75、83。如果整个编队的信息都是透明的,就可以迅速通过上述方法找到具体遭受欺骗的无人机。但实际应用中往往只能获得各架无人机根据其自身设备所得到的信息,因此需要建立各无人机的信任模型,通过比较综合信任值进行判断。

3.2 模型效能评价指标

为了评价WGAN网络的GPS欺骗检测效能,引入真阳率RTP、假阳率RFP、精确率P及F1值作为评价指标。其中:RTP是衡量WGAN正确检测出编队遭欺骗的能力指标;RFP是衡量WGAN将正常状态的编队错误判断为遭到欺骗的指标;P代表检测为异常,实际也为异常的编队占检测为异常的编队数的比例。P和RTP的值都与模型效能正相关,但是两者存在制约关系,RTP越高则P越低,F1值的作用就是平衡P和RTP之间的关系。

(13)

(14)

(15)

(16)

其中:TP代表WGAN判断为异常实际也为异常的编队数;FP代表WGAN判断为异常实际为正常的编队数;FN代表WGAN判断为正常实际为异常的编队数;TN代表WGAN判断为正常实际也为正常的编队数。

3.3 实验过程与结果分析

由于本文研究的问题存在两个步骤:

1) 基于WGAN的编队欺骗问题检测;

2) 精准识别遭欺骗的具体无人机。

因此,实验结果分析也分为两个部分:

1) 评估WGAN的检测效能,基于相同的训练、测试数据,与LSTM、GAN、K-means聚类算法的性能进行对比;

2) 基于信任模型做出决策,对决策准确性进行评估。

以图5所示编队为例,根据前文建立的编队信任模型,得到当前编队各机直接信任值、间接信任值、综合信任值如图6所示。

图6 直接、间接及综合信任值

图6(a)中,曲线代表不同的无人机对该机的直接信任值,通过观察可以发现,曲线在编号为5、8、36、39、45、60、72、75、83这9架无人机处出现了突变。这说明这9架无人机报告的自己的坐标对于其他无人机来说可信度不高。

由图6(b)比较间接信任值可以判断,编号为5、8、31、36、39、48、60、72、75、83的无人机经过观测所报告的其他无人机的位置在编队各机间认可度不高,但要较为准确地判定编队内遭受欺骗的无人机,需要对直接信任值和间接信任值进行综合计算。

根据图6(c)综合信任值进行排序可知,编号为5、8、24、36、39、48、60、72、75、83的无人机总信任值相对其他无人机较低,这些异常表明这些编号的无人机所报告的位置信息可信度相比于编队中其他无人机较低,说明这些无人机有很大可能遭到了GPS欺骗。将信任模型得到的结果与图3编队位置信息对比可得信任模型的RTP为90%,RFP为1%,P为90%,F1值为90%。24号无人机被编队错误判断为异常机可能是由于其本身性能较差等因素导致在编队各机间评价的权重较低;而异常的49号无人机没有被编队判断出来,原因可能是因为它性能比较好,在编队里比较有“权威”,从而“成功”骗过了编队里的其他无人机。对100组编队的判断结果取平均值可得信任模型判断的RTP为91.4%,RFP为0.86%,P为90.3%,F1值为90.8%。可以看出,信任模型能比较准确地判断出编队内遭到欺骗的具体无人机编号。

3.4 算法对比分析

为验证本文算法的检测效果,在采用与3.1节中相同的编队数据基础上,分别使用GAN-TM、LSTM以及K-means这3种算法对编队无人机遭欺骗情况进行检测,利用3.2节采用的评价指标对各算法的检测性能进行比较,实验结果如表1所示。

表1 不同算法的编队欺骗检测性能对比

从表1可知,本文算法的欺骗检测综合性能要优于GAN-TM算法和K-means算法,也略优于LSTM算法。本文算法的RTP比GAN-TM、LSTM、K-means算法分别提高了1.7、0.8和6.1个百分点。对于检测的精确率P,本文算法比GAN-TM、K-means、LSTM算法分别提高了3.6、1.9、7.1个百分点。对于F1值,本文算法则比GAN-TM、LSTM、K-means算法分别提高了2.6、1.3和6.6个百分点。而对于RFP,本文算法相对GAN-TM和K-means算法分别降低了0.34和1.54个百分点,相对LSTM,则只高了0.14个百分点。相比于原始的GAN-TM算法,本文算法提高了训练的稳定性,同时在实际操作中,训练也更加容易。

4 结束语

本文将WGAN应用于无人机编队GPS欺骗检测,设计了生成器与判别器,通过生成模型不断与判别模型的博弈,提高了编队欺骗检测的精度,并在检测的基础上,在编队各无人机间建立信任模型,对具体遭受干扰的无人机作了识别。实验结果表明,本文所提出的基于WGAN的编队GPS欺骗检测算法的性能较好,同时对具体的遭欺骗无人机的识别较为准确。另一方面,由于WGAN还没有解决GAN存在的解释性较差、收敛速度慢等缺点,实际应用中可能会对系统的检测效率造成不利影响,未来还需要研究如何提高模型的检测效率。此外,还可以从改进信任模型这方面入手,进一步提高检测的准确度。