基于改进ADC法的侦察无人机作战效能评估

刘登攀, 寇昆湖, 王 超, 鹿珂珂

(海军航空大学,山东 烟台 264000)

0 引言

过去,无人机在战场上主要充当辅助角色,执行战场支援等作战任务。随着新材料、新技术的不断发展,无人机的发展也日新月异,逐渐升级成为能够执行侦察监视、打击、空中加油、通信中继等作战任务的新质作战力量[1]。侦察无人机系统作为战场上执行侦察监视、情报搜集、目标跟踪、为武器系统提供目指信息等任务的无人作战平台,在近几年的若干地区冲突中,发挥了越来越重要的作用[2]。作为未来无人化作战的重要平台,如何科学评估侦察无人机系统的作战效能,对于提高作战任务完成率非常关键[3]。因此,亟需一种科学、有效的评估方法对侦察无人机系统进行效能评估。

近年来,针对武器装备系统的效能评估研究取得了较多成果。文献[4]基于系统效能分析法(System Effectiveness Analysis,SEA)对反导预警系统进行作战效能评估,并结合仿真试验验证了该模型;文献[5]结合层次分析法和灰色评估法对装甲合成营装备体系作战效能进行评估,减小了评估过程中的主观性,使评估结果更加客观有效;文献[6-10]基于可用性-可信性-能力(Availability-Dependability-Capability,ADC)法对各类武器的系统效能进行评估,并通过算例验证了该模型的适用性和准确性。随着近年来人工智能等学科的不断发展,基于神经网络[11-13]、向量机[14-15]等方法也应用到了效能评估中。

通过对现有的典型评估算法进行比较,本文基于ADC法对侦察无人机系统进行作战效能评估,该方法简单可靠、逻辑性强,对无人机这种复杂系统进行作战效能评估具有十分重大的意义[16]。但传统的ADC法更多适用于无人机本身的系统效能评估,不适合直接用于无人机系统的作战效能评估。本文充分考虑无人机系统在实际作战时的人员保障因素和对抗因素,在传统ADC模型的基础上,引入保障因子S和战场环境因子H,提出改进型ADC评估模型。同时,结合层次分析法和模糊综合评判,对侦察无人机系统作战效能进行评估,旨在保证作战效能评估的完整性和严谨性。

1 改进ADC模型分析

ADC法是1963年美国工业界武器系统效能咨询委员会(WSEIAC)在其提出的系统效能定义的基础上建立的系统效能评估模型[17],其表现形式为

E=A·D·C。

(1)

对于侦察无人机系统来说,E为无人机的综合效能;A为系统可用性指标,表示无人机系统在执行任务前所处的所有可能状态;D为系统可靠性指标,表示无人机系统在执行任务期间状态转换概率;C为无人机系统的作战能力指标,表征无人机在某状态下完成侦察任务的能力。

考虑实际作战时人员保障指标S和战场环境指标H,将其融入传统的ADC模型中进行改进,改进后其表现形式为

E=A·D·C·S·H。

(2)

1.1 侦察无人机系统主要作战任务及作战过程分析

侦察无人机主要利用自身携带的光电、红外、雷达等任务载荷对某一战场的局部范围执行侦察监视等任务,为指挥员提供及时、准确的战场情报。

如图1所示,侦察无人机的主要作战过程可分为3个阶段:1) 战前准备阶段,是指在接收到作战指挥中心下达的作战任务后,对侦察无人机系统的上电、检查、准备、任务规划、装订航线阶段;2) 平台出航阶段,是指侦察无人机系统领受作战任务后向任务区域飞行的阶段;3) 执行任务阶段,是指侦察无人机系统到达任务区域后利用携带的任务载荷对当前区域实施侦察、搜索、识别、上报阶段。

图1 侦察无人机作战过程

1.2 侦察无人机效能指标体系建立

基于侦察无人机的作战任务和作战过程分析,结合改进的ADC模型,通过研究无人机执行侦察任务过程中的指标因素与作战能力指标之间的作用机理,梳理总结出侦察无人机作战效能指标体系。构建的侦察无人机作战效能指标体系划分为4个层次,如图2所示。

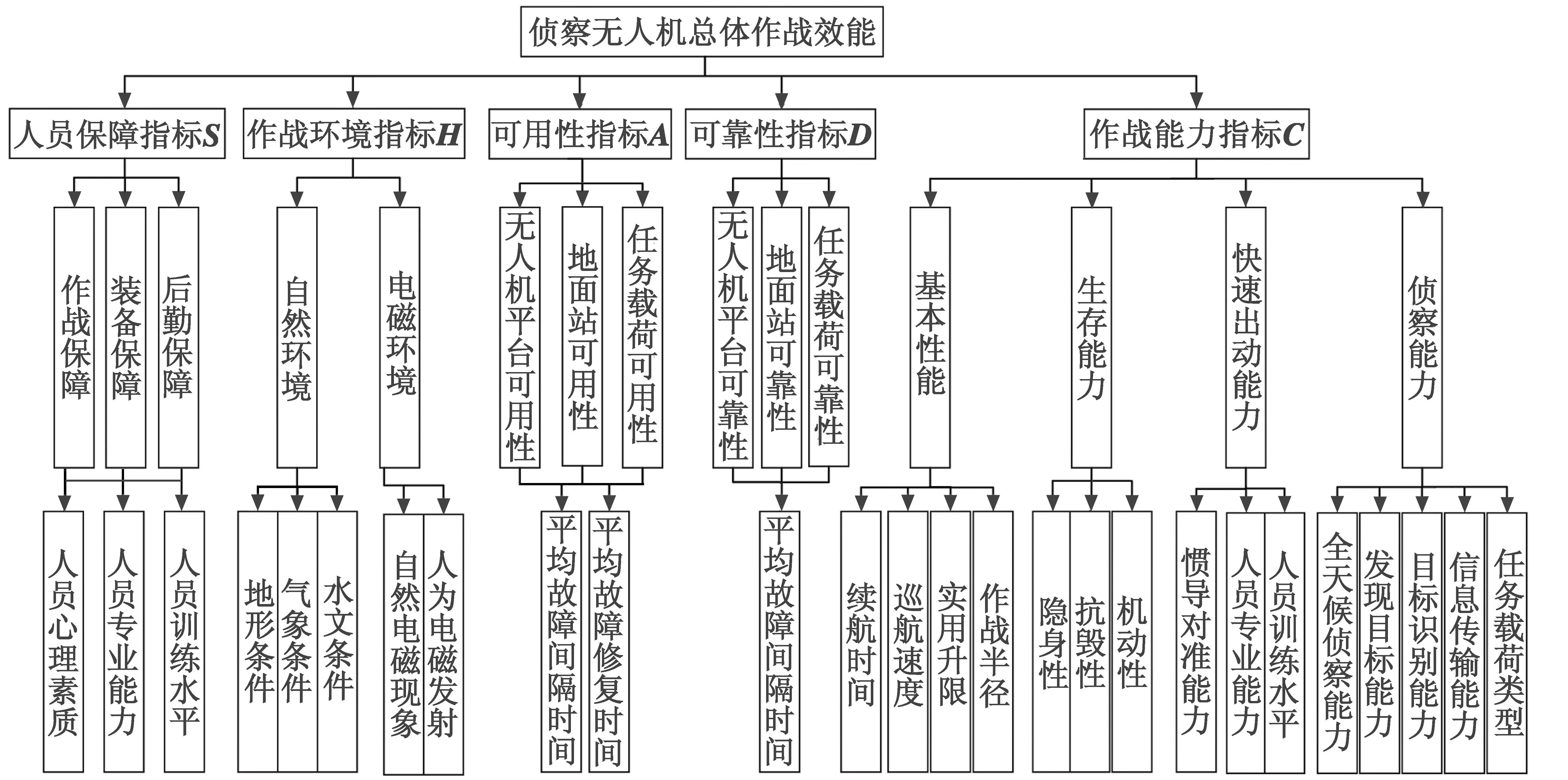
图2 侦察无人机作战效能指标体系

1.3 可用性指标A分析

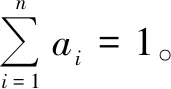
无人机系统中的每一种设备都有“正常”及“故障”两种状态(“故障”状态下,无人机仍具备执行侦察任务的能力,但作战效能有所降低,本文设定若一个子系统故障,任务能力削弱20%,2个子系统故障,任务能力削弱40%,3个子系统故障,任务能力削弱80%)。对于侦察无人机系统来说,一般分为飞行器平台、动力装置、电气系统、导航飞控系统、任务载荷系统、地面控制系统、保障设备等,若全面分析各个设备状态,则侦察无人机系统共有27=128种状态。为简化分析,可以分为无人机、地面系统、任务载荷系统3部分。设无人机为子系统1,地面系统为系统2,任务载荷系统为子系统3。根据以上分析,可以将无人机系统的初始状态划分如下:

1) 状态1 子系统1、子系统2、子系统3均正常工作;

2) 状态2 子系统1正常工作,子系统2正常工作,子系统3故障;

3) 状态3 子系统1正常工作,子系统3正常工作,子系统2故障;

4) 状态4 子系统2正常工作,子系统3正常工作,子系统1故障;

5) 状态5 子系统1正常工作,子系统2故障,子系统3故障;

6) 状态6 子系统2正常工作,子系统1故障,子系统3故障;

7) 状态7 子系统3正常工作,子系统1故障,子系统2故障;

8) 状态8 子系统1、子系统2、子系统3均故障。

上述初始状态划分如表1所示。

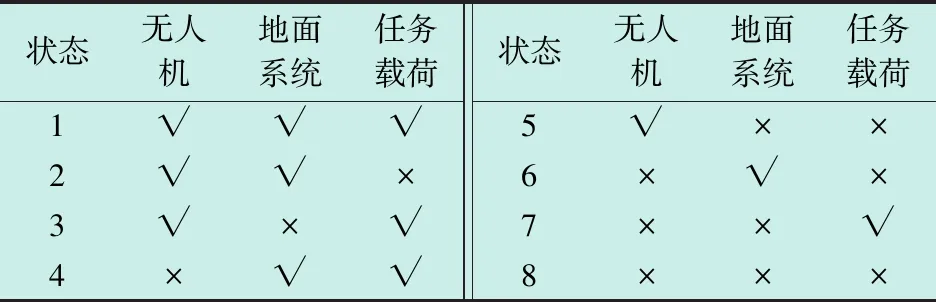
表1 无人机系统初始状态

分别用b1、b2、b3表示子系统1正常工作的概率、子系统2正常工作的概率、子系统3正常工作的概率。

无人机可用性指标指无人机系统各设备正常工作概率,可使用飞机平均故障间隔时间(MTBF)和平均故障修复时间(MTTR)近似表示为

(3)

式中:TMTBF,i为无人机各子系统的平均故障间隔时间;TMTTR,i为各子系统平均故障修复时间,具体数值参考MTBF取值。

则无人机系统各个初始状态的概率可以表示为

(4)

需要开始执行侦察任务时,无人机系统的可用性指标为

A=[a1,a2,a3,a4,a5,a6,a7,a8]。

(5)

1.4 可靠性指标D分析

可靠性指标D表示无人机系统在执行任务期间的状态转换概率。

由式(5)知,无人机系统在开始执行任务时有8种可能的状态,在任务初始阶段无人机可能处于任何一种状态。在理论上无人机在执行任务过程中可能由1种状态转化为其他7种状态,也就是说无人机系统有8种状态转化可能,因此可靠性指标D可表示为

(6)

式中,dij为在执行任务过程中,无人机系统由第i状态转移到第j状态的状态转移概率,且矩阵各元素之和为1。

无人机系统在任务开始之后,处于故障状态的设备不能维修,属于不可修复的装备系统。因此,如果在任务开始阶段无人机的某一子系统处于故障状态,那么在执行任务过程中该子系统将一直处于故障状态,不会转化为正常状态。

因此可靠性指标D可表示为

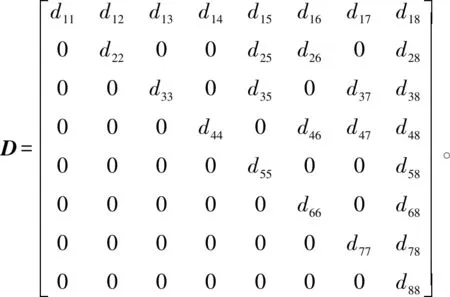
(7)

可靠性指标与侦察无人机平均故障间隔时间(MTBF)紧密相关。各子系统故障率λ与MTBF的关系为

(8)

假设无人机各子系统在执行任务过程中的MTBF服从指数分布,则可靠性(该子系统保持正常状态的概率)可表示为

P=exp(-(T/TMTBF))=exp(-λT)

(9)

式中,T为无人机飞行时间。

设子系统1故障率、可靠性分别为λ1、P1,子系统2故障率、可靠性分别为λ2、P2,子系统3故障率、可靠性分别为λ3、P3,则无人机系统在执行任务过程中由状态1转化为其他状态的概率为

(10)

状态2转化为其他状态的概率为

(11)

状态3转化为其他状态的概率为

(12)

状态4转化为其他状态的概率为

(13)

状态5转化为其他状态的概率为

(14)

状态6转化为其他状态的概率为

(15)

状态7转化为其他状态的概率为

(16)

状态8转化为其他状态的概率为

(17)

1.5 系统作战能力指标C分析

无人机系统作战能力指标表示无人机系统在8个不同状态下的作战能力,如图3所示。

图3 作战能力指标

侦察无人机系统作战能力主要由其基本性能、生存能力、快速出动能力以及侦察能力决定,即无人机完成侦察任务需要具备的能力。针对不同类型的指标采用不同的计算方式。

1) 对于定量类指标,其数值进行归一化处理[18],算式为

(18)

式中:C′为归一化后的数值;ci为指标当前数值,cmax为该指标可取的最大值;cmin为该指标可取的最小值。

2) 对于生存能力、快速出动能力以及侦察能力等定性类指标,本文结合层次分析法和模糊综合评判法[19]得到,从而求取不同状态下的C。具体步骤为:

① 通过专家打分,构造判断矩阵,确定其对应的权重系数;

② 根据图3所示的侦察无人机效能评估体系确立模糊评判的因素集U;

③ 建立指标的评语等级论域V并赋值,即V={优,良,中,差}={0.9,0.8,0.6,0.4};

④ 通过专家打分建立单因素评判模糊关系矩阵R;

⑤ 选取合适模糊算子,得到综合评价结果B;

⑥ 综合分析得到该能力的最终得分B·V。

1.5.1 基本性能C1

侦察无人机系统基本性能主要由续航能力、巡航速度、实用升限和作战半径等量纲类指标决定,各指标权重w1=[w11,w12,w13,w14]由层次分析法计算得到,采用效用函数法进行归一化计算得到各指标数值,基本性能模型为

(19)

1.5.2 生存能力C2

生存能力主要考虑无人机的隐身性、抗毁性和机动性,各子指标权重w2=[w21,w22,w23]和数值结合层次分析法和模糊综合评判法得到,采用加权求和确定生存能力模型。

1.5.3 快速出动能力C3

无人机的快速出动能力是指在领受作战任务后,无人机从系统组装、上电、检查、惯导初始对准到无人机起飞执行任务的时间,主要考虑操作人员专业能力和人员训练水平,同时受到惯导对准能力的制约,(惯导初始对准能力与其性能以及对准方式等密切相关)。各指标权重w3=[w31,w32,w33]由层次分析法计算得到,人员专业能力及人员训练水平数值采用Delphi专家评估法[20]得到;惯导对准能力通过对其惯导对准时间进行规范化处理得到,通过加权求和确定最终模型

(20)

式中:T为该型无人机的惯导对准时间;Tmax为惯导对准时间可取的最大值;Tmin为可取的最小值。与续航能力、巡航速度等效益型指标不同的是,惯导对准时间属于成本型指标,因此采用不同的规范化方法。

1.5.4 侦察能力C4

无人机的侦察能力主要考虑全天候侦察能力、发现目标能力、识别目标能力、信息传输能力和任务载荷类型,各指标权重w4=[w41,w42,w43,w44,w45]由数值结合层次分析法和模糊综合评判法得到,其中当侦察无人机同时具有可见光侦察、雷达侦察、光电侦察时,任务载荷类型该项指标得分定为0.9,同时具备雷达侦察和光电侦察时,该项指标得分定为0.8,只具有光电侦察能力时,该项指标得分定为0.7。最后通过加权求和确定侦察能力最终得分。

1.5.5 作战能力计算

分别确定侦察无人机的基本性能、生存能力、快速出动能力和侦察能力权重,结合前文计算的各指标得分得到最终作战能力得分。

1.6 保障指标S分析

本文考虑作战人员的保障因素在侦察无人机作战效能发挥中的作用。保障指标主要包括作战保障Szz,装备保障Szb,后勤保障Shq。作战保障主要包括侦察情报、通信、机要交通、航空管制等方面的保障;后勤保障主要涉及经费供应、医疗救护以及生活需要等方面的保障;装备保障主要是指装备分配、装备维修等方面进行的保障。各类保障工作主要受人员心理素质、人员训练水平及人员专业能力的影响。不同的使用人员、不同的使用方式对应着不同的保障水平,进而影响无人机作战效能发挥。依据图2已建好的指标体系,利用层次分析法求出作战保障、装备保障、后勤保障3个指标及其子指标的权重。利用Delphi专家评估法得到末端指标数值,最后采用加权求和法得到保障能力值。

(21)

式中:wzzi、wzbi、whqi分别为作战保障、装备保障和后勤保障中作战人员心理素质、训练水平、专业能力所占比重;Si(i=1,2,3)分别表示作战人员心理素质、训练水平、专业能力得分;P为专家打分的平均分(0～100),Pmax=100为满分。wi分别表示各子指标权重。

1.7 作战环境指标H分析

作战环境是影响侦察无人机作战效能的重要因素之一,主要考虑自然环境及电磁环境,包括地形、气象、水文以及敌方电子干扰等环境条件。各级指标权重由层次分析法计算得到,指标数值通过专家咨询打分获得。

2 算例验证

为验证该模型的有效性,应用上述改进ADC模型进行仿真实验验证。

2.1 可用性指标A计算

假定该无人机及各子系统的平均故障间隔时间、平均故障修复时间如表2所示。

表2 平均故障间隔时间和平均故障修复时间

由表2中数据及式(3)、式(4)可计算出无人机系统的可用性指标

A=[0.8699 0.0580 0.0290 0.0373 0.0019 0.0025 0.0012 0.0002]。

2.2 可靠性指标D计算

假定该无人机每次出航执行任务的时间为10 h,即T=10,则由式(8)～(17)可得无人机各子系统在执行任务过程中可靠度向量

D=

(22)

2.3 作战能力指标C计算

2.3.1 基本性能计算

1) 用层次分析法确定各指标权重。

作战能力指标判断矩阵如表3所示。

表3 判断矩阵

根据表3判断矩阵解得权重系数为w1=[0.3564,0.1242,0.3257,0.1936],一致性比率CR=0.0293<0.1,一致性检验通过。

2) 归一化处理指标数值。

利用式(18)对量纲指标进行归一化处理,结果如表4所示。

表4 基本性能指标归一化处理

3) 加权求和确定基本性能得分。

结合权重系数及归一化后的数值,得到基本性能得分为0.377。

2.3.2 生存能力计算

1) 层次分析法确定各指标权重。

此处步骤不再赘述,得到的生存能力末端指标的权重系数为w2=[0.5584,0.1220,0.3196],CR<0.1,满足一致性要求。

2) 模糊综合评判确定各指标数值。

通过邀请专家打分评判,得到生存能力评判数据如表5所示。

表5 生存能力指标评判数据

模糊综合评价结果B=w2R=[0.1543,0.5575,0.2001,0.0881]。

3) 加权求和确定生存能力得分。

最终得到该无人机生存能力得分为C2=B·V=0.7373。

2.3.3 快速出动能力计算

首先,利用层次分析法确定各指标权重系数为w3=[0.4,0.4,0.2],利用专家评估法得到人员专业能力和人员训练水平得分为[0.85,0.90],利用该无人机的惯导对准时间和式(20),得到该无人机的惯导对准能力值为0.4,加权求和得到快速出动能力最终得分为0.78。

2.3.4 侦察能力计算

首先通过AHP确定侦察能力末端指标权重系数为w4=[0.0972,0.4185,0.2625,0.1600,0.0618],根据前文所述,该无人机任务载荷类型指标得分为0.8,其他4个末端指标数值由模糊综合评判得到,则最终侦察能力得分为0.8018。

2.3.5 作战能力计算

通过层次分析法确定第一级指标权重W=[0.1278,0.2391,0.0930,0.5401],CR=0.05<0.1,满足一致性要求。

结合前文计算出的基本性能得分C1、生存能力得分C2、快速出动能力得分C3和侦察能力得分C4,通过加权求和得到分系统全部正常情况下的作战能力为0.7301。

根据1.5节分析,可得到不同状态下的无人机系统作战能力指标为C=[0.7301,0.5841,0.5841,0.5841,0.4417,0.4417,0.4417,0.1460]。

2.4 保障指标S计算

2.5 作战环境系数H计算

作战环境系数计算与2.4节保障系数计算类似,在此不再赘述计算步骤,直接给出计算结果。通过Delphi专家打分得到地形、气象、水文自然环境得分为[0.65,0.85,0.55],自然电磁现象和人为电磁发射等电磁环境得分为[0.85,0.90],自然环境各级权重通过AHP得到wzr=[0.1349,0.7838,0.0813],电磁环境各级权重为wdc=[0.42,0.58],作战环境各级权重为whj=[0.35,0.65],CR值均小于0.1,满足一致性检验。

通过加权求和确定最终作战环境得分为0.8509。

2.6 效能计算

综合以上分析,无人机的综合效能E=A·D·C·S·H=0.4601,若不考虑人员保障因素和作战环境因素则获得的作战效能得分为0.63。从最终的效能结果来看,改进后的ADC法在综合考虑保障因素和作战环境因素后,得到的侦察无人机系统的作战效能相比传统的ADC法较低。这是因为改进后ADC法将侦察无人机系统置于较为真实的战场环境,并考虑到人为因素对作战效能的影响,更加贴近实战。

3 结论

本文根据侦察无人机的实际作战任务和作战过程,对传统的ADC模型加以拓展改进,并在指标分析中综合利用层次分析法和模糊综合评判法,计算逻辑清晰,最后通过算例验证了该方法的有效性。

本文所提出的改进型ADC法,能够得到比较科学的判据,能够有效地对侦察无人机系统作战效能进行科学评估,能够为后续其他武器系统效能评估提供有益参考,具有较好的应用价值。