关于图形变换中的折叠探究
孙锴


[摘 要] 折叠是图形变换的一种方式,图形折叠中涉及了点、线段、图形的一些特殊性质,是几何综合题构建的基础. 中考综合题中常见几何折叠,探究问题特征,总结解题策略就显得十分有必要. 文章挖掘几何折叠的本质,归纳解题策略,探究矩形背下的几何折叠问题.
[关键词] 图形;折叠;线段;模型;矩形
问题综述
折叠是几何变换的一种方式,以其为背景构建的几何问题在中考中十分常见,问题设计新颖,变化多样,能够全面考查学生的读图与分析能力.
几何中的折叠问题,本质上就是对称问题,图形折叠中隐含着全等,对应边、对应角相等. 实际考查时常从综合视角切入,涉及三角形全等及相似、四边形的性质定理、勾股定理等知识,同时隐含了数形结合、分类讨论、方程、模型构造等数学思想. 探究解析需要立足折叠特性,把握知识关联、合理使用几何的方法技巧来构建思路.
关于几何折叠问题,解题突破有如下三种策略,可根据题型特点灵活选用.
策略1:根据图形折叠的知识本质,折叠前后所得的两个图形全等,对应点的连线被对称轴垂直平分,可利用其几何特性来构建模型;
策略2:提取问题中的特殊模型和特殊关系,如直角三角形、三角形相似等,灵活运用勾股定理、相似三角形的性质来构建线段关系;
策略3:把握知识关联,结合问题中的相关图形性质,如圆的性质、四边形性质等,将问题转化为特殊的几何问题.
问题探究
几何折叠问题的类型较多,图形结构丰富多变,图形的构建背景不唯一,常见的有矩形、三角形、一般四边形等. 设问涉及线段关系、动点轨迹、分类讨论模型等多种形式,下面结合实例探究矩形背景中的折叠问题,总结方法.
1. 矩形折叠与线段比值
矩形折叠中的线段比值问题,即以矩形为背景构建几何折叠,探寻其中的线段比值关系. 探究解析的核心是转化构建图形中的线段关系,可提取其中的特殊模型,利用勾股定理、三角形相似的性质来转化构建.
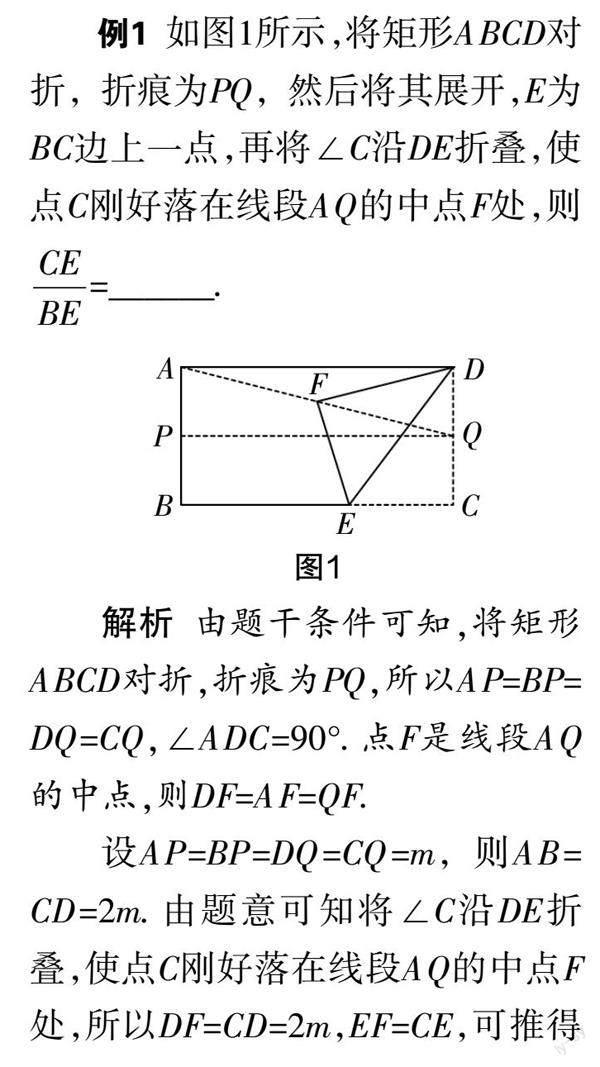
解析 由题干条件可知,将矩形ABCD对折,折痕为PQ,所以AP=BP=DQ=CQ,∠ADC=90°. 点F是线段AQ的中点,则DF=AF=QF.
设AP=BP=DQ=CQ=m,则AB=CD=2m. 由题意可知将∠C沿DE折叠,使点C刚好落在线段AQ的中点F处,所以DF=CD=2m,EF=CE,可推得DF=AF=QF=2m,设EF=CE=n.
解后评析 上述为矩形折叠中的线段比值问题,考查了轴对称、矩形、勾股定理、直角三角形斜边中线等相关知识. 解题的关键是把握折叠过程,合理构建模型,提取其中的特殊三角形,利用勾股定理来构建线段关系,将线段比值问题转化为与线段参数相关的代数问题进行分析.
2. 矩形折叠与模型讨论
矩形折叠与模型讨论问题,即以矩形为背景构建动态问题,解析时需要讨论其中的模型,如点位置模型、图形形状模型等. 问题解析需要关注其中的动态要素,设定条件,分类构建模型,针对模型开展讨论分析.
例2?摇 如图3,在矩形ABCD中,已知AB=10,AD=6,动点P从点D出发,以每秒2个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,把△ADP沿着AP翻折得到△AEP. 作射线PE与边AB交于点Q,当QE=QB时,t=______.
解析 本题目以矩形为背景构建了动点移动以及三角形折叠. 问题分析等线段情形下动点的移动时间,需要讨论点E的位置,分别构建几何模型讨论.
情形1:当点E在矩形ABCD的内部时,如图4所示. 四边形ABCD为矩形,则AB∥CD,∠APD=∠BAP. 题目中将△ADP沿着AP翻折得到△AEP,其中AD=6,由折叠特性可推得∠APD=∠APE,∠D=∠AEP=90°,AD=AE=6,DP=EP=2t,所以∠BAP=∠APE,∠AEQ=90°,从而有QA=QP=PE+QE=2t+QE.
情形2:当点E在矩形ABCD的外部时,如图5所示. 可推知∠APQ=∠APD=∠PAQ,所以AQ=PQ. 因为QE=PE-PQ=DP-PQ=2t-PQ=QB,所以BQ=2t-AQ=AB-AQ,则AB=2t=10,可解得t=5秒.
解后评析 上述探究等线段条件下移动时间t的值时,采用了数形结合、分类讨论的方法. 基于动点E的位置来分别构建模型,充分利用图形折叠的相关知识,把握其等线段、等角条件展开推导. 整个过程全面考查了几何相关知识,涉及矩形的性质、几何动点、折叠的性质、勾股定理的应用、等腰三角形的性质等知识.
3. 矩形折叠中的路径与面积
矩形折叠中的路径与面积,即以矩形折叠为背景,探究其中动点的运动路径,以及由此生成的关联图形的面积. 问题解析依然需要从图形折叠出发,分析折叠前后点、线、图形之间的关联,再确定其中的动点轨迹,构建最值模型求解.
例3?摇 如图6所示,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则三角形AGC的面积的最小值为______.
解析 本题目中以矩形折叠为背景,探究三角形的面积最小值,属于几何动态面积问题. 问题解析需要关注图形折叠后的位置,分析动点的移动范围,再构建模型开展面积最值分析.
解后評析 上述探究几何折叠背景中的图形面积最值时,把握图形折叠过程,确定点的位置关系,进而构建最值模型求解. 问题解析的关键有两点,一是解析折叠,确定点的相关位置关系;二是转化面积问题,构建△ACG面积最值与点G的位置.
4. 矩形折叠与坐标函数
矩形折叠与坐标函数,即在坐标系中分析矩形折叠,坐标系中的几何折叠具有了“数”的特性,可结合函数曲线推导点坐标,利用点坐标求解线段长. 对于折叠中的几何特性,可从几何、代数两大视角来进行突破.
解析 上述问题中将矩形折叠与坐标系相结合,求解反比例函数特征参数的值. 解析时要充分利用折叠特性来推导线段长,充分利用相似特性及勾股定理构建线段关系,解方程求k值.
解后评析 上述探究坐标系中的矩形折叠,折叠过程中的线段长、点位置具有了“数”的特性,于是问题解析时可利用函数解析式来求点坐标. 对于问题中的线段推导,可以利用相似三角形的性质及勾股定理,另外还可以利用正切值求反比例函数图象上点的坐标特征.
教学建议
上述探究了矩形背景中的折叠问题,深入挖掘了问题知识背景及破解策略,并结合实例探究了四类常见题型. 下面结合教学实践,提出几点建议.
建议1:透视几何折叠,挖掘折叠本质
图形折叠是几何运动的方式之一,开展几何折叠探究教学,要引导学生透视折叠,深刻理解折叠. 因此,教学中要挖掘其知识本质,可从两大视角进行:一是全等视角,即折叠前后的图形为全等关系,如三角形全等;二是对称视角,即图形关于折痕对称,且对应点的连线段被折痕平分. 教学时要引导学生思考,结合图形进行论证. 可采用如下两种方式:一是设问引导,结合矩形折叠的常见问题,让学生口述折叠过程,提起其中的几何性质;二是拓展引导,引导学生思考折叠中的知识关联.
建议2:总结归纳问题,形成解题策略
上述探究了矩形折叠常见的四类问题,涉及了线段比值、模型讨论、路径与面积以及坐标函数. 问题形式虽多样,但其解题方法及构建思路具有一定的关联性,解题探究时要注意总结归纳,生成相应的解题策略. 如提取问题中的特殊图形和特殊关系,基于全等、相似来构建线段关系. 处理折叠中的面积问题时,基于割补法将其转化为特殊图形的面积. 教学中教师要指导学生强化训练,积累经验,生成解题策略.

