以核心素养为导向 拓展探究型创新题

邴国良 银英

2024年辽宁省中考数学样卷的压轴题（第23题）被调整为几何综合探究题，这与辽宁省各市历年中考压轴题相比变化较大.此题是几何综合题中拓展探究型的创新题，其设置体现了以核心素养为导向，由解题走向解决问题的数学学科考试测评方向，通过问题初探、类比分析、学以致用考查考生分析问题、解决问题的能力.

原题再现

【问题初探】

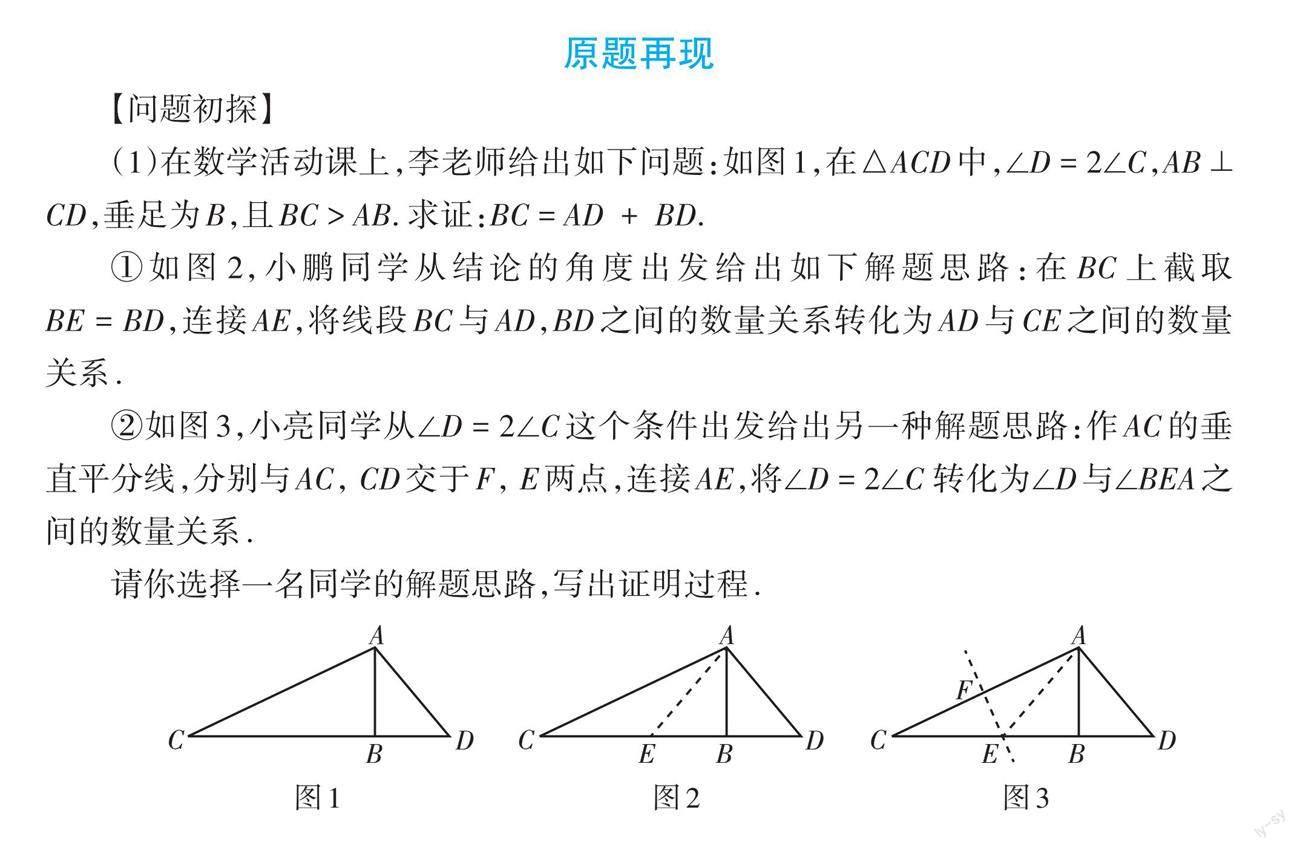
（1）在数学活动课上，李老师给出如下问题：如图1，在△ACD中，∠D = 2∠C，AB ⊥ CD，垂足为B，且BC > AB. 求证：BC = AD  +  BD.

①如图2，小鹏同学从结论的角度出发给出如下解题思路：在BC上截取[BE=BD]，连接AE，将线段BC与AD，BD之间的数量关系转化为AD与CE之间的数量关系.

②如图3，小亮同学从∠D = 2∠C这个条件出发给出另一种解题思路：作AC的垂直平分线，分别与AC， CD交于F， E两点，连接AE，将∠D = 2∠C 转化为∠D与∠BEA之间的数量关系.

请你选择一名同学的解题思路，写出证明过程.

【类比分析】

（2）李老师发现之前两名同学都运用了转化思想，将证明三条线段的关系转化为证明两条线段的关系. 为了帮助学生更好地感悟转化思想，李老师将图1进行变换并提出了下面问题，请你解答.

如图4，在Rt△ABC中，∠ABC = 90° ，过点A作AD [?] BC（点D与点C在AB同侧），若∠ADB = 2∠C. 求证： BC = AD + BD.

【学以致用】

（3）如图5，在四边形 ABCD中，[AD=1003]，[CD=1213]，[sinD=35]，[∠BCD=∠BAD]，∠ABC = 3∠ADC，求四边形 ABCD 的面积.

破解策略

第（1）题：需具备的知识储备有等腰三角形的性质、三角形外角的性质、垂直平分线的性质或三角形全等的判定.本小题相当于给出了部分范例，需要同学们补充详细证明过程，也为后续的类比分析与学以致用提供了证明的主要转化方向：一个是转化线段之间的关系，另一个是转化角度之间的关系（二倍角的转化）.

方向1：线段转化——截长补短

思路：如图2，在BC上截取BE = BD，连接AE，可得AB所在直线为线段DE的垂直平分线，则AE = AD，可得∠D = ∠AEB. 由∠D = 2∠C，得∠AEB = 2∠C，进而可得∠C = ∠CAE，则CE = AE = AD，所以BC = AD + BD.

方向2：二倍角转化——利用外角和等腰三角形转化

思路：如图3，作AC的垂直平分线，分别与AC，CD交于F，E两点，连接AE，则AE = CE，易证∠BEA = 2∠C. 由∠D = 2∠C，得∠D = ∠BEA，则AE = AD，BE = BD，所以BC = AD + BD.

第（2）题：在第（1）题的基础上增加了“AD [?] BC（点D与点C在AB同侧）”而且“∠ADB = 2∠C”，考生需要思考：“添加的这两个条件起什么作用？”进而思考：“通过怎样的转化会出现问题1中的基本图形？”思考方向还是线段截长补短和二倍角转化.

思路1：如图6，在BC上截取BE = AD，连接AE，证[△ABE≌△BAD]，转化为问题（1）.

思路2：如图7，作AC的垂直平分线，交BC于点E，证[△ABE≌△BAD]，转化为问题（1）.

思路3：二倍角减半，如图8，延长AD至E，使DE = DB，连接BE，交AC于F，证[△ABE≌△BAC]，转化为问题1.

思路4：二倍角减半，从结论出发，结合一边一角造等腰，如图9，延长BD至H，使DH = AD，连接AH，作∠CBG = ∠C，点G在AC上，易证[△BAH≌△BGC]，则BC = BH = BD + DH = BD + AD.

第（3）题：这是本道压轴题的难点，是求不规则四边形的面积，而条件分别从边和角给出.解答时要将已给图形与前两题中的基本图形比较，思考：是否需要添加适当的辅助线（一般情况下都要添加）将其转化为基本图形？是否需要分类讨论？图形不完整时，怎样正确做出需要补充的图形？模仿不是照搬，大体方向一致即可（例如，全等有可能变成相似）.需有的知识储备：三角函数知识，分析问题、解决问题能力及画图能力.

第一步：梳理条件，找到切入点——先标注条件，再寻找简化条件的方法.

如图10，延长线段AB，DC交于点E，

设∠ADC = α，[∠BCD=∠BAD] = β，

则∠ABC = 3∠ADC = 3α.

在△AED中，∠E = 180° - （α + β）①，

在四边形ABCD中，α + 3α + β + β = 360°，

∴2α + β = 180°②，

由①②可知∠E = 2α + β - （α + β） = α.

∵∠ABC = 3∠ADC = 3α，∠ABC = ∠E + ∠BCE，

∴∠BCE = 2α.

如图11，过点A作[AF⊥CD]于F，

在△AFD中，由[sin D=35]，可得AF = 20，EF = FD = [803]，CF = [413]，CE = 13.

至此，同学们会发现四边形ABCD的面积等于△AED的面积与△BEC的面积之差.解决问题的关键是求△BEC的面积.

第二步：回归基本图形，应用已证结论快速求解.

如图12，作BH ⊥ CE于點H，由前面已知CE = 13，△BEC为第（1）题中已证模型，可得EH = BC + HC，设BH = 3x，BE = 5x，EH = 4x，则HC = 13 - 4x，BC = 8x - 13.

在△BHC中，由勾股定理可得（[3x]）2 + （13 - 4[x]）2 = （8[x] - 13）2，解得x = [10439]，所以BH = 3x = [10413]，∴四边形ABCD 的面积 = [12·DE·AF-12·CE·BH=12×1603×20-12×13×10413=14443].

拓展延伸

（1）问题情境：如图13，正方形ABCD中，AB = 6，点E为射线BC上一动点，将△ABE沿AE所在直线翻折，得到△AFE，延长EF，射线EF与射线CD交于点G，连接AG．

①当点E在线段BC上时，求证：DG = FG；

②当CE = 3时，则CG的长为_______.

（2）思维深化：在△ABC中∠BAC = 45°，AD为BC边上的高，且BD = [2] + 1，CD = [2] - 1，请直接写出AD的长．

答案：（1）①略；②4或[365]. （2）AD的长为[2+3]或[1].

（作者单位：沈阳市南昌初级中学，沈阳理工大学附属学校）