具有Markov 切换脉冲随机时滞系统的有限时间稳定
尹 浩 ,姚凤麒 ,王国庆
(安徽工业大学 电气与信息工程学院, 安徽 马鞍山 243032)
随机噪声扰动在实际工程系统中是不可避免的,当系统的可靠性要求较高时,随机噪声扰动不可忽略。脉冲跳变可刻画系统状态在某些时刻的突变或重置,如电力网络中开关电路的频繁改变、生物种群系统中对生物的过度捕捞或投放等。脉冲随机系统综合考虑了随机噪声扰动和脉冲跳变两因素对系统的影响。时滞也会影响系统的性能,作为一类重要的混杂系统,脉冲随机系统得到了广泛研究。对于大多系统,脉冲发生的时间间隔不是均匀分布的,因此难以准确判断脉冲区间的长度。Lu 等[1]首次提出了平均脉冲区间的概念,允许脉冲区间的上确界可能非常大,而下确界可能相当小。Yao 等[2]利用平均脉冲区间方法,结合比较引理和Razumikhin技巧,建立考虑系统的矩指数稳定性的充分条件;Cai 等[3]利用Lyapunov 函数法和Razumikhin 技巧,建立了具有时滞脉冲离散时间不确定脉冲神经网络的鲁棒指数稳定;Wu 等[4]利用平均脉冲区间方法,建立脉冲随机时变系统的渐近稳定性的充分条件;Xu 等[5]建立了具有无限时滞的脉冲随机微分系统的矩指数稳定性的充分条件。
然而,上述研究成果多是基于Lyapunov 意义下的稳定性与控制,较少涉及系统的有限时间稳定。Lyapunov 稳定性描述系统在无穷区间上的渐进行为反映系统的稳态性能,但不能反映系统的暂态性能。Lyapunov 渐进稳定的系统具有较差的暂态特性,如超调过大等在实际系统中一般是不允许的。导弹系统、机器人操作系统等工作时间短暂,人们更关心的是系统是否满足一定的暂态性能要求。为解决系统的暂态性能问题,俄罗斯研究者Kamenkov[6]在20 世纪50 年代首次提出有限时间稳定的概念。有限时间稳定,是指系统初始状态在某一范围内时,系统的状态在一定时间区间内不超过某一预先给定的界限。近年,系统的有限时间稳定性问题再次引起广泛关注,并报道了系列研究成果[7-11]。Markov跳跃系统作为一类特殊的混杂系统,其中具有Markov 切换随机系统的有限时间稳定问题是热门的研究方向之一。Liu 等[12]研究了离散时间正Markov 跳跃系统的随机有限时间稳定性和镇定问题;Cheng 等[13]针对一类具有外部干扰和非线性的Markov 跳跃系统,提出了有限时间异步输出反馈控制方案;Ren 等[14]针对一类具有不完全转移率的Markov 跳跃非线性系统,研究了异步有限时间滤波问题;Yan 等[15]研究了具有半Markov 随机系统的有限时间稳定性和镇定问题;苏磊等[16]综述了半Markov 跳跃系统的稳定性与控制器与滤波器的设计;Ren 等[17]研究不确定正Markov 跳跃神经网络的有限时间有界性和镇定问题。然而,上述研究成果中没有考虑脉冲对系统有限时间稳定性的影响。鉴于此,针对一类具有Markov 切换的脉冲随机时滞系统,通过选取模态相关的泛函和利用平均脉冲区间条件来降低判据的保守性,建立系统的有限时间稳定准则,以期实现脉冲随机时滞系统的有限时间稳定。
1 预备知识及定义

2 主要结果

因此系统(2)是关于 (c1,c2,T)的均方有限时间稳定。证明完毕。
注1 通过定理1 中 αi>0 , µi≥1以及式(20)可看出Lyapunov 函数是呈指数发散的,所以系统(2)并不是Lyapunov 意义下的稳定,由此可看出一个系统有限时间稳定并不一定代表其是Lyapunov 意义下的稳定。
注2 由于考虑了具有Markov 切换时滞系统,当模态数目增加时,需求解的LMI 的维度变大,且矩阵中的元素数也会增多,使计算量增加,LMI 的求解复杂度上升。为解决这个问题,在定理1 中采用分块矩阵技术将大的矩阵分解成小块,以降低计算的复杂度。若系统(2)为不考虑脉冲影响的随机Markov 系统:

3 反馈镇定
根据定理1,设计反馈控制器使系统(2)满足有限时间镇定,考虑如下形式的状态反馈控制器

则式(35)等价于式(29)。同理,对式(6)左右同时乘以Xi,即可得到
则式(36)等价于式(30),由定理2 可得系统(2)在式(26)作用下是关于 (c1,c2,T)的均方有限时间稳定。
4 实例仿真

其中Q3的最大特征值 λ5=0.977 6,其余矩阵对应的特征值如表1。

表1 对应矩阵的特征值Tab.1 Eigenvalues of corresponding matrices
考虑N0=2 , τ*=0.15 , ε=0.1,则系统的脉冲序列如图1。设系 统(2)的 初值ξ(ϑ)=[-0.4,0.3]T,ϑ ∈[-0.2,0] , 则c1=0.25 。 若考虑系统t∈[0,1.5],将上述求解的特征值与假设值代入式(23),得出系统(2)是关于(0.25,9.75,1.50)的均方有限时间稳定。作500 次样本轨道,并取期望值,得到系统的均方状态轨迹,如图2。
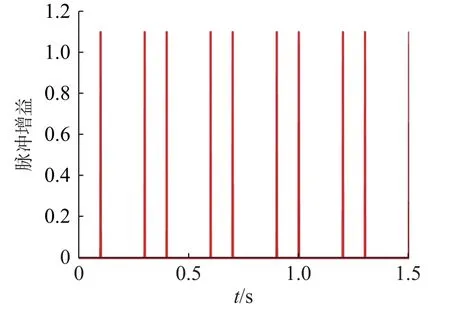
图1 脉冲序列Fig.1 Impulsive sequence
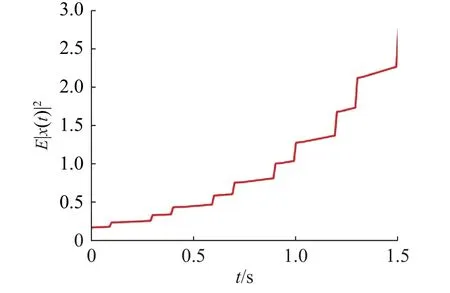
图2 系统的状态轨迹Fig.2 State trajectory of the system
验证定理2 中反馈控制器的有效性,根据上面求出的矩阵易得

图3 为加入反馈控制器后的均方轨迹状态。从图3 可看出:系统(2)在式(26)作用下同样是关于(0.25,4.64,1.50)的均方有限时间稳定。
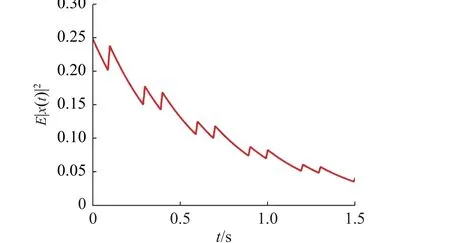
图3 反馈控制下系统的状态轨迹Fig.3 State trajectory of the system under feedback control
注4 通过MATLAB 中LMI 工具箱,式(4)和式(5)在不同模态下的可行性解被求解出来,验证了判据的正确性。由于选取的泛函考虑不同模态及判据中包含时滞信息,降低了判据的保守性;同时利用平均脉冲区间条件,仅对平均脉冲区间 τ*施加限制,进一步降低了判据的保守性。
5 结论
针对一类具有Markov 切换的脉冲随机时滞系统的均方有限时间稳定性问题,通过利用L-K 泛函法以及随机分析技巧,建立系统有限时间均方稳定的充分条件。基于所得的充分条件,设计使系统满足有限时间稳定的状态反馈控制器,并给出实例进行验证。通过选取模态相关的泛函且利用平均脉冲区间条件对脉冲区间的上界或下界没有限制,而且仅对平均脉冲间隔提出要求,降低了保守性。带时滞脉冲和Markov 切换的随机系统的有限时间问题有待进一步研究。

