基于改进蚁群算法的光纤光缆铺设路径规划∗
王 帅 孙晓伟 刘家旭 刘 洋
(1.青岛科技大学信息科学技术学院 青岛 266061)
(2.中国矿业大学煤炭资源与安全开采国家重点实验室 徐州 221116)
1 引言
近些年来,由于科技进步,电力通讯行业发展迅速,当今社会对电力通信的需求也越日益增加,光纤光缆[1]成为了电力通信的主要部分,所以对光纤光缆的路径规划问题是最先需要解决的,要合理地规划路径,使前期便于光纤光缆布设后期维护方便,同时还要兼顾其成本。光纤光缆铺设有架空和地线传输等几种铺设方式,根据不同地形合理布设不同类型的光纤光缆,蚁群算法[2]是一种启发式的仿生优化算法,由Dorigo 等提出[3],主要为了搜寻蚂蚁窝和食物之间的距离最小的路径[4]。因此我们能够将蚁群算法应用于光纤光缆的铺设路径当中。蚁群算法不但与别的算法更好搭配[5],也有精确度高、运行速度快[6]等优点,但同时也存在迭代时间长次数多,随机性高,死锁概率高等弊端,使其在寻优过程中还有进步的空间。所以应该改良基础蚁群算法来改善上述问题。
对路径规划问题,相关研究人员做了很多工作,获得了优异的成绩。陈鑫等[7]为了增强无人机的安全飞行性能,首先,提取地形地貌特征点作为无人机飞行航迹点,将航迹规划问题转化为旅行商问题。其次,提出了一种自适应信息素更新方法和局部信息素的改进蚁群算法,实验显示改进后的蚁群算法具有实用性和优越性,有效地解决无人机路线规划的问题。但是,优化过程中仍有收敛时间过久的问题。刘学芳[8]通过建立信息素矩阵,分别加入激励函数,改进信息素更新方式,用不同的刺激情况分析信息素和挥发系数对算法的影响,最后提出全局性人工势场算法。但是该算法对复杂环境的适应性仍需提高。贝前程等[9]提出了自适应度函数,在不改变蚁群初始参数的条件下,通过改进蚁群启发函数改进蚁群算法,改良后的蚁群算法收敛速度较快,路径距离较小,但是最终的仿真结果仍然存在迭代次数过多的问题,并且该实验仅在一种环境下进行,缺少对比试验。
结合以上算法的结果分析,对蚁群算法改进以下方面。首先运用栅格法构建光纤光缆铺设图,找出当前点与终点的连线h1跟当前点与下个节点的连线h2的角度差ϕ,根据角度差ϕ的大小,引入环境因子A 来调整启发函数,提高了蚂蚁搜索的目的性,解决了随机性强的弊端。其次通过改进挥发系数的挥发机制,使刚开始挥发系数较大,增加初始阶段蚂蚁搜索全局性[10],到收敛后期,伴随迭代次数的增多,挥发系数慢慢减小,不仅避免了算法的停滞,而且使算法的迭代速度增加,从而得到最优解。
2 问题描述及环境建模
2.1 问题描述
本文光纤光缆的铺设路径规划问题可以描述为从起始点开始通过地下或架空的方式向目标点布设光纤光缆,该路径要避免与地上和地下建筑物冲突,同时要兼顾工程成本和完成质量,则必须合理地规划光纤光缆布设路线。
2.2 模型构建
光纤光缆铺设路径规划系统对于大型建筑物以及周围植被山川河流是已知的,这时可以把建筑物、植被、河流、山川统一视作光纤光缆铺设地图的障碍物,光纤光缆到障碍物的不同距离对动态光纤光缆铺设路径规划系统的影响不同,光纤光缆到障碍物的距离见表1。


表1 光纤光缆到障碍物距离对铺设的影响
2)光纤光缆到各障碍物距离可行参数不能超过1且之和不能超过4。
3)所有基站都必须连接完毕。
因此,本文光纤光缆铺设最优路径目标值为
运用栅格法构建光纤光缆铺设的地图,如图1所示,浅色栅格意为该栅格可铺设,深色栅格意为该栅格不可铺设。

图1 障碍物栅格图
3 蚁群算法原理

α是该算法的信息素因子[13],代表着(i,j)这条路径上信息素的重要程度。β是该算法的期望启发函数因子[14],dk为蚂蚁k 未访问的节点集合,τij、τis分别为路径(i,j)、(i,s)上的信息素浓度,ηij、ηis分别为从i 点到j 点和s 点的启发式因子[15],公式为
其中dij、dis是i点到j和s点的最短直线距离,其公式为

Q 是信息素增强系数[21],是常数,该系数能左右算法的收敛速度。Lk是蚂蚁k 经过每一个节点所走的路线长度。
在未访问之前,节点间的初始信息素相等,在蚂蚁走完每个节点之后,会重新更新该路线上的信息素,根据蚁周模型运算每个蚂蚁发出的信息素,算出增加的信息素大小。与此同时也要考虑挥发的信息素大小,通过运算得到最终的信息素量。由于蚂蚁对下一节点的转移概率受启发式因子和更新信息素共同影响,因此也要考虑启发式因子对转移概率的影响,两者共同作用指导蚂蚁到达目标点。然后进行数次循环,得到最优解。
4 改进蚁群算法
4.1 改进启发函数
路径规划初始阶段,蚂蚁会通过轮盘赌的形式选取下一节点,由于蚂蚁不清楚目标点的具体位置,这会造成蚂蚁在找寻路径时,表现得不知所措,随机性比较强,增加了收敛时间,针对这个问题我们对启发函数进行调整,引入环境因子A,使得目标点对蚂蚁有一个向导作用,具体方法如下:
假设蚂蚁在i 点,下一个要到的节点为j,目标点为e。i点与下一个要访问的节点j之间的角度为θij,θij的取值范围为{0,45,90,135,180,-135,-90,-45},i点与目标点e的夹角为γie:
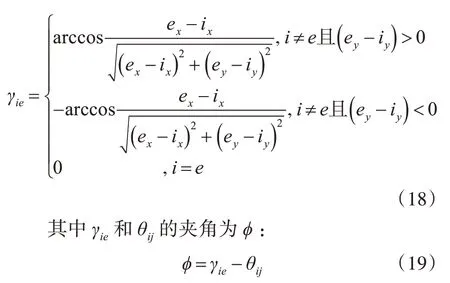
此时引入环境因子A,对启发函数按下式进行调整。当ϕ在区间(-45,45)时,则A≤1。当ϕ在区间(-45,45)以外时,A >1。更有利于算法的调整,如下式:
当角度ϕ在设置的范围区间(-45,45)时,说明蚂蚁k 在朝着目标点的方向前进,此时环境因子A≤1,蚂蚁在访问下一节点时朝该方向前进的几率会越来越高,反之亦然。
此时状态转移函数为
4.2 改进信息素挥发系数
随算法循环次数增加,路线上的信息素会挥发减小,用ρ来表示,挥发系数ρ的高低会左右搜索能力和运行时间。假如ρ太小,说明挥发速度很慢,导致蚂蚁重复选择已经访问的路线,改变全局搜索能力。反之ρ太大,导致收敛时间过长。所以本文找到随迭代次数大小进行调整的信息素挥发系数关系式,如下式:
K 为蚂蚁迭代次数,B 为一个常数。在算法初级阶段为了快速得到最优解,提高蚁群的搜寻能力,ρ的取值应该比较大;到了后期,随着迭代次数越来越大,挥发系数ρ的取值慢慢变小,减小了信息素对蚁群的影响,防止了算法停滞不前,减少了收敛时间,从而取得更优的解。
5 仿真实验与分析
本实验在Matlab R2018a 平台下,构建简单环境和复杂环境两种实验环境,文中设置两个路径规划环境分别为20×20 个栅格的简单环境,障碍物比较少;30×30个栅格的复杂环境,障碍物比较多。
实验一建立一个20×20 的随机栅格地图环境,图2 所示。该蚁群算法的参数设置:蚂蚁的个数m为50,迭代次数100 代,初始信息素挥发系数ρ为0.4,α为1,β为5,Q为1,A取0.9或1.1,B为0.4。

图2 简单环境下两种蚁群算法路径轨迹对比
两种算法在简单环境下进行50 次实验,并分别记录路线长度与迭代数目,算出平均路径长度,从图3 可以看出,迭代数目明显减少,且收敛速度更快,由表2 得到平均路径长度减少1.5297m,迭代次数减少24 次,收敛时间减小了16.78s,路径长度得到减小,迭代次数相比于未改进的也减少了很多。
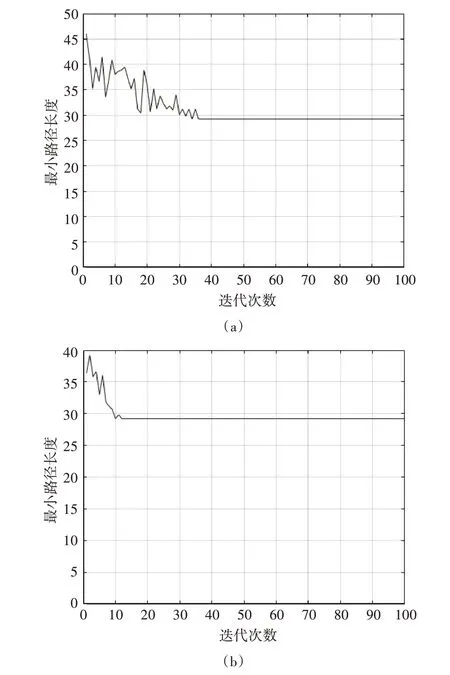
图3 简单环境下两种蚁群算法收敛曲线对比

表2 简单环境下两种蚁群算法对比
实验二,现实光纤布设情况比较复杂,简单环境下光纤铺设轨迹路径并不能反映改进蚁群算法的适应性,因此构造一个30×30 复杂环境的随机栅格地图,如图4 所示,该蚁群算法参数设置:蚂蚁的个数m 为50,迭代次数100 代,初始信息素挥发系数ρ为0.4,α为1.4,β为5,Q为1,A取0.9或1.1,B为0.4。

图4 复杂环境下两种蚁群算法路径轨迹对比
两种算法在该复杂环境下进行50 次实验,并分别记录路线长度和迭代数目,算出平均路径长度。从图5 可以看出,迭代数目明显减少,且收敛速度更快,由表3 可以得到,复杂环境下,平均路径长度减少了3.936m左右,迭代次数减少了69次,收敛时间减少了3.44s左右,路径长度得到减小,迭代次数相比于未改进的也减少了很多,并且能很好地适应复杂环境。
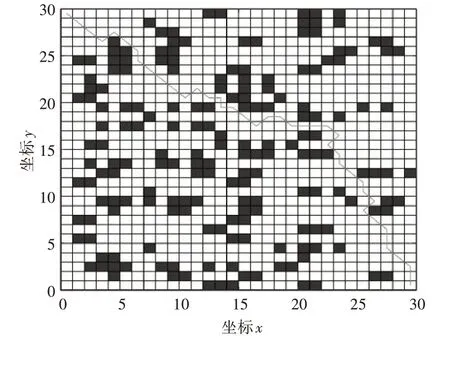

图5 复杂环境下两种蚁群算法收敛曲线对比

表3 复杂环境下两种蚁群算法对比
6 结语
本文从光纤光缆铺设路径优化问题出发,结合改进蚁群算法,来求得铺设过程中最优路径问题,文中引入环境因子来调整启发函数,降低了蚂蚁搜寻的盲目性,解决了随机性强的弊端。通过改变信息素挥发系数,增加初始阶段蚂蚁搜索的全局性,使收敛次数明显减少。最后仿真结果显示,改进后的蚁群算法,收敛速度明显增加,具有较强的路径搜索能力和适应能力,使光纤光缆的铺设成本大大降低。

