一种改进的视图几何基本矩阵估计法∗
夏子山 王韦刚 吴 豪
(南京邮电大学电子与光学工程学院柔性电子(未来技术)学院 南京 210023)
1 引言
近年来,多视图几何成为计算机视觉领域的研究热点,它关系到计算机视觉领域的许多研究,如视觉SLAM[1]、摄像机标定[2]、立体匹配[3]、目标识别与跟踪[4]等。基本矩阵包含了两视图的几何信息,准确求解基本矩阵对于视图几何十分重要。基本矩阵的求解通常需要利用特征提取算法得到两视图上的对应点,常用SIFT、SURF、FLANN等算法[5~7]。通过对应点估计基本矩阵的方法可以分为线性估计法、迭代估计法和鲁棒估计法。线性估计法有线性最小二乘的八点法[8]等。文献[9]根据基本矩阵的七个自由度,提出七点法来估计基本矩阵。若两幅图像之间是平移运动,文献[10]提出用五个点估计基本矩阵。这些线性估计法是快速的,但是使用的点对较少,算法对噪声更敏感。非线性最小二乘法[11]是经典的迭代法,但是它抵抗错误匹配的性能差,因为在同一场景中摄像机通过平移和旋转变换视角拍摄照片时,会遇到遮挡或光线的变化。这会产生错误匹配点,导致基本矩阵估计的不准确。对此,一些研究者提出了各种抗干扰的鲁棒性算法,如最大似然估计法(Maximum-likelihood Estimator,M-Estimator)和最小中值二乘法(The Least Median of Squares estimator,LmedSe)[12]和随机抽样一致性算法(Random Sample Consensus,RANSAC)[13]。随机抽样最大似然算法(Maximum Likelihood Estimation by Sample and Consensus,MLESAC)[14]是 在RANSAC 的基础上结合了先验条件,能有效提高检验准确率。这些鲁棒性算法的核心思想是基于假设检验策略独立地去除异常点。因为需要多次随机抽样测试,每个测试过程都涉及到所有数据集来区分内部值和异常值,所以它们的计算成本较高,处理速度较慢[15]。文献[16]提出了一种快速迭代的方法,能快速剔除集合中的离群元素。文献[17]受此启发提出了一种通过对极约束快速迭代剔除错误匹配点的基本矩阵估计法,但仅仅依靠对极约束仍会保留少量非对应点。
基于上述背景,我们提出了基于梯度的离群点剔除约束算法(Outlier Screening by Gradient and Constraints,OSBGAC)估计基本矩阵,该算法首先针对含有非对应点的情况,通过基于对极约束梯度迭代来快速剔除部分非对应点。然后施加对应点相关性的约束,剔除梯度迭代无法识别的非对应点,得到最佳对应点集合去估计基本矩阵。实验结果表明,相比于其他算法,本算法估计基本矩阵准确度有所提升。
2 对极几何与基本矩阵的线性解
两视图几何的场景如图1 所示,点P 是三维空间中的一点,平面π′是平面π在空间中作旋转平移变换后的另一平面。点P 在平面π和π′上的投影 点 分 别 是mi和m′i,li和li′是 对 应 点 的 极 线。对极几何描述的是两幅图像之间点与线之间的关系,可以用基本矩阵来描述。对极几何仅由摄像机和它们的相对位置、内部参数决定,而非场景结构。对应点的齐次坐标可表示为mi=(ui,vi,1)T和。则有对极约束如式(1)所示:
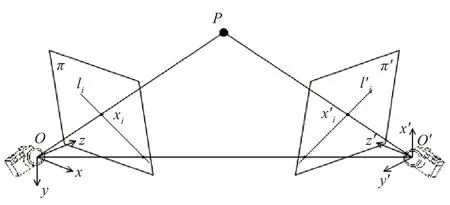
图1 两视图几何

式(1)也可以写成式(2)的形式:
式中Ai是1×9 的向量,可由像素点齐次坐标的克罗 内 克 积 表 示 为Ai=(u′i,v′
i,1)⊗(ui,vi,1)=(uiu′i,uiv′
i,ui,viu′
i,viv′
i,vi,u′
i,v′
i,1)。f由基本矩阵F的元素构成,f=(F11,F12,F13,F21,F22,F23,F31,F32,F33)T,Fij是基本矩阵F第i行j列的元素。根据八点法可知,已知八对匹配点的情况下可以求解向量f,进而计算出基本矩阵,但图像易受噪声干扰使得点对存在偏差。针对这一情况,通过从多组点对估计出基本矩阵,能有效地减少误差[18]。将一对点拓展到n对点可得到下式:
式中A=[A1;A2;…;An]。计算AT A的最小特征值所对应的特征向量即可得到向量f。
3 算法原理
3.1 基于梯度的基本矩阵估计
一般情况下最小化对极约束得到基本矩阵解的误差很大,只有在每对点的对极约束方差相同时才能得到准确的解。为避免这种情况,可通过式(4)最小化对极约束的加权平方和去求解基本矩阵:
其中σi是每对点对极约束的方差。因为图像上的点是由同一算法提取,每个点可以看作受到的噪声都服从独立的高斯分布,可由式(5)表示噪声的协方差矩阵:
噪声通常是未知的,可以通过一阶近似得到方差的表达式:
每一项同乘常数不影响优化问题的求解,式(4)问题则可以写成式(7):
3.2 OSBGAC基本矩阵估计法
在理想状态下,矩阵A对应的秩是1。在两幅不同图像上的对应点通常用匹配算法得出,但实际中总含有错误匹配的点对。错误的匹配点使得矩阵A的特征值均不为零,而影响求解基本矩阵的准确程度[19]。为去除不匹配点,提高基本矩阵F的求解准确度,我们提出OSBGAC算法。首先将求解F矩阵转换为式(8)最优化问题的表达式:
式中W=diag(w1,w2,…,wn)权重矩阵用于选择剔除异常的对应点。通过迭代求解最优矩阵W和向量f。算法初始时将全部对应点带入计算,并将矩阵W初始值设置为单位矩阵In×n。通过计算每一对匹配点的迭代误差εi去更新权重矩阵W。εmax是从上一轮迭代的误差值排序后选取下五分位Q20%(εi),δ为经验值,则有:
由上节可知,迭代误差εi仅依靠最小化对极约束不足以得到最优解,第i对匹配点的第n次迭代误差表示为式(10),用来计算权重矩阵。
经上述迭代筛选匹配点后,仍存在少量符合对极约束的但并非匹配的点对。误差通常是由图像中的噪声引起,导致匹配算法不稳定。一般情况下,匹配点对的误差可分为定位误差和离群误差。定位误差是指配点有少量的偏移,通常在几个像素内。离群误差是指特征点的错误匹配,点对不能成为对应点。离群点通常会带来很大的误差,即使只有少数点对也会严重降低图像几何估计的精度。
为尽可能地剔除离群点,提高基本矩阵估计精度,所以需要再寻找新的约束[20]。由于同一空间下的两幅图像之间存在旋转平移关系,正确匹配点对的位置关系也存在一定的相关性。根据对应点的这一特征,设计筛选算法用于剔除剩余非对应点。已知点对和mi的m′齐次坐标,计算点对之间的欧式距离di:
其中点对之间连线与水平方向的夹角为
我们提出用向量ci来描述点对的关系特征。
其中n对点的关系特征矩阵可以表示为C=[c1,c2,…,cn],进而可以由下式计算每对点特征之间的皮尔森相关系数rj,k。
式中cj,i是矩阵C中第j行i列的元素,cˉj是矩阵C第j行元素的均值。通过计算可得到的相关系数,再剔除相关性较小的点对,而保留相互相关性强的点对再次更新权重矩阵W。计算ATWA的最小特征值所对应的特征向量即可得到向量f。OSBGAC基本矩阵估计算法流程如下:

计算最后用来估计基本矩阵的匹配点的误差,然后通过均值衡量算法的准确度。
4 实验评估
为了验证算法求解基本矩阵的精度,本文在四个场景下各选取两幅图像进行实验。通过SURF算法取多维特征,使用K值近邻算法匹配特征最相近的点作为对应点去估计基本矩阵。实验硬件环境:AMD Ryzen 5 3500U,主频2.1GHz,内存16GB。实验软件环境为Matlab R2018a。
图2 中4 个子图是室内环境下,不同视角的两张图片在算法各个阶段筛选匹配点的过程。图2(a)是由SURF算法初始得到的匹配点对,并圈出将其用连线连接。可以看到初始匹配点中含有大量的错误匹配,因为图像不可避免受到光线变化和噪声等影响,使匹配算法产生错误匹配。错误匹配点会严重影响基本矩阵计算的准确程度,需进一步处理以剔除错误匹配点。


图2 场景下算法各个阶段筛选匹配点
图2(b)是经过迭代剔除误差较大匹配点对迭代后的情况,可以看出图2(a)中杂乱的错误匹配大部分被剔除,匹配点间的连线也都呈现同一方向。但仍有少部分的错误和与其它连线交叉的匹配点对,如书籍与电脑屏幕和水杯上下不同位置的错误匹配。图2(c)是在前两个过程剩余点对上施加点对特征的约束后得到的,可以看出错误的匹配点基本消除,图片只存在少量键盘位置的错误匹配点对。再经过一次迭代筛选,图2(d)获取了最佳匹配点对集。
为了测试不同算法在四个场景下的性能,我们列出表1 估计基本矩阵的误差均值和方差,同一场景中表现最好的数据已用粗体标出。所对比的算法有:本文算法OSBGAC、M-Estimator、LmedSe、RANSAC、MLESAC 和 本 文 未 加 约 束 的OSBG 算法。从表中数据可以得出,本文的迭代估计在加上匹配点约束后在每一个场景下误差都得到了减小。场景一中本文算法性能最好,其次是LMedSe和RANSAC 算法。因为场景错误匹配点较多,M-Estimator 和MLESAC 算法表现并不理想。图3场景的特征明显,初始匹配准确度高,各算法表现都不错,其中本文算法误差最小。图4 场景在光照差异影响下个算法误差整体相比场景一和二都有增加。本文算法相比其他算法误差最小,效果最好。MLESAC 算法与本文算法性能接近。其余算法受影响较大表现不稳定,误差较大。图5 场景处于强曝光环境,本文算法在此场景中性能最佳,较其他算法误差均值至少降低20%。其次是LMedSe和MLESAC算法。

表1 四个场景下各算法表现

图3 图画高相似场景

图4 建筑昼夜场景

图5 雕塑强曝光场景
从以上实验结果看,M-Estimator 和RANSAC算法在有干扰的情况下表现不佳,LMedSe 和MLESAC算法表现较好,本文算法在上述四个场景中估计基本矩阵最佳。
当在场景一的图像上分别增多添了30%、50%和70%比例的异常点时,测试各算法的鲁棒性如表2 所示。异常像素点是在原有的像素上添加均值为0,方差为0.1 的高斯噪声。从表2 中可以看出,不同情况下的同一算法性能浮动很大。这是因为噪声严重影响匹配过程,错误匹配点会导致基本矩阵估计的误差增大。当异常点高于50%时,M-Estimator和RANSAC算法以超过其处理能力的边界,误差过大。LmedSe 和MLESAC 算法在不同情况下的误差浮动很大。本文算法表现较好,鲁棒性能力最佳。

表2 异常点比例不同情况下的各算法表现
表3 是各算法在四个场景下的平均运算时间和算法复杂度。传统算法中MLESAC 的样本抽样次数最多,运行时间最长,但其估计基本矩阵误差小。其他传统算法抽样次数少,运行时间短,但准确度低。本文算法迭代次数少,在保证准确度的情况下运行时间较MLESAC算法下降了64.4%。

表3 算法复杂度和平均运算时间
5 结语
针对错误匹配点影响基本矩阵估计这一问题,本文改进了基本矩阵估计算法,并在迭代的过程中给匹配点添加新的特征约束,能有效剔除残留错误匹配点。本文算法处理不同场景下的图像与其他算法估计基本矩阵相比,有更高的准确度。对于处理带有噪声异常点的图像,本文算法也具有更好的鲁棒性。然而,在筛选错误匹配点的过程中有很多正确匹配点被剔除,使得剩余对应点都较为集中。对此,也为今后研究如何尽可能利用图像的全局信息估计基本矩阵奠定了基础。

