借助几何画板 渗透模型意识

孟繁晶 徐泽能

《义务教育数学课程标准（2022年版）》指出：数学模型意识是小学数学核心素养的主要内容之一，模型意识主要是指“对数学模型普适性的初步感悟”，模型意识的主要表现是“知道数学模型可以用来解决一类问题，是数学运用的基本途径；能够认识到现实生活中大量的问题都与数学有关”。

“几何画板”是一套用于数学教学的软件，是数学教师用于数学教学的“利器”。随着“双减”政策的进一步落实，减负提质工作更是重中之重。“几何画板”可视化教学的实践与研究，化繁为简，化抽象为生动，以生动的案例激发了学生对几何的学习兴趣，发展图形与几何问题解决的模型意识，极大地提高了课堂学习效率。在教学图形与几何内容时，部分学生仍然感觉到学习几何非常困难，教学实践表明学生所缺乏的正是实际生活经验，动手能力偏弱，观察能力不强，“几何画板”可视化教学正是可以让学生参与其中，还原体验。

一、借助操作活动，展现知识发生过程，初识等长变形模型

“几何画板”作图原理就是大家十分熟悉的“尺规作图”，经它绘制出的几何图形，即使图形的位置和形状发生了变化，但图形原有的几何性质不会发生改变，这或许是它又被誉为“动态几何”的真正缘故。“几何画板”函数图象（两个变量）的绘制和测量功能，能直观地展现数形结合的思想，将运动中的图形的性质和数量关系展现得淋漓尽致。通过对动态图形测量数据的分析和研究，有利于发现图形的性质和规律。而对动态图形的测量又能对已有的猜想和结论加以验证，较好地展现了知识的发生过程，为师生创设了一个具有探究功能的实验环境。

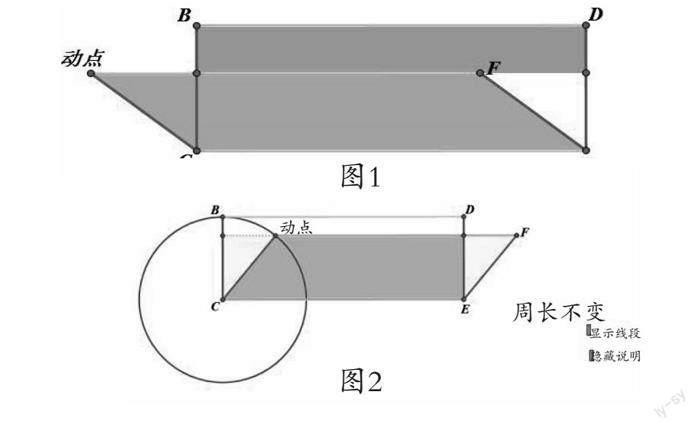
案例1：把一个长方形拉成一个平行四边形，它的周长和面积会发生变化吗？

师：在拉的过程中，到底有哪些量在发生变化呢？

生1：长还是宽呢？

生2：借助学具拉动，发现周长并没有发生变化。

生3：虽然有拉动，但是面积大小变化不太明白。

师：拖动图1的几何画板。

生：长没有发生变化，宽看不出来是否变化。

师：显示以C为圆心，宽为半径的圆，如图2。

生：圆的半径不变，长和宽都没发生变化，所以周长不变。

师追问：面积有变化吗？说说你的想法？

生1：面积变小了，因为底是长方形的长，高变小了。

生2：变成平行四边形之后，可以把平行四边形通过割补，转化为直角梯形和直角三角形的和，得到一个新的长方形，比原长方形少出上方空白处长方形的面积。

评析：等长变形，长方形拉成平行四边形周长和面积的变化是一个教学难点，让学生先经历猜想、操作，再运用几何画板验证，直观地解释为什么长方形拉成平行四边形，周长是没有发生变化，而面积的变化通过割补的方式可以看出是变小的，图2利用圆的半径来解释长、宽，学生在这个阶段还没有学过圆的半径等内容，可作为拓展内容让学生了解。利用几何画板还原体验，让学生在直观中建立模型意识，化静为动，动中取静，将数学问题趣味化、多元化。

二、借助猜想验证，把握变与不变，渗透等积变形模型

等积变形是指在图形或者是形状发生改变的时候，这个变形过程中的面积不发生变化。在教学过程中，借助猜想验證，能让学生在变与不变的全面把握中渗透等积变形模型。

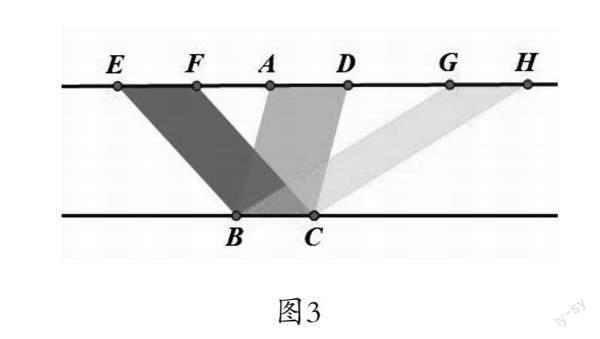
案例2：图3中两条平行线之间平行四边形的关系？

师：从图中你能了解哪些数学信息？

生1：三个平行四边形的面积相等，但是周长不同。

生2：因为平行四边形的面积与底和高有关，这三个平行四边形的底是相等的，又因为是在平行线之间，所以单个平行四边形的高是相等的，所以这三个平行四边形的面积相等。

生3：为什么周长不同？

生4：因为他们虽然其中一组边长度相等，但是另一组边的长度是不断变化的，所以周长不同！

生5：老师，如果有具体的数据我们可以算一下？

师：表扬同学们善于利用所学的知识解决问题。（给出相关的数据）

生1：经过计算这三个平行四边形的面积确实相等，并且周长不同，如有平行线之间还有其他的平行四边形，那它们的关系又是什么呢？

生2：面积还是相等的，但是周长不同，因为只要是平行线之间的平行四边形高都相同，只要它们的底相等，那么它们的面积就相等，其实就是等底等高的平行四边形，面积相等！

师：让我们一起来验证一下同学们的猜想。（拉动其中一个平行四边形，几何画板会显示面积和周长的数据，从而验证同学们的猜想）

生：面积相等，形状不同。

师：这在我们数学中叫做“等积变形”。请同学们还有什么问题？

生：那两条平行线之间的三角形，它们的关系又是什么？（生画图）

师：在几何画板上进行，如图4。

生：因为三角形面积是底乘高，这三个三角形的底相等，因为在两条平行线之间，所以相等的底对应的高也是相等的，等底等高，所以这三个三角形的面积相等，但是周长不相等。

师：同学们能从平行四边形联想到三角形，从一个问题联系到一类问题。

学生进一步根据数据验证猜想，教师用几何画板进行展示验证学生猜想。

评析：学生经历数学建模后，教师应引导学生进入更深层次的迁移类推，等底等高的平行四边形面积相等，这个模型同样适用于三角形等图形中，让知识、方法和思维结构化、可视化，不断深化对相关模型的渗透。

三、借助化繁为简，放手自主探究，拓展等积变形模型

弗兰登塔尔曾说过：数学教学应教给学生充满着联系的数学，只有进行链接和沟通，才能把握数学的本质。也有的学者指出，化繁为简，是学习数学最有效的策略。教学中要借助化繁为简，给予学生自主探究的时间和空间，从中拓展等积变形模型。

案例3：大正方形的边长是3厘米，小正方形的边长是2厘米。怎么求出图6中阴影部分的面积？

生：老师，这个题目是不是缺少条件呢？阴影部分是三角形，需要知道底和高。

师：想一想可以运用我们之前学习的哪些模型解决这个问题呢？

生1：我们可以利用割补法，然后平移。

生2：我们还可以利用之前讲过的平行线之间的距离都是相等的，然后对三角形进行变形。首先利用正方形的对角线画出平行线IK∥GE，拖動三角形在平行线上的点，变形为图7（1），其实就是大正方形面积的一半。

生：那无论在平行线上的点怎么移动，图7（1）、图7（2）和图7（3）的面积都是相等的。

师：像这样的题目生活中还有很多，我们要善于去观察，寻找共同点。在原来的基础进行拓展。

评析：等积变形比较适合计算一些较复杂的、较难的平面图形的面积，有时计算阴影部分面积会缺乏一些信息和条件，但能在图中找到和它等积的图形，若能算出与它等积的图形面积，即可求出阴影部分的面积。化繁为简，学生在自主探究中建构数学模型，沟通一个问题和一类问题的联系，积累数学活动经验，这是模型意识不断发展的过程。

四、借助作业设计，探究知识本质，运用等积变形模型

为了让学生进一步体会等积变形在生活中的运用和在数学中的价值设计如下的作业设计。

案例4：研究长方形面积的，设计图案是阴影部分的面积是长方形面积的。（1）尽量多设计几种不同的方案。（2）看谁设计的独特、新颖。

学生在学习单上进行设计，教师可利用几何画板进行操作验证。重点引导学生观察以下几幅图的设计。

师：同学们，这位同学画（如图8）的阴影部分面积是长方形面积的吗？

生1：看不懂。

生2：在图中画一条线，同学们就看明白了。（如图9）

生3：利用之前所学的平行线中的等积变形，同样可以解决这一类问题。

师：同学们能多维反思，内化并完善所学知识，希望能把所学运用到我们生活中的每一个角落。

评析：数学模型的建构和完善不仅是在课堂教学中，还应该存在于我们开放性的作业中，借助数学推理探究知识本质，逐步形成运用模型进行思维的习惯，在自主探索中不断丰富模型的内涵和外延。

总之，发展学生的模型意识需要一个长期的过程，教师要有意识地将模型思想渗透到日常教学中，使学生在知识形成和运用的过程中逐步形成和发展模型意识。借助几何画板渗透模型意识，不仅加深学生对数学模型的理解，同时促进学生内化和丰富数学模型，使学生形成良好的思维习惯和数学素养。