递推:贯穿数列教学的始终

江苏省溧阳中学 (213300) 徐 兰 黄俊赟

递推是数列的灵魂,是序列计算的一种常用算法,是按照一定的规律来计算序列中的每一项.其思想是把一个复杂的庞大的运算过程转化为简单过程的多次重复.已知一个数列{an}第1项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系用一个公式来表示就是这个数列的递推公式.这是数列的一种表示方法.递推是数列的本质属性,也是它与其他函数的最大区别,本文从递推的视角来纵观数列全章.

1.递推的初步理解——等差、等比数列的通项、求和公式推导

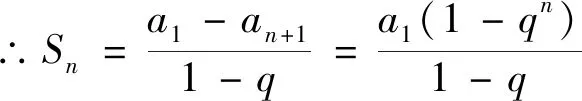
2.递推的深度应用——累加法、累乘法的另辟蹊径

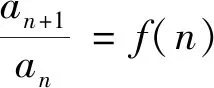
3.递推的深刻理解——一般数列求和方法的豁然

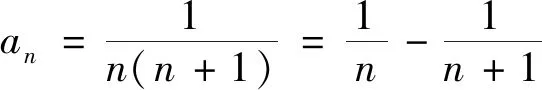
4.递推的综合应用——高考命题的热点

建立数列的递推关系是数列的应用和其他数学知识结合的重要方法,也成为数列试题重要的命题方向.2023年全国新高考Ⅰ卷第21题,通过全概率公式构建了数列的递推关系,是数列与概率的综合.23年的上海数学高考题考察了数列与函数的综合,也是运用迭代思想解决问题.

题目:甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.

(1)求第2次投篮的人是乙的概率;

(2)求第i次投篮的人是甲的概率;

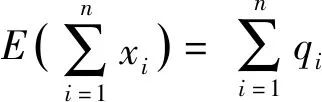
解:(1)设“第i次投篮的人是甲”为事件Ai,“第i次投篮的人是乙”为事件Bi,则P(B2)=P(A1·B2)+P(B1·B2)=P(A1)·P(B2|A1)+P(B1)·P(B2)|B1)=0.5·0.4+0.5·0.8=0.6.

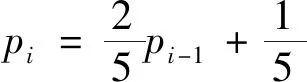
数列的综合应用问题中,搞清事物发展的前因后果及其相互联系,搞清事物的形成过程和形成方法,是寻找解题思路,突破难点的必经之路,用递推的方法来表达事物间的联系能够让我们对所解决的问题以数学的方式呈现出来,其实就是建立数学模型的过程。建立递推关系,是解决这类综合问题的核心环节.只有真正理解递推,才有能力在实际情境中用数学的眼光来观察问题,用数学的知识来表达问题.

递推蕴含着转化、迭代、程序化与机械化等思想.在数列的教学过程中,教师要抓本质,重点体现“逻辑思维能力”,渗透思想方法,在关键处多着力,靶向新高考的热门题型与教学中的难点问题,提升学生的关键能力.