优化数学认知结构 提升一轮复习效率——以“函数零点”复习课为例

福建省浦城县第二中学 (353400) 黄慧美

一轮复习是高考复习教学的关键一环.在此阶段,学生依然是课堂的主体,然大多复习课堂却以教师为主导,延续着“师讲生听”的教学模式,课堂容量大、频率快,容易出现学生“懂而不会”的尴尬局面.实际上,一轮复习要重视通性通法的提炼,让解题方法和解题策略更具系统性和方向性,使复习更高效,解题更流畅.本文笔者以“函数零点”复习为例,以典型问题为切入点,引导学生在巩固基础知识的同时,掌握解题通法,构建数学思想方法体系,进而优化认知结构,提升复习效率.

一、教学实录

1.明确方向,激发欲望

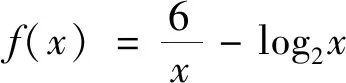
A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)

在复习阶段,不能将目光定位在解题上,而是要透过题目了解考试动向,分析核心考点,进而进一步巩固“双基”,扫清解题障碍.

师:题中涉及到什么概念?

生齐声答:函数的零点.

师:函数零点的概念大家还记得吗?

生1:使函数f(x)=0成立的实数x叫函数y=f(x)的零点.

师:很好,那么想一想例1该如何求解呢?

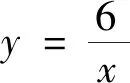
生3:生2的解法没有问题,解题时既要画图又要代值,我觉得这个问题可以换个思路来解,可以考虑应用零点存在的定理来解答.

师:说说你的解题思路.

师:很好,通过代数法和几何法都顺利地得到了答案.生2是从定义的角度去考虑,首先将函数零点问题转化为方程的根,然本题方程难以直接求解,为此又继续转化,将其转化为函数的交点问题,最后利用数形结合的思路精准地求得了答案,这是解决此类问题的一个常用的方法,看来大家已经掌握了解题的精髓.生3结合题目特点,根据零点存在定理巧妙地解决了问题.

师:如果例1中需要求零点的个数,生3的方法还有效吗?

通过交流,学生运用不同的解题方案顺利地求解了问题,通过剖析发现解决此类问题可以从代数和几何两方面入手,同时体验了数形结合思想和转化思想在解题中的重要价值,为了进一步强化认识,教师又给出新问题,引导学生继续探究,不断挖掘,揭开问题的实质.

2.拓展应用,活跃思维

师:思考一下,下面问题该如何求解?

问题给出后,教师鼓励学生从不同角度思考,进而通过拓展逐渐完善认知,巩固应用.

生5:我没有画图也做出来了,通分得(1-k)x-2k=0,所以当k=1时,无实数根,当k≠1时,方程有1个根.

师:生4和生5分别从几何和代数的思路进行求解,他们的解题过程是否有问题呢?(眼尖的学生已经发现了问题)

生6:根据生5的代数式,是否要检验k一定不等于-2呢?

师:观察得非常仔细,非常好!检验会发现k一定不等于-2.其实方程简单的情况下用代数法更为方便,然在解题过程中一定要注意隐藏条件,要确保转化的等价性.如果将例2中的函数做一些改变,你认为该如何求解呢?(教师PPT给出变式)

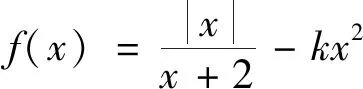
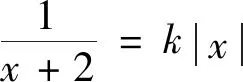
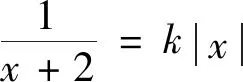
在教师的引导下,学生利用几何方法轻松地解决了问题.问题解决后,教师又鼓励学生利用代数法进行求解,然学生尝试后发现,应用代数法问题变得更加复杂了,很难求解.通过对比学生发现,处理零点问题时可以应用代数法和几何法,那么哪种方法为最优解决方案则需要根据实际问题来判断,若是简单的问题,利用代数法效率会更高,而对于较为复杂的问题,可以考虑借助图形的直观性来判断,但是应用几何法时,要使问题向容易作图的方向转化.

3.巩固强化、升华认知

师:大家看看这个题又该如何转化呢?(教师PPT展示变式2)

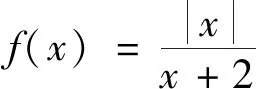
师:本题较前面问题相比,略显复杂,是关于复合函数的零点问题,这个又该如何转化呢?(教师鼓励学生进行合作探究,以此既能活跃课堂气氛,又能发挥个体优势)

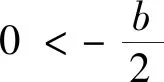
可见,通过以上的变式训练,学生已经很好地掌握了解决此类问题的方法,极大程度上提高了解题信心.虽说高考题变化莫测,然若将知识点学懂吃透,规律会自然地涌现,新题变成了旧题,复杂题变成了简单题,解题也就自然水到渠成了.

二、教学反思

在一轮复习中,以下几点应引起师生重视:

首先,在解题教学中既要掌握通性通法,又要善于结合题型和题目特点进行灵活转化.在夯实“双基”的同时,也要积累一些解题技巧,提高解题效率.

其次,教师在典型问题的处理上要遵循由浅入深,从简到繁的原则,使例子的呈现具备一定的层次性,顺应学生思维发展,提高学生解题信心.

再次,对于一些规律性的问题,需要教师的及时点拨.对关键的方法和结论进行了及时的总结和归纳,引导学生认清问题的本质,找到解题通法.

最后,教师要为学生提供巩固强化的时间和空间.教师应结合教学内容和学生认知设计变式题目,通过“变”感受通性通法的价值,体验那些不变的规律,进而深化认知,活化数学思维,锻炼学生灵活应用数学的能力.