一种应用于大尺寸测量系统的坐标系自动标定方法
张晓晖,张嘉颖,刘青,李金童,杨启航,吕佳铭,尚婷,成鹏飞
(西安理工大学 自动化与信息工程学院, 西安 710048)
0 引言
大尺寸测量技术广泛应用于航空航天设备装配、几何量精密测量、移动机器人定位与导航等工业制造领域[1-3]。随着测量对象向着复杂化,精细化,大型化,多目标方向发展,单站测量模式已经难以完成相应的测量任务。分布式测量系统相比于单站系统,具有更高的精度和更远的测量范围[4-6]。分布式测量系统通过测量单元之间组网的方式平衡了测量精度、效率和测量范围之间的矛盾,充分发挥了各个测量单元的优势。此外,分布式测量系统可以通过增减测量单元控制测量范围,并根据测量任务的需求灵活调整测量方案。
面向大尺寸测量领域的精密激光定位系统(Accurate Laser Positioning System, ALPS)是一种典型的分布式计量系统。在测量时,ALPS 的各测量单元在其独立的局部坐标系下获得测量数据。为实现多台测量单元的组网测量,需要提前标定各个测量单元的局部坐标系。测量单元的坐标系标定精度很大程度上决定了组网测量的精度[7-8]。传统的坐标系标定方法是在测量空间内部署多个已知坐标的转站控制点,各测量单元通过公共点坐标建立约束[9],从而解算出各测量单元局部坐标系之间的转换关系。一方面,公共点的布置是随机的且繁琐的。另一方面,公共点彼此之间并无关联,因此容易出现点位配对错误导致解算失败的问题。另一种常用的坐标系标定方法是基于标准器的方法[10-13]。通过将控制点集成在标准器上,利用高精度的三维坐标测量机提前标定标准器上目标点之间的距离信息或角度信息,在现场标定中作为固定参数使用。由于标准器尺寸的局限性,需要人为将标准器摆放在测量空间内多个不同位置以完成整个区域的标定。该方法相比于公共点法更为灵活,但是应用于大空间测量时的效率极为低下。另外,当测量网络中原有测量单元移站或者增加测量单元时,这些方法往往需要重新对整个区域标定。
传统的坐标系统一方法存在着精度和效率之间的矛盾,且限制了分布式测量系统增加测量单元或移站的灵活性。为了提高标定效率,吴军等提出了一种在测量单元上安装三个测量节点和一个超声波测距系统形成互扫描靶的自校准方法[14]。该方法所需的互扫描靶制作复杂,且当测量网络中增加新的测量单元时,该方法并不具备自动组网的功能。本文提出了一种新的分布式测量系统自动标定方法。该方法在每个测量单元局部坐标系上固定已知坐标的两个测量点形成标记靶,测量单元之间通过相互测量标记靶自动标定了测量单元之间的坐标系。相比于传统的方法,该方法无需花费大量时间成本去布置控制点或在多个位置摆放标准器,大大提高了分布式测量系统的应用效率,本文方法降低了现有自动标定模型复杂的安装工艺,且能在测量网络中测量单元移站或者增加测量单元时,使得所有测量单元自动组网。
1 自动标定方法
基于标准器的标定方法是一种常用的坐标统一化方法。标准器由碳纤维等温度系数较小且几何结构稳定的材料制成。在标准器上布置目标点,并利用高精度的方法标定出各目标点之间的几何关系,包括距离信息和角度信息。将这些几何关系作为现场测量的约定真值。现场标定时,由测量仪器测量标准器上目标点坐标。根据目标点的几何关系建立约束,以统一测量仪器的坐标系。
在标准器上布置的目标点越多,结构越稳定,测量越准确。但是过多的约束点会降低测量效率,增大加工难度。为了不产生形变,通常标准器的尺寸不能设计的过大。标准器上目标点之间的最大距离通常在几百毫米内。以这样的方式建立约束,只能保证标准器周围测量空间的准确性。因此,需要在测量空间内人为移动标准器到不同位置进行测量,以覆盖整个测量空间。大空间定位系统的应用场合通常测量范围大,精度要求高,且测量环境复杂。为了适应测量任务,标准器移动的位置越多,标定的精度越高。而每一次移动标准器必定增加标定的时间成本,以牺牲效率为代价来获取较高的精度。
为提高标定效率,在每个测量单元的自身坐标系上固定两个测量节点作为标记靶。每个标记靶上测量点的坐标值在测量单元自身坐标系下固定不变。在实际使用时,测量单元之间通过相互测量彼此的标记靶获得测量点在不同坐标系下的坐标值,利用这些测量点在不同坐标系下的坐标值建立三维约束,从而自动的标定了不同坐标系之间的坐标转换关系。为清晰的阐述这一自动标定的过程,将第i号测量单元的坐标系定义为CS-i。同时,将第i号测量单元标记靶上的第k(k=1,2)个标记点在CS-i中表示为而第j号测量单元测量该标记点在坐标系CS-j的坐标为,如图1 所示。

图1 测量单元相互测量示意图Fig.1 Schematic diagram of measurement units measuring each other
测量网络中4 个标记点的三维坐标在CS-i和CS-j坐标系建立线性关系
式中,Rij、Tij为CS-i到CS-j的旋转平移矩阵,包含12 个待求解的未知参数。将式(1)在X、Y、Z三个方向上分解为关于Rij和Tij的n×3 个线性方程,并将式(1)变化为
在实际应用中,如果式(3)中的ATA矩阵接近奇异矩阵,那么会出现系数矩阵病态问题[15],从而导致式(3)中解得的X较大程度的偏离实际值。而保证ATA矩阵不奇异的前提条件是组成A矩阵的四个点在空间中不共面。令两个标记靶上的四个点在空间中不共面后,那么该方法将能通过测量单元之间相互测量彼此的标记靶从而自动标定不同测量单元之间的坐标系。
与传统的控制点和标准器的标定方法相比,该方法无需花费人工成本去布置控制点或摆放标准器,极大的缩减了标定时间。并且在测量单元移站或者在原有的测量网络中添加新的测量单元时,该方法天然的可以实现测量单元的自动组网,无需对测量场重新进行标定,提高了分布式测量系统的应用效率。
2 基于ALPS 的全自动标定方法
2.1 ALPS 测量原理
精密激光定位系统ALPS 是一种典型的分布式测量系统,主要由激光发射站、光电接收器、信号处理器、以及上位机组成,如图2 所示。工作时,发射站向测量区域发出两束扫描激光平面,多个发射站的激光平面交会于接收器,经过信号处理和计算实现三维坐标测量[16]。

图2 ALPS 系统的组成Fig.2 The composition of the ALPS system
ALPS 中单台激光发射站可以抽象成两个互成一定角度的光平面和一个转轴的数学模型。在初始时刻,扫描光平面的单位法向量可以用[a1b1c1d1]T和[a2b2c2d2]T表示。这些参数在激光器安装好后就固定不变,称为发射站的内参数,可通过标定获得[17-19]。
假设初始时刻的扫描光平面[ai bi ci di]T在发射站旋转过角度θi时扫过测量节点,则扫描光平面此时的平面方程可通过初始时刻的单位法向量绕Z轴旋转得到,即
单台发射站可以确定两个方程,若测量空间中发射站数量多于一个时,根据交汇测量原理,就可实现坐标值的测量,如图3 所示,两个发射站的扫描光光平面在空间中交汇于一点。

图3 双站交汇测量示意图Fig.3 Two-station intersection measurement diagram
而在有多个激光发射站的测量场中,以n表示发射站的总数,将所有扫描光平面统一到公共坐标系,根据式(5),测量节点的坐标与这些平面方程的联立约束可以表示为
当光平面方程数大于未知参数个数时(n>1 时),方程有解;此方程组可以写为AX=B的形式,其最小二乘解为
2.2 标记靶的标定
第1 节阐述的分布式测量系统自动标定方法的基础是标记靶在其测量单元自身坐标系下的坐标标定,本节以Q111的获取为例阐述标记靶上的传感器在测量单元自身坐标系下坐标标定的整个过程。首先在实验室中布置三台及以上的发射站并在每台发射站上固定好标记靶后,通过现有的高精度标定方法(如标准尺法)求解这些发射站坐标系之间的转换关系[10,15]。如图4 所示,定义发射站i到发射站k的旋转平移矩阵分别为Rik、Tik。

图4 标记靶标定示意图Fig.4 Schematic for calibrating the mark targets
式中,m=1,2,表示激光平面的序号;分别为发射站2、发射站3 的激光平面m绕自身坐标系z轴旋转扫描到时的旋转矩阵;n2m,n3m分别表示发射站2,3 的激光平面m在初始时刻的光平面系数;表示在发射站j坐标系下的坐标;同时与满足
联立式(8)、(9)即可推出
式(10)由4 个平面方程组成(m=1,2),Rij,Tij分别为利用标准尺法事先标定的发射站i坐标系到发射站j坐标系的旋转矩阵和平移矩阵,式中未知数只包含的坐标值。解得后同理可解得其他标记靶在其基发射站下的坐标
2.3 ALPS 标定模型
本节以求取j号激光发射站标记靶上的测量点和
在i号激光发射站坐标系下的坐标为例,阐述两个发射站坐标系之间的标定过程。记在CS-i(i号激光发射站坐标系)的坐标分别为和i号激光发射站测量和时,两个激光扇面分别交汇成一条由CS-i坐标原点指向和的射线r1、r2。通过r1、r2的射线方程可得两射线的俯仰角分别为β1、β2,射线之间的夹角为在CS-i的XOY面投影点记为Pk。点的延长线与CS-i的XOY面相交于点P3,该延长线与CS-i的XOY面的夹角为β4。如图5 所示。
上述几何关系中P1、P2和P3位于同一直线,则和相似,满足几何关系
综上,联立式(11)、(12)、(13)、(14)得到
通过式(15)解得
式中a=(sinβ1-sinβ2)2,b=2Lsinβ1sinβ4(sinβ2cosβ3-sinβ1),c=L2sin2β1(sin2β4-sin2β2);L是两点之间的欧式距离。另外,为保证ALPS 中激光发射机平稳运行,发射机在制造时会借助现场动平衡仪进行严格的调平。并且在扫描激光面的参数标定时,会以平行于地面的平面建立发射站自身坐标系的XOY面,因此CS-i和CS-j的XOY面几乎都与地面平行。这一特性使得β4(点所在的直线与CS-i的XOY面的夹角)等于直线与CS-j中XOY面的夹角。即β4可以通过提前标定的坐标求得,从而利用式(16)解得了两组再将射线rk(k=1,2)写成参数方程的形式
2.4 ALPS 标定参数的优化
在获得ALPS 中发射站坐标系统一关系的估计值后,为进一步获得更高精度的坐标统一关系,引入发射站相互扫描的点面约束、旋转矩阵的正交约束以及标记靶上光电接收器之间的距离约束建立优化模型。总体示意图如图6 所示。

图6 发射站互扫描测量示意图Fig.6 Schematic diagram of mutual scan measurement at transmitter station
当第i号发射站标记靶上的k号光电接收器接收到j号发射站的扫描激光时,根据式(6),相关激光平面约束方程为
式中,Rij,Tij分别表示CS-i到CS-j的旋转矩阵和平移矩阵,为待优化参数,m代表了发射机扫描激光面的编号。另外,利用事先标定的与两台激光发射站互扫描得到的利用它们之间的差值构建距离约束
此外,当旋转矩阵表示为式(20)的形式,其正交约束如式(21)
式中,s(s=1,2,…,6)代表了相应方程的编号,c代表了不同矩阵的编号;将以上约束联立,得到非线性最小二乘法表示的目标函数
式中,N为发射站的总台数;i、j为发射站的序号,发射站不能扫描到自身的标记靶,故i≠j;c表示旋转矩阵的序号;fsc表示第c个旋转矩阵满足的正交约束方程;M1,M2为惩罚因子。式(22)是一个经典的非线性最小二乘方程组的优化问题,针对这类问题目前常用的方法包括梯度法,高斯牛顿法以及Levenberg-Marquardt(LM)算法[20-21]等。LM 算法可以自适应的调整步长,兼具高斯牛顿法和梯度法的优点,可以有效减少函数陷入局部极值的几率,被广泛应用于大尺寸测量系统的标定[10-14]。因此,将2.2 节的结果作为LM 迭代初值,式(22)作为目标函数即可解得更精确的坐标统一化参数。
3 实验验证
本文提出的标定方法依托于ALPS 进行原理验证。首先在5.5 m×5.5 m 的空间中布置两台相互可以测量到标记点的激光发射站。然后将标记靶固定在激光发射站周围,如图7 所示。发射站距离地面高度约为1.5 m。算法涉及的激光平面参数预先标定,结果如表1 所示。标记靶上的测量点在基发射站坐标系下的坐标利用标准尺法标定[10,14],结果如表2 所示。

表1 激光发射站的内参数Table 1 Internal parameters of laser transmitters

表2 发射站上扫描靶坐标Table 2 Scan the target coordinates at the laser transmitters
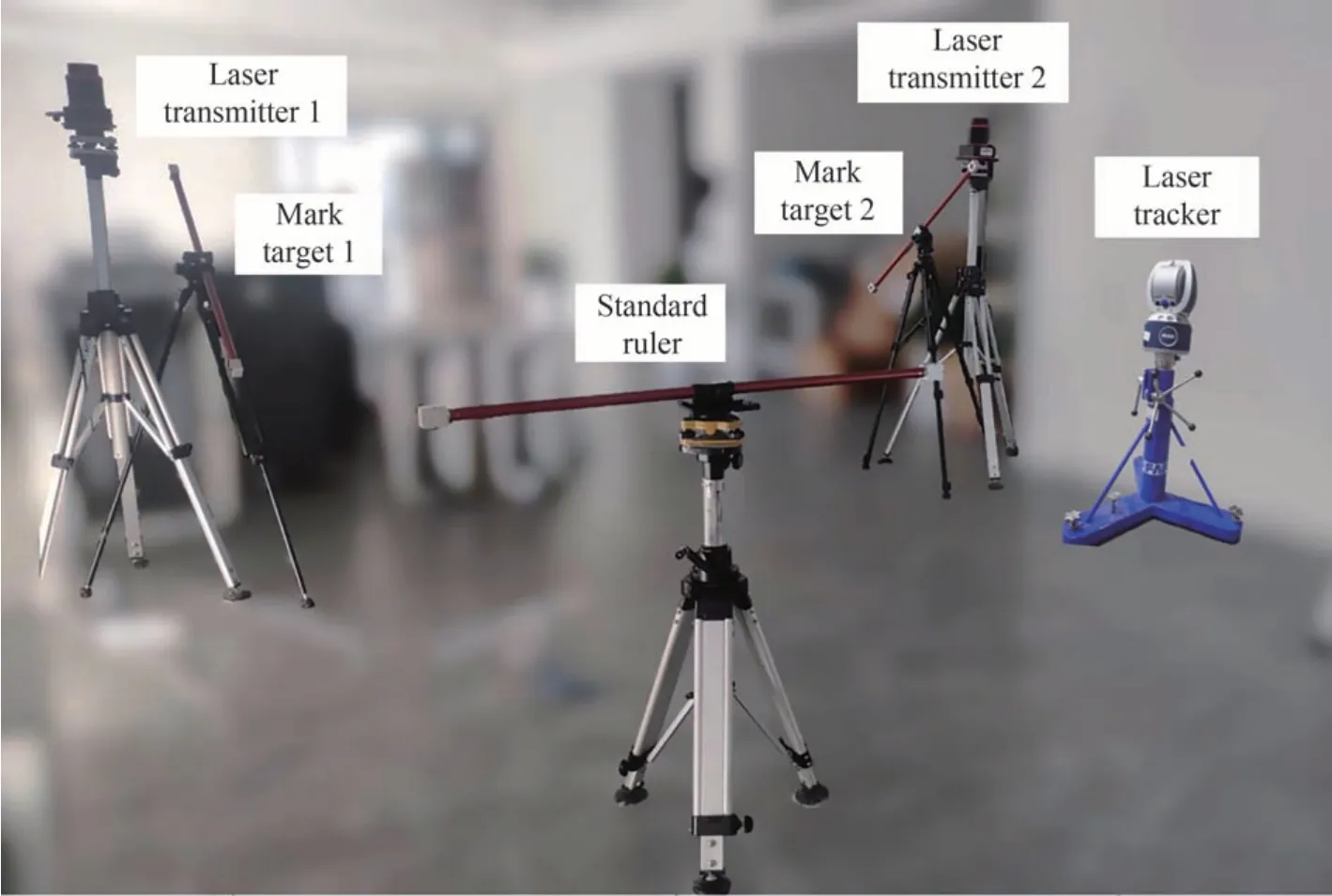
图7 实验场景Fig.7 Experimental scene
3.1 测距实验
为了评估该方法的标定精度,分别使用基于标准尺的标定方法和本文提出的方法对测量场标定。在距离发射站布站区域约2 m,大小为5 000 mm×5 000 mm×500 mm 的测量空间中12 个不同位置,依次测量标准尺(1 156.704 mm)。记录测量结果相对于其基准长度的偏差,如图8 所示。此外,本节分别利用LM 算法与高斯牛顿迭代法对同一标定初值进行了优化。并基于标定初值以及两种算法优化后的标定结果,计算了空间中12 个不同位置上的标准尺的测距误差,突出了LM 优化算法在大尺寸测量系统标定问题上的优越性,结果如图9 所示。

图8 与标准器法相比的长度测量误差比较Fig.8 Comparison diagram of length measurement error compared with standard method

图9 LM 优化法与高斯牛顿优化法比较Fig.9 Comparison diagram of LM optimization method and Gaussian Newton optimization method
图8 表明,利用本文方法对测量场标定后,1 156.704 mm 的标准杆其距离测量误差在0.46 mm/m 之内。该方法虽然比标准器法的精度略有下降,但将标准器法繁琐的标定过程变为了自动标定,降低了人工成本,其测量精度仍能满足大部分工业测量的需求[22]。尤其面对测量网络中原有测量单元移站或者增加测量单元的情况时,该方法天然的可以实现测量单元的自动组网,无需对测量场重新进行标定,提高了大尺寸测量系统的应用效率。此外,图9 表明,LM 算法以及高斯牛顿迭代法都可以优化标定初值,提高大尺寸测量系统的标定精度。但是LM 算法自适应步长的特点使得其比高斯牛顿法的优化效果更好,在大尺寸测量系统的标定问题上得到了普遍的应用[10-14]。
3.2 测点实验
为了进行更全面的验证,本节实验借助如图10 所示的靶球完成了ALPS 与激光跟踪仪系统的测点对比试验。实验中所用靶球通过机械设计,使得激光跟踪仪与ALPS 测量的物理中心点重合,即靶球可以作为激光跟踪仪与ALPS 测量的公共点。在实验之前通过ALPS 与激光跟踪仪分别测量靶球在30 个不同位置的坐标,然后通过这30 个公共点分别在ALPS 与激光跟踪仪坐标系下的坐标值,借助式(2)、式(3)完成激光跟踪仪与ALPS 坐标系的统一。

图10 靶球实物Fig.10 Illustration of the target ball
获得激光跟踪仪与ALPS 的坐标系统一参数之后,在5 000 mm×5 000 mm×400 mm 的空间内随机分布10 个靶球作为测量点,如图11 所示。利用ALPS系统对每个点的坐标重复测量500 次,计算不同点坐标重复测量的标准偏差,结果如图12 所示。然后利用激光跟踪仪设备测量这些点的三维坐标。由于跟踪仪具有极高的测量精度,因此将激光跟踪仪对每个点的坐标测量值作为真实值。将每个点的坐标500 次重复测量的平均值作为测量值,比较测量值与真实值之间的偏差,结果如图13 所示。

图11 测量点分布Fig.11 Test point distribution map

图12 重复测点标准差Fig.12 Repeat point standard deviation

图13 与激光跟踪仪相比的测量误差Fig.13 Measurement error compared with laser tracker
实验结果表明,利用本文方法对测量场完成坐标统一化后。坐标测量在x、y、z的标准差分别在0.026 mm、0.024 mm、0.023 mm 之内。与激光跟踪仪相比,坐标测量在x、y、z方向的最大误差分别为0.5 mm、0.55 mm、0.5 mm。总体而言,利用本文方法标定后的测量场具有良好的稳定性。绝大部分工业测量的精度一般为±2 mm[22],本文方法在坐标测量时最大误差也可以满足大部分工业测量的需求。
3.3 分析与讨论
基于标准器的标定方法广泛应用于大尺寸测量系统的坐标系标定问题[13-14],标准器一般由碳纤维等温度系数较小且几何结构稳定的材料制成。在标准器上布置目标点,并利用高精度的仪器测量出各目标点之间的几何关系,包括距离信息和角度信息。将这些几何关系作为现场测量的约定真值。现场标定时,由待标定测量单元测量标准器上目标点坐标,根据目标点的几何关系建立约束,以统一各个测量单元的坐标系。文献[10]提出的标准器标定方法尽管它可以使得大尺寸测量系统实现令人满意的精度,但校准过程必须至少捕获标准尺的六个垂直姿态,才能计算标定算法的初始值,再利用LM 算法迭代求解。而每一次移动标准器且调整垂直必定增加标定的时间成本。本文方法通过两个测量单元相互测量标记靶,即可自动获取坐标系统一的初值,最后利用LM 算法迭代求解即可获得更为准确的坐标系标定参数。本文提出的标定方法的时间成本主要来源于LM 算法的运行时间,避免了在测量现场人为移动调整标准尺的工作,从而大大减小了标定过程的时间成本。两种方法的标定效率对比如表3 所示。

表3 标准尺法和本文的方法的比较Table 3 Comparison of the standard ruler method and the method in this paper
表3 表明,利用本文提出的标定方法对测量场标定后,长度测量误差在0.46 mm/m 内,与基于标准尺的标定方法相比测距误差略有下降。与之不同的是使用标准尺的传统标定过程大约需要一个小时,而使用本文提出的方法在五分钟内即可完成。因此,该方法显著提高了标定效率,且仍可以满足大部分工业测量±2 mm的精度需求[22]。
为了提高大尺寸测量系统的坐标系标定效率,吴军等[14]创造性的提出了一种自标定方法。该方法需要在测量单元上安装三个测量节点和一个超声波测距模块形成互扫描靶,如图14 所示。
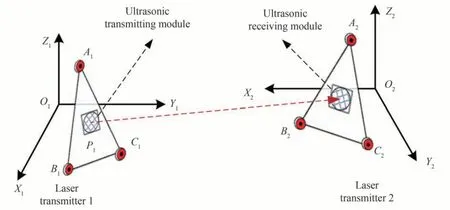
图14 基于超声波测距的互扫描自动标定方法示意图Fig.14 Self-calibration method using inter-scanning technique and ultrasonic ranging
基于超声波测距的自标定方法在工作时首先需要1 号发射站扫描靶中的超声波发送模块发出声波信号,2 号发射站扫描靶的超声波接收模块获得声波信号后根据时间差以及声音的传播速度计算两个扫描靶之间的距离。最后借助该距离以及两台发射站相互测量扫描靶的信息获取坐标系标定算法的初始值。为了更大的测量范围以及更高的测量精度,在实际的测量场中发射站的数量往往多于两台。文献[14]提出的自标定方法在应对多台发射站需要标定时,选择哪些发射站发射超声波哪些发射站接收超声波是一个需要研究解决的问题。即使每台发射站都装有超声波发送接收模块,在多个声波源同时工作时,超声波的接收模块甄别出声波的来源是计算任意两个扫描靶之间的距离的前提,这一前提仍是文献[14]提出的自标定方法在实际应用中的重要制约因素之一。而本文提出的方法,天然的可以实现任意两台发射站的自动标定,且标记靶制造工艺简单,有望实现具有自标定功能的大尺寸测量系统的产品化。
4 结论
为了提高分布式测量系统的坐标统一化效率,本文提出了一种基于测量单元相互测量的坐标统一化方法。该方法通过固定两个在测量单元局部坐标系已知坐标的测量节点作为标记靶,测量单元之间相互测量标记靶,结合提前标定的标记靶在自身测量单元坐标系下的坐标,即可自动的标定任意两台测量单元的局部坐标系。本文方法显著提高了校准效率,与现有的自动标定模型相比,本文方法降低了扫描靶复杂的安装工艺,有望为具有自动标定功能的分布式测量设备的产品化提供新的理论基础;另一方面,当测量单元移站或者原有的测量网络中添加新的测量单元时,本文方法可以实现测量单元之间的自动组网,无需对测量场重新进行标定,提高了分布式测量系统的应用效率。

