基于集体离群点挖掘的电网潜在故障检测算法

黄晓地　吴淑慧　陈诚　胡中峰

摘要：针对城市电网故障早期阶段的隐蔽性、潜伏性特点，通过构建“集体离群点-故障模式”的度量规则，对电网系统中全等级异常电流波动信号进行层次聚类分析，将区域性潜在故障检测问题转换为挖掘故障信号数据中的集体离群点问题。为提高检测效率，设计了一种基于不动点迭代法的层次聚类改进算法（Fixed point iteration based k-medoids， FPK-medoids），利用不动点较强的局部搜索能力提高聚类收敛速度。在测试数据集和实例数据集上进行实验，结果表明改进算法的收敛性能优于传统算法，检测模型能够精准识别电网中的区域性潜在故障。

关键词：潜在故障；集体离群点；不动点；层次聚类；FPK-medoids算法

中图分类号：TP391.4文献标志码：A文章编号：1001-2443（2024）01-0011-09

随着城市化进程加快，以居民、金融工商业、服务业、高端制造业为代表的城镇负荷增加迅猛，智能化是城市电网发展的必然趋势和方向，也是解决城市电网所面临问题的有效途径［1］。

现有研究主要从布局规划和故障应急两方面提高城市电网的稳定性［2］。基于布局规划的研究，根据城市最大供电能力、电力需求曲线以及电网运行方式，多采用层次分析法［3］，包络分析法［4］，群智能仿生算法［5］等多目标规划的全局寻优算法对不同能级的电网进行合理配置，避免因交直流并行，电力载荷不均匀，以及次联故障等对电网稳定性的影响。力求在电网的布局设计阶段，最大程度消除非外力干扰下电网自身运行过程中可能出现的不稳定因素。如自愈控制体系［6］，电网柔性分区互联［7］，以及建立保底电网等［8］。

合理的电力调度能够提高城市电网的灵活性，但故障诱因复杂多变且具有显著的不确定性，因此在无法完全预测的情况下制定健全的故障应急机制是电网鲁棒性的关键保障［9］。故障应急一般分为故障识别和处理决策，故障识别是关键，行动决策是基于前者提供的信息做出的最优化抉择［10］。目前，基于城市电网的故障识别主要有以下几种途径。基于专家系统的检测途径，通过构建模式识别知识库和故障原因推理机，提高故障检测的效率［11］。基于信号处理的检测途径，通过对电路中的信号进行降噪、放大、叠加等处理，根据信号特征的异常变化幅度和趋势识别可能出现的故障［12］。基于信息融合的检测，通过对城市电网中产生的各种多源、异构、不完备信息进行融合，提高城市电网系统对不确定信息的处理能力和对报警信息的充分利用［13］。基于数据驱动的检测，通过分析故障数据和正常数据，挖掘不同影响因素之间的强相关规律，提高检测的效率［14］。

此类针对电路参数超出额定范围或直接引起继电器跳闸的故障信号检测，虽然可以明显提高城市电网鲁棒性，但多属于反馈控制机制［15］。城市电网中占据较大比例的仍是潜在性故障，即从异常征兆出现到完全爆发之间存在一定的时间间隔的电网故障类型。早期阶段，潜在性故障引发的电路信号偏差幅度较小，无法通过单点的阈值检测识别，而是需要对一定范围内对所有电路信号的变化幅度进行综合分析。如果能精准识别潜在性故障的早期异常特征，则有助于延长应急时间，降低故障造成的损失和辐射影响

本文提出一种基于集体离群点挖掘的电网区域性潜在故障检测算法。首先构建“集体离群点—潜在性故障”的度量规则，将故障识别问题转换为集体离群点挖掘问题。其次，设计一种基于不动点迭代法的改进聚类算法 （Fixed point iteration based k-medoids， FPK-medoids），对检测范围内接收到的所有电路异常波动信息进行层次聚类。最后，对比同层聚类簇和上下层聚类簇之间的簇内信息，识别由集体离群点表征的电网区域性潜在故障，并据此确定故障源位置和检修路径。

1 不动点理论

1.1 不动点定义与定理

定义1 设f为n维欧式空间Rn的自映射，若存在x*∈Rn，满足f（x*） =x*，则称自变量x*为映射f的一个精确不动点。

定义2 设设f为n维欧式空间Rn的自映射，ε为任意正数，|x-f（x）|为n维欧式空间Rn的中向量x-f（x）的模。若存在自变量x*满足|x-f（x）|<ε，则称x*为映射f的一个近似不动点。

定义3 设f是n维欧式空间Rn的自映射，对于任意自变量x=（x1，…， xn）∈Rn，其映射函数f（x）=f（x1，…，xn）可表示为：f（x1， …， xn）=（f1（x1，…，xn）， …， fn（x1，…， xn））。

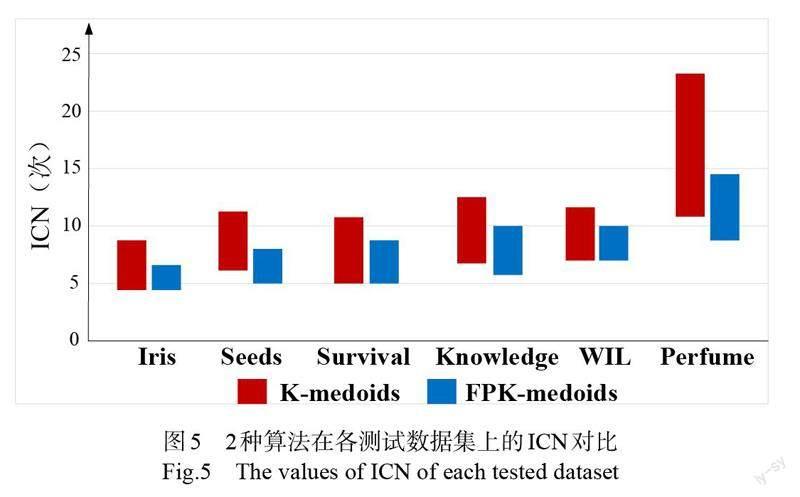
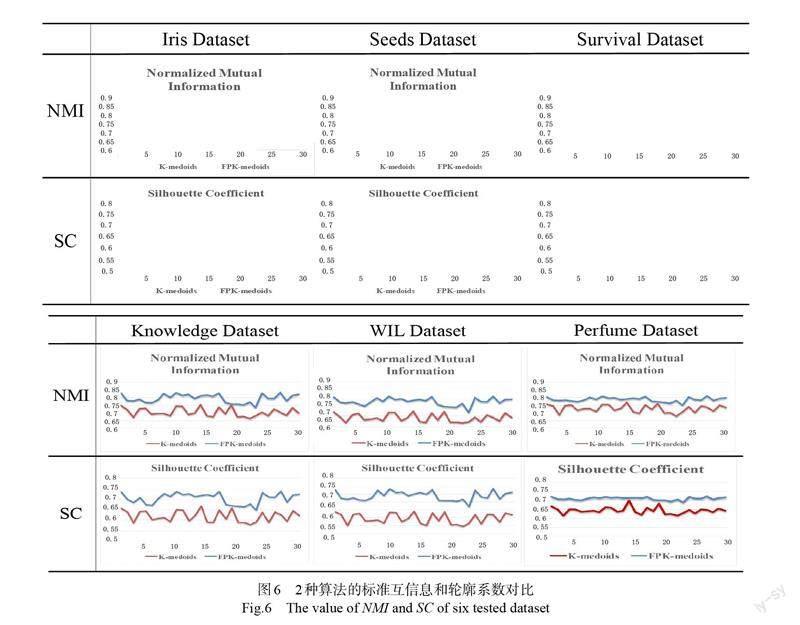
定理1 在有界非空集合X内，对于任意映射f，在定义域［a，b］内，若满足以下条件：（1）对任意自变量x∈X，满足a≤T（x）≤b；（2）存在正常数L<1，对任意自变量x，y∈X，均满足|T（x）- T（y）|<

1.2 不动点方程

不动点方程是应用数学领域解存在性、唯一性证明以及求解策略分析的有力工具［16］。本文通过将目标函数极值求解问题转换为不动点方程求解问题，利用不动点迭代法在解空间内搜索最优解。函数最极值求解问题按公式1描述。

其中f（X）为目标函数，X为n维度优化变量，gi（X） 为极值求解问题的m个约束函数。若目標函数在定义域内处处可导，则函数的极值必然出现在满足导函数f'（X）=0的位置；反之，满足导函数f'（X）=0的点可能是极值、拐点等。通过构建不动点方程，先筛选出f'（X）=0的点，再通过目标函数判断最优解，可极大程度降低极值求解的搜索空间。具体步骤如下：

（1）构建不动点方程：F（X）=X- f'（X）。根据定义1，若F（X）存在不动点X*，则必然满足F（X*）=X*- f'（X*）=X*，由此可得f'（X*）=0。

（2）根据定义3，函数f（X）=f（x1，…，xn）可表示为（f1（x1，…，xn）， …， fn（x1，…， xn））。按公式2将其转换为不动点方程组，通过求解不动点方程组寻找函数极值。

（3）在解空间内寻找出所有满足F（x）=x- f （x）的精确不动点或近似不动点形成候选集，进而通过目标函数从中选择最优解。

1.3 不动点迭代法

不动點迭代法的基本思想是通过逐次逼近法将隐式方程归结为一组显式方程。若不动点方程满足定理1，则基于不动点迭代法的求解过程为：

（1）将方程f（x）=0改写成x=φ（x）形式；

（2）在方程的解空间内随机选择初始近似解x0带入x=φ（x）右端，得到x1=φ（x0）；按迭代式：xk+1=φ（xk），k=0，1，2…，在解空间内迭代计算；

（3）在达到预设最大迭代次数前，若找到点x*，满足x*=φ（x*），x*即为方程f（x）的精确不动点。若未找到精确不动点，则按定义2寻找满足|x-f（x）|<ε，且精度最大的近似不动点作为近似解，视其满足f（x*）=0。

2 检测模型

2.1 基于集体离群点的故障度量

城市电网中产生的三相电流信号按波动程度可为五个等级，如图1所示。波动等级在Level 1-2以内的信号通常会被忽略，视为电网正常波动；Level 3-4范围内的波动信号如果在下一个采集时刻恢复，则将标记释放掉。只有Level 5的异常信号会被立即处理，这类后反馈的阈值监测方式往往只能在激变期内发现即将出现的电网故障。

为尽早识别城市电网中可能存在的潜在性故障，本文通过构建“集体离群点—潜在性故障”的度量规则，将潜在性故障检测问题转换为挖掘电网波动信号数据中是否存在集体离群点。集体离群点通常是由一系列相关数据实例组成，当它们以某种模式共同出现时，其整体表现方式明显偏离数据流的正常期望，但每个数据实例单独分析时不构成离群点［17］。本文将城市电网中出现的波动信号均视为正常的数据实例，但如果在某基站覆盖范围内出现大量波动信号，则将这些波动信号判定为集体离群点。

2.2 模型框架

检测模型分为两阶段，如图2所示，首先以FPK-medoids聚类算法逐层抽离波动信号数据的概要信息；其次，根据同层和跨层聚类簇的簇内信息对比，挖掘由集体离群点表征的潜在性故障。

2.2.1 层次聚类 电网中不同能级的基站覆盖范围不同且相互重叠，线路结构复杂，远距离或跨区输电现象普遍。如图3所示， 一级变电站（TS）下并行存在TS·A，TS·B，和TS·C三个次级基站，次级基站下又存在多个子基站。

针对多能级电网中的故障源识别与定位问题，以出现波动信号的电路所隶属的上游基站（变电站）信息为度量，对接收到的波动信号进行层次聚类，以结构树的方式呈现出异常信号与各能级基站之间的关联关系。如图2所示，聚类层级对应不同能级的基站，从上至下依次细化。每一层的聚类簇，表示该基站范围内检测到的电流波动信号数量，颜色越深，表示波动信号数量越多。

2.2.2 故障判断规则 在多能级电网中，若上游基站出现故障，则下游基站覆盖范围内必然出现故障；反之，上游基站不会丧失全部功能。因此，基于多层聚类结果，首先对比所有聚类簇的簇内信息，检测是否存在集体离群点；其次对比上下层簇的簇内信息，确定造成电网区域性故障的源基站和溯源路径。主要判定规则和逻辑顺序可分为以下三步进行：

（1）基于聚类簇簇内密度度量的判断规则。以图2为例，颜色深浅反映故障程度，基站C1的下属基站C11，c111， 基站C2及其下属基站C21，c211，c212，基站C3及其下属基站C31，C32内的波动信号数量均超过正常范围，因此可以假定这些基站覆盖范围内的电路中可能存在集体离群点。

（2）基于不同层聚类簇簇内互信息（MI）对比的判断规则。以图2为例，对其中出现的3种情况进行分别讨论：首先，在基站C3覆盖的网路中，MI（C3， C31）与MI（C3， C32）相似，且C31与C32内均疑似出现离群点，则基站C3为故障源的概率最大。其次，在基站C2覆盖的网路中，由于MI（C2， C21）与MI（C2， C22）不相似，则故障源可能在下级基站，基站C21内又疑似出现集体离群点，则基站C21为故障源的概率最大。继续对比基站C21与其下属基站的簇内信息，MI（C21， c211）与MI（C21， c212）相似，进一步佐证基站C21为故障源。最后，在基站C1覆盖的网路中，MI（C1， C11）与MI（C1， C21）不相似，且基站C11中存在集体离群点，则基站C11为故障源概率最大。继续对比C11与其下属基站的簇内信息，MI（C11， c111）与MI（C11， c121）不相似，但MI（C11， c111）的值更大，且基站c111内也存在集体离群点，因此基站c111为故障源概率最大。

（3）基于故障聚类簇异常波动的平均程度来确定溯源路径。在第二步基础上，通过比较C3，C21，c111三个聚类簇的平均异常波动程度，判断故障的严重程度，并据此确定处理决策的优先级。

3 算法设计

在层次聚类过程中，本文设计一种基于不动点迭代法的FPK-medoids改进聚类算法。相较于以均值作为簇中心的聚类算法，如k-means算法等，选择真实的波动信号作为中心点在故障源定位等方面更有实际意义，还可以有效降低对极值、噪声或缺失值的敏感性。在簇中心迭代阶段，引入不动点算法，利用其较强的局部搜索能力，并行加快同一层所有聚类簇的簇中心迭代收敛速度，进而提高故障检测的效率。

3.1 传统K-medoids算法

对于包含n个数据实例的数据集D，传统K-medoids算法主要采用围绕中心点划分的优化策略（Partitioning Around Medoids， PAM），通过最小化簇内数据间差异将数据集划分为预定义的k个聚类簇，使每个聚类簇最大程度满足簇内数据高度相似且簇间数据差异度最大。预定义聚类簇数k在[2：n]范围内按“肘方法”确定。按公式3，以绝对误差标准计算簇内数据差异度之和E。

其中oi为第i个聚类簇的簇中心，pj为聚类簇Ci中除簇中心以外的任意数据点，函数dist度量点pj到中心点oi的距离。

算法具体步骤为：

（1）从数据集中随机选取k个数据作为初始簇中心；

（2）将剩余的数据按照距离度量划分到与其最近的簇中心；

（3）计算各聚类簇绝对误差标准E；

传统算法中的PAM策略的優化过程：

（4）在数据集中，随机选择一个数据实例Orandom替代其所属聚类簇的簇中心；

（5）以新的簇中心进行聚类，计算新聚类结果的绝对误差标准E'；

（6）根据聚类质量估计簇中心的替换代价：?S= E′-E

（7）如果代价?S<0，则初始的簇中心被新簇中心替代，形成新的k个中心点；否则，保留原初始簇中心；

（8）对于每个初始簇中心，重复4-7步骤，直至聚类质量稳定。

3.2 FPK-medoids算法

每一个替换簇中心形成的新聚类簇，可视为有界离散非空集合，由不动点定理1可知，这样的集合必定存在唯一不动点。因此，FPK-medoids算法以公式3中的绝对误差标准度量E为目标函数，构建不动点方程，将目标函数的极值求解问题转换为不动点方程求解问题。算法结构如图4所示，具体步骤如下：

（1）从数据集中随机选取k个数据作为初始簇中心；

（2）将剩余的数据按照距离度量划分到与其最近的簇中心；

（3）计算各聚类簇绝对误差标准E；

基于不动点迭代法的簇中心优化选择过程：

（4）对于每个聚类簇Ci，以绝对误差标准E为目标函数，构建不动点方程E'=0。将搜索目标函数极小值的问题转换为不动点方程求解问题；

（5）将不动点方程E'=0改写为x=φ（x），以每个初始簇中心为初始值进行不动点迭代，在各个聚类簇范围内的数据中搜索不动点o*；

（6）如果在达到预设最大迭代次数前，若找到点o*，满足o*=φ（o*），则o*即为不动点方程E'=0的精确不动点。若未找到精确不动点，则根据定义3寻找满足| o*-φ（o*）|<ε且精度最大的近似不动点作为解，视其满足E'=0。

（7）以搜索到的不动点作为新簇中心进行聚类，形成新的k个聚类簇Ci'；

（8）对比每个新聚类簇与前一轮聚类簇的质量si=E（Ci'）?E（Ci），如果绝对误差标准的数值降低（即si≤0），则以不动点作为新的簇中心；若绝对误差标准的数值升高（即si>0），则保留前一轮的簇中心；

（9）基于第8步得到的新簇中心进行聚类，对聚类结果按2-8步进行优化，直至所有聚类簇的质量不在发生变化或算法达到预设迭代次数。

在重定位过程中，传统K-medoids算法的复杂度为（k（n-k）2），其中k为聚类簇数，n为数据集规模。FPK-medoids算法在该过程中可以并行的在所有聚类簇中进行簇中心迭代优化，既保留了原算法的鲁棒性又提高了聚类效率，复杂度按公式4计算。

3.3 算法测试

3.3.1 测试数据集 本文选取六个UCI实际数据集（数据库链接：http：//archive.ics.uci.edu/ml/datasets.php），分别用传统K-medoids和FPK-medoids算法进行30次实验，记录各项度量指标的最大值，最小值与均值，并绘制成曲线图。数据集详细信息见表1所列，聚类前已对所有数据集进行归一化预处理。

3.3.2 聚类质量评价指标

（1）轮廓系数 （Silhouette Coefficient， SC）。通过计算数据集中所有对象的轮廓系数平均值，对聚类结果进行评价。取值越接近1，则聚类结果合理；取值接近-1，则聚类结果不合理。

（2）标准互信息（Normalized Mutual Information， NMI）。通过对比数据集的实际标签分布和聚类后的分布，对聚类结果进行评价。合理聚类结果的标准互信息的取值范围NMI∈［0，1］，取值越大，聚类结果与真实情况越吻合。

（3）迭代收敛次数（Iterative convergence number， ICN）。预设最大迭代次数为50，迭代收敛次数反映聚类达到稳定时算法实际运行次数。

3.3.3 测试结果 传统K-medoids和FPK-medoids两种算法在六个数据集上30次测试结果的平均值见表2和表3所列，所有数值均保留至小数点后3位。

3.3.4 测试分析 两种算法在六个数据集上的迭代收敛次数的对比如图5所示。FPK-medoids算法在Iris、Seeds、 Survival和Knowledge四个数据集上的聚类速度有明显提升；对于数据规模n较大的WIL数据集，聚类速度虽也有改进，但提升效果较前几个数据集而言相对较弱；对于期望聚类簇数k较大的Perfume数据集，由于算法复杂度从k（n-k）2下降为（n-k）2，聚类速度有非常显著的提高。

基于根据轮廓系数与标准互信息，K-medoids算法和FPK-medoids算法在六个数据集上的聚类质量对比如图6所示。对于Iris、Seeds、Knowledge和Survival四个数据集，FPK-medoids算法的聚类质量趋势明显优于K-medoids算法，且质量曲线更加平稳。对于数据规模n较大的WIL数据集，聚类质量的改善极为明显，效果提升幅度远大于其余数据集；但对于期望聚类簇数k较大的Perfume数据集，虽然聚类质量依然有所改进，但效果提升的幅度较前几个数据集而言相对较小。

4 实例测试

以合肥市蜀山区合肥盛大电力公司2021年6—8月收集的电网数据为基础，对本文提出的检测模型进行测试，实验在Python3-4.4.0版本，Intel i7、3.6 GHz、8Gb内存环境下实现。

4.1 测试数据

监测平台每分钟对采集到的三相电流数据进行一次分析，为了简化数据处理过程，本文也将分析的滑动时间窗口设置为1分钟。通过与正常电流浮动范围的比较，将实时采集到的三相电流数据转换成电流波动信号。如图7所示，用红色圆圈标记的8个点表示当前时间窗口中采集到的电流波动信号。基于1分钟长度的时间窗口，将连续采集到的各检测点的当前电流数据流转换成反应波动信号的时间序列数据流，采集时点为时间属性，信号波动为行为属性。

对其运维范围内城市电网于2021年6—8月期间实际发生的潜在性故障进行标记，与本文检测算法进行对比，具体信息见表4中所列。“潜在故障”是指从故障出现征兆到最终故障现象的形成之间有一段时间。

4.2 测试结果

检测过程的可视化示例如图8所示。图8a是T时刻基于本文提出的检测方法定位到某可能出现故障的基站范围内的异常波动信号的分析结果。虽然该区域内几乎没有高级别的异常波动信号，但聚集了大量level 1和level 2等级的波动信号，因此，算法将其识别为集体离群点，判断该基站覆盖范围内的电网可能出现了潜在性故障。图8b是在本文方法做出判断一个小时后，电网中产生的故障信号分布。可以看出，大量高危险信号出现，多处出现严重的电力故障，该区域现出明显的电力故障。

基于本文提出的多层聚类检测方法对6—8月份包河区电力运维数据进行集体离群点检测，识别出的潜在性故障标签见表5所列。

检测结果与实际故障标签的对比如图9所示。结果显示，除天气原因外，对由其它三种原因引发的潜在性故障检测率均达到90%以上。但总体而言，由天气引起的故障占故障总体比例很小，因此本文提出的检测方法在普遍情况下能够有效检测出城市电网中的潜在性故障。

5 结论

本文提出一种基于集体离群点挖掘的城市电网潜在性故障检测算法。算法测试表明FPK- medoids改进算法在高聚类速度和聚类质量方面明显优于对比算法。实例测试结果表明本文构建的检测模型，有能力识别出电网中潜在的和具有渐变性的故障，在早期阶段及时发现异常征兆，延长故障应急时间，避免或降低故障带来的影响，增强城市电网系统的稳定性和鲁棒性。

实验中发现由天气等自然灾害引起的故障往往波及到城市多个区域，通过分析更大范围的数据分析才能更好的反映其演变过程。此次测试仅基于包河区电力运维数据分析，故而识别率不高。下一步计划扩大测试数据规模，尤其是对城市不同区域的电网数据进行综合分析，验证检测模型和检测算法的有效性，并根据结果进行持续完善。

参考文献

［1］史云涛，赵丽平，林圣，等.城市电网中地铁杂散电流分布规律及影响因素分析［J］. 电网技术，2021， 45（5）： 1951-1957.

［2］何正友，李波，廖凯，等.新形态城市电网保护与控制关键技术［J］. 中国电机工程学报， 2020， 40（19）： 6193-6207.

［3］CHE Y B， JIA J J， ZHAO Y C， et al. Vulnerability assessment of urban power grid based on combination evaluation［J］. Safety Science， 2019， 113： 144-153.

［4］WANG C， JU P， WU F， et al. Long-term voltage stability-constrained coordinated scheduling for gas and power grids with uncertain wind power［J］. IEEE Transactions on Sustainable Energy， 2022， 13（1）： 363-377.

［5］REN M L， HUANG X D， ZHU X X， et al. Optimized PSO algorithm based on the simplicial algorithm of fixed point theory［J］. Applied Intelligence， 2020. 50（7）： 2009-2024.

［6］秦立軍，张国彦，陈晓东，等.含DG的智能配电网快速自愈技术研究［J］. 电测与仪表，2021， 58（7）： 67-73.

［7］鄂志君，张长志，杨帮宇，等.考虑能源互联的城市电网多能源协调调度方法研究［J］. 电力系统及其自动化学报， 2021， 33（1）： 8-12.

［8］胡鹏飞，朱乃璇，江道灼，等. 柔性互联智能配电网关键技术研究进展与展望［J］. 电力系统自动化， 2021， 45（8）： 1-12.

［9］宫宇，张莲，李涛，等.量子粒子群算法在配电网恢复重构中的应用［J］. 重庆理工大学学报（自科版）， 2022， 36（10）： 200-207.

［10］MAR A， PEREIRA P， MARTINS J F. A survey on power grid faults and their origins： A contribution to improving power grid resilience［J］. Energies， 2019， 12（24）： 4667.1-21.

［11］马子钦，廖凯，李波，等.含分布式电源和电动汽车的城市电网半不变量故障分析方法［J］.电网技术， 2021， 45（2）： 696-704.

［12］胡凯凡，茆美琴，何状，等.直流短路故障下基于暂态能量抑制的MMC-HVDC电网主电路电感参数优化［J］. 中国电机工程学报， 2022， 42（5）：1680-1690.

［13］王晴，刘友波，黄杨，等.考虑数据中心需求响应的城市电网阻塞管理［J］. 电网技术， 2020， 44（8）： 3129-3138.

［14］SHE B X， DONG Y Q， LIU Y L. Time delay of wide area damping control in urban power grid： Model-based analysis and data-driven compensation［J］. Frontiers In Energy Research， 2022， 10： 3389.1-11.

［15］姚卓磊，黄文焘，余墨多，等.智能配电网电力-通信灾害故障动态协调恢复方法［J］. 电力系统自动化， 2022， 46（19）： 87-94.

［16］MARASI， H R， AYDI H. Existence and uniqueness results for two-term nonlinear fractional differential equations via a fixed point technique［J］. Journal of Mathematics， 2021（1）： 1-7.

［17］CHATTERJEE A， AHMED B S. IoT anomaly detection methods and applications： A survey［J］. Internet of Things， 2022. 19： 1-22.

Potential Fault Detection Algorithm of Power Grid Based

on Collective Anomaly Mining

HUANG Xiao-di1，2， WU Shu-hui2， CHEN Cheng3， HU Zhong-feng1

（1. School of Economics and Management， Hefei University， Hefei 230601， China; 2. School of Management， Hefei University of Technology， Hefei 230009， China; 3. Anhui Electric Power Industry Association， Hefei 230001， China）

Abstract：In view of the latent and concealed characteristics of potential faults in the early stage of urban power grid， this paper proposed a novel detection approach based on hierarchical clustering. According to the measurement rule of “collective anomaly-fault pattern”， through clustering analysis on all levels of abnormal current fluctuation signals in the power system， the problem of regional potential fault detection is transformed into the detection of collective anomaly. Besides， an improved multi-layered clustering algorithm based on fixed point iteration （FPK-medoids） is designed to enhance the detection efficiency. The experimental results show that the convergence performance of the improved algorithm is better than the traditional algorithm， and the detection model can identify the regional potential faults in the early stage.

Key words：potential fault; collective anomaly; fixed point; hierarchical clustering; FPK-medoids algorithm

（責任编辑：马乃玉）

收稿日期： 2023-04-08

基金项目：教育部青年基金资助项目（21YJC630044）；安徽省高等学校人才基金资助项目（2022AH051774）.

作者简介：黄晓地（1989—），男，安徽合肥市人，博士，讲师，主要研究方向为数据挖掘、故障诊断、区块链技术.

引用格式：黄晓地，吴淑慧，陈诚，等.基于集体离群点挖掘的电网潜在故障检测算法［J］.安徽师范大学学报（自然科学版），2023，47（1）：11-19.