以问题为钥，开启小学数学深度教学之门

苏浙闽

［摘 要］问题驱动是深化数学教学的有效方法之一。在小学数学课堂教学中，教师优化课堂教学设计，巧妙提出问题，帮助学生打通数学与生活之间的通道，可为学生营造自主探究、深入学习的氛围，提升学生的数学素养。

［关键词］问题；圆；深度教学

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2024）05-0053-04

问题引导是一种以问题为核心，让学生在解决问题的过程中获得知识和技能的教学策略。实施问题引导教学策略时，教师不再是单纯的知识传授者，而是引导者和协助者，学生则从被动接受者变为主动探索者。这种教学策略有利于引导学生主动思考和分析问题，培养他们的批判性思考能力、逻辑推理能力及问题解决能力。

一、以问题开展深度教学的方案设计

小学数学深度教学的方案设计需遵循三项原则。第一，目的性原则。强调在教学过程中必须有明确的目标，教师应确保所教授的内容与设定的目标相符，使学生明确学习的意义和目的。第二，顺序性原则。内容的呈现和教学应按照一定的逻辑和顺序进行，从简单到复杂、从浅显到深入，使学生逐步加深对数学知识的理解。第三，适度性原则。在确定教学内容和难度时，需要考虑学生的实际能力和接受程度。过于简单的问题可能会让学生失去兴趣，难度过大的问题则可能会让他们产生挫败感，难度适当的问题可以体现“以生为本”的教学理念，并激发学生的兴趣和求知欲。

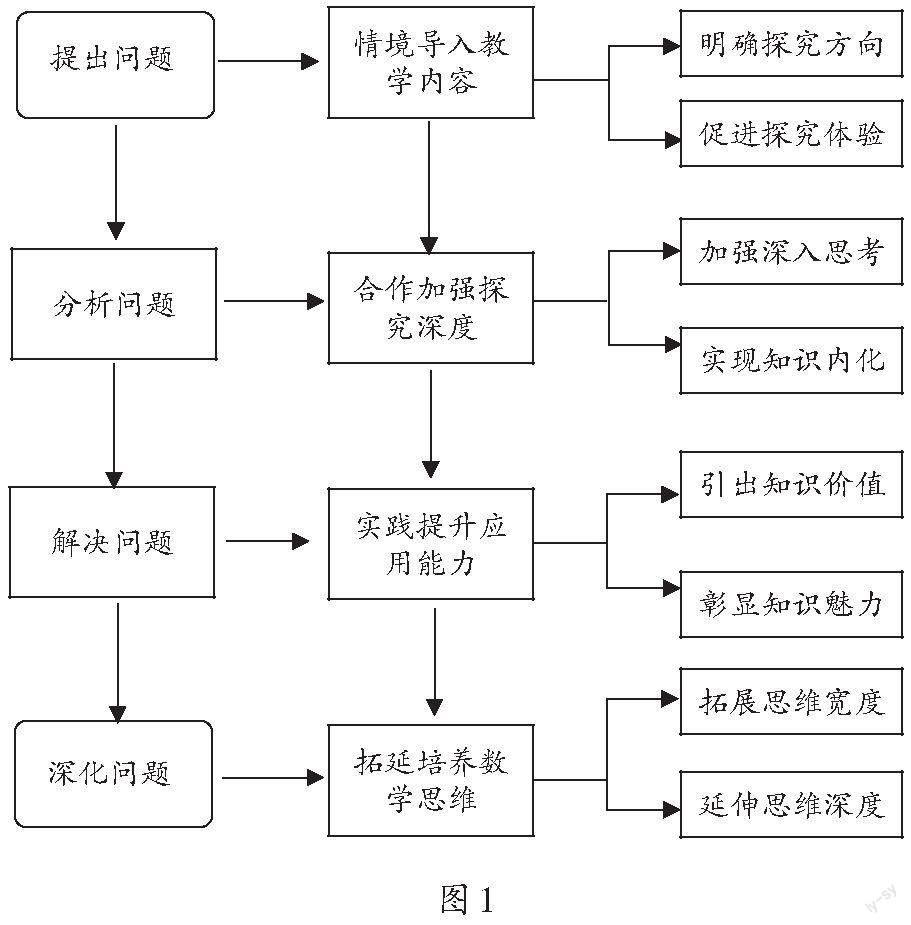
笔者通过“提出问题→分析问题→解决问题→深化问题”四个环节来开展深度教学，由浅入深、层层递进，并对每个环节的教学过程进行了详细、具体化的操作展示（如图1），以逐步夯实学生的数学基础，锻炼学生的数学思维，提高学生的应用能力，培养学生良好的数学学习习惯。

二、以问题开展深度教学的实践论证

（一）创设情境，导入教学内容

1.以问题明确探究方向

问题①：请利用身边的物品绘制一个圆。

问题②：你能使用圆规绘制不同尺寸的圆吗？

由于不同学生的认知水平不同，教师需要借助对话互动、游戏等多种方式，引导学生思考并探索情境中的数学问题，促使他们提高从数学角度观察现实世界的能力。

例如，在出示问题①后，有的学生利用杯子的底部来画圆，有的学生使用胶带圈来画圆，不过大多数学生是利用圆规来画圆。基于这样的教学情况，笔者提出问题②，引导学生将注意力集中在“利用圆规画圆”上。整个绘制圆的过程直观展示了圆的本质特征，而选择不同工具绘制圆的过程则加深了学生对圆本质特征的思考。

2.以问题促进探究体验

问题③：为什么用圆规可以画出规范的圆？

问题④：为什么有的人用圆规画的圆不标准？

利用圆规画圆时，大部分学生都可以画出规范的圆，甚至有的学生可以独立描述绘制圆的各个步骤，但还有小部分学生未能真正理解用圆规画圆画得标准的原因。笔者抓住这一关键机会对学生提出问题④，引导学生探寻画圆的关键。

生1：这个圆里有许多小孔，可见他在画圆时圆规针尖移动了。

生2：这个圆的边缘不平整，可能是因为画圆的过程中圆规两脚之间的距离改变了。

生3：用圆规画圆时，最好持握圆规最上面的部分。若我们持握的是它的脚，那么画出的圆就不够规范。

师：你们说的基本正确，那我们应如何保证每次都能画出规范的圆呢？

生4：确保圆规针尖位置固定不变，且圆规两脚之间的距离也应保持不变。

由于语言能力所限，学生的表达可能不够标准，但他们想要表达的意思非常明确，且给出的建议都基于他們的实践体验。在画圆的活动中，学生的探索欲得到激发，且都能够热衷于分享自己的观点，这种由学生自主思考并得出结论的方式的教学效果往往比教师直接给出答案好得多。

（二）分组合作，延长探究深度

1.以问题促进深度思考

问题⑤：为什么有的人将圆画在纸的左边，有的人画在纸的右边？

问题⑥：为什么有的人画出的圆很大，有的人画出的却很小？

通过展示学生的画圆成果，可以发现学生画出的圆各式各样、不尽相同。利用问题⑤可以自然地引出圆的位置这一重要知识点，促使学生发现“圆心”对圆的位置的重要性；利用问题⑥可以很好地引出“半径”的概念，让学生明白“半径”与圆的大小之间的关系。在这一过程中，笔者借助问题引导学生从表面现象中提炼本质，进而提升其思维深度。若一开始笔者便询问：“什么是圆心？什么是半径？”这样直接的问题虽接近要点，却不足以激发学生对知识的深入探索欲。

在疑问的引导下，学生更加愿意主动探求答案，从而培养自身良好的学习思维。因此，教师在探究性教学中应重视提出与学生直接相关的问题，引导学生对自身的实际操作步骤进行思考，使其在思考中加深认知、积累经验。

2.以问题促进知识内化

实践、探究和交流是掌握数学知识以及锻炼数学思维的关键。因此，教师在教学过程中应当注重发挥学生的主观能动性，给予学生充分的课堂时间、空间，让学生有机会在实验中观测、推断、体会和反思。为了让学生深入研究圆的基本特征，笔者事先为学生准备了不同半径的圆形纸片，采用开放式教学方式，鼓励学生在课堂上自由发挥，为创意思考提供平台。

问题⑦：通过这个实验你发现了什么？

生1：我先在一张纸片上画出几条半径，然后用直尺测量其长度，发现每条半径的长度都相同。

生2：我剪下与半径同样长的一根绳子，将绳子的一端固定在圆心，另一端绕边缘旋转一圈，发现绳子的另一端始终在圆的边缘上。

问题⑧：谁还有其他发现？

生3：我发现不论从圆心画出多少条线，只要它们都到达圆的边缘，它们的长度就都是一样的。

师：你的想法非常特别！你能说说为什么所有从圆心到边缘的线的长度都是一样的吗？

生4：因为圆心与边缘上任意一点的连线都可以视为半径，而半径的特征就是同一个圆的所有半径相等。

生5：我发现同一个圆内两条半径的长度之和等于一条直径的长度。

在教学“圆的认识”时，若一味采取折叠、测量、对比等活动引出“圆有无数条半径”“同一个圆的所有直径长度相等”等知识点，并采取不断训练的方式让学生加深理解，难免会忽略对学生逻辑推理能力的培养，致使部分学生因未真正理解“圆”而强行记忆。因此，教师应鼓励学生进行推测、实证，再进行总结和应用，促使其主动思考并开展逻辑推理，从而深入理解圆的本质特征。

（三）结合实践，提升应用能力

1.以问题引出知识价值

问题⑨：你能从数学的角度解释车轮为什么要做成圆的，车轴为什么装在车轮的中心吗？

生1：圆形的轮子没有边角，可以在地面上流畅运动。

生2：假如轮子是方形的，它转动时会产生颠簸，很不平稳。

生3：车轴位于圆形车轮的中心，行驶时就很稳定，如果车轴偏离中心，行驶时就会不稳定。

师：为什么车轴位于圆心时，车能够平稳地行驶？

生4：因为圆的半径长度是固定的，车轴在圆心时，它到地面的距离始终是相同的，这就能让车辆行驶平稳。

笔者按照“生活中的圆→数学中的圆→圆的特征→回归生活”的顺序教学，通过“发现问题→操作探究→知识内化→应用”的流程紧密结合学生的生活实践提出问题，发展学生的高阶思维。经过教与学的互动，学生不仅能从实际问题中抽象出圆的关键特征，还展示了他们对这一特征的个性化认识。

2.以问题彰显数学魅力

圆是生活中常见的形状，为了让学生更深刻地感受圆的价值，教师可以展示一系列与圆有关的图片：圆形的时钟，时针、分针、秒针围绕中心旋转的轨迹是圆形；古老的建筑，如罗马斗兽场的设计使用了圆形和半圆形；舞蹈和绘画运用了圆形这一元素；石子投入湖中荡开一圈又一圈的圆形波纹；太阳下盛开的向日葵；阳光产生的圆形光晕。还可以向学生渗透：在中国文化中，圆象征着团聚和完整，在表达美好祝愿时，人们也喜欢使用“圆满”和“圆梦”等词汇，以及许多文学作品往往是圆满的大结局。在数学课堂教学中引导学生深入探索圆的历史、文化和美感，能让他们更加珍视和欣赏圆的无尽魅力。

（四）拓展延伸，强化数学思维

1.以问题拓展思维宽度

“圆的认识”是被安排在学生对圆有了直观认识以及对平面图形有了较为系统认知后学习的。笔者通过如下同一份问卷来了解学生学习这一课前后的情况，以及学生对知识的内化程度，并根据学情调整教学内容，从而拓展学生的思维宽度。

（1）你对圆了解吗？

A.很了解        B.一般        C.不了解

（2）你能画出一个规范的圆吗？

A.可以        B.可以，但不一定规范

C.不可以

（3）你认为圆形物体在生活中的价值如何？

A.价值很大        B.价值一般        C.没有价值

（4）关于圆，你最想了解哪些问题？

分析课前调查数据，笔者发现多数学生对圆的知识掌握较浅，且不同学生在理解程度上表现出较大差距，关于问卷最后的开放性问题，学生主要提出以下问题：

①如何快速画出一个圆？

②如何画出任意大小的圆？

③如何快速计算圆的周长与面积？其计算公式是什么？

④学习圆对我们的生活有什么帮助？

在学生学习“圆的认识”一课后，笔者发现学生提出的问题变得更加深刻且具体，提出的问题有：

①祖冲之使用了哪些方法来计算圆周率？

②通过计算机可以将圆周率计算到小数点后多少位？

③为什么生活中常见的下水道井盖是圆形的，还有部分是方形的？

④圆形有那么多好处，为什么不将房子建成圆形？

⑤现实生活中有没有完美而规范的圆形物体？

⑥画圆的最好方式就是用圆规吗？

⑦圆是什么时候被发现并被定义的呢？

用同一份问卷对学生进行学习前后的两次调查，发现学生的想象力是非常丰富的，如果教师仅仅依照教学大纲开展教学活动，有可能会扼杀学生对知识的好奇心和探索欲。即使学生提出的某些问题超出了教材范围，教师也应适当进行课堂拓展，以此激发学生的探究欲。

2.以问题延伸思维深度

不断地质疑问难、主动地深入探索、及时地自我反思……这些都是学生养成良好学习习惯的有效方式。因此，在对上述的问卷反馈信息进行分析、总结之后，笔者从中挑选出多数学生感兴趣的问题，构建班级共同目标，引导学生开展更为深入的研究。探究内容及步骤如下。

【探究问题】为什么生活中常见的下水道井盖是圆形的？

【探究形式】分组合作、自主探究。

【探究方法】上网查阅资料、到图书馆查阅资料、组内成员商议或向小区物业人员寻求帮助。

【探究结果】

大多数井盖是圆形的原因如下。

①安全性高。无论如何旋转，圆形井盖的直径始终大于其下方的开口，圆形井盖不会突然掉进井内。而其他形状，如正方形或矩形，如果斜着放置，可能会掉入井内。

②易于移动、安装。由于其圆形结构，工作人员可以通过滚动轻松移动它，而不必费力地抬起它，且在重新放置圆形井盖时不需要对其进行位置对齐。

③均匀分布压力。圆形可以更均匀地分散地面上的压力，有效降低因为重型车辆经过而导致的损坏风险。

小区下水道井井盖为方形的原因如下。

由于某些下水道井的深度较浅，其内部空间要求也不大，为了最大程度上便于施工，自然就将其做成了方形。除此之外，住宅小区内部的地砖多为方形，如果配备圆形的井盖，则会给铺砖工作带来极大的不便。因此，从人工成本的角度考虑，方形更为适宜。生活中除圆形和方形外，还有很多其他形状的井盖，这是根据不同场景需要设计的。

在上述探究过程中，学生不仅得到了认知方面的提升，还获得了反思、概括、举一反三等方面的能力。另外，学生还能深刻感受到数学知识在生活中的应用价值，领悟到“数学源于生活，又应用于生活”的深刻道理。

综上所述，数学学习实际上就是不断提出、分析、解决以及深化问题的过程。对于实行数学深度教学，教师应该认识到学生的既有知识和能力，并在遵循目的性、顺序性以及适度性三原则的基础上优化教学框架，通过合适的问题场景引导学生发现自己经验的局限，并激励他们开展探究性学习活动，不断深入探索数学的奥秘，开启数学深度学习之旅。

［ 参 考 文 献 ］

[1] 付丽云.深度教学视域下谈小学数学高效课堂的构建[J].学周刊，2023（28）：52-54.

[2] 柳苗.小学数学“问题解决”深度教学研究[D].荆州：长江大学，2023.

[3] 孙颖.小学数学深度教学应“深”在何处？[J].江苏教育研究，2023（7）：74-78.

[4] 姜丽华.深度挖掘 探求本质：论小学数学深度教学的有效策略[J].数学学习与研究，2023（7）：50-52.

[5] 刘娟.小学数学深度教学建设探析[J].新課程教学（电子版），2022（20）：75-76.