基于谱聚类的自加权多视图聚类算法研究

徐浩琦，侯建，袁华强

（东莞理工学院计算机科学与技术学院，广东东莞 523000）

现实中样本的特征多是来自不同的视图。多视图聚类就是利用不同视图的特征进行聚类[1]。多视图数据融合策略一般可以分为三种，分别是一致性策略、互补性策略和兼容性策略。一致性策略算法一般会最大化不同视图之间的相关性，然后从中提取出视图间的共享成分进行分析[2]。互补策略主要是显示保留多视图数据中视图间的共享成分和每个单视图的特有信息成分[3]。而兼容性策略主要是自适应地兼容共享信息和特有信息[4]。

文献[5]提出将跨视图图扩散用于多视图聚类统一图的学习，但是该算法没有考虑不同视图之间重要性的差异。文献[6]提出了一种基于子空间融合的多视图聚类算法，但是该算法需要对不同视图的权重进行单独优化。该文提出了一种基于谱聚类的自加权多视图聚类算法。该算法可以自动为视图添加权重，同时利用秩约束来控制全局图的连通分量，使连通分量个数与簇的个数相同，以直接从图结构中获得聚类结果。

1 相关工作

谱聚类是一种被广泛使用的聚类算法。其中谱聚类的归一化割（NCUT）算法更是在诸多领域取得了较好的效果。但是，谱聚类算法的效果高度依赖于相似度矩阵的质量。如果可以直接构建出具有k个连通分量的相似度图，那么就可以直接从图的本身获得聚类结果，通过这一方式来为每个单一视图进行聚类。对于数据集X={X(1),X(2),…,X(nv)}，其中X(i)代表第i个视图的原始数据。根据文献[7]，将归一化拉普拉斯矩阵L的前k个最小特征值对应的特征向量组成的矩阵H视为原始数据X的低维嵌入，可以通过以下目标函数得出图的相似度距阵W：

其中，W受约束条件W1=1 的约束。这一约束可以将得到的拉普拉斯矩阵控制为归一化拉普拉斯矩阵，即L=I-W。随着该目标函数不断优化，最终使得L的前k个最小特征值的和为0。通过该目标函数得出的W具有理想的邻居分配，并且其连通分量个数与簇的个数相同。

这里引入一个定理，以进行接下来的论述：

定理1：图G的拉普拉斯矩阵L的0 特征值的重数等于图G连通分量个数[8]。

由定理1 可以得出，可以通过控制图的拉普拉斯矩阵的0 特征值重数，来控制图的连通分量个数。不失一般性，将L的特征按照从小到大排列，由于拉普拉斯矩阵的最小特征值为0，如果前k个最小特征值之和为0，则有L的秩rank(L)=n-k，根据定理1 进一步可得，图的连通分量个数为k。由此可以得到约束条件：=0 。该约束条件可以控制图的连通分量个数始终为k，保证了最终的聚类结果可以从图的结构中直接得出。

目标函数（1）的优化结果可以通过优化两个子问题交替求解，直到L的前k个最小特征值之和为0。第一个子问题是求解方程特征值分解问题。第二个子问题则是单纯形空间上的欧几里得投影问题[9]。

2 多视图聚类算法

2.1 自动加权算法

当面对多视图数据时，不同的视图可能具有不同的重要性。因此，需要给不同的视图增加权重。一些算法选择使用拉格朗日乘数法，通过最大梯度对权重进行优化，但是这种方法需要给权重添加一个超参数。过多的参数将会给算法带来很大的不确定性，调整参数的过程也将会产生很大的计算开支。鉴于上述原因，选择使用自加权[10-11]的方式对每个视图进行加权。构造了如下形式的目标函数：

其中，W(v)=假设H(v)可以由式（2）进行计算，那么H(v)就可以用来更新之前的W(v)。可以使用循环迭代的方式对上式进行优化。

2.2 全局图的构造

多视图聚类需要将不同视图中的信息汇集到一起，学习得到一个全局图。为了使得到的全局图能充分包含各个单视图的信息，需要在学习过程中将全局图与各个单视图之间的差距控制到最小。为此，需要构造出一个更能体现每个单视图特征的矩阵。

首先，对每个单视图的特征矩阵进行处理，使其可以更好地表达每个视图的结构信息。为此，使用谱聚类的归一化割算法，得到每个视图的低维嵌入矩阵H。这样的处理能够使图中的各个样本点分配到最佳邻居的结构。再利用自加权的方式，为每个视图添加各自的权重。这样就可以协同所有视图共同取得最小的归一化割，以此来学习到合适的嵌入矩阵。

为了使嵌入矩阵可以更好地体现原视图的图结构，采用线性核函数k(xi,xj)=来计算每个视图在经过NCUT 之后的相似度矩阵HHT。理想状态下，HHT为对角矩阵。可以利用这些不同的视图得到一个全局图矩阵S。该全局图可以通过最小化S与不同视图的对角矩阵H(v)(H(v))T之间的差值mv得到：

选择线性核来度量相似性的主要原因[12]在于，拉普拉斯谱聚类中使用的相似性度量已经考虑了数据中存在的非线性结构，并且嵌入矩阵H(·)是实值的聚类指标矩阵，因此可以认为该结构服从线性相似性。

该算法有以下要点。首先，算法初始化过程中，每个视图的相似度图可以通过式（1）得到。其次，利用W得到每个视图的嵌入矩阵H。同时，可以利用rank(LS)=n-k的约束，使最终学习到的全局图S恰好有k个连通分量，每个连通分量恰好可以作为一个簇。最后，通过最小化全局图与每个视图的H(v)(H(v))T矩阵之间的距离，可以得到更优的全局图S。目标函数如下：

其中，LS是S的归一化拉普拉斯矩阵。整体算法思路如图1 所示。

图1 算法思路

2.3 算法优化

目标问题可以分为两个子问题，分别固定其中一个目标变量，更新另一个目标变量，交替循环迭代求解。

2.3.1 更新H(v)

第一个子问题中，将变量S固定视为常数，更新变量H(v)。此时，目标函数变为：

同时考虑约束条件(H(v))TH(v)=I，原问题可以等价为：

该方程的解即为[W(v)(W(v)-I)+2S]的前k个最大的特征值对应的特征向量组成的矩阵。

2.3.2 更新S

第二个子问题中，将变量H(v)固定视为常数，更新变量S，此时，目标函数变为：

约束条件rank(LS)=n-k可以用minTr(HTLSH)来实现。令Q=则式（7）可以等价为：

其中，γ是权衡参数。

式（8）中的变量在不同的列之间是相互独立的，则上述问题可以表示为：

其中，sj表示S的第j列。为了方便表示，令上述问题可以等价为一个在单纯形空间上的拉格朗日投影问题。根据Karush-Kuhn-Tucker(KKT)条件[13]，可以验证最优解为：

在式（1）和式（8）中出现的权衡参数α和γ是用来实现约束条件rank(L)=n-k的。它们将会在算法优化过程中自动求解。它们的初始值将会设置为1，并且在迭代期间会根据不断优化，直到

2.4 算法步骤

算法整体流程如下所示：

输入：原始数据X={X(1),X(2),…,}，视图数nv，簇个数k；

输出：恰有k个连通分量的全局图S；

初始化：初始的相似度矩阵W和嵌入矩阵H0由式（1）计算得到，初始全局图矩阵S0由得到。此处的H0由拉普拉斯矩阵LS的前k个最小特征值对应的特征向量组成。

步骤1：对于数据的每一个视图v∈{1,2,…,nv}，通过式（6）求得当前具有最佳邻居分配的H(v)；

步骤2：对每一个样本j∈{1,2,…,n}，通过式（10）更新sj；

步骤3：利用LS的前k个最小的特征值对应的特征向量组成H；

步骤4：重复步骤2-3，直到S恰有k个连通分量；

步骤5：重复步骤1-4，直到算法收敛。

算法流程如图2 所示。

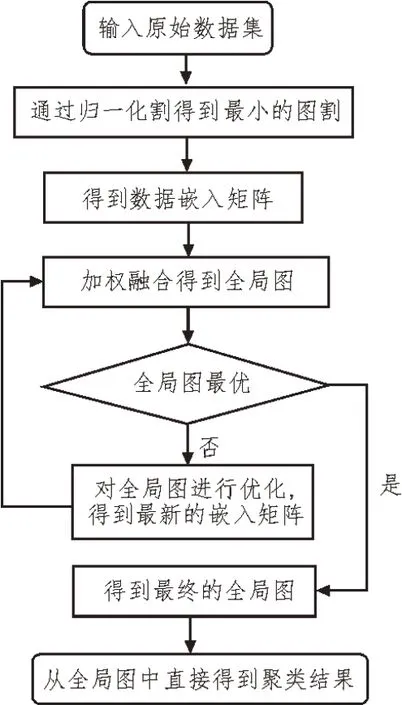
图2 算法流程图

3 实验

将该文算法在一些数据集上进行了实验测试，以验证算法的有效性。首先引入了两个在多视图聚类算法实验中广泛使用的数据集。然后将该算法与另外几种常用于比较的多视图聚类算法进行对比，并对实验结果进行讨论。

3.1 数据集

COIL-20 数据集由20 个类别的1 440 幅图像组成，每个类别有72 幅图像。每个样本由4 个不同的特征表示，这些特征组成了4 个视图。

Mfeat数据集来自UCI机器学习资源库。该数据集由2 000 个样本(从0 到9 的每个类种各包含200 个样本)组成。其使用了6 个不同的特征组成了相应的视图，包括76 个字符形状傅里叶系数、216 个轮廓系数、64 个Karhuen-Love 系数、240 个2×3 窗口的像素平均值、47 个Zernike 矩和6 个形态特征。

3.2 实验结果与比较

将提出的算法与另外3 种多视图聚类算法进行了比较。这些算法分别是谱聚类的亲和度聚合算法[14]（AASC）、稳健的多视图谱聚类算法[15]（RMSC），以及多视图共识图聚类算法[16]（MCGC）。表1 和表2中展示了该文算法与3 个对比算法在两个数据集上进行10 次实验的平均结果。

表1 算法在COIL20数据集上的运行结果

表2 算法在Mfeat数据集上的运行结果

从表1 和表2 中可以看出，该文算法在COIL20、Mfeat 数据集上的性能更优，其归一化互信息NMI(Normalized Mutual Information)、精确度ACC(Accuracy)和纯度PU(Purity)值均高于另外3 种算法。RMSC 算法在Mfeat 数据集上的效果要远差于其他对比算法，其原因可能在于该算法的参数选择方法限制了其在不同数据集上的通用性。

4 结论

该文提出了一种基于谱聚类的自动加权多视图聚类算法。该算法通过对相似度矩阵使用秩约束，来使矩阵的连通分量个数与簇个数相同，从而可以直接通过图的结构得到聚类结果。通过最小化全局图与各单视图优化后的相似度矩阵之间的距离得到最终的相似度图。该算法还考虑到了每个视图的重要性的差异，通过添加自动加权的方式，减少了模型的参数个数，使得模型具有更好的鲁棒性。该算法在两个真实数据集上运行，并与其他3 个多视图算法进行对比，在多个评价指标上取得了更优的结果，可以认为该算法具有更优的性能。

在未来的工作中，将会考虑使用其他的距离度量方式，来提高算法应对噪声的能力，即提高算法的鲁棒性。