基于自适应模拟退火优化算法的集合式电容器局放定位研究

李欢，国江，陶维亮，杨欣婷，罗可心

（1.武汉大学电子信息学院，湖北武汉 430072；2.中国电力科学研究院，湖北武汉 430074）

集合式电容器因其占地面积小、安装简便、抗震性能好、使用寿命长等特点，在用地紧张、抗震要求高、高海拔等恶劣环境中具有显著的应用优势[1]。然而，电容器内部的局部放电问题，是电容器故障的主要原因之一[2-3]。目前，局部放电定位技术主要包括电气定位法、特高频定位法和超声波定位法等。电气定位法[4-6]、特高频定位法[7-9]易受电磁干扰。而超声波定位法具有抗电磁干扰、非侵入式、在线带电检测等优势，更适用于集合式电容器这种复杂电磁环境工作的全封闭电力设备的局放在线检测。

为此，提出了一种自适应模拟退火粒子群超声定位方法。该方法结合超声检测法，并通过对参数自适应优化及结合模拟退火和轮盘赌，提高定位的准确性和稳定性。

1 局部放电超声定位数学模型

根据集合式电容器的物理模型，假设局部放电源坐标为P(x,y,z)，外部放置有n个超声波传感器，坐标Si(xi,yi,zi),i=1,2,…,n。集合式电容器局部放电定位模型如图1 所示。

图1 集合式电容器局部放电定位模型

以第一个传感器为参考传感器，根据传感器接受信号后的反馈处理可以计算出其他路和参考传感器的时延差Δti1。在超声波传播速度v未知的情况下，那么距离差可以表达为声速与时延差的乘积，如式（1）所示：

根据几何关系，得到局放源P到第i个传感器与第一个传感器的距离差，如式（2）所示：

因此，每组传感器的误差值可表示为关于x,y,z,v的函数，如式（3）所示：

一般来说，式（3）是超定方程，精确解很难得到，只能求得最优解。为了定位局放源，可以概括为约束优化问题，如式（4）所示：

2 集合式电容器局放故障自适应模拟退火优化定位算法

在得到基于时间差的集合式电容器定位的适应度函数后，便将问题转化求解极值问题。提出一种自适应模拟退火优化算法（SA-FAPSO）。算法在粒子群路径搜索基础上，增加模拟退火和轮盘赌结合的变异策略，增加后期突破局部最优解的能力。整体流程图如图2 所示。

图2 自适应模拟退火优化定位算法流程图

2.1 粒子群算法（PSO）

粒子群算法模拟了鸟类觅食行为，通过群体中个体之间的信息交流和协作来找到问题的最优解。那么对于局放源定位，就可以将每一个粒子看成符合局放源条件可能的解，粒子位置对应解的坐标和声速，以在某个范围的速度在4 维空间的某个范围内进行寻找，并通过目标函数的适应度值判断当前条件的好坏程度，更新个体极值pgest和全局极值gbest。通过跟踪个体极值和全局极值不断调整自己的速度和位置。第i个粒子在第d次迭代中，速度更新公式如式（5）所示：

位置更新公式如式（6）所示：

2.2 自适应粒子群算法(FAPSO)

自适应粒子群算法（FAPSO）通过改进粒子群算法中的惯性权重和学习因子，提高搜索能力，增加收敛速度。

2.2.1 自适应惯性权重

粒子群搜索过程中，粒子速度上一代对这一代的惯性权重影响w。当w较大时全局搜索能力更强；反之，局部搜索能力更强。为了更好地平衡算法的全局和局部搜索能力，使用了根据个体和群体适应度不同而自适应改变惯性权重的方法[10]，如式（7）所示：

式中，wmax、wmin分别为最大、最小惯性权重；代表第i个粒子第d次迭代的惯性权重；为第i个粒子第d代的适应度；表示第d次迭代种群的平均适应度；表示第d次迭代种群的最小适应度。

2.2.2 压缩因子

粒子群算法中，较大的个体学习因子c1，会让粒子过多地在局部范围内搜索；而较大的社会学习因子c2，则会使粒子过早收敛于局部极值。为了有效地控制粒子的收敛速度，平衡搜索能力，文献[11]使用了收缩因子改善粒子群算法。如式（8）所示：

修改后的速度更新公式如式（9）所示：

2.3 自适应模拟退火优化算法(SA-FAPSO)

为增强算法后期的搜索能力，提出了结合模拟退火和轮盘赌的变异策略算法，自适应模拟退火优化算法（SA-FAPSO）。该算法在粒子群路径搜索方式上增加一种变异策略，增加后期突破局部最优解的能力。将两种算法结合起来，可以在全局搜索的同时，进行精细化选择，从而更好地遍历整个搜索空间，提高搜索效率和优化效果。

2.3.1 模拟退火

根据模拟退火思想[12-13]，粒子群不断产生新的模拟局放源条件，以一定的概率接受新的条件，最终使模拟局放源的粒子达到最优解。该变异概率随着粒子与全局极值的差距减小而增大。为保留粒子群算法路径更新的优势，就要使变异影响前期小后期大，因此设置变异影响因子“S”随着迭代次数增加而增大。变异概率公式如式(10)所示：

式中，f(xi)、f(gbest)分别为在第i个模拟局放源的粒子和全局最优粒子的适应度；初期”S”取ln5/f(gbest)，每次迭代除以退火常数lamda，使影响因子S增大。

2.3.2 轮盘赌选择

上述模拟退火给每个模拟局放源的粒子都赋予取代全局极值的概率。但实际上，每次迭代全局极值最后只可能会被一个模拟局放源的粒子取代。为增加变异效率，采用轮盘赌策略[14-15]，将每个模拟局放源的粒子视为轮盘上的一部分，所占的扇区大小与其取代概率成正比。通过轮盘选择的方式将变异概率重新整合、分配概率。

第i个模拟粒子被选择的概率如式（11）所示：

累积概率如式（12）所示：

自适应模拟退火粒子群优化算法的主要步骤如下：

Step1：设置参数，随机初始化模拟局放源的粒子群；

Step2：计算适应度，将当前个体最优和全局最优解分别存储到pbest和gbest中：

Step3：初始化影响因子S；

Step4：计算惯性权重，并更新粒子的速度和位置（模拟局放源的条件）；

Step5：更新粒子个体极值和全局极值；

Step6：根据模拟退火和轮盘赌，判断接受哪个粒子作为新的全局极值。

Step7：进行退火操作，S=S/lamda；

Step8：判断算法是否到达最大迭代次数或容忍度小于阈值的次数达到最大计数值，如果是则退出迭代，否则转向Step4；

Step9：输出全局最优解，运行结束。

3 实验结果与分析

设计仿真实验定量分析和验证算法的特性和性能。实验中集合器电容器尺寸为2 000 mm×2 000 mm×2 000 mm，放置5 个传感器贴于电容器外部同一侧，坐标分别为S1(0,500,500),S2(0,500,1 500),S3(0,1 000,1 000),S4(0,1 500,500),S5(0,1 500,1 500)。

实验参数选择如下：

粒子数n=30，最大迭代次数10 000，个体学习因子c1=2.05，社会学习因子c2=2.05。

自适应粒子群算法(FAPSO)：最大惯性权重wmax=0.9，最小惯性权重wmin=0.4；

自适应模拟退火算法(SA-FAPSO)：退火常数lamb=0.9。

引入高斯随机变异粒子群算法[16]进行对比：最大、最小变异概率pmax=0.3,pmin=0.1；

自适应变异算法(AMPSO)是结合了粒子群参数自适应优化方法的变异粒子群算法。

退出迭代功能：容忍度为10-20，最大计数值max_count=30。

3.1 误差分析

为对比分析算法性能，观察粒子群算法（PSO）、自适应粒子群算法（FAPSO）、变异算法、自适应变异粒子群算法（AMPSO）、模拟退火算法(SAPSO)、自适应模拟退火粒子群算法（SA-FAPSO）六种算法500次独立重复实验的平均误差、最大误差、平均迭代次数，如表1 所示。

表1 六种算法的性能比较

从上表可以看出，粒子群参数自适应优化的方法可以明显提高算法精度，但会一定程度上增加迭代次数。再通过增加变异，SA-FAPSO 和AMPSO 拥有更好的精度，平均误差远小于PSO、变异粒子群、FAPSO、SAPSO，最大误差也有所改善。

3.2 收敛过程分析

为分析算法收敛过程，进行了相同条件下对比分析，FAPSO、AMPSO、SA-FAPSO 的适应度值随迭代次数变化关系图，如图3 所示。

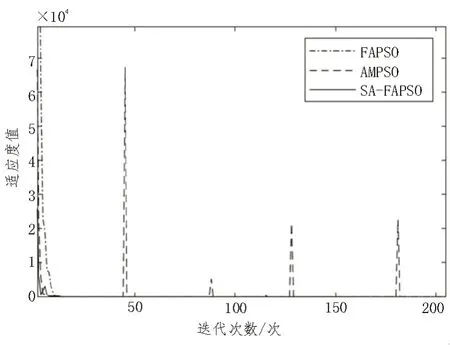
图3 三种算法的收敛曲线对比

横轴代表迭代次数，纵轴代表适应度值。从上图可以看出，到迭代后期，SA-FAPSO 突破局部最优解的能力依然很强。此外，由于AMPSO 随机变异的特性，变异后的粒子可能会出现适应度值较大的情况，即上图中AMPSO 出现的异常点。对比变异方式，SA-FAPSO 的变异只会被当代粒子群中粒子取代，影响更小而且可控。同时，SA-FAPSO 相比AMPSO 的适应度值波动小的特点，会使其更容易退出迭代功能。综上，SA-FAPSO 增加的变异能力不仅增强其后期的搜索能力，同时适应于退出迭代功能，便于判断是否达到最优解。

3.3 迭代次数波动分析

观察到FAPSO、AMPSO 和SA-FAPSO 收敛特性存在差异，分析迭代次数波动范围也应存在差异。为此，设计三组500 次重复实验，观察迭代次数波动情况，如图4 所示。

图4 三种算法的迭代次数曲线图

横轴表示500 次实验的实验编号，纵轴表示迭代次数。从图中看到，SA-FAPSO 的波动远小于AMPSO，也小于FAPSO。这是因为SA-FAPSO 对于FAPSO 后期有更强的搜索能力，同时相比AMPSO 在路径搜索更新的粒子群中选择更新，变异范围更小、更可控，适应度波动更小，更容易判断是否达到最优解，迭代次数波动更小。这也体现在表1 中平均迭代次数：SA-FAPSO＜FAPSO＜AMPSO。

4 结论

针对集合式电容器内部局部放电源定位检测问题，提出了一种自适应模拟退火粒子群超声定位算法。应用于集合式电容器的局部放电定位上，建立了合理的数学模型和求解算法，并通过仿真分析验证，得出了SA-FAPSO 具有更好的定位精度、更强收敛能力、更快的收敛速度，以及更稳定的优点。为解决集合式电容器局部放电定位问题提供了有效的解决方案。