河谷型城市中低运量轨道交通制式选择研究

庞登瑀，杨懿轩

(四川省交通运输发展战略和规划科学研究院,成都 610041)

引言

轨道交通在公共交通系统中占据重要的地位,深圳、成都等以地铁等大运量轨道交通为主的特大城市轨道交通分担率已超60%,而根据《国务院办公厅关于进一步加强城市轨道交通规划建设管理的意见(国办发[2018]52号)》等文件,大中城市在人口、经济、客流等方面较难达到申报建设地铁、轻轨等大运量轨道交通的条件[1-2],以单轨、有轨电车等为代表的中低运量轨道交通将成为大中城市的最佳选择。我国目前有50%左右的人口居住在山地城市,其中河谷型城市是其占有量最大的类型之一,且大部分属于大中城市,如西宁、宝鸡、西昌等[3-4],但相比于平原地区,河谷型城市在构建轨道交通时会因较强的地理、环境特征等受到更多条件限制。

选择合理的制式是构建轨道交通的第一步,如何能高效、科学地挑选出某城市适用的轨道交通制式这一问题逐渐受到了国内外学者的关注,主要围绕不同制式技术特征、制式选择方法、制式选择因素等方面开展了相关研究[5-7],但针对河谷型城市的轨道交通研究,特别是中低运量轨道交通制式选择的研究较少。因此,本文以中低运量轨道交通系统为基础、河谷型城市为研究对象,分析其在制式选择时的主要考虑因素,以此建立评价指标体系,构建基于熵权-层次分析法的组合权重模型,并进行实例分析,填补研究空白,为河谷型城市提供快速、科学的中低运量轨道交通制式选择决策思路。

1 中低运量轨道交通系统概况

1.1 分类及特征

中低运量城市轨道交通是指平均运输能力在0.5万～3万人次/h之间、旅行速度高于常规公交的交通系统[8]。目前已逐步形成由跨座式单轨、悬挂式单轨、自动旅客捷运系统、中低速磁浮列车、现代有轨电车、智能轨道快运列车等多种制式组成的轨道交通系统,上述制式类别的主要技术、常用场景、比较优势、系统缺点见表1。

表1 中低运量轨道交通分类及主要特征[5,9-11]Tab.1 Classification and main characteristics of medium and low capacity rail transit

1.2 建设情况

目前国内已有近30个城市开通运营中低运量轨道交通,合计运营里程约750 km,约占轨道交通系统运营里程的6%。

由表2可知,中低运量轨道交通制式中,现代有轨电车应用规模最大,已有超18个城市运营该制式系统,里程约500 km;跨座式单轨目前主要应用于重庆、银川等地,运营里程约150 km;中低速磁浮列车主要应用于北京和长沙,运营里程约30 km;自动旅客捷运系统主要在北京、广州等机场设置,运营里程约17 km;智轨系统面世推广时间最晚,但增长速度较快,已在宜宾、株洲等城市得到推广,运营里程已超过50 km。

2 河谷型城市对中低运量轨道交通制式的主要考虑因素

2.1 河谷型城市概述

我国山地占据了陆地面积的2/3,全国有超300个城市位于山区,而河谷城市是山地城市占据数量最多的一类,他们不仅是城镇化建设的重要根据地,更是山区经济的发展核心。河谷型城市是指城市建成区在河谷中形成和发展的城市,一般处于河流的中上游地区,发展空间常受到地形、河流的直接限制[12],城市空间拓展的方向一般沿河流带状发展或沿垂直河流的山体上拓展[4]。

我国河谷型城市主要分布在西部地区,包括兰州、西宁、重庆、天水、宝鸡、西昌、攀枝花、延安、永登等城市,居民人口数量从30万～2 000万人不等,但主要集中于100万～500万人的大中城市之间。

2.2 考虑因素分析

轨道交通是开拓城市发展空间的重要手段,需因地制宜综合考虑各类因素。与平原地区相比,河谷型城市在经济发展、地质条件、生态环境等方面的约束更多,对轨道交通制式选择提出了更高的要求,具体分析如下。

(1)要求更加契合社会经济发展水平。河谷型城市整体经济发展水平与前排发达城市还存在一定差距,政府基础设施建设投资资金有限,项目主体及配套招商引资也较为困难,应尽量选择综合造价合理、建设成本适当的制式系统,避免过度超前发展带来地方财政难以为继的困境。

(2)要求更加匹配客流发展特征。中低运量轨道交通系统制式较多,不同制式系统适用于不同的客流特征,特别是河谷型城市由于城市空间格局较为特殊,其轨道交通线路建设常沿河流或主干道敷设,与环形、放射型城市相比更容易在早晚高峰时段产生较大的客流量变化[13],同时,不同制式的适用场景也不同,因此在选择轨道交通制式时,应选择可承载线路客流量的峰值和变化、符合线路使用功能的轨道交通制式。

(3)要求更加适应地形地质条件。河谷型城市在城市主体发展时,通常会受到河流、山地、丘陵等地形的直接限制(如山体与丘陵的坡度、相对高度、植被条件、地质条件等),致使其地形呈现高低悬殊明显的特征[14],且道路的非直线系数通常较大[15],在选择中低运量轨道交通制式时,需充分考虑不同制式系统的转弯半径大小和爬坡能力水平,以更好适应复杂的地形地貌环境,支撑城市空间拓展开发。

(4)要求更加凸显绿色安全底色。目前我国正处于高质量发展的关键阶段,对绿色、安全建设等均提出了相关要求,河谷型城市的容量和规模有更加明显限制[16],大气污染物更不易排放,土地资源更为紧张,也更容易发生坍塌、滑坡、洪涝等次生灾害,在选择中低运量轨道交通制式时,需着重考虑运营时产生能耗[17]和噪声更低、土地占用面积较小、安全性能更高的制式系统,支撑引领经济社会高质量发展。

3 基于熵权-层次分析法的组合权重制式选择模型

中低运量轨道交通制式的选择本质上属于综合决策问题,解决这类问题的常用方法有层次分析法、数据包络分析等,本文将定性、定量结合,采用层次分析法和熵权法,通过引入主观偏好系数构建组合权重进行制式选择[18-19]。

3.1 基本方法介绍

3.1.1 层次分析法

层次分析法是多属性决策分析模型,计算步骤如下[20]。

Step1.构建由决策目标(目标层)、考虑因素(准则层)、决策对象(方案层)组成的层次结构模型。

Step2.分别对目标层—准则层、准则层—方案层的指标重要程度两两比较,利用“1～9标度法”赋予权重,构建判断矩阵

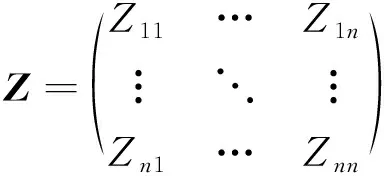
(1)

式中,n表示有n个因素。

Step4.当所有判断矩阵通过一致性检验以后,对各层次指标权重进行加权综合,最终得到方案层各指标相对于目标层的权重W。

3.1.2 熵权法

熵权法是通过判断指标信息熵的大小来赋予权重,若某个指标的熵值越小,说明该指标能提供更多的信息,在评价模型中就更重要,反之,若某个指标的熵值越大,在评价模型中就更不重要。该方法广泛应用于综合评价模型,计算方法如下。

Step1.设评价模型中有p个对象,q个评价指标,初始化决策矩阵Z=(Zij)p×p,(i=1,2,…,p;j=1,2,…,q),对数据归一化处理形成标准化矩阵Y,元素为Yij,则

(2)

Step2.计算指标yj(j=1,2,…,q)的信息熵

(3)

Step3.计算各指标相对于目标层的客观熵权

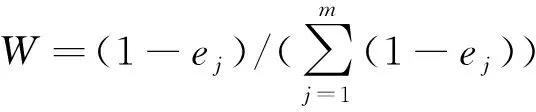
(4)

3.1.3 主观偏好系数

主观偏好系数主要用于解决需主观评价方案重要度的问题,常用于两种及以上模型的综合评价,设θ为主观偏好系数,i为需要评价的个数,则

当i=2,

w=θ×w1+(1-θ)×w2

(5)

当i=3,

w=θ1×w1+θ2×w2+(1-θ1-θ2)×w3

(6)

其中,θ取值越大代表对应模型权重越大,具体取值依据模型蕴含信息量、可靠性高低进行主观赋值。

3.2 基于熵权-层次分析法的组合权重模型计算步骤

模型计算主要有构建评价指标体系,基于层次分析法和熵权法计算方案权重,引入主观偏好系数计算组合权重等3个步骤,见图1。

图1 基于熵权—层次分析法的组合权重模型计算步骤Fig.1 Calculation steps of combination weight model based on entropy weight-analytic hierarchy process method

3.2.1 构建评价指标体系

经研究,共有29个指标被用于多制式轨道交通制式选择研究(表3),其中客运能力、综合造价等指标选择比例为100%,土地占用等指标被选择比例较小,本文以此作为基础指标筛选库。

表3 相关文献指标选择比例情况[5,9-10,21]Tab.3 Selection ratio of relevant literature indicators

结合指标应用通用性、河谷地区特征、数据获取难度和中低运量轨道交通技术特征,提出了由城市适应性、系统经济性、社会效益性3个层次、16项指标构成的评价指标体系A,具体构成如表4所示,同时设仅保留定量指标的评价指标体系为A′。

表4 评价指标体系构成及各制式情况Tab.4 Composition of evaluation index system and data of various rail transit system

3.2.2 计算各类方案权重

(1)将指标体系A、A′分别用于层次分析法,以此为基础构建层次结构模型,通过专家打分法赋权得到判断矩阵,一致性检验通过后,分别得到方案权重为WAj(j=1,2,…,m)、WADj(j=1,2,…,m)。

(2)将指标体系A′应用于熵权法,得到方案权重为WSj(j=1,2,…,m)。

3.2.3 计算组合方案权重

引入主观偏好系数,对3类方案权重进行赋权,计算方案综合权重。设第一类方案权重为θ1,第二类方案权重为θ2,第三类方案权重为1-θ1-θ2,则方案组合权重

W=θ1×WAj+θ2×WADj+(1-θ1-θ2)×WSj

(7)

4 案例分析

4.1 西昌市及西昌轨道交通1号线基本情况

西昌市位于四川省西南部安宁河谷地区,境内由安宁河南北纵向贯穿全域,全境海拔在1 500 m以上,整体地形以山地为主,城市建成区和主要可开发土地大部分位于河谷平坝区域(占总面积的16.4%),是典型的带状河谷型城市。

西昌市目前尚无建成或在建的城市轨道交通,根据西昌市相关综合交通发展规划,远期规划西昌市轨道交通1号线,长度约15.5 km,覆盖居民活动中心、医院、集散枢纽等重要的出行点,路线建成后将支撑引领西昌城市空间向高铁新城拓展、缓解城区交通拥堵。路线走向如图2所示。

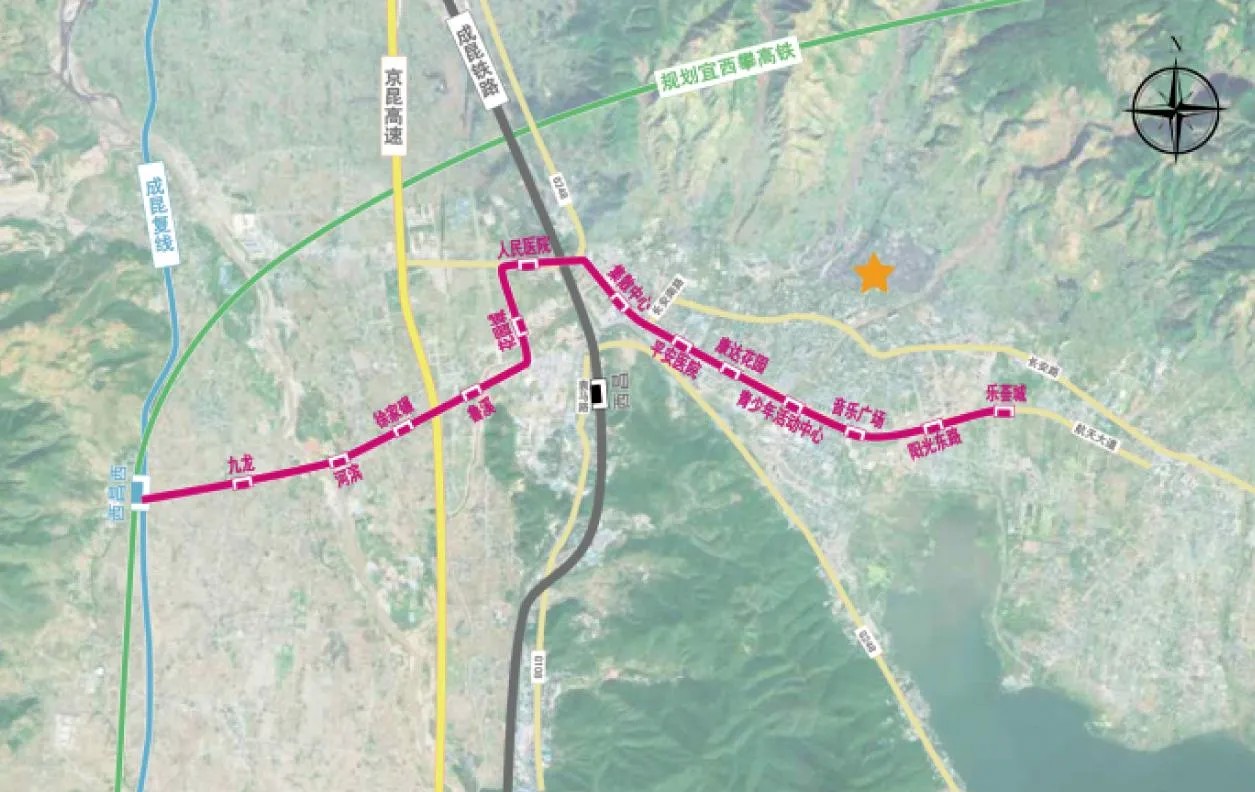
图2 西昌市轨道交通1号线路线走向示意Fig.2 Schematic diagram of the route of Xichang Rail Transit Line 1

4.2 具体分析

4.2.1 轨道交通制式初步分析

(1)中低运量轨道交通系统一般适用于常住人口在100万～300万之间的城市,2021年西昌市人口为96万人,结合近10年人口增长率、市内居民出行特征、公交系统客流量等数据,预计到2030年,西昌市人口将超过100万人,轨道交通1号线客流将达2.3万人次/d,达到《低运量轨道交通系统工程建设程序指南》[23]等相关文件要求。

(2)在制式要求方面,自动旅客捷运系统常服务于机场,悬挂式单轨目前在国内尚无建成运营的成功案例,不适用于西昌市轨道交通1号线的使用场景和西昌市经济发展情况,因此排除这两类制式系统。

4.2.2 算例验证

(1)利用层次分析法计算权重

Step1:构建层次结构模型。分别基于评价指标体系A、A′构建层次结构模型。以指标体系A为例,将3类、16项指标作为准则层,4类轨道交通制式作为方案层,如图3所示。

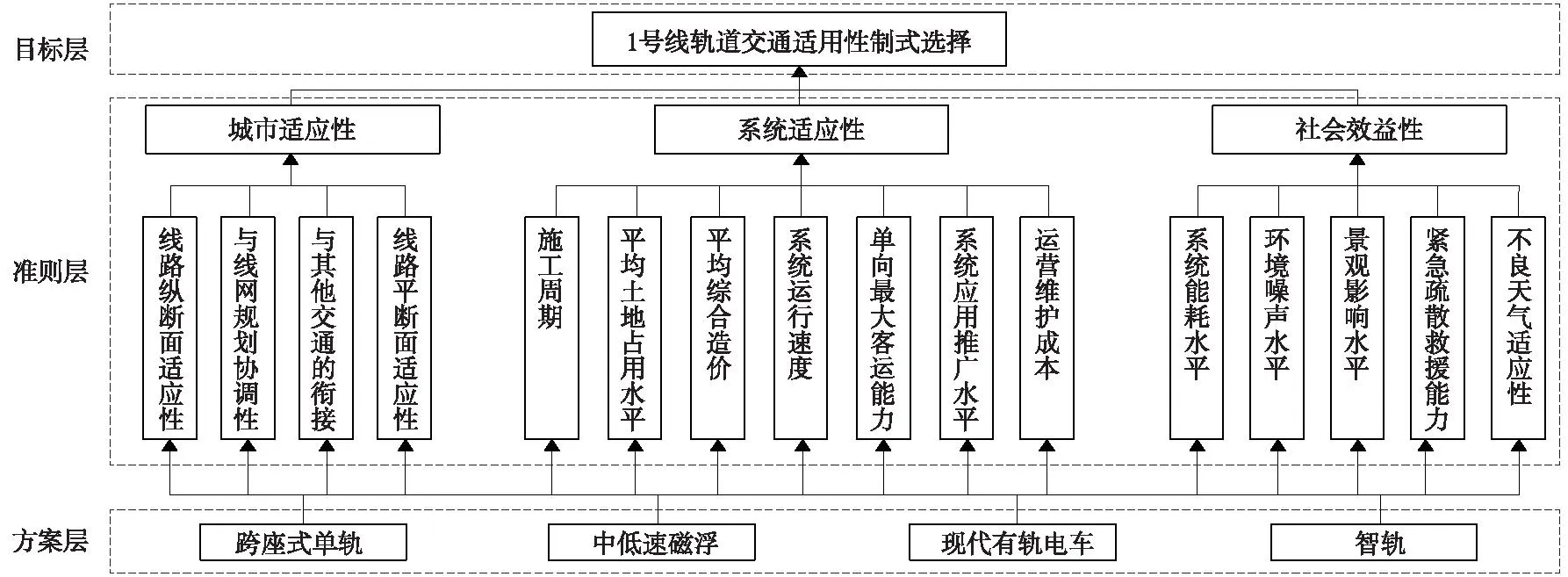
图3 基于指标体系A的层次结构模型Fig.3 A hierarchical model based on indicator system A

Step2:权重赋予。邀请中铁四院、凉山州交通运输局相关专家对层次结构模型赋予指标权重,形成判断矩阵。

Step3:一致性检验。通过计算,所有判断矩阵均通过一致性检验(RI<0.1)。以准则层中的城市适应性为例,判断矩阵和一致性检验如表5所示。

表5 判断矩阵及一致性检验示例Tab.5 Example of judgment matrix and consistency check

Step4:计算方案权重。对各层次指标权重进行加权,结果显示跨座式单轨、中低速磁浮列车、现代有轨电车、智轨系统的权重分别为WAj=[0.210,0.192,0.215,0.383]T、WADj=[0.253,0.167,0.208,0.372]T。

(2)仅考虑定量指标的熵权法

Step1:通过熵权法对各指标计算处理得到信息熵值、信息效用值和权重,详细数据见表6。

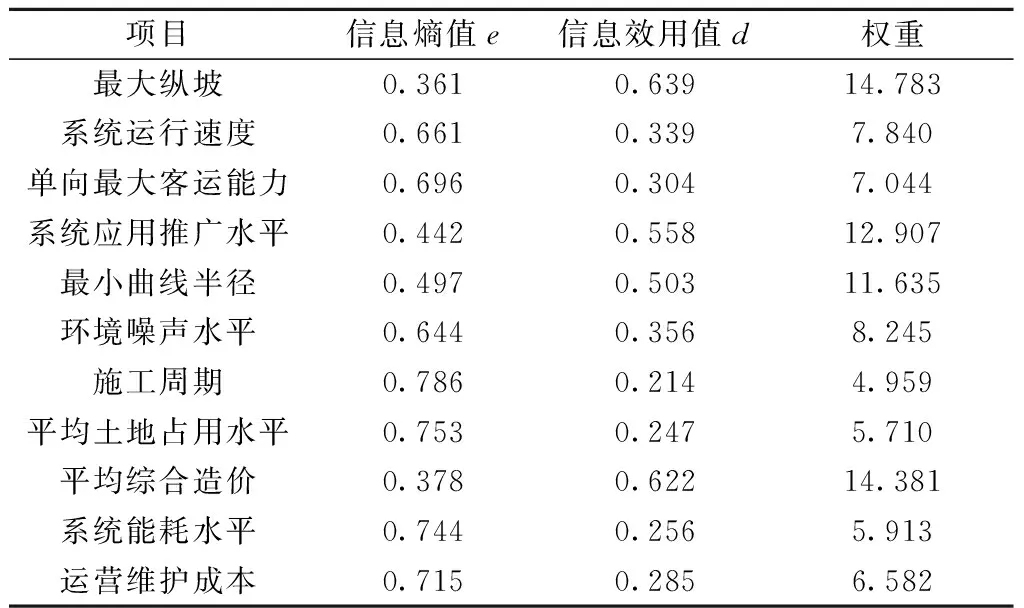
表6 信息熵值数据Tab.6 Information entropy data

Step2:根据各指标熵权法计算得到的权重,计算得出对跨座式单轨、中低速磁浮列车、现代有轨电车、智轨系统的综合评价得分,经过归一化处理,WSj=[0.197,0.184,0.220,0.400]T。

(3)引入主观偏好系数计算组合权重

评价指标体系A较A′更加完善、蕴含信息更丰富,评价结果相对精准,因此赋予WAj的主观偏好系数为0.5;评价指标体系A′中全部为定量指标,熵权法可更好体现客观数据的支撑性,因此赋予WSj主观偏好系数为0.3;相应赋予WADj主观偏好系数为0.2;最终计算组合权重W=[0.215,0.184,0.215,0.386]T。

(4)结果

根据基于熵权-层次分析法的组合权重模型计算结果,智轨系统得分最高,是4种中低运量轨道交通制式中最适用于河谷型城市西昌市轨道交通1号线的一种类型。

5 结语

本文以河谷型城市为对象,从城市经济发展、客流特征、地质条件、生态环境等因素着手,系统论证选择轨道交通制式系统时的重要考虑因素,提出需重点考虑轨道交通制式的综合建设成本、使用场景、客流承载水平、爬坡能力以及能耗污染、土地占用、噪声污染等情况;研究提出适用于河谷型城市选择中低运量轨道交通制式系统的评价指标体系,引入主观偏好系数,构建基于熵权-层次分析法的制式选择模型;以西昌市为例进行实例分析,形成了一套完整可靠的制式选择决策方法,填补了针对河谷型城市选择中低运量轨道交通制式的研究领域空白,可为相关部门提供决策支撑。

本文的研究成果为相关领域研究奠定了一定基础,未来还可进一步拓展中低运量轨道交通制式研究范围,深化完善评价指标体系构成,针对如盆周山区等更多山地城市开展轨道交通相关研究,支撑非平地地区的经济社会发展。