基于切换拓扑的量化时滞网络有限时间H∞控制

马 迪，李晨松

（内蒙古民族大学数学科学学院，内蒙古 通辽 028043）

近几十年来，动态网络得到广泛应用，比如电网、神经网络等。动态网络可看作是由许多时变节点连接形成的网络，节点的耦合普遍存在时滞，文献［1］研究了时滞网络的同步问题。网络有时会有外界干扰，当外界干扰存在时可以采用H∞控制的方法，文献［2］研究了状态依赖的非线性切换系统有限时间的H∞控制，文献［3］研究了具有扰动的非线性二阶多智能体系统的事件触发H∞有限时间一致性控制。

为了使网络性能更好，可以采用切换来改变节点间的拓扑连接方式，文献［4］研究了切换拓扑的复杂动态网络的指数簇同步，此外，数据传输是通过数字网络链路进行的，由于传输宽度的限制，数据信息在传输之前量化为有限位数也是一个提高性能有效的方法，文献［5］研究了非线性系统的量化自适应控制。量化和切换拓扑的方法使得系统不是右连续的系统，通常要考虑微分包含理论，文献［6］基于微分包含理论研究了有限时间协调控制。然而利用微分包含理论，在切换拓扑下对具有量化的时滞网络的H∞控制研究很少。本文的工作是：1）在切换拓扑下，设计量化控制器使得时滞动态网络在无外界干扰时有限时间稳定；2）在有外界干扰时，用相同的量化控制器和切换信号，此网络具有有限L2增益。

1 预备知识

定义1［1］→ξ表示对数量化函数，表示为：

其中ξ={±ξi,ξi=ρiξ0,i=±1,±2,…} ⋃{±ξ0} ⋃{0 } ,ρ∈( 0,1),ξ0＞0，ρ称作量化密度，并且对于任意的ι，可得到下面性质：

其中Δ ∈[-δ,δ] 是量化误差。

定义2［7］考虑一个向量微分方程

其中向量场f(x,t):ℛn×ℛ →ℛn，设Filippov集值映射K[f](xi(t),t):ℛn×ℛ →ℛn，定义

定义3［6］令V:ℛn→ℛ 是局部Lipschitz函数，Clarke广义梯度∂V:ℛn→ℬ(ℛn)定义为

其中co为凸壳，ΩV为V不可微点的集合。在x处，V相对于f的集值李导数LfV:ℛn→2ℛ定义为：LfV={a∈ℛ|∃v∈f(x),ζTv=a,∀ζ∈∂V(x)} 。

2 问题描述

考虑由N个节点构成的动态网络，每个节点的动态方程为

其中xi(t)=(xi1,xi2,…,xin)T∈Rn表示节点状态，f(xi,t)表示可微的向量函数，c是节点间耦合强度，Z=(zij)N×N表示外部耦合矩阵，Γ=diag(r1,r2,…,rn)表示内部耦合矩阵，d＞0 表示常时滞。uiσ(t)表示切换控制输入，其中σ表示切换信号在M={1,2,…,m} 内取值。gi为常数表示外部干扰强度，wi(t)表示外部干扰，ℐ={1,2,…,N}是指标集。

假设1假设Z满足零行和条件：，其中

设s(t)=(s1(t),s2(t),…,sn(t))T∈ℛn是s˙(t)=f(s(t),t)的解，并定义ei(t)=xi(t)-s(t)，yi(t)=ei(t)，=f(xi(t),t)-f(s(t),t)，误差系统的动态为：

为了提高传输速度而引入量化器，系统重写为：

由于系统（3）为右端不连续的系统，因此将系统（3）写成微分包含

假设2存在一个正常数θ使得非线性函数f:ℛn→ℛn满足：

定义4［1］当w=0 时，存在T＞0 使得当t＞T时，‖(e(t)) ‖≡0；那么系统（3）称为有限时间稳定。

定义5［14］如果存在非负常数γ和c，对于任意T＞0 和w(t)∈ℒ2[0,+∞]，满足

那么系统（3）具有有限ℒ2增益。

笔者研究系统（3）的有限时间H∞问题：设计状态依赖的切换信号σ(e)与每个节点的量化控制器uσ(e)，使得下面条件分别成立。

1）当外界干扰w(t)=0 时，系统（3）在有限时间内稳定；

2）当外界干扰w(t)≠0 时，系统（3）有限ℒ2增益。

为了研究上述问题，引用了如下引理：

引理1［1］对给定矩阵G1,G2,G3和常数ε＞0，

引理2［9］对任意向量x1,x2,…,xN∈ℛn，存在一个实数0 ＜p＜2 使得

成立。

引理3［10］对任意向量x,y∈ℛn，ε＞0 和正定矩阵Q∈ℛn×n，下面不等式成立：

引理4［11］对任意ωi≥0(i=1,2,…,n)，α1＞1，0＜α2≤1，下面不等式成立：

引理5［13］对于每一个x∈ℛn，如果其中θi≥0，那么

其中Ωi={x∈ℛn|xTQix≥0} 。

引理6［6］令Q⊂ℛn为包含原点的开集，考虑微分包含（1），如果存在连续可微函数V(x):ℛn→ℛ≥0和正定连续函数r:ℛ≥0→ℛ≥0，其中r(0)=0 ，满足maxLfV(x)≤-r(V(x)),∀x∈Q，且对于所有的ε＞0 ，有，那么微分包含是有限时间稳定的且有限收敛时间满足

3 主要结果

误差系统（3）的量化控制器设计如下

将式（5）代入式（3），可得闭环系统：

用前面定义的向量，闭环系统写为微分包含：

其中K=diag(k1,k2,…,kN)。

定理1若系统（6）满足假设1，且存在正定对角矩阵K使得

成立，其中α11=2θIN⊗Γ+c(ZZT)⊗(ΓΓT)+δ2ε-1(KKT)⊗In+εINn-2K⊗In，α22=c(1+δ2)INn，设计状态依赖的切换信号，则系统（4）H∞问题可解。

证明令由状态依赖切换信号，所以

（1）当w(t)=0 时，构造李雅普诺夫函数：，在Ωi内，V的集值李导数为

其 中 π(t)=diag(π1(t),π2(t),…,πN(t))，πi(t)=diag(Δi1(t),Δi2(t),…,Δin(t))，Δik(t)∈[-δ,δ]，k=1,2,…,n，i∈ℐ，，其中

令G2(t)=π(t)δ-1，G1(t)=e(t)，G3(t)=δeT(t)()-K⊗In，显然

于是由引理1可得到

即：

在上式两边加-2eT(t)(K⊗In)e(t)可得到

由假设2可得到

由Li⊗Γ＜0，可得到

由引理2可得到

由式（11）～式（13）可得到

即maxLq^V≤-2ηr(V(t))，其中，又因为V是连续的，由引理6 可得系统在有限时间内同步。

（2）下面证明w(t)≠0 的情况。由定理条件（7）可得到

即

而此时V的集值李导数满足下面不等式

所以

由e(t)是绝对连续函数，故V(t)=eT(t)e(t)也是绝对连续函数，因此于是有

由于V(t)＞0，令V(t0)=c，可得

由定义4可知，系统为有限ℒ2增益。

注释：定理中的矩阵不等式可利用Schur补引理写成线性矩阵不等式条件

4 数值仿真

考虑由5个节点组成的动态网络系统，每个节点动态方程为

其中，令s(0)=(-7,5,-2)T，对数量化器的参数ξ0=1，δ=0.1，内部耦合矩阵Γ=diag(0.3,0.1,1)，外部耦合矩阵为

c=1，w(t)=1+0.01 sint。仿真结果如图1～图4。

图1 无外界干扰时每个节点的轨迹Fig.1 The trajectory of each node without external interference

图1显示无外界干扰时每个节点的轨迹，分别表示xi1,xi2,xi3,i=1,2,…,5 的轨迹；图2显示无外界干扰时误差系统的轨迹，分别表示的轨迹；图3显示有外界干扰时误差系统的有限增益图，其中γ=max{γi}；图4显示切换信号。由仿真结果可知，所有节点在无外界干扰时同步，并且误差系统在无外界干扰时有限时间内稳定，在有外界干扰时具有有限ℒ2增益。

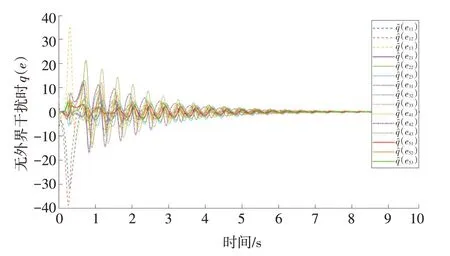
图2 无外界干扰时误差系统的轨迹Fig.2 The trajectory of the error system without external interference

图3 有外界干扰时误差系统有限L2增益稳定Fig.3 Finite L2 gain stability of error system with external interference

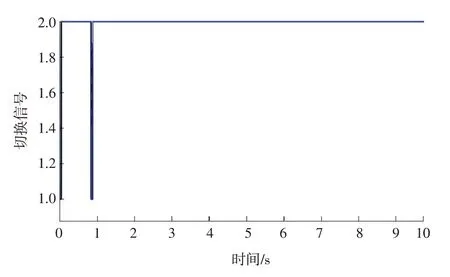
图4 切换信号Fig.4 The switching signal

5 总结

在切换拓扑下，通过设计状态依赖切换信号使得量化时滞网络在无外界干扰时所有节点有限时间内同步，且误差系统有限时间稳定，在有外界干扰时网络具有有限ℒ2增益，并且通过仿真例子验证了定理的有效性。目前有未知参数的自适应控制器应用广泛，今后会继续研究自适应相关问题。