Study on Dynamic Mechanical Behavior of Al-Mg-Si Alloy

TAO Xiaowang ,LIU Jibo ,LIU Xianbin ,CHEN Jianbin ,WANG Yonggang ,WANG Xiaofeng＊

(1.Key Laboratory of Impact and Safety Engineering,Ministry of Education,Ningbo University,Ningbo 315211,China;2.Ningbo Zhanci New Material Co.,Ltd.,Ningbo 315338,China)

Abstract: The dynamic mechanical behavior of Al-Mg-Si alloy was investigated under different strain rates by mechanical property and microstructure characterization,constitutive behavior analysis and numerical simulation in the present study.As the strain rate increases,the yield strength,ultimate tensile strength and elongation increase first,then remain almost constant,and finally increase.The alloy always exhibits a typical ductile fracture mode,not depending on the strain rate.However,as the strain rate increases,the number of dimples gradually increases.Tensile deformation can refine grains,however,the grain structure is slightly affected by the strain rate.An optimized Johnson-Cook constitutive equation was used to describe the mechanical behavior and obtained by fitting the true stress-strain curves.The parameter C was described by a function related to the strain rate.The fitting true stress-strain curves by the JC model agree very well with the experimental true stress-strain curves.The true stress-strain curves calculated by the finite element numerical simulation agree well with the experimental true stress-strain curves.

Key words: Al-Mg-Si alloy;strain rate;mechanical property;microstructure;Johnson-Cook model;finite element simulation

1 Introduction

Heat-treatable Al-Mg-Si (AA6xxx) alloys have drawn great attention from the automotive industry due to their high specific strength,good formability and excellent corrosion resistance[1-4].Considering that the demands of structural components and car body outer panels made of Al-Mg-Si alloys are increasing,it is important to know their mechanical properties.However,understanding only the quasi-static mechanical properties is insufficient since cars may be subjected to medium strain rate loading,such as car crashes.Accordingly,it is essential to know the dynamic mechanical properties of Al-Mg-Si alloys.

Aluminum alloys are considered to possess low strain rate sensitivity[5].Vilamosaet al[6]suggested that three different Al-Mg-Si alloys exhibit negligible strain rate sensitivity at room temperature.Chenet al[7]also revealed that two Al-Mg-Si alloys exhibit low strain rate sensitivity over a wide range of strain rates.Smerdet al[9]found that there is a very low and slightly positive increase in flow stress with strain rate in AA6082 alloy.However,some studies[9-13]have shown that the strain rate dependence of the mechanical behavior of aluminum alloys is affected by the chemical composition and strain rate,and when the chemical composition varies or the strain rate reaches a critical value,the strain rate dependence of the mechanical behavior may be significant.

In addition to tensile tests,finite element (FE)analysis should be performed to simulate the material’s dynamic response due to the high test cost of dynamic mechanical properties.One important aspect needed to acquire accurate simulation results involves suitable and realistic constitutive models at different strain rates that can be used in numerical analysis.The acquisition of the constitutive equation considering the strain rate effect is necessary,and their accuracy could significantly affect the simulation results.Many constitutive equations have been developed to characterize the deformation behavior under different loading conditions.In general,constitutive equations can be classified into two main categories: physically based and phenomenologically based,depending on their different assumptions.The former is established based on the deformation mechanism in which plastic deformation is actually a thermally activated process to overcome obstacles for mobile dislocations and is always complicated.The latter is based on empirical and semiempirical models that are relatively simple.Many models[5,14-16],such as Zerilli-Armstrong (ZA),Cowper-Symonds (CS),Khan-Liu (KL),Mecking-Kocks (MK),Molinari-Ravichandran (MR) and Johnson-Cook (JC),were proposed to describe the mechanical behavior in the past few decades.The JC model may be the most popular model due to its simple expression,and it fits the experimental results very well.

In this paper,to understand the dynamic mechanical behavior of Al-Mg-Si alloys,the effect of the strain rate on the mechanical properties and microstructure of Al-Mg-Si alloys was investigated first,and then the related parameters in the JC model were obtained to describe the relationship between the flow stress and strain rate.Numerical simulations of tensile tests at different strain rates were carried out to verify the accuracy of the parameters in the JC model.It is worth noting that to acquire accurate parameters in the JC model,tensile tests at ten groups of strain rates were conducted.Hopefully,the research could provide dynamic mechanical property results for the assessment of crash safety and application,understand the fracture mode and microstructure evolution,and obtain an optimized JC model for the improvement of simulation accuracy.

2 Experimental

2.1 Materials preparation

The received material was a cold-rolled Al-Mg-Si alloy sheet with a thickness of 1 mm,and its chemical composition was Al-0.7Mg-0.9Si-0.7Cu-0.3Fe-0.2Mn(wt%).To achieve a service state,the Al-Mg-Si alloy was subjected to the following treatments: solution treatment (555 ℃ for 2 min and then quenching in water),preaging (80 ℃ for 12 hours),natural aging(at room temperature for 14 days),prestretching (2%tensile deformation to simulate form processing) and artificial aging (170 ℃ for 20 min to simulate paint baking).

2.2 Mechanical property characterization

The mechanical properties were measured by quasi-static and dynamic tensile tests at a wide range of strain rates (10-3,10-2,10-1,1,10,50,100,200,500,and 800 s-1).According to plastic deformation theory,the strain rate was determined by the tensile velocity of the testing machine and the specimen gauge length.In addition,the strain rate could be expressed as:

where,Vis the tensile velocity of the testing machine andl0the initial gauge length of the tensile specimens.

The flow stress-strain behavior could be analyzed by the stress-strain curve.The engineering stressσEand engineering strainεEwere acquired according to the tensile tests.They are given by the following expressions:

where,Pis the tensile force,A0the initial cross-sectional area of the specimen and ∆lthe extension of the specimen.

According to engineering stress and engineering strain,the true stressσTand true strainεTcan be expressed as:

To compare the mechanical property difference between quasi-static tensile specimens and dynamic tensile specimens,the same specimen geometry was designed for the specimens.

The quasi-static tensile tests at a strain rate of 10-3s-1were performed by an Instron E1000 electrical tensile testing machine.The strain was measured by extensometer.To obtain the accuracy of the results,three sets of tests were carried out at this strain rate.

Dynamic tensile tests at different strain rates of 10-2,10-1,1,10,50,100,200,500,and 800 s-1were carried out by a Zwick-Roell HTM5020 high velocity hydraulic servo testing machine.Due to the high velocity of the tensile testing machine,the strain was obtained by digital image correlation (DIC) technology.Before tensile testing,nonuniform speckles were randomly sprayed on the gauge length of the specimen.During dynamic tensile tests,the variations in speckles were captured by a high-speed camera.Finally,the strain was analyzed by VIC-2D software according to the coordinate value of the lattice piece at each time step on the gauge length.Fig.1 shows the variation in speckle specimen gauge length at different time in the present study.The dynamic tensile tests were also repeated three times.

Fig.1 Observation of the tensile specimens at different time by high speed camera: (a) before testing;(b) plastic deformation state before necking;(c) after necking;(d) after fracture

2.3 Microstructure characterization

The microstructure was investigated using a Carl ZEISS Axio Imager A2 m optical microscope (OM).Longitudinal sections of the specimens were ground and polished according to standard metallographical techniques.The grain structure was revealed by etching in Keller’s reagent.

The fracture morphologies of the tensile specimens were observed by a Hitachi SU 5000 scanning electron microscope (SEM).The particle distribution of the Al-Mg-Si alloy sheet in the solid solution state was also analyzed by a Hitachi SU 5000 scanning electron microscope (SEM) equipped with X-ray energy dispersive spectrometry (EDS) systems.

To compare the microstructure differences between quasi-static tensile specimens and dynamic tensile specimens during tensile deformation,microstructural examinations were carried out.The observation area was in the vicinity of the fracture region due to the nonuniform strain distribution in the parallel segment.The microstructure in the vicinity of the fracture regions of the tensile specimens at different strain rates was also characterized on a Carl ZEISS Axio Imager A2 m optical microscope.

3 Experimental results

3.1 Mechanical property characterization

The engineering stress-strain curves of the Al-Mg-Si alloy under the different strain rates are shown in Fig.2(a).As clearly shown,all the curves are different,implying that the strain rate has some effects on the mechanical behavior.At the elastic deformation stage,the elastic modulus varies with the variation of strain rate,which is likely attributable to the inertia effect.At the plastic deformation stage,the specimens exhibit strain rate sensitivity in which the flow stresses are different at the same strain.However,the strain rate sensitivity is determined by the strain rate.When the strain rate increases from 10-3to 10-2s-1,the flow stress increases evidently;when the strain rate is in the range of 10-2-200 s-1,the flow stress changes slightly with increasing strain rate;when the strain rate exceeds 200 s-1,the flow stress increases appreciably with increasing strain rate.The corresponding true stressstrain curves obtained from Eqs.(2-5) also show the same trend,as presented in Fig.2(b).

Fig.2 Stress-strain curves of the Al-Mg-Si alloy sheet at different strain rates: (a) Engineering stress-strain curves;(b) True stress-strain curves

Strength and elongation are two important parameters that reflect the mechanical properties of materials.Variations in the yield strength and ultimate tensile strength with the strain rate are displayed in Fig.3.It can be observed that the relationship between the mechanical properties and strain rate is not monotonic.As the strain rate increases,the yield strength,ultimate tensile strength and elongation increase first,then remain almost constant,and finally increase.In contrast to quasi-static loading,dynamic loading is beneficial to improve the comprehensive mechanical properties of the alloy.It can also be learned that only a high strain rate can provide an appreciable strain rate effect.

Fig.3 Variation of strengths and elongation of Al-Mg-Si alloy sheet as function of strain rate

The strain rate sensitivity exponentmis a very important parameter to quantify the dependence of stress on the strain rate,which can be expressed by the following equation[17-19]:

where,σis the tensile stress andthe strain rate.Themvalue can be acquired through the logarithmic plots ofσversus.

According to the variation in yield strength with strain rate,the yield stress can be divided into three strain rate regions (region 1: 10-3-10-2s-1;region 2:10-2-200 s-1;region 3: 200 -800 s-1),as shown in Fig.3.The regions possess differentmvalues,and they are approximately 0.05,0.009 and 0.04 in regions 1 -3,respectively.

Based on the results,it can be concluded that the effect of the strain rate on the mechanical properties of Al-Mg-Si alloys cannot be ignored.

3.2 Fracture morphology

As is well known,fracture morphology can reflect the ductility of materials well.Therefore,the specimens at different strain rates may exhibit different fracture morphologies based on the elongation results.

According to the variation in elongation with strain rate,tensile specimens at four strain rates of 10-3,1,100,and 800 s-1were selected to observe the fracture morphology.Fig.4 presents the fracture morphologies of the specimens.All the specimens display a large number of dimples,which are the typical characteristic of the ductile failure mode.However,the fracture morphologies are also very different in detail in that the dimples gradually increase with increasing strain rate,which is consistent with the elongation results.Moreover,there are some cleavage facets known as the typical characteristic of brittle ductile fracture in the specimen at a strain rate of 10-3s-1,which provides evidence of the lowest elongation.

Fig.4 Fracture morphologies of tensile specimens at different strain rates: (a) 10-3 s-1;(b) 1 s-1;(c) 100 s-1;(d) 800 s-1

3.3 Microstructure characterization

The microstructure of the Al-Mg-Si alloy is displayed in Fig.5.Clearly,the microstructure is mainly composed of narrow elongated bands.Moreover,a larger number of secondary phase particles identified as Al(Fe,Mn)Si,Mg2Si,Q (Al1.9Mg4.1Si3.3Cu),and Si in the previous study[20,21]are along the rolling direction,which has a significant influence on microstructure evolution.

Fig.5 Microstructure of the cold rolled Al-Mg-Si alloy

Fig.6 shows the microstructure of the solution-treated Al-Mg-Si alloy.It is evident that the microstructure is completely different from the cold rolling microstructure.The grain structure is mainly comprised of equiaxed grains with an average grain size of approximately 21 μm.Moreover,some particles can still be observed in the alloy matrix.Fig.6(b) shows the particles distributed in the alloy more clearly.Only a few nonsoluble white particles were identified as Al(Fe,Mn)Si in the alloy matrix based on EDS analysis (Fig.6(c)).

Fig.6 Microstructures of the solution treated Al-Mg-Si alloy: (a)grain structure;(b) particle distribution;(c) EDS spectra of particle A

The following prestretching and aging treatment almost did not affect the solution-treated grain structure,mainly owing to the very small deformation and low temperature.Therefore,the final grain structure is similar to the solution-treated grain structure.

After tensile tests,the microstructure may have some changes.The tensile specimens at four strain rates of 10-3,1 100,and 800 s-1were also selected to compare microstructure differences.

Fig.7 shows the microstructure in the vicinities of the fracture regions of the tensile specimens.All the equiaxed grain structures are replaced by slightly elongated grain structures.Their average grain sizes are approximately 18-19 μm,indicating that tensile deformation could refine the grain structure and the effect of the strain rate on the grain structure is slight.

Fig.7 Microstructure in the vicinities of the fracture regions of the tensile specimens at different strain rates: (a) 10-3 s-1;(b) 1 s-1;(c) 100 s-1;(d) 800 s-1

4 Constitutive behavior analysis

As previously mentioned,phenomenological-based models are usually used to describe the deformation behaviors by considering the influences of work hardening,strain softening,strain rate hardening(or softening) and thermal softening.Currently,the JC constitutive model derived from experimental data rather than from physical principles is widely used because of its simplicity and accuracy.In addition,the JC model has been successfully embedded into many finite element programs for a wide range of strain rates and temperatures to describe the deformation behavior;thus,its application field is broadened significantly.The model assumes that the material is isotropic and introduces strain hardening,strain rate hardening and thermal softening.Its constitutive relation can be expressed as follows[5,12]:

where,σis the von Mises equivalent flow stress,εthe equivalent plastic strain,the equivalent strain rate,andthe reference strain rate;T*=(T–T0)/(Tm–T0),whereT0is the room temperature andTmthe melting temperature of the material;Ais the yield stress at a reference temperature and a reference strain rate,Bis the strain hardening coefficient andnis the strain hardening exponent;Candmare the material constants that represent the coefficient of strain rate hardening and the thermal softening coefficient,respectively.The above parameters can be calculated by fitting the true stressstrain curves under different strain rates.It is worth noting that the constitutive relation only describes the plastic deformation and does not include elastic deformation;therefore,the true strain in the constitutive relation is actually the true plastic strain.

To investigate whether thermal softening is present in the alloy,it is necessary to calculate the temperature rise on the basis of the portion of plastic work transformed into heat.The temperature rise could be expressed as[9]:

where,∆Tis the temperature rise,Cpthe specific heat capacity,ρthe density of the alloy,σthe true stress andεpthe true plastic strain.The parameterβis the fraction of the total plastic work that is converted into heat.

For aluminum alloy,Cp,ρ,andβare 900 J/(kg·K),2.7×103kg/m3,and 0.9-0.95,respectively.In the present work,the maximum strain rate of 800 s-1could result in the highest plastic work.Based on the integral of the plastic part of the true stress-strain curve (as shown in Fig.2(b)),it can be calculated that the plastic work is approximately 135 MJ/m3.Substituting the above parameters to Eq.(8),the temperature rise ∆Tis approximately 50 ℃.Obviously,the temperature rise is low,and thus,the thermal softening effect could be ignored.Accordingly,Eq.(7) was simplified and shown as follows:

ParametersA,B,n,andCcould be calculated according to fitting the true stress-strain curves.

In the present study,10-3s-1was taken as the referred strain rate.A,B,andncould be determined by the true stress-strain curve under the quasi-static tensile test,as shown in Table 1.

Table 1 Parameters of JC model of Al-Mg-Si alloy

When the equivalent plastic strain equals 0,the relationship between the dynamic yield true stress and the material strain rate is shown as follows:

The constantCwas obtained by the true stressstrain curves under nine other dynamic strain rates except for the referred strain rate.In addition,Cis summarized in Table 2.Different strain rates have differentCvalues.Obviously,it is not reasonable to average theCvalues as a result of the significant differences among theCvalues.An expression should be established to describe the variation in theCvalue with the strain rate sinceCwas affected by the strain rate.TheCvalue was determined by Origin 8.0 software and can be ex-pressed as follows:

Table 2 C value of JC model of Al-Mg-Si alloy

To verify the JC model,some representative true stress-true curves obtained from the model were compared with the experimental true stress-strain curves,as shown in Fig.8.In the low to medium strain rate regime (10-3-50 s-1),the true stress-strain curves fit very well.In the medium strain rate regime (100-800 s-1),although the true stress-strain curves in the low strain regime did not fit very well,those in the medium and high strain regimes fit very well.The somewhat difference between experimental and fitting curves in the initial stage of plastic deformation stage is mainly because that the predicted curves can not consider the stress oscillation.Despite this,the JC model can exactly reflect the constitutive relation of Al-Mg-Si alloys at different strain rates.

Fig.8 Comparison of true plastic stress-strain curves between experimental results and predicted results obtained from JC model at different strain rates:(a)10-3 s-1;(b)1 s-1;(c)10s-1;(d)50s-1;(e)100s-1;(f) 800s-1

5 Simulation of the tensile test

5.1 Damage and fracture criterion

To predict the effect of the strain rate on the true stress-strain curve,it is very important to simulate the tensile stress-strain curves and compare them with the experimental stress-strain curves.

The JC model considers plastic deformation,and damage and fracture should be considered in this part.It is well known that the damage and fracture criterion of Al-Mg-Si alloys could be based on the Johnson-Cook failure model.

When not considering the temperature effect,the fracture formulation can be expressed as[9]:

where,pandεeffrepresent the hydrostatic pressure and effective stress,respectively.

With respect to tensile deformation,ηequals-1/3.Accordingly,Eq.(11) can be modified as:

A strain rate of 10-3s-1was still taken as the referred strain rate.The equivalent ultimate plastic strains of the Al-Mg-Si-Cu alloy under different strain rates are summarized in Table 3.Applying the equivalent ultimate plastic strains,four constantsD1,D2,D3,andD4could be fitted using Origin 8.0 software,as revealed in Table 4.

Table 3 The equivalent ultimate plastic strain at different strain rates

Table 4 Parameters of JC failure model of Al-Mg-Si alloy

5.2 Tensile simulation

Finite element simulations were performed with the commercial FE code ABAQUS/Explicit.The complete simulation process mainly consists of modeling,material property input,step input,loading input,meshing,job submission and visualization analysis.The parameters of the JC deformation constitutive model and JC failure model were input into the material properties.The two sides of the tensile specimen were under clamped constraint and constant velocity loading.The tensile velocity could be calculated by Eq.(1).The finite element model of the tensile specimen is shown in Fig.9.

Fig.9 Finite element meshing of the tensile specimen

The simulation cloud maps of the tensile specimen at a strain rate of 10 s-1during the tensile test are presented in Fig.10.It can be observed that the true strain distribution is dependent on the stage of the tensile test;the true strain distribution is uniform before necking,while the true strain distribution is nonuniform after necking.After necking,the true strain is the highest in the vicinity of the necking zone.There is no doubt that the true strain distributions of other specimens at other strain rates are also nonuniform after necking.To obtain an accurate true stress-strain curve,a sufficiently large region including a large number of elements should be chosen for calculation due to the nonuniform true strain distribution after necking.

Fig.10 True strain distribution of the tensile specimen at a strain rate 10 s-1 during the tensile test: (a) before necking;(b) after necking

According to the average true stresses and strains of different elements,the true stress-strain at different strain rates could be calculated.Fig.11 shows the comparison of the representative experimental true stressstrain curve and calculated true stress-strain curve.Although the true stress-strain curve segments after necking between the tensile test and numerical calculation have a slight difference,the true stress-strain curves are still generally consistent,indicating that the simulation result is dependable.Therefore,to save the dynamic tensile test cost,simulation work is acceptable due to the relatively accurate simulation result.

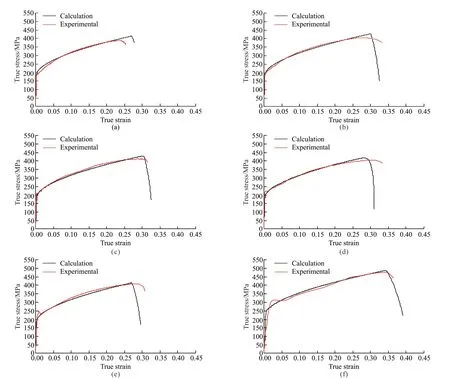
Fig.11 Comparison of true stress-strain curves between experimental results and simulation results at different strain rates: (a) 10-3 s-1;(b) 1 s-1;(c) 10 s-1;(d) 50 s-1;(e) 100 s-1;(f) 800 s-1

6 Conclusions

A study of the dynamic tensile behavior of Al-Mg-Si alloys was systematically investigated based on the detailed mechanical properties and microstructure characterization of Al-Mg-Si alloys under different strain states,constitutive behavior analysis and numerical simulation.The following conclusions are drawn from this study:

a) As the strain rate increases,the yield strength,ultimate tensile strength and elongation of the alloy increase first,then remain almost constant,and finally increase.Compared with quasi-static loading,dynamic loading is beneficial to improve the comprehensive mechanical properties.

b) The strain rate cannot affect the fracture mode,and all the specimens have the same ductile failure mode.However,the detailed fracture morphologies are significantly influenced by the strain rate.As the strain rate increases,the typical ductile fracture characteristics of dimples gradually increase.

c) The strain rate has almost no influence on the microstructure in the vicinity of the fracture regions of the tensile specimens.After the tensile tests at different strain rates,all the grain structures are comprised of elongated grain structures,and their grain size distributions are close.

d) An optimized Johnson-Cook constitutive equation considering the strain hardening effect and strain rate hardening effect was obtained by fitting the true stress-strain curves.The parameterCwas expressed by a function related to the strain rate.Generally,the fitting true stress-strain curves by the JC model agree well with the experimental true stress-strain curves.

e) The finite element numerical simulation under different strain rates was calculated.Overall,the calculated true stress-strain curves agree well with the experimental true stress-strain curves.It is reasonable to predict the dynamic mechanical properties of Al-Mg-Si alloys according to the established finite element model.

Conflict of interest

All authors declare that there are no competing interests.