Simulation of Dynamic Recrystallization in 7075 Aluminum Alloy Using Cellular Automaton

ZHAO Xiaodong,SHI Dongxing,LI Yajie,QIN Fengming,CHU Zhibing,YANG Xiaorong

(School of Materials Science and Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China)

Abstract: The evolution of microstructure during hot deformation is key to achieving good mechanical properties in aluminum alloys.We have developed a cellular automaton (CA) based model to simulate the microstructural evolution in 7075 aluminum alloy during hot deformation.Isothermal compression tests were conducted to obtain material parameters for 7075 aluminum alloy,leading to the establishment of models for dislocation density,nucleation of recrystallized grains,and grain growth.Integrating these aspects with grain topological deformation,our CA model effectively predicts flow stress,dynamic recrystallization (DRX) volume fraction,and average grain size under diverse deformation conditions.A systematic comparison was made between electron back scattered diffraction (EBSD) maps and CA model simulated under different deformation temperatures (573 to 723 K),strain rates (0.001 to 1 s-1),and strain amounts (30% to 70%).These analyses indicate that large strain,high temperature,and low strain rate facilitate dynamic recrystallization and grain refinement.The results from the CA model show good accuracy and predictive capability,with experimental error within 10%.

Key words: cellular automaton;dynamic recrystallization;7075 aluminum alloy;hot compression

1 Introduction

The 7xxx series aluminum alloys,known for their lightweight and high strength,are the materials of choice for aircraft structural components and are extensively used in the aerospace sector[1-3].The 7075 aluminum alloy,in particular,has enhanced strength due to the addition of precipitate-strengthening elements such as Zn,Mg,and Cu,but this also compromises its thermoprocessing capability.The influence of thermoprocessing on microstructural changes plays a pivotal role in determining the alloy's mechanical properties,highlighting the importance of controlling microstructural evolution during thermal deformation for optimal performance[4-6].Dynamic recrystallization,a frequent occurrence in plastic deformation,has been the focus of extensive research,particularly regarding its role during thermal deformation.Sunet alinvestigated the influence of thermal deformation conditions and second-phase particles on the microstructural evolution of 7075 aluminum alloy after deformation through hot compression experiments and quantitative metallographic tests[7].Li and team studied the thermal deformation behavior of 7085 aluminum alloy and found that the uneven distribution of Al3Zr diffuse phase contributes to promoting dynamic recrystallization[8].However,experimental methods are expensive and often fail to fully capture the dynamic recrystallization process.Advancements in computer technology have led to the application of various simulation models,such as phase-field[9,10],Monte Carlo[11,12],and cellular automaton methods[13,14],to simulate dynamic recrystallization in metals.These models are capable of calculating average grain size,recrystallization volume fraction,stress-strain curves,and can depict the evolution of microstructures.However,both phase-field and Monte Carlo methods have limitations in terms of computational volume and efficiency.In contrast,the cellular automaton method stands out by applying evolutionary rules to discrete spatiotemporal systems,offering considerable advantages in simulating dynamic recrystallization.

Cellular automaton methods have been applied to investigate the intricate microstructural evolution during the dynamic recrystallization process.Goetz and Seetharaman[15]pioneered the use of the cellular automaton method for simulating dynamic recrystallization,focusing on nucleation density,recrystallization kinetics,and strain rate effects.Huang and team[16]employed a mesoscopic CA model to simulate static recrystallization in 5754 aluminum alloy,particularly during a double-pass hot compression test.Zhang and colleagues[17]utilized the cellular automaton model to study 7055 aluminum alloy's microstructure during hot deformation,discovering that recrystallized grain size depends on strain rate and temperature,rather than initial grain size.Liu's team[18]created a novel CA model to simulate continuous dynamic recrystallization in 2219 aluminum alloy,especially focusing on the transition of subgrains from low-angle to high-angle grain boundaries.Mirdar and Serajzadeh employed artificial neural networks and cellular automaton methods to study the softening mechanisms of AA5083 at different deformation temperatures[19].Despite advancements in research,there exists a notable gap in the study of microstructure prediction concerning dynamic recrystallization processes in 7075 aluminum alloy.Previous investigations have predominantly concentrated on isolated factors influencing dynamic recrystallization,with insufficient attention given to a comprehensive analysis of deformation parameters such as strain,deformation temperature,and strain rate.Moreover,the incorporation of topological deformation in cellular grains has been overlooked,posing a challenge in accurately simulating the evolution process of grain dynamic recrystallization.Consequently,further exploration is imperative.

Our study investigated the dynamic recrystallization of 7075 aluminum alloy using isothermal compression tests,applying these results to develop and calibrate parameters for a CA model.We used this CA model to forecast the microstructural evolution during the hot compression of the alloy.The predictive outcomes of the established CA model were compared with the experimental results,demonstrating a high degree of consistency between the two.

2 Experimental

In this article,we conducted a series of isothermal compression tests on 7075 aluminum alloy to obtain material parameters for CA model.The chemical composition of the 7075 aluminum alloy (mass fraction,%)used in this research is detailed in Table 1.This alloy underwent a 24-hour homogenization treatment at 470℃,followed by air cooling.Cylindrical specimens with a diameter of 10 mm and a height of 15 mm were machined from the homogenized ingots.The experiments were carried out using a Gleeble-3800 thermal simulator,an advanced device widely used for simulating thermodynamic and mechanical processes of materials,with the corresponding experimental process illustrated in Fig.1.The experimental range covered temperatures from 573 to 723 K,with intervals of 50 K,and strain rates varied from 0.001 to 1 s-1,changing in tenfold intervals.The compression ratio of 60% corresponds to a true strain of 0.916.Specimens were heated at 10 K/s to the target temperature and then maintained for 3 minutes to ensure temperature homogenization.Thin graphite sheets were placed between the specimen and the punch to reduce friction with the mold.Additionally,a vacuum environment was maintained during the experiment to prevent oxidation.After compression,the samples were immediately quenched in water to freeze the microstructure.The processed specimens were cut along the central line parallel to the compression axis and characterized using electron back scatter diffraction (EBSD) and optical microscopy (OM) techniques to obtain information on dynamic recrystallization.

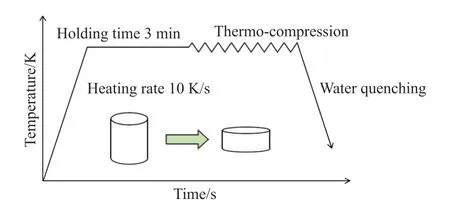
Fig.1 Flowchart of the simulated hot compression experiment process

Table 1 Chemical compositions of the 7075 aluminum alloy used in this study/wt%

2.1 True stress-strain curves

Fig.2 shows the stress-strain curves of 7075 aluminum alloy under conditions of strain rates ranging from 0.001 s-1to 1 s-1within a temperature range of 573 to 723 K.During hot deformation,flow stress is impacted by both work hardening and dynamic softening.Initially,at all strain rates,a rapid increase in dislocation density leads to significant work hardening,resulting in a quick rise in flow stress.At lower strain rates,dynamic softening becomes predominant after peak strain,gradually reducing stress until it stabilizes.For moderate strain rates,dynamic equilibrium between softening and hardening occurs post peak stress,maintaining stable stress levels.At high strain rates,the dynamic softening is inadequate to counterbalance work hardening,leading to a continued,albeit slow,increase in stress.Furthermore,higher temperatures and lower strain rates result in decreased peak and steadystate stresses.This phenomenon is attributed to higher temperatures promoting atomic diffusion and dislocation movement,thereby enhancing dynamic softening,while lower strain rates allow more time for the processes of dynamic softening and recrystallization.

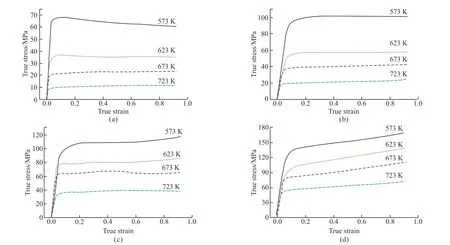
Fig.2 Stress-strain curves under different deformation conditions: (a) 0.001 s-1,(b) 0.01 s-1,(c) 0.1 s-1,and (d) 1 s-1

2.2 Consititutive model

In plastic deformation,deformation temperature primarily influences atomic diffusion and dislocation movement,whereas strain rate affects the rate of dislocation density accumulation and grain boundary energy.Hence,the peak flow stress is significantly influenced by both the deformation temperature and the strain rate.Sellars and Tegart[20]proposed that in the high-temperature plastic deformation of metals,the relationship among flow stress,strain rate,and deformation temperature can be described by a hyperbolic sine function,as follows:

where,represents the strain rate;A,A1,A2,α,β,nandn1 are constants determined by the material itself;σPis the peak stress (MPa);Qactis the deformation activation energy (J/mol),reflecting the difficulty of thermal deformation of the material;Ris the gas constant,R=8.314 J/(mol·K);Tis the thermodynamic temperature (K).

The value of α is calculated to be 0.0151 MPa-1using the following formula,where β andn1 are determined through linear fitting from Figs.3(a)-3(b).

Taking the partial derivative of both sides of Eq.(1) yields Eq.(5)

Dividing both sides of Eq.(5) by n and rearranging gives Eq.(6)

The values ofnandare obtained through linear fitting of Figs.3(c) and 3(d),thereby determining the value ofQact=141.767 kJ/mol.

Zener and Hollomon proposed that the stressstrain relationship in metallic materials,besides depending on the material itself,is primarily influenced by the deformation temperature and the strain rate.This relationship can be expressed by the Zener-Hollomon parameter,as shown in Eq.(7).

The value ofAis derived via linear regression from Fig.3(e),calculated to be 8.47×109s-1.The notable linearity in Fig.3(e) suggests that the relationship among flow stress,strain rate,and deformation temperature for 7075 aluminum alloy during hot deformation is aptly described by a hyperbolic sine function.

Fig.3 (a) ln-lnσp curves;(b) ln-σp curves;(c) ln-ln[sinh(ασp)]curves;(d) ln[sinh(ασp)]-1 000/T curves;(e) lnZ-[sinh(ασp)]curve

In summary,the constitutive equation for 7075 can be expressed as follows:

3 CA model

The cellular automaton is a dynamical model in which time,space,and states are all discrete.Its characteristic feature is that spatial interactions and temporal causal relationships are confined to the local vicinity.Such models are adept at simulating the spatiotemporal evolution of complex systems.

3.1 Dislocation density evolution model

In the hot deformation of metals,energy from the external environment is stored as dislocations,with higher dislocation density signifying increased energy storage.Dislocation density during deformation,which influences work hardening and dynamic softening,is characterized by the KM equation[21],detailed in Eqs.(9)-(11).

where,ρis the dislocation density,εis the strain,k1is the hardening coefficient,k2is the softening coefficient;θ0is the work hardening rate,andσsis the saturation flow stress,determined from the stress-strain curve.

3.2 Nucleation model

With increasing deformation,there is a gradual rise in dislocation density.Nucleation begins at the triple junctions of grain boundaries and grains when dislocation density surpasses a critical threshold.DING and GUO's research[22]reveals a close correlation between nucleation rate,strain rate,deformation temperature,and activation energy,as detailed in Eq.(12).

whrer,Cis a material parameter,determined through the reverse analysis method[23];mis the strain rate exponent;andRis the gas constant.

The nucleation mechanism of dynamic recrystallization is closely related to dislocation density.In thermally deformed metals,nucleation at grain boundaries and triple junctions initiates dynamic recrystallization when dislocation density reaches a critical level,denoted as ρc,due to increased deformation.The critical dislocation density ρcis determined by the energy necessary for grain boundary nucleation[24],as illustrated in Eq.(13).

where,γmis the grain boundary energy of high-angle grain boundaries;lis the mean free path of dislocations;Mis the grain boundary mobility;τis the energy per unit length of a dislocation line.

where,μis the shear modulus;θmis the high-angle orientation angle,taken as 15°;vis the Poisson's ratio,taken as 0.35;Cis a constant,which is generally taken as 10 for most metallic materials;δis the thickness of the material's grain boundary;Kis the Boltzmann constant,K=1.38×10-23J/K;D0bis the grain boundary self-diffusion coefficient at absolute zero;Qbis the grain boundary migration activation energy;andc2is a constant,taken as 0.5.

3.3 Grain growth model

The growth of recrystallized grains is facilitated by the movement of grain boundaries from the recrystallized grains,which have lower dislocation density,towards matrix grains with higher dislocation density,due to differences in dislocation densities.Post-nucleation,the growth of recrystallized grains is driven by energy stored during deformation,reflected in the level of dislocation density.The growth rateViof thei-th recrystallized grain adheres to Eq.(18)[25].

where,fiis the growth driving force per unit area of thei-th recrystallized grain,which is expressed by Eq.(19).

where,ρmis the dislocation density of the matrix grain;ρiis the dislocation density of the recrystallized grain;diis the diameter of the recrystallized grain;γiis the grain boundary energy between the matrix and the recrystallized grain,which is calculated using Eq.(20).

where,θiis the orientation difference between the recrystallized grainiand its neighboring grains.

3.4 Topological deformation model

During hot compression deformation,grains undergo elongation and deformation.Accurately simulating these morphological changes requires considering the topological deformation of the cellular matrix.The deformation of the cellular matrix has two aspects: one is the size of the matrix,assuming the initial matrix is ana×bmatrix,which deforms into anm×nmatrix.The other aspect is the spatial transfer of specific cells.Consider a specific cell (a,b) at a true strain ofεtthenn=bexp(-εt) Based on the principle of constant area during deformation,mis calculated asm=ab/n.

4 Results and discussion

4.1 Establishment of dynamic recrystallization model

In this study,we use a two-dimensional square cellular space on the MATLAB platform.Each unit cell in this space is a square measuring 1 μm × 1 μm.The simulation process involves five specific control variables for each cell:

Orientation variable: This is used to distinguish between different grains.The orientation number,a randomly generated positive integer,ranges from 1 to 180.

Dislocation density variable: This represents the energy stored due to grain deformation.A cell's dislocation density rises continually during deformation.When a grain boundary cell's dislocation density reaches the critical level ρc,nucleation occurs based on nucleation probability.For cells undergoing dynamic recrystallization,their dislocation density briefly drops to ρ0,then rises with ongoing deformation.

Grain boundary variable: Defined as two layers of cells at grain junctions,this variable differentiates grain interiors (value 1) from boundaries (value 0).

Recrystallization count variable: This integer counts a cell's recrystallizations-starting at 0 for unrecrystallized cells,increasing by 1 with each recrystallization event.

Color display variable: This variable simulates the morphological features of recrystallized grains by displaying varying colors.

The model employs a 500×500 two-dimensional square cellular grid,corresponding to a physical area of 500 μm×500 μm in the simulation.The model accounts for equiaxed grain growth,primarily considering the influence of the nearest neighbors using the Von Neumann neighborhood type and periodic boundary conditions.Fig.4 presents a flowchart of the dynamic recrystallization simulation,which includes three main stages: input parameters,initial microstructure generation,and the simulation of dynamic recrystallization process.Table 2 lists the detailed parameters required for the CA model.WhereQactrepresents the deformation activation energy;Qbdenotes the grain boundary migration activation energy;bis the Burger's vector;stands for the shear modulus;Tmis the melting point;andD0bsignifies the grain boundary self-diffusion coefficient at absolute zero.In each step of the Cellular Automaton Simulation (CAS),the system exhibits varying grain boundary mobility and grain growth driving forces within the recrystallized grains.To ensure a reasonable correspondence between each CAS step and the actual deformation time increment,it is necessary to guarantee that at least one cell in the simulation system undergoes an orientation transformation,i e,the corresponding grain boundary moves by the length of one cell.

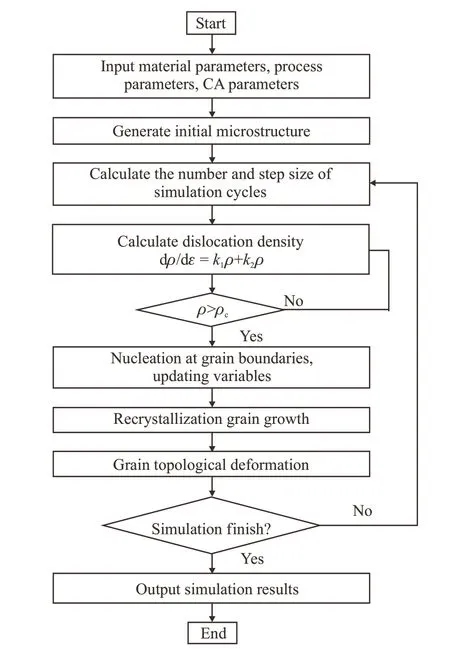
Fig.4 Flowchart of dynamic recrystallization simulation using the CA model

Table 2 Material parameters of 7075 aluminum alloy

In our study,we define the shortest time needed for a single cell to grow as the actual time corresponding to one step in the model,as outlined in Eq.(21)[26].

where,Vmaxrepresents the maximum grain boundary migration rate;LCAis the side length of a unit cell;Δfmaxis the maximum grain boundary migration driving force.According to the above equation,running one time step corresponds to the following increase in strain:

4.2 Initial organization

The 7075 aluminum alloy ingots require homogenization treatment prior to hot deformation,aimed at reducing the microsegregation phenomena occurring during the casting process and obtaining a supersaturated solid solution.Homogenization results in a uniform equiaxed grain structure with a consistent grain size.In the CA model,considering the average grain size observed in experiments is about 100 μm,nucleation points are calculated and uniformly distributed within the simulation area.These nucleation points grow in all directions with equal probability,developing the grains towards an equiaxed crystal direction.Fig.5 shows the initial microstructure of the 7075 aluminum alloy with average grain size about 100 μm (from 500 to 3000 steps).It is evident from the figure that,as growth steps increase,grains evolve towards a hexagonal equiaxed crystal structure.Fig.6 provides a comparison,revealing that the microstructure at 2500 steps aligns closely with the experimentally obtained microstructural photograph.Consequently,this study utilizes the microstructure achieved at 2500 steps as the initial state for the CA simulation of dynamic recrystallization.

Fig.5 Original microstructure at different growth step: (a) 500 steps;(b) 1 000 steps;(c) 1 500 steps;(d) 2 000 steps;(e) 2 500 steps;(f) 3 000 steps

Fig.6 Initial microstructure: (a) Experiment;(b) Simulation

4.3 Effect of deformation conditions on DRX

Utilizing process parameters from hot deformation experiments on 7075 aluminum alloys and established CA parameters,Figs.7(f)-7(j) presents simulated results depicting the microstructure at various deformation stages under conditions of 723 K and 0.1 s-1.It can be observed that the aspect ratio of the images changes with deformation,simulating the result of grain deformation after hot deformation.At 30% deformation,the original grains are slightly deformed,and fine equiaxed grains form at the grain boundaries.When the deformation increases to 50%,the coarser equiaxed grains are flattened and stretched,and newly formed grains continue to grow and elongate,forming a recrystallized structure.With further deformation,grains undergo more severe deformation,resulting in increased stored energy and dislocation density.As the dislocation density surpasses the dynamic recrystallization's critical threshold,nucleation initiates along the boundaries of the grains,followed by the growth and elongation of recrystallized grains,culminating in the formation of a recrystallized microstructure.Figs.7(a)-7(e) notably displays the microstructural evolution during hot deformation at 723 K and 0.1 s-1,where with increasing deformation,original grains elongate continuously,accompanied by an increase in stored energy and dislocation density.When dislocation density exceeds the critical threshold for dynamic recrystallization,nucleation at grain boundaries results in the growth and elongation of recrystallized grains,ultimately forming a recrystallized structure.Importantly,at equivalent levels of deformation,the EBSD photographs and simulation results show notable similarities.

Fig.7 Microstructures at different levels of deformation at 723 K and 0.1 s-1: (a)-(e) EBSD maps;(f)-(j) Simulations

Fig.8 illustrates that,across various strain rates,there is a fundamental consistency in trends of recrystallization percentage and grain morphology changes between experiments and simulations.With a reduction in the strain rate,there is an observed increase in the quantity of recrystallized grains,suggesting that reduced strain rates favor the alloy's plastic deformation and facilitate dynamic recrystallization.Conversely,at elevated strain rates,the formation of fine equiaxed grains is primarily observed at the boundaries and triple junctions of the initial grains.The shorter deformation time at high strain rates limits the full growth of these recrystallized grains.Conversely,at lower strain rates,the extended deformation time allows recrystallized grains to grow more with increasing deformation,progressively overtaking the original grains along the grain boundaries.This process results in straighter grain boundaries,reducing the stored energy.

Fig.8 Microstructures at different strain rates at 723 K: (a)-(d) EBSD maps;(e)-(h) Simulations

Fig.9(a) shows the curve of the change in recrystallization percentage with increasing deformation at 723 K and 0.1 s-1,where the recrystallization percentage gradually increases.Fig.9(b) presents the effect of different strain rates on the recrystallization percentage at a temperature of 723 K and a deformation of 60%,showing that an increase in strain rate leads to a decrease in recrystallization.Figs.9(c) and 9(d) show the changes in recrystallization percentage at different temperatures for strain rates of 0.001 and 0.01 s-1,respectively,indicating that higher temperatures promote the process of dynamic recrystallization.

Fig.9 Comparison of recrystallization fraction in experiments and simulations: (a) 723 K at 0.1 s-1;(b) 723 K at 60% deformation;(c) 0.001 s-1 at 60% deformation;(d) 0.01 s-1 at 60% deformation

4.4 CA model accuracy

Fig.10 illustrates a comparative analysis of the flow stress curves and grain size predictions from the CA model simulations alongside the experimental results,revealing a substantial concordance between the predicted and observed outcomes.As indicated by the stress-strain curve in Fig.10(a),during the initial deformation stage,flow stress rapidly increases,demonstrating linear work hardening and resulting in a marked rise in true stress.At a constant strain rate,rising temperatures aid atomic diffusion and dislocation slip at grain boundaries,diminishing grain boundary resistance to deformation,boosting thermal activation,and thus enhancing the alloy's dynamic recovery.With increased deformation beyond the critical strain,dynamic recrystallization commences.During this phase,dynamic softening and hardening occur alternately,new grains form continuously,and dislocation defects are repaired,leading to a dynamic equilibrium between softening and hardening,and ultimately stabilizing flow stress.Stress-strain curves predicted by the CA model align with experimental outcomes,suggesting that elevated temperatures foster dynamic recrystallization and contribute to the reduction of peak stress.

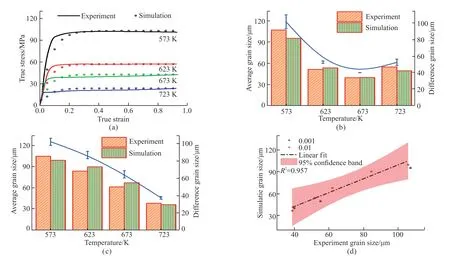
Fig.10 Comparison of experimental and simulation results: (a) Stress-strain curves at 0.01 s-1;(b) Grain size and error chart at 0.001 s-1;(c)Grain size and error chart at 0.01 s-1;(d) Comparison of grain size between experimental and simulation results

Fig.10(b) displays the average grain size in experiments and simulations under different temperature conditions at a strain rate of 0.001 s-1,where the relative deviations between simulation and experimental data are 10.9%,4.1%,0.3%,and 9.9%,respectively.In the temperature range of 573 to 673 K,the average grain size decreases with increasing temperature,as higher temperatures provide the necessary energy for nucleation and growth of recrystallization.At 723 K,the average grain size is about 10 μm larger than at 573 K,due to the higher temperature not only promoting recrystallization but also providing additional energy for grain growth,leading to grain coarsening.Fig.10(c)shows the average grain size in experiments and simulations under different temperature conditions at a strain rate of 0.01s-1,with deviations of 5.6%,7.0%,9.7%,and 5.5%,respectively,and the average grain size decreasing with increasing temperature.In comparing Figs.10(b) and 10(c) at temperatures of 623 and 673 K,it is observed that the lower strain rate of 0.001 s-1affords ample time for the nucleation and subsequent growth of new grains,culminating in a smaller mean grain size compared to that observed at a strain rate of 0.01 s-1.Nevertheless,at a temperature of 723 K and a strain rate of 0.001 s-1,the formation of coarser grains occurs,attributed to the elevated temperature facilitating grain growth by providing additional energy,and the reduced strain rate allowing extended time for this process.The comparison of recrystallization percentages and microstructure morphology under different strain rates (0.001 and 0.01 s-1) and temperatures (673 and 723 K),it is evident that the deformation temperature has a dual impact on grain size: on one side,elevated temperatures furnish the requisite energy for the nucleation and growth of recrystallized grains,resulting in a heightened percentage of recrystallization as temperature increases;conversely,these higher temperatures also accelerate the migration speed of grain boundaries and the growth rate of recrystallized grains,culminating in the development of coarser recrystallized grains.Fig.10(d) displays the correlation of the average grain size derived from both experimental and simulation data at 723 K and at strain rates of 0.001 and 0.01 s-1,achieving a fit coefficient of 0.957.The relative error remains below 10%,demonstrating the CA model's predictive precision.

5 Conclusions

Employing cellular automaton simulations alongside experimental methods,this research explores the hot deformation characteristics of the 7075 aluminum alloy,with particular emphasis on the impact of strain,deformation temperature,and strain rate on the microstructure.This yields the ensuing conclusions:

a) The activation energy for hot deformation of the 7075 aluminum alloy is 141.767 kJ/mol.The interrelation between flow stress,strain rate,and deformation temperature is expressed by the subsequent formula:

b) Dynamic recrystallization plays a pivotal role in the hot deformation process of the 7075 aluminum alloy.By establishing initial microstructures,a dislocation density model,and models for grain nucleation and growth,a mathematical foundation has been laid for simulating dynamic recrystallization using cellular automata.Both simulation and experimental results show that larger strains promote the process of recrystallization.Lower strain rates allow adequate time for the occurrence of dynamic recrystallization.Higher temperatures supply the necessary energy,yet excessively high temperatures may lead to grain coarsening when the deformation time is adequate.

c) The stress-strain curves predicted by the cellular automaton closely match the experimental results.The predicted dynamic recrystallization fraction and grain size have an error within 10% compared to the experimental data.These outcomes corroborate that the proposed model is proficient in precisely predicting the microstructural evolution occurring throughout the hot deformation process of the 7075 aluminum alloy.

Conflict of interest

All authors declare that there are no competing interests.