机载一维相扫雷达空域稳定算法研究

刘心成,张林让,张 涛

(1. 西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071) (2. 中国电子科技集团公司第二十七研究所, 河南 郑州 450045)

0 引 言

作为工程中常用的运动平台,相比较于固定平台,机载平台由于飞机偏航、横滚、俯冲、爬升等姿态变化或直线运动、转弯、悬停等运动状态改变,安装在飞机平台上的雷达波束指向也会随之变化,这时如果不采取保持天线扫描空域稳定的措施[1],极易造成天线波束偏离目标区域,进而造成雷达测量精度下降甚至目标丢失。

传统解决办法一般是为雷达天线安装硬件稳定平台,比如多轴陀螺,将雷达天线运动和载机运动隔离开;安装伺服稳定平台,通过闭合伺服回路使得天线波束指向不受载机姿态影响;文献[2]和文献[3]对机载伺服稳定平台系统进行了研究,介绍了伺服平台保持空域稳定的原理和设计思路。但是,硬件稳定平台存在体积大、笨重、造价高等缺点,控制精度和实时性也相对较差,因此未广泛运用[4-5]。

现在多采用电子稳定技术,即采用基于数据处理的波束补偿方法,通过分析平台机动或扰动引起的目标区域与载机之间空间相对关系的连续变化,解算出目标区域相对雷达阵面的指向角变化,通过对其补偿实现雷达波束稳定地指向目标区域。文献[6]和文献[7]探讨了机载雷达涉及的各种坐标系变换,却未探讨载机姿态或运动状态改变时波束指向角的变化规律。文献[8]和文献[9]研究了舰载相控阵雷达天线波束稳定照射的方法,讨论了波束照射空域稳定时涉及的坐标变换,但不涉及相控阵波束控制移相码的设计与计算方法。

文献[10-12]阐述了固定平台下相控移相码的设计、计算与工程实现,但不适用于运动平台,且缺少对波束指向精度的影响分析。文献[13-14]研究了数字移相器量化位数和量化误差对波束指向精度的影响,却未推导出定量的计算公式。文献[15]从波束覆盖的角度推导了一种相控阵雷达数字移相器位数的选取准则,却未探讨移相器位数与波束指向精度的关系。

综上所述,当前针对机载相控阵雷达保持相扫空域电子稳定的系统性研究论文相对较少。本文针对机载平台运动引起雷达天线波束指向角的改变以及由此带来的探测精度下降甚至目标丢失的问题,系统地探讨了机载雷达采用方位相扫、俯仰频扫和机扫相结合的方法保持空域稳定的波束控制方法,建立机载平台下指向角变换的数学模型,推导出由于机载平台运动引起波束指向角的变换公式,设计了方位相控扫描移相码的实现方法,并对相控扫描的关键技术指标进行仿真分析,设计思路对工程中机载相控阵雷达波束控制设计具有非常重要的参考价值。

1 空域稳定模型

天线波束的相控扫描是相控阵雷达的重要组成部分,相控阵雷达的波束控制流程是波束控制板接收主控计算机下发的指向角信息,通过实时运算或者查表的方式获得该波束指向下各移相器的移相值,然后驱动移相器移相,以实现天线各阵元的射频激励和接收信号的移相。当移相器移相值按照规律改变时,辐射到空间的波束指向随之改变,从而实现了天线波束的相控扫描。

本文以某型机载雷达为例,方位上相位扫描,俯仰上频率扫描和伺服机械扫描相结合,机载雷达波束控制的工作流程如图1所示,波束控制系统接收主控计算机下发的地理坐标系下波束指向角信息,波束控制系统根据惯导测量的姿态数据值计算出雷达阵面坐标系下方位和俯仰波束的指向偏角,并结合通过近场测试获取的雷达频率与俯仰指向的对应关系生成方位上移相控制码、俯仰上移频控制码和伺服控制码,控制移相器实现方位上相位扫描,控制频率和伺服实现俯仰上频率扫描和伺服机械扫描。

图1 机载运动平台波束控制流程

1.1 指向角变换

在雷达对目标的搜索、截获、跟踪和打击过程中,坐标系问题关系到载机运动补偿、波束稳定、波束预测、目标建航跟踪和显示等诸多问题。

雷达总体设计师通常给出地理坐标系下扫描空域的技战术指标,即波束俯仰角、方位角和扫描范围等信息,而波束控制设计师一般在雷达阵面坐标系下研究天线的扫描特性[16]。因此坐标变换是必不可少的技术环节。

机载雷达指向角变换一般需要经过以下步骤[17]：

(1) 由地理极坐标系变换到地理直角坐标系;

(2) 依次旋转载机航向角、俯仰角、横滚角得到载机坐标系;

(3) 载机坐标系平移,并依次旋转安装角、安装误差得到雷达阵面直角坐标系;

(4) 雷达阵面直角坐标系转极坐标系得到波束的驱动角。

建立地理坐标系O-XgYgZg,坐标原点O取在地面,Xg轴指向东,Yg轴指向真北,Zg轴铅垂向上,O-XgYgZg构成右手直角坐标系。地理坐标系下目标坐标矢量为OT,载机坐标矢量为OJ,那么雷达天线的最佳波束指向矢量为JT。

建立飞机载体坐标系Ob-XbYbZb,坐标原点Ob取飞机质心,Xb轴指向飞机右侧,Yb轴指向机头方向,Zb轴沿载体法线向上,Ob-XbYbZb构成右手直角坐标系。飞机载体坐标系与地理坐标系的关系可以由俯仰角、航向角和横滚角等姿态角来确定。

雷达与飞机平台采用刚性连接,初始安装时雷达载荷相位中心和一维俯仰伺服零点对齐,天线阵面法线方向与飞机载体坐标系平行,那么雷达阵面坐标系与飞机载体坐标系平行。

雷达工作时以地理坐标系下视角ψ进行方位向电扫描探测,下视角由主控计算机下发,雷达与照射区域几何关系示意图如图2所示。

图2 机载雷达波束照射区域几何图

定义角度如下：

(1)下视角ψ：地理坐标系下雷达和目标连线与水平面之间的夹角,由主控计算机输入雷达,机载雷达地面目标探测时下视角为负值;

(2)姿态角：由惯性导航测量后输入,包括航向角α,左航为正;俯仰角β,抬头为正;横滚角γ,右滚为正;

(3)目标方位角ε：地理坐标系下目标区域与机头在水平面的投影之间的夹角,左偏为正。

由此得到在地理坐标系下,飞机指向目标区域的方向矢量JT为

(1)

在雷达阵面坐标系下该方向矢量为

(2)

在雷达阵面坐标系下,雷达指向目标区域,天线波束方位角记为θ,天线波束俯仰角记为φ,那么得到波束指向角

(3)

方位角以飞机机头方向为零值,左偏为正,范围为-π～π,那么得到

(4)

特别地

(5)

俯仰角φ以机体坐标系XbObYb所在面为零值,向上为正值,范围为-0.5π～0.5π。

因此雷达方位相控扫描即是按照指向角θ进行移相码计算,下发给各移相器,驱动移相器移相,实现天线波束方位上对准目标。俯仰上雷达按照指向角φ进行频控和伺服扫描,根据天线设计师测量的工作频率与俯仰指向角的对应关系,在俯仰频率扫描无法指向目标区域时,控制伺服机械转动实现目标区域的俯仰对准。

由于坐标变换涉及矩阵乘法、正切等三角函数变换,更适合使用计算机或浮点数字信号处理器(DSP)进行计算。实际工程中可以由主控计算机计算完成后通过网络等接口下发控制码以减少硬件复杂性,当然也可以采用嵌入式浮点DSP计算。

1.2 移相码设计

方位上波束控制系统根据天线波束指向角θ,计算出天线各移相器单元的移相值,再转换为移相器的控制码,搭配移相器工作时序信号,驱动移相器进行移相,最终实现在指向角θ方向的定向辐射与接收。

1.2.1 阵元排布

方位上机载雷达采用一维均匀线阵在指定方向上的同相射频激励和接收,以实现空间波束的定向辐射和接收。

考虑N个阵元组成的一维均匀线阵[18],如图3所示,阵元间距为d,电磁波入射角θ,那么相邻两阵元之间电磁波延迟时间为

(6)

图3 阵列单元排布示意图

考虑到电磁波工作频率f,工作波长λ,那么由于时间差造成的相位差为

(7)

由式(7)可以看出,相邻两天线阵元对同一方向接收或者辐射的电磁波相位差是固定值,为工作波长和入射角θ的函数,调节阵元相位差值则θ也相应改变,进而控制天线波束指向特定方向,这就是通过相位控制实现波束扫描的原理。

考虑到工程中天线的加工、组件焊接、线缆不等长等误差,各个天线阵列收发通道之间具有幅相不一致性,记通道初始相位值φ0n,该值可以通过矢量网络分析测试得到。忽略温度变化、线缆反复弯曲等造成的相位变化,频点一定时该值是固定的,补偿幅相误差后,各个移相单元实际移相值为

(8)

1.2.2 移相码设计

工程中有源相控阵天线一般采用内部集成数字移相器的TR组件进行数字移相,移相范围一般为0～2π。假设移相器位数为k,那么其相移值是离散的,为最小相移理论值2π/2k的整数倍,因此数字移相器的移相步进和移相精度都受限于移相器位数,由此带来移相误差,进而对波束形成带来一定的性能损失[19]。

那么移相器理论移相值为

(9)

量化k为位控制码为

(10)

可见移相控制码是波束指向角θ、工作频率f、通道序号n、通道初始相位φ0n和移相器量化位数k的函数,其中波束指向角θ和工作频率f是变量,其他是常量。天线移相码计算就是在给定波束指向角θ和工作频率f的情况下,计算天线阵列各个移相单元(通道序号为1,2,…,N)的移相控制码。

1.3 移相计算的工程实现

移相器控制码的计算有多种实现方式,文献[20]采用查表法,即将所有波位和频点的组合对应的移相控制码预先计算好,存储在片上存储器中,然后根据频点和波位的索引进行查找,送到对应移相器上。查表法在控制规模比较小时方便快捷,但控制规模增大时所需存储量较大,且控制码传输时间过长;文献[21]采用DSP芯片架构实现,由于DSP程序顺序执行的特性,该方法多在小规模一维线阵中使用,此时配相码计算响应时间尚在可接受范围之内,且调试效率较高;也可以采用专用ASIC波束控制芯片[22],多用于批产项目,但灵活性差,且在研发阶段成本较高;采用现场可编程门阵列(FPGA)芯片架构,由于其丰富的DSP、IO、逻辑资源以及并行运算特性,成本和调试效率适中,非常适用于小批量生产或者试验验证项目中,本项目采用FPGA架构实现。

由前述公式可以设计出浮点运算的移相码,如图4所示。

图4 移相码浮点运算

移相码计算单元根据输入的频率和指向角索引得到相应的工作频率f和指向角θ,然后顺次相乘得到单通道相位、N个通道相位、初始相位补偿、取模、四舍五入,最后截取低k位即得到移相控制码。

浮点运算可以保证很高的运算精度,对运算缓存要求比较高,由于正余弦等非线性运算在各类处理器架构中都属于耗时非常大的运算,因此移相码浮点算法在运算实时性要求比较高时难以满足快速计算和波束扫描的需求[12]。

相比较浮点运算,FPGA更适合做定点运算,更适合实现简单规整的算法。为提高运算时效性,有必要将浮点运算转换为定点运算算法,并尽量简化运算过程,提高移相码运算效率,由此浮点移相码计算公式可以进一步化简为

(11)

可以看出,定点移相码的计算仍然涉及到正弦三角函数计、乘法运算、除法运算、取算及加减法运算,运算流程相对复杂,在FPGA中实现较为麻烦,同时也会消耗大量资源。为提升系统性能,有必要再次将定点移相码中的三角函数、乘法、除法、取模等运算进行简化,降低运算过程复杂度,FPGA算法优化后如图5所示。

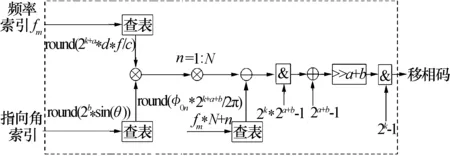
图5 移相码定点运算

其主要步骤有：

1) 将移相码计算中的浮点型数据转换为整型数据。其具体步骤为：

(1) 将算法中涉及的浮点型数据进行等比例放大,比如分别放大2a和2b倍;

(2) 将放大后的浮点型数据进行四舍五入处理,转换为整型数据。

2) 使用查表法简化运算过程。将预先可确定的乘除法运算值和正弦运算值进行整形处理后存入FPGA中ROM,省略掉复杂的三角函数运算并减少乘除运算环节,降低系统复杂度,提高运算速度;

3) 使用逻辑与、右移等操作简化取模、除法和四舍五入运算。在FPGA中将二进制补码值与模值按位逻辑与操作即可实现取模运算;将定点的二进制补码值加上0.5并右移就能实现除法和四舍五入运算;如此则省略掉运算中的分支判断和加减运算,大幅降低系统运算复杂度。

2 关键指标验证与分析

至此,完成了机载相控阵雷达保持方位波束电子稳定的移相码设计,实现了在当前运动姿态和状态下,对目标空域覆盖的波束控制,下面对天线扫描的关键技术指标进行验证分析。

2.1 移相码计算精度

移相码计算的精度与浮点数转定点过程中的四舍五入直接相关,当扩大倍数2a+b越大,则四舍五入的舍入误差越小,算法的计算精度越高。

以表1所示的阵列参数为仿真输入,FPGA定点运算和Matlab浮点运算结果进行对比,放大倍数2a+b与移相码计算误差关系示意图如图6所示。

表1 移相码计算仿真输入

图6 放大倍数与移相码计算误差的关系

由图6可以看出,随着放大倍数的增加,定点运算错误的比例在逐渐减少,当扩大倍数为240时候,FPGA计算结果与Matlab浮点运算结果完全一致,这一结果在图7～图8的仿真结果中得到验证。

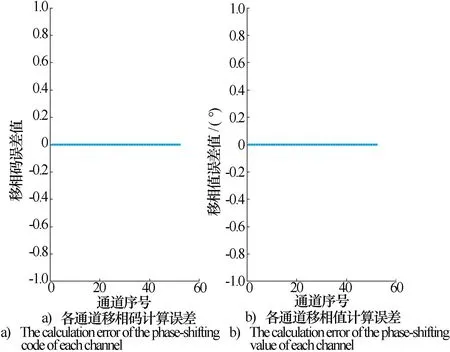
图7 放大240倍时所有通道的移相计算误差

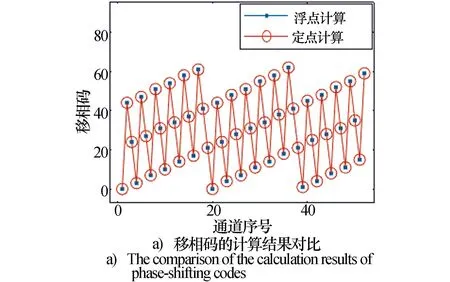
图8 放大240时某频点/波位所有通道移相码计算

图7仿真结果表明,在定点放大倍数为240时,所有输入频率和波位的组合下定点计算的通道移相码和移相值误差与浮点完全一致,误差为0。图8中结果表明采用定浮点计算的移相码和移相值完全一致。

2.2 移相码计算时间

移相码计算时间直接影响波束指向的转换速度,缩短移相码计算时间对提升雷达系统波束转换的实时性具有重大意义,特别是雷达工作于短时序、高数据率时对波束转换时间具有很高的要求。

进行N个移相单元的移相码计算,所需时间与通道计算时钟fN有关,所有通道移相码计算时间N/fN。以100 MHz计算时钟频率计算,完成52个移相单元的移相码计算时间仅为520 ns。

在FPGA中,还可以通过以下方式进一步缩短移相码计算时间：

(1) 通过提高计算时钟,进一步缩短移相码计算时间;

(2) 发射和接收移相码并行运算;

(3) 阵元特别多时,可以通过合理划分子阵,子阵间并行运算,子阵内顺序运算,从而缩短运算时间。

2.3 波束指向精度

由于采用数字移相器,k位移相器只能产生为最小相位2π/2k整数倍的相移量,因此移相值是离散的,不是任何相移值都能在数字移相器上准确地移相,由此将导致合成的波束指向与真实值产生偏差[23]。当采用FPGA定点运算,放大参数为a=b=20时,定点运算计算的移相码是无偏差的。如图9所示,采用6位数字移相器,仿真波束指向在-30°～30°范围内扫描时,可以看到波束指向误差小于0.06°。

图9 使用6位移相器的指向精度

2.4 移相器位数与指向精度的关系

数字移相器是现代相控阵雷达系统的必备部件,它的相位控制位数在很大程度上决定了相控阵雷达的造价、性能和设备的复杂性。因此在制定相控阵雷达方案时,合理地选择二进制数字移相器的相位控制位数是一个值得重视的关键问题。

数字移相器具有结构简单、低能耗、移相速度快、移相值稳定、控制电压低等优点,但它不能连续移相,由此存在相位量化误差[24]。相位量化误差一方面影响相控阵天线波束的主瓣电平,使得主瓣波束展宽,增益降低,降低了天线的抗干扰能力;另一方面影响了天线波束的指向,由于量化误差造成天线各移相单元实际馈电相位与理论值之间出现偏差,进而造成波束指向偏离理论值,造成指向误差,降低了天线波束的指向精度[25]。

由一维均匀线阵相位差与指向角的计算公式

(12)

对公式两边求导,得到

(13)

对于k位数字移相器,移相器理论移相最小步进值为2π/2k,移相精度小于最小步进值,那么得到

(14)

在不考虑其他误差的情况下,即得到由于移相器量化误差引起的指向精度理论最大值

(15)

可以看到,指向精度与指向角余弦及2k成反比,与电磁波工作波长成正比。以频率16 GHz为例,移相器位数分别为4、5、6,指向角为-30°～30°,仿真一维均匀线阵波束方向图指向精度,仿真结果如图10所示。

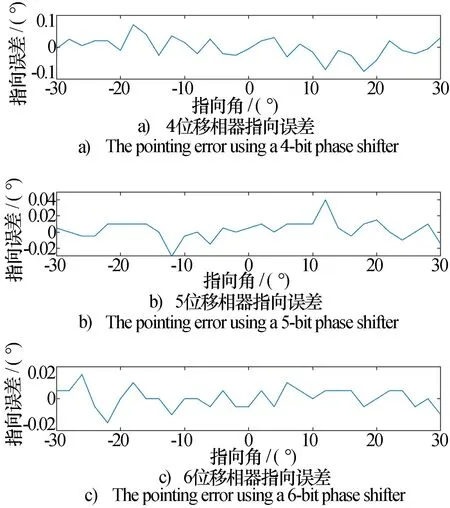
图10 移相器位数与波束指向精度的关系

可以看出,随着移相器位数的增加,波束指向精度也在提高,仿真结果与公式推导的计算结果在同一个量级,验证了移相器位数对指向精度影响的正确性。

2.5 空域稳定算法有效性仿真

机载平台由于偏航、横滚、俯冲、爬升等或直线运动、转弯等运动状态改变,目标区域与机载雷达的空间关系也随之连续改变,如果此时不采取保持天线扫描空域稳定的措施,极易造成天线波束偏离目标区域,并造成雷达测量精度下降甚至目标丢失。

采用表2参数对空域稳定算法进行仿真,解算出雷达波束指向角信息如表3所示。

表2 算法仿真输入

表3 算法仿真输出

通过仿真可以看出,在机载平台姿态角变化时,雷达波束的真实指向角已经改变。不采用空域稳定算法时,雷达波束将继续指向方位15°、俯仰-30°区域,此时雷达波束已经事实上严重偏离了目标区域,进而造成目标丢失。采用空域稳定算法时,首先解算出载机姿态变化后雷达波束的真实指向角(方位11.75°、俯仰-37.46°),由于俯仰角已经超出了频扫范围,因此需要根据频率与俯仰指向对应关系调整伺服角度实现俯仰波束的正确指向。方位11.75°仍在相扫范围之内,为相扫真实角度,直接将其生成移相码控制移相器进行移相,从而实现方位上目标空域的正确对准。

3 结束语

机载相控阵雷达是雷达发展的重要方向,当雷达在目标探测跟踪的过程中,由于平台姿态和运动状态的改变,造成雷达波束指向可能偏离目标甚至丢失目标,因此需要对雷达波束指向进行补偿以保证雷达波束指向的空域稳定。

本文对机载平台运动对波束指向角的影响进行数学建模,通过引入惯导测量的平台姿态信息对天线指向角进行实时修正与补偿,设计出天线波束相控扫描的移相码,并对波控控制的关键指标进行了仿真验证。结果表明,该算法可靠有效,计算精度和实时性高,设计思路可以推广到其他运动平台雷达系统中,对于运动平台雷达系统波控设计具有十分重要的参考意义。