基于多维信号特征的无人机探测识别方法

聂 伟 戴琪霏 杨小龙* 王 平 周 牧 周 超

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(中国民用航空飞行学院民航飞行技术与飞行安全重点实验室和电子与电气工程学院 德阳 618307)

1 引言

海洋事关国家安全和长远发展，世界上主要海洋国家将海洋权益视为核心利益所在，积极推行新一轮海洋经济政策和战略调整。随着我国海洋战略逐步从近海走向远洋、从区域走向全球，迫切需要具备全球海洋感知能力。当前面临的瓶颈问题是海洋目标的精细化探测与识别。同时，随着无人技术的快速发展，无人目标的出现为海上目标的探测和追踪带来了新的挑战。近年来，随着无人机(Unmanned Aerial Vehicle, UAV)技术的不断进步，无人机为海上监视[1]、海警巡逻[2]等工作提供了便利，并且伴随着视频转码技术的快速进步[3]，无人机能够实时、稳定地进行拍摄[4]极大地提高了无人机的海上侦察能力，这为维护海上安全提供了更多的手段。然而无人机在给人们的工作带来便利的同时也造成地安全隐患。一些不法分子利用无人机进行非法侦查、恶意攻击、走私等活动，对海上安全和航运业务造成潜在的威胁。因此，如何有效地探测和识别海上非法无人机，成为海上目标追踪领域中的一个重要课题。

在无人机探测领域，目前主流的探测手段是基于雷达回波信号[5]、无人机的声音信号[6]和光电信号[7]对无人机实现探测。文献[8]通过将无人机声音信号中的梅尔倒谱系数(Mel-Frequency Cepstral Coefficients, MFCC)作为特征，并利用不同环境下的声音信号与无人机声音信号融合进行数据增强，通过递归神经网络进行深度学习从而实现在不同环境下对无人机的探测。文献[9]提取无人机声音信号中包括MFCC和线性预测系数在内的5种特征，利用支持向量机算法进行分类识别。然而基于声音信号对无人机实现探测的方法受环境影响较大，当周围环境中拥有较大的噪声时会淹没无人机的声音信号从而对无人机的分类精度造成影响。文献[10]利用雷达的成像技术对无人机进行探测和定位。文献[11]使用调频连续波雷达，通过向无人机发射调频连续波，在一定范围内可以实现对无人机的探测。但是，由于无人机体积小、雷达截面积小，雷达无法精确探测，并且对于相同类型的无人机，雷达无法进行准确的区分。对于基于光电信号的无人机探测方法，是对无人机进行拍摄通过图像处理的方式对无人机进行探测。然而这类方法易受天气和光线遮挡等因素的影响，从而导致探测精度下降。综上所述，基于雷达回波信号，无人机声音信号和光电信号的无人机探测方法都会容易受到外界因素的干扰，在实际应用中存在局限性。而无人机通信信号作为无人机与地面交互的纽带，伴随着无人机工作的全过程，具有更强的抗干扰能力。此外，相比于无人机光电信号和声音信号，通信信号中包含了更多的能够表征无人机个体属性的信息，以通信信号中特征作为无人机的射频指纹能够更好地对无人机进行分类识别。因此，本文通过提取无人机通信信号中的指纹特征来实现对无人机的分类识别。

射频指纹的概念是由Hall等人[12]于2003年提出的，随后受到学者的广泛关注。射频指纹产生是设备在设计和生产过程中存在容差所导致的，射频指纹能够表征设备的个体特征，即使是相同型号同一批次的无人机也会存在差异，因此射频指纹具有唯一性且不易被篡改。此外，射频指纹在能够区分不同目标的同时还具有较高的鲁棒性和一致性，在不同的时间、不同环境下获取指纹特征具有一致性和可比性，这使得射频指纹在多种应用场景下依然能够作为对目标进行分类识别的依据。目前基于射频指纹的目标识别技术可分为两类即基于瞬态信号特征的目标识别和基于稳态信号特征的目标识别。文献[13]通过提取瞬态信号的小波特征对目标进行识别。文献[14]利用瞬态信号的稀疏表示作为指纹特征，实现对雷达辐射源识别。文献[15]对瞬态信号进行快速傅里叶变换(Fast Fourier Transformation, FFT)，基于瞬态信号的频谱提取特征来对无人机进行分类识别。虽然瞬态信号只与设备内部硬件有关能够表征设备的个体特征，但是瞬态信号持续时间短，不易被采集，对信号采集设备要求极高，大大增加了信号采集的成本。在基于稳态信号目标识别方面，文献[16]研究了辐射源稳态信号的星座图、功率谱等多个特征并分析了每个特征的性能。文献[17]提取稳态信号的星座图作为指纹特征，在信噪比为15 dB的环境下对ZigBee设备的识别率能达到93.8%。文献[18]提取信号中的置换熵作为射频指纹，能够分别对4个无线网卡的正交相移键控(Quadrature Phase Shift Keying, QPSK)调制信号和3个数字无线电设备的差分四相相移键控(Differential Quadrature Phase Shift Keying,DQPSK)调制信号进行识别，识别精确度能够达到95%。根据以上分析，通过提取无人机通信信号中指纹特征从而实现对无人机的分类识别的方法是可行的。

本文提出一种基于多维信号特征的无人机探测识别方法，本方法采用自适应三角阈值法从无线信号中检测到无人机通信信号并滤除噪声信号。通过提取无人机通信信号的盒维数和径向积分双谱(Radial Integrated Bispectra, RIB)作为无人机射频指纹，进一步采用主成分分析法(Principal Component Analysis, PCA)对RIB特征维数进行降维，在避免维数过高的同时，提高了无人机识别的准确度，从而实现对无人机的精确分类识别。此外，在检测到无人机信号的同时，同步解析无人机信号的信道状态信息(Channel State Information, CSI)，通过正交匹配追踪算法(Orthoganal Matching Pursuit, OMP)对无人机的方位角(Angle Of Azimuth,AOA)和俯仰角(Angle Of Elevation, AOE)进行参数估计，根据AOA和AOE的参数信息，建立定位模型对无人机实现3维空间定位。

2 信号预处理

本文基于软件无线电平台捕获监测区域的无线信号，获取的信号中既包含了有效的无人机数据又包含了无效的噪声数据，导致捕获的信号点数过多，这不仅会增加信号处理的难度，也会影响无人机的分类识别精度。因此需要一种方法将无人机信号从大量的无线信号中提取出来。本文利用自适应三角阈值法对无人机信号进行筛选。

自适应三角阈值法最早是由Zack等人[19]提出的，他们通过这种方法来获取图像的阈值从而将图像中主要物体目标筛选出来。自适应三角阈值法的主要思路是，在获取的信号中找到波峰，以波峰为起点向相反侧搜索寻找第1个不为0的点，将峰值点和不为0的点连成一条直线，并在两点间的每个柱体的顶部依次向直线做垂线，其中最长的垂线为选择的阈值。对无人机数据进行自适应三角阈值法预处理结果如图1所示。

图1 1倍阈值示意图

根据图1所示，红色的线即为阈值。可以看出通过自适应三角阈值法得到的门限值并没有完全滤除噪声信号，这是由于在实际的信号采集中，信噪比是波动的。因此1倍阈值无法完全对无人机信号进行提取，因此需要给阈值赋予权值。本文在信噪比为10 dB的环境对无人机进行探测，采用了1 000组数据每组2 500个点，其中环境数据为900组，无人机数据100组进行实验，分别对3倍阈值、5倍阈值和15倍阈值进行比较，比较结果如表1所示。

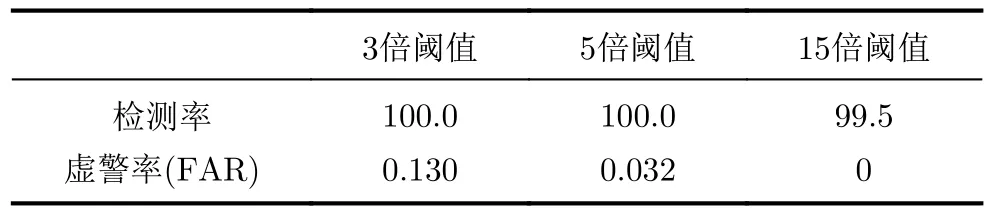
表1 不同权值检测结果对比图(%)

根据表1分析，5倍阈值时无人机信号的探测精度最高。因此，本文设置5倍阈值为筛选无人机信号的门限值，原始无线信号为2 500 000个点，经过预处理后信号点数为250 720个点，预处理前后无人机数据对比如图2所示。

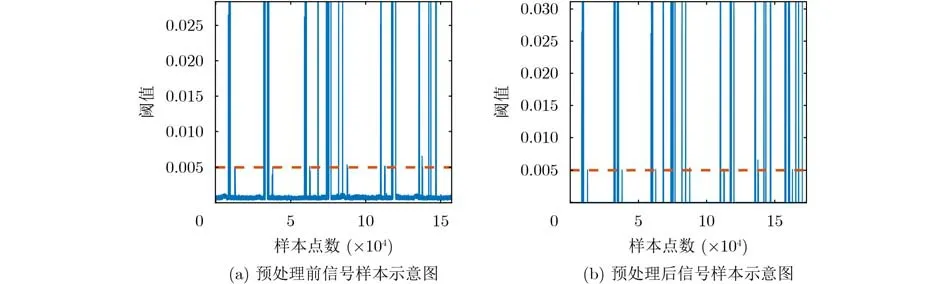
图2 信号预处理前后对比图

根据图2可以看出经过自适应三角阈值预处理后，大部分噪声信号被滤除，且数据点数也大大降低，这避免了后续的信号处理工作中由于数据量过大而导致计算困难的问题。

3 无人机定位

3.1 基于L型阵列天线的无人机定位

当检测到无人机信号后，无人机信号的 CSI会被解析出来，通过CSI可以估计出无人机的位置信息即无人机的AOA和 AOE。本文利用OMP算法对无人机的位置信息进行估计。本文选用L型阵列天线进行信号接收即x轴上阵元数为N的均匀线阵，y轴上阵元数为M的均匀线阵。此时，检测到K个无人机信源，以此可以构建阵列天线的方向矩阵，x轴上N个阵元的方向矩阵为

y轴上的M个阵元的方向矩阵为

综合x轴和y轴上的天线阵元可以得到L型阵列天线的阵列流型可表示为

根据以上公式接收的无人机信号可表示为

其中，s(t)=[s1,s2,...,sk]T表示K个信源向量，AL(θ,ϕ) 为阵列流型矩阵，n(t)为噪声。

通过将阵列流型矩阵AL(θ,ϕ) 扩展成Q维的过完备冗余字典G(θ,ϕ)，利用冗余字典将无人机信号稀疏处理即可得到

其中δ为Q维稀疏系数矩阵，通过求解式(8)方程即可得到AOA和AOE的估计值

3.2 无人机定位模型

本文部署3台接收机对无人机进行定位，每台接收机均采用L型阵列天线(即x轴N=3，y轴M=3)用于无人机信号的接收，通过OMP算法可以估计出无人机的位置信息，根据AOA的估计值和最小二乘算法可确定无人机在2维平面的位置

此外，根据得到的AOE估计值即可确定无人机的高度hi，3台接收机高度估计值的平均值被认定为无人机的实际高度，定位模型如图3所示。

图3 无人机定位模型

3.3 定位精度分析

Wireless InSite是一款用于电磁场仿真的软件，该软件可以分析室内、室外、城市等不同环境下无线电波的传输情况并且适用频率广泛。文献[20]基于Wireless InSite 软件对室内环境下无线局域网络(Wireless Local Area Networks, WLAN)信号的频段接收功率进行研究，通过与真实环境下实验结果对比证明了该软件的适用性，本文利用Wireless InSite软件模拟了一个 200 m×100 m的无人机飞行场景，场景中包含教学楼、树木、水池等，场景中物体的材质均与真实场景一致。在该场景中，设置3台接收机分别对飞行高度为20 m,30 m和50 m的无人机进行定位。

如图4(a)所示在无人机飞行高度为20 m时，3台接收机R1, R2和R3对AoA的参数估计误差分别为0.27°, 0.28°和0.26°，平均误差为0.27°，可见AOA的误差较小。而对于AOE的误差分别为0.89°,1.08°和1.12°，平均误差为1.03°，相较于AOA,AOE的误差较大。在定位方面，如图4(b)所示，定位误差随着置信度的增大而增大，整体上定位误差较小，3维定位误差相比于2维定位误差有明显的增大。为了比较无人机在不同飞行高度时对无人机的定位精度，因此本文以置信度为60%作为参考点。当置信度为60%时2维平面的定位误差约为0.33 m,3维空间误差约为0.7 m。

图4 飞行高度20 m定位误差示意图

如图5所示，当飞行高度为30 m时，3台接收机对AoA的估计误差为0.33°, 0.28°和0.27°，平均误差为0.29°，对AOE的估计误差为0.77°, 0.84°和0.64°，平均误差为0.75°。结合图4(a)，当无人机飞行高度上升时，对应AOA的估计误差有所增大，而AOE的误差则有一定的减小。根据图5(b)，当置信度为60%时2维平面误差约为0.34 m, 3维空间误差约为0.7 m。整体上，相比于飞行高度为20 m时，当无人机飞行高度为30 m时定位误差没有明显变化。

图5 飞行高度30 m定位误差示意图

如图6所示，当飞行高度为50 m时，3台接收机对AOA的估计误差为0.29°,0.3°和0.4°，平均误差为0.33°，对AOE的估计误差为0.45°, 0.56°和0.48°，平均误差为0.49°。结合图5(a)，当无人机飞行高度继续增加时，AOA的定位误差继续增大，而AOE的误差在持续减小。根据图6(b)当置信度为60%时2维平面定位误差约为0.3 m, 3维空间定位误差约为1 m。结合图5(b)相比于飞行高度为30 m时的定位结果，飞行高度为50 m时2维定位误差减小了0.04 m, 3维定位误差增大了0.3 m。因此，可以发现无人机飞行高度的增加会对无人机高度估计值造成影响从而导致2维定位误差变化较小，而3维定位误差具有明显的增大。

图6 飞行高度50 m定位误差示意图

相比于递归应用和投影多信号分类(Recursively Applied and Projected-MUltiple SIgnal Classification, RAP-MUSIC)算法，OMP算法使用迭代方法逐步选择最优的信号源位置，这种方法可以对信号源进行更加精确的定位，而RAP-MUSIC算法需要计算信号的空间谱，然后通过峰值检测确定信号源位置，因此对于信号源位置的估计可能会存在一定的误差。此外，由于OMP算法具有稀疏性，可以在较小的测量样本和较低的信号强度下实现较高的定位精度，而RAP-MUSIC算法利用了信号的空间特征，对于信号强度变化较大的情况下，定位精度相对较低。基于以上分析，本文利用OMP算法对无人机的位置信息进行参数估计，表2与表3对比了分别采用OMP算法和RAP-MUSIC算法的定位误差，比较结果如下。

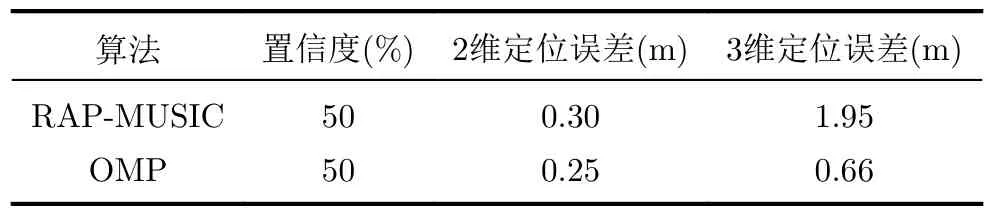
表3 飞行高度50 m算法对比图

根据表2和表3的结果可以看出，OMP算法的定位误差小于RAP-MUSIC算法的定位误差。RAPMUSIC算法是利用噪声子空间和通过构建空间谱函数，进行谱峰搜索从而实现对信号的参数估计的方法。OMP算法则是通过构造冗余字典将信号稀疏处理，然后对信号进行参数估计。OMP算法不需要进行空间谱估计，具有更低的时间复杂度[21]，更加适合实际应用。

4 基于射频指纹的无人机识别

当从获取的无线信号中检测到无人机信号时，根据无人机的CSI对无人机的位置信息进行参数估计，从而精准地确定无人机的位置。在确定无人机的位置后，提取无人机通信信号中的RIB和盒维数作为无人机的指纹特征，将两种指纹特征输入分类器中从而实现对无人机的分类识别。

4.1 盒维数特征提取

分形维数是一种描述信号自相似性和复杂性的度量指标。与欧几里得几何中的整数维度不同，分形维数可以是一个非整数，因此分形维数可以有效地表述信号在不同尺度下的形态特征。分形维数包括豪斯多夫维数[22]、信息维数、谱维数等。本文通过提取信号的盒维数作为指纹特征对无人机信号进行分类识别。盒维数提取方法如下：

(1)假设获取到长度为N的无人机序列y(1),y(2)...y(i)...y(N) ，其中i=1,2,...,N。根据信号长度确定格子的最大边长为

(2)使信号序列的最小值为0

(3)对x进行重采样使无人机序列等比例缩放得到新的序列，此时无人机序列的最大值为L，序列总点数为L+1。

(4)将边长为L的大方格划分成边长为ε的小方格，记录覆盖信号的小方格的数量为N(ε) ，对ε和N(ε) 进行拟合，拟合曲线的斜率即为盒维数D

本文分别对大疆的tello无人机信号序列和DJI Spark无人机信号序列，利用最小二乘拟合方法进行盒维数提取。如图7所示，其中红色线为tello无人机，蓝色线为DJI无人机。二者的拟合曲线具有明显的差异，最为明显的差别在于二者曲线的斜率不同，这也代表两款无人机的通信信号具有不同的盒维数。其中两种无人机分别以第50组无人机数据为参考，tello无人机的斜率为1.606 2，而DJI Spark无人机的斜率为1.530 1。为了进一步研究二者盒维数的差异将对更多的无人机数据提取盒维数。

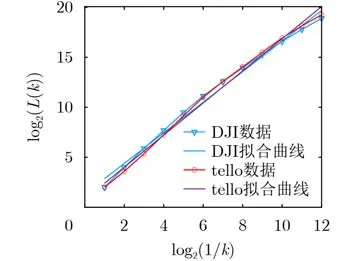
图7 tello和DJI无人机拟合曲线示意图

为了验证将盒维数作为无人机分类的指纹特征的可行性，本文提取了200组无人机信号(其中tello无人机100组，DJI Spark无人机100组)的盒维数。如图8所示，tello无人机信号的盒维数在1.58～1.62，Spark无人机信号的盒维数在1.51～1.55，两款无人机的盒维数值具有显著的差异，能够对两款无人机进行有效的区分。因此盒维数符合作为指纹特征的标准，能够根据无人机信号的盒维数实现对无人机的分类。

图8 无人机盒维数对比图

4.2 双谱特征提取

双谱能够定量地描述系统的非线性特性以及谱值中两个频率分量之间的关系。在实际应用中，双谱可以对噪声和干扰进行抑制与去除，具有较强的鲁棒性。此外，相比于高阶谱，双谱的计算量更小，维度特征更小。因此，本文选择将无人机信号的 RIB作为指纹特征实现对无人机的分类。高阶谱是k阶累计量的k-1维傅里叶变换。因此，高阶谱可表示为

其中，Cku表示无人机信号的k阶累积量。当k=3时可以得到双谱的表达式为

在实际应用中，由于信号采集设备只能采集有限的数据样本，因此只能近似地估计双谱特征值。目前对于双谱特征值的估计方法有两种，即参数估计法和非参数估计法。其中参数估计法是通过对信号进行建模来计算双谱，但是该方法建模困难。非参数估计法分为直接法和间接法，直接法是先对信号序列进行傅里叶变换，然后计算3阶相关从而求得双谱估计值。间接法是先对信号序列求3阶累积量然后傅里叶变换以此求得双谱估计值。直接法和间接法均能得到双谱估计值，本文选用非参数估计间接法来估计双谱值[23]，具体步骤如下：

(1)将无人机信号序列y(1),y(2),...,y(N)分成每段长度为K的序列，共分成P段，每段序列减去各段序列的均值使每段序列进行局部中心化，则第P段序列可表示为xp(0),xp(1),...,xp(K-1)，其中p=1,2,...,p。

(2)估计每段序列的3阶累积量

其中，K1=max(0,-l1,-l2),K2=min(K-1,K-1-l1,K-1-l2)。

(3)计算每段3阶累积量估计值的平均值即为无人机信号的累积量

(4)根据公式可以得到双谱估计值

其中，L ＜K-1,w(l1,l2)表示窗函数。

本文分别对DJI Spark无人机信号和tello无人机信号各取90组数据进行双谱估计，如图9所示，其中具有较大峰值的部分为无人机的双谱估计值，Spark无人机的归一化双谱值的频率分布在[-0.3,0.3]，而tello无人机的归一化双谱值的频率分布在[-0.1,0.1]，二者具有明显的差异。因此，可以根据无人机信号的双谱值来判断无人机的类别，但双谱值数据的维度较大不利于后续的机器学习。因此，本文选用数据维数相对较小的RIB作为无人机的射频指纹。

图9 双谱估计3维图

RIB是在双谱的频率平面上，沿着过原点的直线做积分运算，得到的双谱积分值即为RIB的值[24]。如图10所示，蓝色的点为双谱值，黑色虚线为积分路径。

图10 RIB积分路径图

当接收到预处理后的无人机信号后，根据式(17)可以求得B(f1,af1)，根据RIB公式即可求得径向积分双谱值

其中，a为非正态白噪声激励参数， 0＜a ≤1，f1为当前频率谱。

RIB同时具有时移不变性、尺度变化性和相位保持性等优点[25]，具有较强的稳定性，符合作为射频指纹的标准。然而，RIB数据维数依然过高，会对后续的机器学习增加计算量，因此需要对双谱值的维数进行PCA降维。

4.3 PCA降维

主成分分析法(PCA)是将m维的数据投影到n维空间，同时尽可能地保留原始数据的信息。PCA的降维过程是通过计算数据的协方差矩阵来实现的，协方差矩阵描述了数据之间的线性关系，而PCA的目标是找到这些关系的主要方向，这些方向即为主成分，它们原始数据的线性组合。PCA具体实施步骤如下：

(1)对输入的RIB数据D={d1,d2,...,dn}进行归一化处理，每个数据减去均值µ，并除以标准差σ，使得数据具有0均值和单位方差；

(3)对协方差矩阵进行奇异值分解，求得矩阵的特征值和特征向量；

(4)将特征值从大到小排列，并选取前k个特征向量作为主成分；

(5)将标准化数据映射到所选的主成分上，得到降维后的数据。

当贡献率设置为75%时无人机的识别精度为97.5%,96.2%和97.5%，当贡献度为85%时，识别精度均为100%，对比结果如图11所示。PCA在降低数据维度的同时，能够保证表征无人机个体属性的信息不丢失，本文将主成分的贡献率设置为85%，RIB的维数从128约简为99 。

图11 贡献率选择对比图

5 实验及分析

本文主要研究基于多维信号的无人机探测识别技术，实验选用大疆公司生产的Spark和tello系列无人机。两款无人机的带宽均为20 MHz，通过小米10手机对无人机进行控制。在信号采集方面，本文利用USRP X310搭配2.4 GHz定向天线和2.4 GHz全向天线进行信号接收，其中抛物面定向天线的接收增益均为17 dBi，全向天线的接收增益为10 dBi。

5.1 基于盒维数的无人机分类

本文对两款无人机采用决策树算法、加权K邻近算法(K-Nearest Neighbor, KNN)和线性支持向量机算法(Support Vector Machine, SVM)进行分类识别验证。其中，将120组无人机盒维数数据用来训练和80组数据用来验证，决策树算法中分裂数为20，加权KNN算法的邻近点数为10，SVM的核函数为线性核函数。通过实验，分类结果如图12所示，其中标签1为DJI Spark无人机，标签2为tello无人机，横坐标为分类器识别判定的类别，纵坐标为真实类别。根据图12可以看出3种算法的准确率均为100%。由此可见，盒维数在3种不同的算法中均有良好的分类效果。

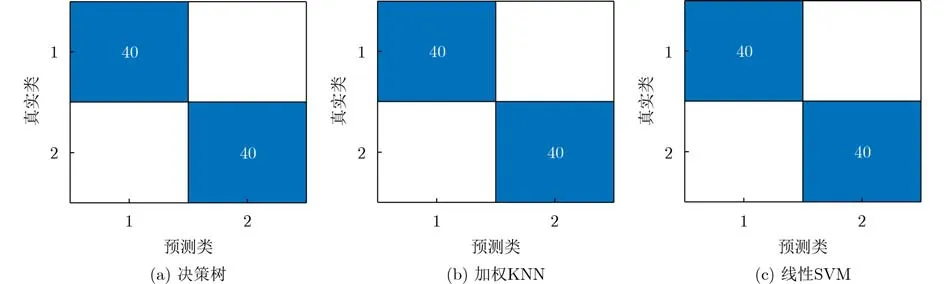
图12 分类结果示意图

5.2 PCA降维对径向积分双谱特征的影响

本文分别用决策树算法、加权KNN算法和线性SVM算法分别对降维前的双谱数据和降维后的双谱数据进行机器学习并进行验证，本文分别将两类无人机的RIB数据中的50组数据用于训练，40组数据用于验证。其中，决策树算法中分裂数为20，加权KNN算法的邻近点数为10，SVM的核函数为线性核函数。结果如图13所示，降维前决策树、线性SVM和加权KNN的准确率为98.8%, 100%和98.8%，降维后三者的准确率分别为100%, 100%和100%。PCA在降维的过程中，数据中的冗余信息会被移除，从而使数据降低到更少的特征维度到达数据压缩的目的。然而，PCA保留的主要方差方向对于原始数据中的信息贡献最大，而次要方差方向对信息贡献较小，因此PCA在减少冗余数据的同时，能够最大限度地保留信息的原始特征。本文利用PCA 对RIB数据进行降维，降维前特征维度为128，降维后特征维度为99，不仅特征维度得到约简，同时还提高了识别精度。

图13 PCA降维前后对比图

6 结论

针对非法无人机的探测和识别问题，本文提出一种基于多维信号特征的无人机探测识别方法。本方法首先通过自适应三角阈值法对捕获的无线信号进行预处理，将无人机信号筛选出来并降低数据量，同时获取无人机信号的CSI。然后，基于CSI利用OMP算法对无人机的位置参数进行估计，通过得到的参数信息，建立定位模型从而实现对无人机的精确定位。最后，提取无人机信号中的盒维数和RIB作为识别无人机的指纹特征，通过机器学习获取分类器从而实现对无人机的分类识别。实验表明，本文用到的定位算法能够精确地对无人机实施定位，定位精度小于1 m，并且利用该文选取的指纹特征对无人机的识别精度能够达到100%。