多目标跟踪中基于次模优化的轨迹片段生成方法

孙 瑾 杜官明

(南京航空航天大学民航学院 南京 211106)

1 引 言

多目标跟踪(Multi-Object Tracking, MOT)一直是计算机视觉领域一个非常活跃的研究课题，它是很多视觉任务的基础工作，例如智能监控、视觉导航和运动分析等，具有广阔的应用前景。相对于单目标跟踪，多目标跟踪过程中存在着目标数量和类型不确定、目标相互干扰和遮挡等复杂情况，导致跟踪过程中出现目标丢失、目标身份(IDentification, ID)频繁转换等问题。因此多目标跟踪问题也一直是一个具有挑战性的课题。

近年来由于目标检测[1,2]技术的巨大进步，基于检测的多目标跟踪技术(Tracking By Detection,TBD)取得了很多成果。TBD借助先进检测器获取每帧目标对象，基于对目标的位置预测，通过提取目标特征将相邻帧的同一目标关联以实现对目标的持续追踪。数据关联是其中最重要的环节，在不同帧目标的各种匹配中寻找最佳匹配，该过程可看作是一个分配问题求最优解的过程。随着目标数增加，计算复杂度增加，同时当目标被干扰和遮挡时，会出现匹配错误和跟踪丢失情况，因此当前研究主要集中在数据关联算法优化上。Zhong等人[3]针对目标位置和速度随时间变化具有非线性特征，采用粒子滤波通过近似非线性系统后验分布提高数据关联鲁棒性，但其准确性依赖于粒子数目，需要高昂的计算代价。Bewley等人[4]使用匈牙利算法，在跟踪预测目标和检测目标组成的二分图上逐帧求解最大匹配实现目标关联，但最大匹配不唯一，会导致匹配错误；为提高鲁棒性，Wu等人[5]引入相关滤波跟踪器，并采用分组关联：先将检测目标与具有较高滤波响应的跟踪目标利用匈牙利算法进行关联，再与低响应跟踪目标关联，算法计算量大；Liu等人[6]基于长短期记忆网络(Long Short-Term Memory, LSTM)模块中强记忆成分进行目标的分配预测，解决复杂情况下的漏检以提高关联准确度；为降低逐帧关联中误差累积造成轨迹漂移，Lenz等人[7]、Schulter等人[8]和Li等人[9]构建了最小代价流的数据关联框架，将相邻帧间目标相似性转化为网络流费用，通过最小费用流算法找到最优关联。作为多目标跟踪中的关键步骤，数据关联引起了广泛关注，但现有方法大都基于相邻帧的局部关联，一旦出现遮挡，会出现目标丢失或者ID转换。

为有效解决遮挡问题，很多方法采用两级关联方式，即考虑较短时间序列内目标较为稳定，依据目标检测结果，先在较短视频序列内对目标进行数据关联形成轨迹片段(tracklet)，再对轨迹片段进一步关联，最终形成目标完整轨迹[10]。相对于目标的完整轨迹，轨迹片段可以认为是目标的一段初级(low-lever)轨迹，即轨迹片段的生成可以认为是初级的数据关联。早期主要基于目标间的交并比(Intersection Over Union, IOU)[10-12]进行关联，但当目标间距离较近或出现遮挡时，IOU方法容易引起关联错误；Zamir等人[13]考虑相邻帧的同一目标具有相似的外观特征，提取目标外观信息生成轨迹片段，但外观特征依然对遮挡敏感；为此，Wen等人[14]在外观特征基础上联合运动信息关联目标生成轨迹片段，有效区分拥挤场景中具有相似外观的空间接近目标；Choi[15]基于光流信息提出聚合局部流描述符(Aggregate Local Flow Descriptor, ALFD)特征计算目标间的相似度生成轨迹片段，但ALFD的权重由目标之间的重叠度决定，易受遮挡影响；为克服不同目标距离接近时由于重叠导致的关联错误，Shen等人[16]利用目标IOU和最小成本流提高轨迹片段生成的准确性；Nahon等人[17]先利用IOU进行目标关联获得初始轨迹片段，当两个轨迹片段出现重叠时需进一步分割，该方法能够减少目标ID转换次数，但当目标长时间距离较近或遮挡时跟踪准确性下降；Wu等人[18]构建基于点云的轨迹片段生成卷积神经网络(Point Cloud based Tracklet Convolutional Neural Network, PC-TCNN)，利用连续帧中目标时空一致性特征生成轨迹片段。Dai等人[19]联合外观、时间和位置信息计算相邻帧目标的相似度，使用匈牙利算法生成轨迹片段。可以看出，现有轨迹片段生成方法也主要通过有限时域内相邻目标间的相似度匹配实现。

关联的准确性直接影响跟踪的准确性。现有方法主要基于时空一致性，根据最大匹配度(或最小匹配距离)进行关联，即根据时间顺序在相邻帧选择匹配度最大的目标进行关联。但最大匹配未必为准确匹配，一旦发生相似目标接近或者遮挡时，会产生错误关联，造成跟踪中断产生碎片跟踪，或直接导致跟踪失败。为清楚说明，图1显示了目标a和b的运动轨迹。其中，目标a在第k帧出现，第k+1～第k+4帧被遮挡，第k+5和第k+6帧重新可见，实心点1,7和8分别表示a在第k帧、第k+5～第k+6帧出现的位置，红色虚线表示a的轨迹；目标b在第k+1～第k+5帧出现的位置由实心点2～6表示，目标b轨迹如红色实线所示。实心点颜色代表目标的特征属性，颜色相似度表明归属于同一目标的可能性。现有方法主要关注相邻帧目标的成对相似性，因此尽管实心点1和2分属不同目标，但出现在相邻帧，又具有较高的相似性，故1和2关联后产生了错误的轨迹，如蓝色实线所示。当目标a在第k+5帧重新出现时，则作为新目标进行标记和跟踪，形成碎片轨迹，如黑色实线所示。

图1 局部和全局数据关联说明

因此，遮挡情况下，现有局部关联方法很容易造成目标丢失和目标ID转换。为实现鲁棒跟踪，本文提出基于次模优化的轨迹片段生成方法。首先，将目标关联转化为运筹学中的设施选址问题(Facility Location Problem, FLP)；其次，采用互补特征，并融合运动信息提高目标匹配准确度；最后，引入次模理论，根据次模函数性质，通过具有约束的次模最大化算法在视频片段全局内选择目标实现数据关联。具有约束的次模最大化算法在有近似保证的前提下可以达到近似最优的性能，因而所提算法可以有效提高跟踪准确性。同时，通过全局间的关联可以应对各种干扰和遮挡情况，提高跟踪鲁棒性。

2 设施选址及次模函数

设施选址问题是运筹学中优化组合领域一类重要的问题，在确定选址对象、选址目标数、成本函数以及存在的约束条件前提下，以总成本最低或总服务最优或社会效益最大化为总目标确定设施数量、位置等。设施选址问题模型为

其中，i∈C，代表客户集合C中任意客户，j∈F，代表设施集合F中为客户提供服务的设施；每个设施j对应一个非负的开放费用fj；设施j为客户i服务产生的利润为cij；xij表示设施j是否为客户i提供服务，根据约束条件式(5)，xij∈{0,1}，xij=1表示设施j为客户i提供服务，否则xij=0；yj∈{0,1}，yj=1表示开放设施j，否则yj=0； z为目标函数，表示获得的总收益；q为开设的最大设施数量。设置选址问题是在有限设施集合中选择开放哪些设施使得开启这些设施的成本费用和对客户服务产生的利润总和达到最大[20,21]。约束条件式(2)：保证每个客户都能被服务；约束条件式(3)：xij≤ yj保证只有开放的设施才能为客户提供服务。约束条件式(4)将最多开放的设施数量限制为q。设施选址问题可以看作是在设施集合中选择一个最优子集，将客户分配到每个设施，使设施开放成本和为客户服务获得的利润总和最大。设施选址问题是一个经典的NP-难问题，近似算法是解决NP-难问题的重要方法之一。很多学者已经证明设施选址问题中总利润函数，即式(1)满足次模性[22,23]，利用次模最大化可以获得近似解。

次模性(submodularity)又称子模性、亚模性等，是集合函数的一个属性。对于有限集合V，A⊆B⊆V，元素a∈V B，对于集合函数H: 2V→R，如果满足

则函数H满足次模性，具有边际效益递减(diminishing returns)性质[24]。

根据次模函数性质[25]，当函数满足次模性和单调性，且在定义域上值域非负时，与最优解相比，使用贪婪算法可获得至少(1-1/e)≈63%的近似解。文献[26]通过在各种大规模现实世界数据集和实例上进一步证明贪婪算法得到的近似解其近似比α(Approximation Ratio, AR)几乎总是超过85%，并且经常超过95%，即近似解Sapp相对于最优解Sopt满足：α·Sopt≤ Sapp≤Sopt。因此，有效解决了设施选址这类NP-难问题并可达到近似最优的性能。

3 次模优化的轨迹片段生成

本文将视频片段第1帧检测目标作为初始目标，视为设施选址问题中的客户集合；其余帧的检测目标作为候选集合，视为设施选址问题中设施集合。初始目标与其余帧检测目标之间的相似度作为设施满足客户需求所获得利润，轨迹片段的生成可以看作对每个初始目标(客户)，在候选集合(设施集合)中选择与初始目标相似的目标，即选择设施以满足客户需求获得最大利润。因此，轨迹片段生成问题转化为设施选址问题，即为每个初始目标在候选集合中根据相似性选择最优子集，该问题可以通过次模最大化函数来解决[22,23]。因此本文利用次模优化实现目标关联生成轨迹片段，一方面利用次模函数性质，使用贪婪算法得到接近最优解的近似解，保证关联准确度，另一方面，突破时域相邻目标间的局部关联限制，在候选集合全局范围内实现目标关联，有效解决遮挡问题。

3.1 轨迹片段生成问题转化

将视频V分割成L个视频片段，即V={V1,V2, ···, Vi, ···, VL}，每个视频片段帧数为K。以第m个视频片段为例，构造图G=(Dm, Em)说明轨迹片段的生成过程，如图2所示，Dm为第m个视频片段检测出的目标集合，目标间连线e∈Em代表目标间的关系，本文选择目标相似度进行关系度量，同一帧目标间不进行关联，则Dm表示为

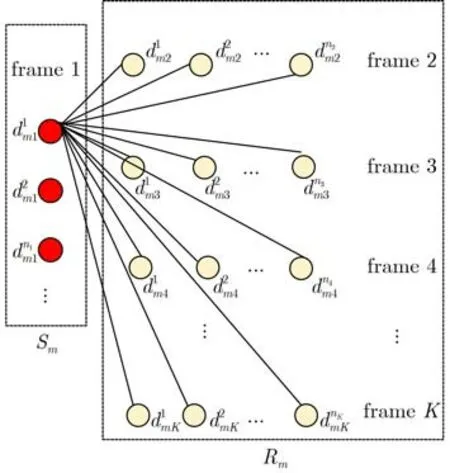
图2 轨迹片段生成过程示意图

轨迹片段生成就是根据初始目标在候选集合选择相似度最优子集，即将Rm根据与初始目标相似度划分为不同子集。以相似度作为设施满足客户需求所获得的利润，轨迹片段生成问题转化为设施选址问题，根据式(1)-式(6)，本文将设施选址问题应用于轨迹片段生成

其中，Rm目标总数为N； xij∈{0,1}，若Rm中所选目标j属于初始目标i的轨迹片段，xij=1，否则xij=0；sij是初始目标i与候选集合中目标j之间的相似性；开放设施j的成本ϕj设为固定值γ，本文γ=0。约束条件式(10) 保证视频片段中所有目标都能被分配到对应轨迹片段中，即属于某个子集；约束条件式(11)保证每个轨迹片段长度不长于视频帧数K，即保证至多有K个检测目标组成一个轨迹片段；约束条件式(12)保证每个视频帧最多只有1个检测目标被选入当前轨迹片段，即同一帧中不可能有两个目标同属一个轨迹片段。利润函数z满足次模性[22,23]。

3.2 目标特征提取

根据式(9)进行目标关联，首先要计算目标相似度。跟踪过程中目标姿态、尺度，环境光照等会发生变化，单一特征表征目标能力有限。本文通过实验发现方向梯度直方图(Histogram of Oriented Gradient, HOG)与颜色名(Color Name, CN)特征具有很好的互补性：HOG对光照变化鲁棒，但对目标形变敏感，颜色特征易受光照影响，但在目标形变下较为稳定。因此本文选取CN和HOG特征进行目标表征。

颜色、形状相似目标间会产生互相干扰，如图3(a1)TUD-Stadtmitte数据集第50帧目标4与图3(a2)第52帧目标匹配时，与第52帧最左边目标(实际对应第50帧目标6)相似度(0.972)高于与第52帧最右边目标(实际对应第50帧目标4)相似度(0.968)，使第50帧目标4与第52帧最左边目标发生错误关联。考虑目标在视频片段(本文设为10帧)所属时间内运动范围有限，若两个目标距离较远，分属不同目标的可能性较大，因此本文利用运动信息，改造Sigmoid函数设计权重系数λ提高匹配准确度，λ随着目标间距离增大而降低，示意图如图4，则目标相似性度量sij表示为

图3 权重系数λ加入前后跟踪结果对比

图4 相似度权重系数λ

其中，w为每个初始目标检测框宽度，由检测算法给出；x代表两个目标间距离，通过计算目标检测框中心距离获得；分别代表初始目标集第i个目标和候选目标集第n帧第j个目标的CN和HOG特征相似度。图3(b1)和图3(b2)显示了加入权重系数后可以有效避免相似目标干扰下的错误关联。

3.3 次模最大化

本文将轨迹片段生成问题转化为设施选址问题，设施选址问题是一个NP-难问题，但满足次模性。根据第2节所述，采用贪婪算法可以有效解决设施选址这类NP-难问题并能获得接近最优解的近似解。因此本文利用次模优化将轨迹片段生成过程进一步转化为

其中，sij是初始目标(客户)i与候选集合中目标j(设施)之间的相似性，开放设施j的成本ϕj为固定值γ，本文γ=0。NA代表选择候选目标的最大数量(开放设施的最大数量)，K是视频片段帧数，N是全部候选目标数量。根据次模函数性质，采用贪婪算法，对每一个初始目标，在候选目标集合中选择与其具有最大相似度的目标构成子集A，该子集中的目标组成对应初始目标的轨迹片段。

为清楚描述利用次模优化生成轨迹片段的过程，选取TUD-Stadtmitte数据集第17～32帧含遮挡情况的视频片段进行说明，如图5所示。提取视频片段第1帧目标作为初始目标集Sm，其余视频帧目标组成候选目标集Rm，红色实心点代表Rm中各个目标。根据式(14)计算每个初始目标与候选目标的相似度，选取相似度最大的目标。以17帧初始目标集第2个目标为例，与其相似度最大的是第18帧目标2，故首先选取，此时根据约束条件式(12)，即1个轨迹片段在同一帧中最多选取1个目标，故将第18帧其他目标从Rm剔出，后续只在19～32帧中选择；第2次计算发现与第19帧目标2相似度最大，则选择归入当前轨迹片段中，同理将第19帧其他目标从Rm剔出。以此类推，后续依次选择第32帧目标2，第20帧目标2。由于遮挡，初始目标2与第22～31帧任意目标相似度均小于阈值α，故在第22～31帧没有获得匹配目标，获得的匹配对象是，图5中带阴影红色点所示。最后依据目标所在帧的时间序列获得初始目标的轨迹片段为。现有方法在目标遮挡后受局部相邻帧关联的限制，在第32帧目标再出现时可能会作为新目标分配新的ID。为此很多方法，例如DeepSORT[27]需要设定额外的步骤和参数处理遮挡问题。本文方法则基于次模理论通过候选目标集中的全局关联直接克服遮挡问题。

上述过程说明了视频片段中一个初始目标的轨迹片段生成，从候选目标集合中删除该轨迹片段所包含目标，再对其他初始目标依次做相应处理获得对应轨迹片段。值得注意的是，视频片段初始目标集合匹配完成后，候选集合中可能还有未匹配目标，代表视频片段中间帧新出现的目标，此时以这些新目标作为初始目标依次进行匹配关联。最终生成视频片段Vm的轨迹片段集合Tm={,,...}，其中表示第m个视频片段Vm中的第j个轨迹片段。整个过程如算法1所示。

4 实验结果与分析

为验证本文算法的跟踪效果，首先在多个公开数据集上与常用轨迹片段生成算法进行定性比较，然后基于多目标跟踪挑战赛(Multiple Object Tracking Challenge, MOT Challenge)评价指标[28]进行定量评估。

4.1 实验数据集

本文选取公开数据集MOT17,PETS09-S2L1和TUD进行实验。 MOT17由7个训练集和7个测试集组成，包含夜间、高密度行人、快速运动场景图像序列，每个序列分别使用尺度相关池化(Scale Dependent Pool, SDP)、可变形组件模型(Deformable Part Model, DPM)和快速区域卷积神经网络(Faster Region-based CNN, Faster-RCNN)获得目标检测结果；PETS09是行人交通数据集，包括不同场景下S0,S1,S2,S3 4个子集，本文选用常用于行人跟踪的PETS09-S2L1进行实验；TUD主要用于拥挤场景下的行人多目标检测和跟踪，其中TUDStadtmitte和TUD-Crossing是低视角下拍摄的繁忙步行街场景，包括频繁的遮挡情况。

4.2 定性评估

为验证算法在遮挡情况下的跟踪效果，在上述3个基准数据集分别选择含遮挡情况的3个视频序列进行实验。最小代价流是目前轨迹片段生成的常用方法，与本文方法的对比实验结果如图6-图8所示。最小代价流方法在遮挡情况下出现了目标ID转换和丢失情况：图6(a2) MOT17数据集第6帧目标13丢失；图7(a1) TUD-Crossing数据集第40帧目标4被遮挡后在图7(a3)所示第50帧重新出现后被认定为新目标12，发生目标ID转换；图8(a1) PETS09-S2L1数据集第51帧目标2在图8(a2)所示第54帧被遮挡，图8(a3)第61帧重新出现后被认定为新目标8，目标ID发生转换。相比较，本文方法在上述情况下保持目标ID 不变，实现鲁棒跟踪。

算法1 基于次模优化的轨迹片段生成

图6 MOT17-02数据集实验结果对比

图7 TUD-Crossing数据集实验结果对比

图8 PETS09-S2L1数据集实验结果对比

4.3 定量评估

轨迹片段作为初级轨迹，直接关系到多目标跟踪完整轨迹的准确性。本文将轨迹片段进一步关联成完整轨迹，利用MOT Challange跟踪评价指标对算法性能进行定量评估。其中包括算法跟踪准确性(Multiple Object Tracking Accuracy, MOTA)的评价；算法的关联性能IDF1综合考虑目标ID的准确率和召回率；算法跟踪精度(Multiple Object Tracking Precision, MOTP)评估；跟踪目标ID转换次数(IDentity Switches, IDS)计算；跟踪过程中各目标至少有 80%的视频帧能被正确跟踪的轨迹占总轨迹的占比(Mostly Tracked, MT)统计；丢失轨迹的占比(Mostly Lost, ML)统计，其中丢失轨迹为至多有 20%的视频帧能被正确跟踪的轨迹。

表1和表2显示了不同数据集上的算法跟踪性能比较结果。其中↑表示数据越高越好，↓表示数据越小越好。跟踪结果与检测器精度直接相关，为公平比较，本文与参与比较的近年来主要的MOT算法全部采用数据集提供的检测结果进行跟踪性能比较，各个算法的实验数据由相关文献提供。表1 PETS09-S2L1和TUD数据集上，目标主要为行人，外观相似，存在频繁遮挡，对跟踪器的鲁棒性提出了很大的挑战，结果显示本文方法均产生最高的MOTA和最低的IDS，说明本文方法可以很好地解决目标遮挡导致的ID转换问题，实现鲁棒跟踪。在表2 MOT17数据集中本文方法在MOTA和IDF1两个指标上超越了大多数方法，其中两项指标上表现较好的方法都是采用卷积网络跟踪模型，需要优化调整模型参数，与这些方法相比，本文算法对参数依赖性小，计算简单。在上述基准数据集上本文方法IDS指标最低或接近最低，实现了较低的目标ID转换次数，同时有更多的物体被准确追踪(高MT和低ML)。

表1 PETS09-S2L1和TUD数据集跟踪性能对比

表2 MOT17数据集跟踪性能对比

5 结 论

本文采用两级关联方式，通过生成轨迹片段构建目标的完整轨迹实现多目标跟踪，提出次模优化框架下轨迹片段生成方法，在全局范围内利用次模最大化选择最优子集生成轨迹片段。在MOT17,PETS09-S2L1和TUD基准数据集上的定性和定量实验中，本文方法表现出较好的对干扰和遮挡的处理能力，同时与现有方法相比，也取得了具有竞争力的跟踪性能。