欠采样下的多频带通信信号高精度载频估计

黄翔东 宋金水 李燕平

(天津大学 天津 300072)

1 引言

非合作目标的载频估计是通信侦察中的关键环节，旨在从宽范围监测频带中快速、高精度地捕获目标频率位置。其接收机通常采用超外差结构，即将射频信号与本振信号相混频，并借助中频滤波器提取出其固定频带，再进行模数转换与数字谱分析；然而该方法因依赖混频器、本振和中频滤波器等模拟器件(当进行大范围载频捕获时，甚至需要设置多级混频)，存在硬件成本高、功耗大、不易小型化的缺点[1-3]。为克服该缺陷，将数字采样从中频段前移至射频段是载频估计的趋势。然而，若在射频端直接采用经典奈奎斯特采样模式，需使用高速模数转换器(Analog-to-Digital Converter,ADC)，这对系统的硬件成本和功耗都提出很高要求。因而，欠采样下的非合作目标的载频估计是当前频谱分析迫切需要解决的问题，而欠采样下的频率估计难点在于解决混叠频率的解模糊问题。

为解决混叠频率的解模糊问题，常用方法有以下3种。(1)利用中国余数定理(Chinese Remainder Theorem, CRT)完成折叠整数的计算[4,5]，然而直接用这些CRT算法处理具体欠采样波形时，只能适用于复数信号，不能适应于实数信号，其原因是CRT必须依赖多路欠采样，即使对于单频信号，其单通道实数波形必然对应两个复指数谱边带，从而m ≥2路多通道采样就会产生2m个余数，故必然对仅需m个余数的CRT重构造成余数选取模糊问题。(2)借助多通道互素欠采样，利用查找表或频率配准完成混叠频率的解模糊[6,7]。这种方法依赖多通道欠采样率的互素关系，频率检测范围受限于多通道欠采样率的最小公倍数，不适用于在大带宽频率检测范围内对非协作信号的频率估计。(3)借助欠采样谱分析方法估计出全景谱避免欠采样导致的频率混叠问题，再利用其他手段完成频率校正。目前主流的方法为借助基于调制宽带转化器(Modulated Wideband Converter, MWC)的谱分析方法估计出信源在整个频率检测范围的频谱支撑，再通过将每个频谱切片移动到频谱中的适当位置并叠加生成奈奎斯特采样序列，进而完成频率估计[8-10]。显然，基于MWC的谱分析并恢复奈奎斯特采样序列完成载频估计的关键点在于正确估计出信源的频谱支撑。

具体来说，基于MWC的频率估计方法采用多路并行欠采样结构，在每路ADC前用乘法器、高频脉冲发生器和模拟低通滤波器替代了超外差的混频器、本振和中频滤波器，故其模拟电路成本和功耗有所降低；在谱重构算法设计方面，MWC通常采用压缩感知重构算法以构造全景谱。近年来，该方法被用于非合作目标的联合到达角和载频的估计方法中[11-13]。

然而MWC方法仍存在欠采样通道数目多、载频估计精度低和对信源频带分布稀疏度约束条件高等缺陷。原因在于：(1) MWC的谱重构方法是基于压缩感知原理的，要求欠采样通道数目m ＞2U，U为谱成分数目；(2) 压缩感知谱重构算法只能将载频定位在有限的谱支撑区上，奈奎斯特序列的生成只是简单的频谱切片合并，其频率估计精度受限于频谱支撑的准确性；(3) 压缩感知重构条件要求信源稀疏分布，当多信源呈现密集分布时(如信源跨越多个谱支撑区情况)，MWC方法即失效。因此，目前MWC方法的最新研究进展都在于提高频谱支撑估计的准确性。文献[9]通过判断2次重构的子带能量之间的相关性判断MWC压缩采样重构是否准确。文献[10]改进了谱重构中使用的贪心算法(即最短距离正交匹配跟踪算法)，不仅将谱重构的复杂度降低50%，而且具有更好的谱支撑集估计精度。

为根本解决当前主流的MWC欠采样谱分析方法的3个问题，本文提出基于互素谱相位差校正的通信信号载频估计方法，该方法只需在两路互素欠采样条件[14,15]下，即可实现包含多个通信信号的高精度载频估计，且适合于跨频段和密集谱估计。

2 互素欠采样概述及问题分析

经典互素谱分析流程如图1所示。

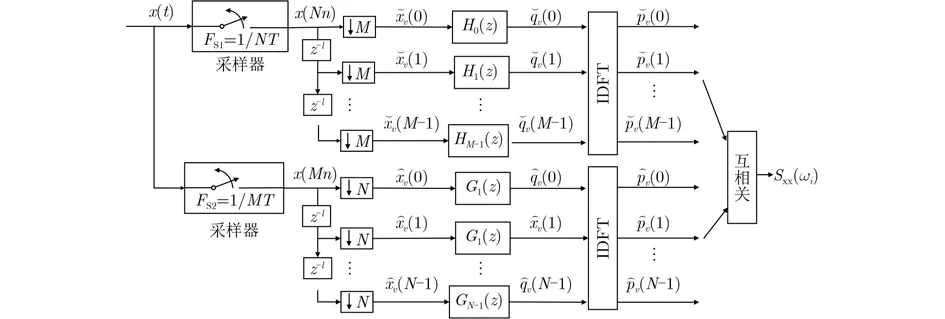
图1 经典互素谱分析流程图

图1中，M, N为互素整数对, 设定载频估计上限频率为FN(对应Nyquist采样周期T=1/FN，快拍周期为MNT)，则两路互素欠采样速率设置为FS1=FN/N,FS2=FN/M。图1中子滤波器Hk(z),Gl(z) 是由截止频率为 π/M, π/N的原型低通滤波器H(z),G(z)做多相分解而得[14,15]

从图1可看出，两路欠采样序列x(Nn),x(Mn)分别经过多相滤波(上、下通道的支路滤波器分别为H0(z),...,HM-1(z),G0(z),...,GN-1(z)), IDFT运算和通道间各支路的互相关扫描，即得互素谱输出Sxx(ωi),i=0,1,...,MN-1 其 中ωi=iΔω,Δω=2π/MN。

然而，作为离散谱分析方式，互素谱的频率分辨率受限于 Δω=2π/MN[15](对应的模拟频率分辨率为 Δf=FN/MN)，该分辨率仍无法满足实际载波频率估计精度要求。为提升精度，一方面需挖掘载频与互素谱通道的映射关系，基于此设计互素谱校正方法，实现高精度载频估计；另一方面需设计提升互素谱分析的分辨率的措施。

3 载频估计方法

3.1 载频与互素谱通道映射关系分析

以单频带二进制相移键控调制(Binary Phase Shift Keying, 2PSK)信号为例说明该映射关系，2PSK信号为

其中，载频fc=(i+δ)Δf,fc＜FN/2 ,Δf=FN/MN, i是载频的整数部分 (0≤i ≤MN/2-1),δ是载频的小数部分 (-0.5≤δ ＜0.5)。a[u]是2PSK调制符号序列，TB为符号周期，g(t)是脉宽为TB的脉冲整形函数。

显然，x(t) 的 Nyquist样本为(为方便，将s(nT)表示为s(n))

则在采样率为FS1的上通道中，第个时延器的输出为

进而对x(N(n-))做抽取因子为M的下采样后，其各路子滤波器实际工作在FS1/M的低速率上，由于MN个Nyquist样本组成1个快拍，则对于第v个快拍，子滤波器(z)的输入信号可等价表示为

考虑到欠采样可能会使得式(7)中的角频率(i+δ)2π/M超过 2π，因此该角频率可表示为

同理，在下通道中，角频率(m+δ)2π/N也可表示为

其中“ [·]”为四舍五入取整。联立式(10)、式(11)，则可推导出如下数字载频值fc/Δf与互素谱IDFT输出支路序号对(k, l)、频偏之间的映射关系

其中，fc/Δf实际为 (i+δ)，故从式(13)中可推出，两个待定折叠整数可通过对全景谱序号i作如式(14)的模除下取整操作而确定，即

因而，精确载频估计的关键在于：(1)准确获知谱序号i(即要求产生无伪峰全景谱)；(2)精确估计出频偏值δ(可通过本文提出的相位差校正方法求得)。

3.2 两路并行互素谱分析

本文设计出如图2所示的两路并行互素谱分析器，不仅可消除经典互素谱分析的伪峰效应[16]，而且还可将频率分辨率提升1倍。

图2 两路并行互素谱分析器

图2中H(1)(z),G(1)(z),H(2)(z),G(2)(z)为本文设计的最小尺寸全相位滤波器，使用其作为互素谱分析中的原型滤波器可以降低载频估计方法的计算复杂度。该设计要求对理想原型滤波器频率响应H(jω),G(jω)做最小尺寸采样，可得如式(15)的两个最短频率采样向量

为构造两路并行互素谱分析，不妨对向量H,G作如式(16)的对半分解

进而采用文献[17]的基于偶对称频率采样的全相位滤波器设计法，可推导出与这4个频率向量相对应的H(1)(z),G(1)(z),H(2)(z),G(2)(z)对应的原型滤波器系数分别为

其中，wc(n)为 单窗卷积窗函数[17]，将H(1)(z),G(1)(z)进行多相分解所得的子滤波器代入图2的第1路互素谱分析，将H(2)(z),G(2)(z)进行多相分解所得的子滤波器代入其第2路互素谱分析，则可分别在如下两个频点集合Γ1,Γ2中得到各自的功率谱估计结果

进而将Γ1,Γ2的两路谱分析结果合并，即可得全景谱Sxx(ω),ω ∈Γ1∪Γ2。既然Sxx(ω)的观测频点数相比于经典互素谱分析增加了1倍，其频率分辨率也相应提升1倍。需指出的是，源于最小尺寸全相位滤波器对半分解的作用，全景谱Sxx(ω)可根本消除经典互素谱分析的伪峰效应，保证了可从互素谱输出中准确取得式(14)所需的全景谱序号i。

令M=23, N=19,FN=6.555 GHz，则Δf=FN/MN=15 MHz ，对频率为 130.48Δf、幅值为2、初始相位为 3π/7的余弦信号进行欠采样谱分析。图3(a)、图3(b)分别给出了经典互素谱分析和本文提出的两路并行互素谱分析的全景谱估计结果(由于为实信号，只给出了左半频率轴)。

图3 经典互素谱分析、两路并行互素谱分析的全景谱

从图3(a)可看出，除期望位置i=130处，经典互素谱分析还产生了3根冗余伪峰；而图3(b)本文提出的分析器则完全消除了伪峰效应，仅从谱峰位置即可确认全景谱序号i。

3.3 基于相位差的互素谱校正方法

本文提出基于相位差的互素谱校正方法用于估计式(13)中的频偏值δ，以提升载频估计精度。将从全景谱观察到的频率fc的序号i、频率f的序号i*分别代入式(12)，可分别得到与fc对应的余数对(k,l) 和与对应的 (k*,l*)。

注意到图1的互素谱分析过程只涉及移相、滤波、加法和IDFT等线性运算，从而整体上可将其视为线性系统。故可基于线性性质，推导相邻快拍激励下的IDFT输出(k)与v+1(k)之间的相位关系。

不妨将式(3)的当前第v个快拍的激励表达为

式(19)的基带信号s(n)实际表征通信载频包络，当符号率不高时，其相邻快拍采样值可视为不变，即s(n+MN)≈s(n) ，基于此，可推出第v+1个快拍的激励表达式为

联立式(19)、式(20)可发现:对于ωc成分，相邻快拍之间的激励变化可完全由复增益ejωcMN来表述，从而根据线性系统的齐次性，上通道的第v个快拍和第v+1 个快拍的IDFT输出值(k),v+1(k)存在如式(21)的简单相位关系

式(22)中未知整数m*引起的整周模糊度可通过如下模除求余操作而消除

既然δ ∈[-0.5,0.5)，进而可推导出上通道第v个快拍第k路IDFT输出的频偏估计

类似地，也可获得下通道第v个快拍第l路IDFT输出的频偏估计值。并在L个快拍范围内对,作平均，即可得到更高精度的频偏估计

进而结合两路并行互素谱分析器观测到的全景谱序号i,可得到如式(26)的载频估计值

3.4 算法流程总结

容易将以上过程推广至多频带通信信号情况，其载频估计流程可总结为算法1所示。

4 实验验证

4.1 多频带数字已调信号的载频估计

算法 1 多频带通信信号载频估计流程

设互素整数对M=23, N=19，上限Nyquist频率FN=6.555 GHz， 两路欠采样率分别为FS1=FN/N=345 MHz,FS2=FN/M=285 MHz，原始频率分辨率Δf=FN/MN=15 MHz。结合式(17)设计出最小尺寸全相位滤波器，构造出两路并行互素谱分析器，其频率分辨率为 Δf/2=7.5 MHz。测试信号为如式(27)所示各自包含U=4个频带的幅移键控(Amplitude Shift Keying, ASK), 正交相移键控(Quadrature Phase Shift Keying, QPSK)信号

其中，sASK(t),sQPSK(t)分别为对应基带信号，载频f1,f2,f3,f4依次为： 28.12Δf,29.88Δf,42.11Δf,86.96Δf，相应的通信信号带宽分别为0.5Δf, 0.5Δf,1Δf, 3Δf,z(t)是加性高斯白噪声。向并行互素谱分析器馈入时长为100个快拍的欠采样样点(对应上通道馈入100M=2 300个样点x1(n)，下通道馈入100N=1 900个样点x2(n))。图4给出信噪比SNR=10 dB时，两路并行互素谱分析器对QPSK信号估计的全景谱。

图4 两路并行互素谱分析的全景谱

定性而言，从图4全景谱分布，可发现其呈现如下特征:

(1)共包含4簇谱线，与真实源数目一致，证实了所提出的两路并行互素谱分析器可根本消除伪峰；

(2)不仅能识别带宽不超过 Δf的窄带成分(如f1,f2,f3)，而且可识别超过 Δf的宽带成分(如带宽为3 Δf的f4成分)。

(3)可以区分间距仅为1.76 Δf的密集谱成分f1,f2。

定量而言，在 SNR∈[-18 dB,10 dB]内改变信噪比对本文方法做测试，分别估计包含4个频带的ASK信号、QPSK信号的载频，对每种SNR和每种数字调制情况，开展D=1 000次蒙特卡洛试验，每次试验按式(28)算出其相对误差ξd进而取所有试验结果的数学期望，即可得总体相对误差ξ=E(ξd)。 对于QPSK和ASK两种数字调制情况，其载频估计的相对误差总体测试曲线如图5所示。

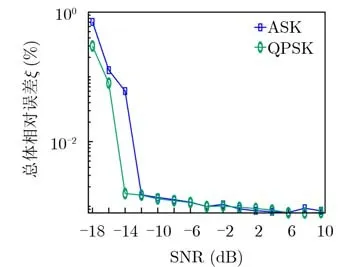
图5 本文方法载频估计的相对误差曲线

结合图5与信源分布，可得以下两点结论：

(1) 当信噪比高于-10 dB时，两种数字调制的载频估计相对误差均低于0.002%。

(2) 由于信源分布包含密集频带和大带宽成分，反映出本文方法对信源稀疏性不作限制。

4.2 与基于压缩感知的载频估计方法比较

为检验本文方法的载频估计精度，将其与基于MWC欠采样结构的压缩感知估计方法对比，文献[10]报道了该方法的最新研究进展(对支撑区重构算法的改进)。本文方法的参数设置沿用4.1节不变。而在MWC方法中，设定其欠采样通道数为m=40(其检测频带数目理论上限为20)，欠采样因子B=195，单通道欠采样率为FS=FN/B=33.6 MHz，MWC中的调制脉冲周期Tp=1/FS=29.76 ns，在谱重构阶段，使用文献[10]所提出的最短距离正交匹配跟踪算法完成信源频谱支撑的估计。测试信号选为，在 SNR∈[-20 dB,10 dB]内，频带数量在U ∈[2,16]内 变化的QPSK信号(符号周期同为 0.267 μs，对应信号带宽同为 0.5Δf)，U个载频均在(0,FN/2)随机生成。图6给出两种方法的相对误差曲线。

图6 两种载频估计方法的相对误差曲线

结合图6和两种方法参数设置，本文所提出的载频估计方法具有如下优势：

(1) 本文方法具有远比MWC方法更高的载频估计精度。 表现在，当U=2, 4时， MWC载频估计方法(虚线)相对误差低于0.01%的SNR阈值分别为-14 dB, -12 dB；而本文方法(实线)的相对误差在SNR∈[-20 dB,10 dB]范围内始终低于0.01%，且在SNR大于-12 dB时，相对误差甚至低于0.001%。

(2) 本文方法具有远比MWC方法更高的稀疏度鲁棒性。表现在，当成分数量U=8时，MWC方法的SNR门限为 -4 dB, 而本文方法SNR门限则为-12 dB，在SNR=10 dB时，本文方法的相对误差为MWC方法的1/20；当成分数量U=16时，已无法绘制出MWC的相对误差曲线，而本文方法SNR门限则为 -10 dB。这是因为：一方面，MWC的压缩感知重构失败概率随信噪比降低会急剧增大；另一方面，当随机成分数量U增大时，产生密集信源分布的可能性增大，使得待估计信源分布不满足压缩感知对信源稀疏度的要求，导致谱重构失败。而本文方法对以上两个因素不敏感。

(3) 本文方法具有远比MWC方法更高的样本利用率。表现在，MWC方法所需的总采样率为mFS=1344 MHz ，而本文所需的总采样率为FS1+FS2=630 MHz，由于两者观测时段相同，意味着本文方法消耗的样本数仅为MWC方法的630/1344=46.88%，即获得如上所述的载频估计性能的全面改善效果。

5 结论

本文提出互素欠采样条件下的多频带通信信号高精度载频估计，通过将两路并行互素谱分析与基于相位差的互素谱校正方法结合起来，既克服了MWC欠采样结构的载频估计方法存在的欠采样通道多、精度低、稀疏性要求等不足，又弥补了经典互素谱分析存在伪峰效应的缺陷，且突破了频率分辨率限制，提高了载频估计的精度。故在通信侦察、电子支援等非合作目标载频捕获中具有广阔的应用前景。