Experimental study on the size effect on the equation of state of concretes under shock loading

Mei Li , Jian Cui , Yanchao Shi , Baijian Tang , Xin Chen

a Key Laboratory of Coast Civil Structural Safety of the Ministry of Education, Tianjin University, Tianjin 300072, China

b School of Civil Engineering, Suzhou University of Science and Technology,1701 Binhe Road, Suzhou 215011, Jiangsu, China

c School of Civil Engineering, Tianjin University, Tianjin 300072, China

Keywords:Concrete Equation of state Size effect Shock wave Fly-plate impact test

ABSTRACT Adopting the classical theory of hydrocodes, the constitutive relations of concretes are separated into an equation of state (EoS) which describes the volumetric behavior of concrete material and a strength model which depicts the shear properties of concrete.The experiments on the EoS of concrete is always challenging due to the technical difficulties and equipment limitations, especially for the specimen size effect on the EoS.Although some researchers investigate the shock properties of concretes by fly-plate impact tests, the specimens used in their tests are usually in one size.In this paper, the fly-plate impact tests on concrete specimens with different sizes are performed to investigate the size effect on the shock properties of concrete materials.The mechanical background of the size effect on the shock properties are revealed, which is related to the lateral rarefaction effect and the deviatoric stress produced in the specimen.According to the tests results,the modified EoS considering the size effect on the shock properties of concrete are proposed, which the bulk modulus of concrete is unpredicted by up to 20% if size effects are not accounted for.

1.Introduction

Concrete materials are widely used in military and civilian constructions.In their service life, the structures might subject to multi-hazard loads such as explosion, impact or other high dynamic loads.The high dynamic loads like close-in explosion can produce high pressures in gigapascal region within microseconds which can cause remarkable shock waves in the affected solid body.While Finite Element (FE) codes are typically used for static problems,hydrocodes are required for highly dynamic problems such as shock and impact[1,2].Within hydrocodes,the stresses and strains are divided into hydrostatic and deviatoric portions.An equation of state(EoS) is used to describe the volumetric behavior of concrete material and a strength model is related to the deviatoric material behavior[3-5].To study the strength model of the concretes under dynamic loading, some comparatively simple tests such as SHPB tests are used [6-10].However, for the study of EoS of concrete materials, the tests become challenging and expensive i.e., either the fly-plate impact tests[11-15]or the full-scale detonation tests[16-18] are needed.In these tests, the loading process is usually adiabatic and the strain rates of the material could reach about 104～108s-1[19,20].For the explosion experiments, the very high pressure and super high dynamic material properties should be recorded near the detonation charge which have extremely measurements difficulties.On the other hand, the explosion products influence the testing results a lot [2,16].Therefore, the fly-plate impact test become a more commonly used test method to study the shock characterization of solid materials [21-24].

Analysis of concrete shock behavior by fly-plate impact tests has been an active research field over the last decades.A number of researchers[16,20,25]have investigated shock-induced response of concrete ranging from low velocity up to strong shock loading as high as around 1000 m/s impact velocity and strain rates of 105s-1Grady[26]studies the shock compression and release of concrete in fly-plate impact tests by a single stage 89 mm diameter smoothbore powder gun.Gebbeken et al.[16] measured the longitudinal stress wave on disc-shaped concrete specimens with a diameter of 58 mm to characterize the shock response of the concrete material.Hall et al.[25] study the influence of aggregates on the concrete shock properties and they indicate that concrete does not exhibit a strong dependence upon aggregate size in the stress range of 3-25 GPa of their fly-plate impact tests.Some scholars[1,2,27]also study the shock-induced properties of concrete by means of both the numerical simulation and impact tests,and the diameters of the specimen used in their studies are from 40 mm to 80 mm respectively.Riedel et al.[20]also give an overview of available literature data from 13 article papers and find that the shock particle velocities of specimens with different sizes have a large scatter.

The results from the above mentioned shock wave studies,especially in Riedel et al.’s review,indicate the high discreteness of the concrete shock properties under fly-plate impact tests.The scattered results can be attributed to the following two reasons.On the one hand, concrete is a complex heterogeneous material containing mortar, aggregates,and interfacial transition zone[28-31]and the results from above researchers and summarized by Riedel[20] are from different experiments, affected intensively by the samples preparation process, the aging and curing conditions,and thus there is a lack of reproducibility between samples.On the other hand, the size of the specimen in the above mentioned studies are different and the maximum diameter of the specimen is only 89 mm due to the limitation of the bore of the gas gun.It is well known that in dynamic strength tests, the specimen size can influence the dynamic results due to the longitudinal inertia effect,lateral inertia effect and the dynamic fracture mode which are related to the complex stress wave propagation and reflection within the specimen under impact loads.Similarly,in the EoS tests,the lateral stress wave can reflect from the free surface of the specimen to reduce the intensity of the shock waves and the longitudinal unloading wave propagating within the specimen can also reduce the intensity of the shock wave,which make the results questionable.Therefore, the shock results can be affected by the diameter of the specimen and the slenderness ratio (ratio of the width to the thickness)of the concrete specimen may influence the propagation and reflection of the shock waves within the specimen significantly.However, from all above reviews, few researchers have conducted a systematic and detailed study on the size effect on the shock properties of concretes,thus,this paper carried out a series of fly-plate impact tests to complete and supplement the research in this area.Concrete specimens with diameters range from 50 mm to 150 mm were prepared to investigate the influence of specimen size on the shock properties of concrete by a gas gun with a super-large diameter of 152 mm developed in Tianjin University.The mechanical background of size effect on the shock properties of concretes will be revealed and the modified EoS considering the size effect on the shock properties of concrete are proposed to more accurately express the Hugoniot states of concretes.

2.Experimental procedures

2.1.Fly-plate impact theory

Under high dynamic loads, the material formulations can be described by the three classical theories of thermodynamics,namely, the conservation equation of mass, energy and momentum.These three conservation equations are usually described by the parameters of density ρ, particle velocity μ, hydrostatic pressure P and internal energy E[3,4].Another equation is needed to solve these four physical quantities in the three conservation equations,and the EoS is used as a supplementary equation to solve these four physical quantities.The EoS is usually used to describe the relationship between pressure P and density ρ [32,33].Fig.1 shows a classical pressure-density relation (P-ρ relation) of the porous material.As shown in Fig.1, for the porous material like concretes, the material with an initial density ρ0starts to deform plastically when a certain hydrostatic pressure, i.e., the Hugoniot-Elastic-Limit (PHEL) with the corresponding density ρcrush, is reached [1].During continuous compaction,the pores deform and collapse with a certain amount of energy absorption until the material is completely compacted and reaches the pressure at total compaction Pcomp.

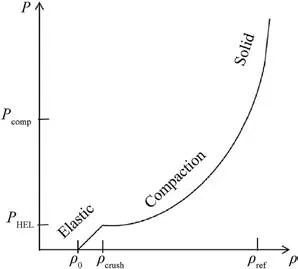
Fig.1.P-ρ relation of porous material [1].

The conservation of mass,energy and momentum which can be expressed as follows [16,34,35],

where the subscripts 0 and 1 refer to the states of unshocked and shocked material.ρ, μ, P, E describe the density, particle velocity,pressure and internal energy respectively,D is the shock velocity.In the tests,the initial parameters of the state of unshocked material,namely ρ0, μ0, P0, E0, is known.E0corresponds to the actual temperature.The atmospheric pressure P0is very small compared with P1,thus is usually neglected.In Eq.(2),if μ0is equal to 0 at the initial time,

in the above equations, there are four parameters P1, E1, ρ1and μ1are unknown and therefore EoS shown in Fig.1 is another supplementary equation to determine all parameters.For material dynamic analysis,an another form of EoS,namely the D-μ relation(Hugoniot EoS) delivers an adequate description of the volumetric material behavior [1,36,37].For most of materials, this Hugoniot EoS can be expressed in a linear relation [1,2,36],

where the constant S and C can be determined by the tests and C is also called bulk wave speed.Based on Eq.(5)and the conservation equation of mass and momentum, the classic Mie-Grueneisen equation of state which describes the shock state of solid materials in P-ρ relation can be obtained as follows,

in this paper, the relationships between shock velocity D and particle velocity μ of different sizes specimens are investigated in the tests firstly and then the P-ρ relations can be obtained by Eqs.(6)and (7).In this way, the size effect on the shock properties of concrete in fly-plate impact experiments can be studied comprehensively.

2.2.Fly-plate impact testing system

The fly-plate impact testing system developed in Tianjin University is used to test the shock properties of concrete materials,as shown in Fig.2 and schematically depicted in Fig.3.This system mainly consists of a gas gun, a projectile, a high-pressure tank, a vacuum pump and measurement systems.The gas gun with a 152 mm bore and about 9 m barrel length is capable to accelerate the projectile to the maximum velocity of 1500 m/s.As shown in Fig.4,the flyer plate made of duralumin LY12 and the polyethylene project support glued on the flyer plate form the projectile.The target specimen is composed of three concrete pancakes and a backing plate made of LY12 glued together.Before the test,the gun barrel is vacuumed to reduce the air resistance to the projectile.In the test,the projectile is driven by the high pressure gas to move at a high speed in the gun barrel.When impact happens, the stress waves are generated and propagate forth and back through all plates.In the fly plate impact tests, the thickness is much thinner than the section size of the specimen as the specimen is designed as Ф50×8 mm,Ф100×10 mm.Under the shock loads,the specimen can be assumed to be interfered only by axial strain, while the lateral strain is very small.Meanwhile,because the influence of the Poisson’s effect,a three-dimensional stress state is produced in the concrete pancake specimens [22].The different impact velocity of projectile can produce different stress histories in concretes.For the tests,the impact velocities of the projectile VPare between 700 m/s to 1200 m/s which are measured by a laser velometer system.The longitudinal stresses σ (considered to be equal to pressure P) are measured by the manganin stress gauges embedded between the concrete pancakes as shown in Fig.4.Under shock loads,the gauge changes its electrical resistance with the stress and the voltage(ΔU)can be measured and recorded in time by the data acquisition system, and then the longitudinal stress can be obtained by

where R0is the initial resistance of the manganin stress gauge and in this tests is around 50 Ω,ΔR is the changed value of the resistance of the manganin stress gauge during the loading process, GPa.

In order to get the P-ρ relation of concretes under shock loads,the shock velocity D and the particle velocity μ in Eq.(5)should be calculated.The shock velocity D can be measured easily as follow,

Fig.2.The fly-plate impact testing system in Tianjin University.

where Δt is the arrival time between two longitudinal gauges,h is the known distance between the two gauges and is equal to the thickness of the specimen.As for the particle velocity μ, it can be calculated by Eq.(4) (σ = P1= ρ0Dμ) on the premise that the pressure P1is recorded by the manganin stress gauge.Finally,the Pρ relation can be obtained by Eqs.(6) and (7).

2.3.Specimen preparation

In order to study the size effect on the shock properties of concretes in fly-plate impact tests,three sizes of concrete pancakes with the diameters of 150 mm,100 mm and 50 mm are prepared,as shown in Fig.5.All the specimens with different sizes are from the same batching to reduce the uncertainty from the properties of raw material and the curing conditions.Because of the size limitation of the specimen used in fly-plate impact tests, the maximum aggregate size usually ranges from 4 to 8 mm[16,20],and in this test the maximum aggregate size is 6 mm.The cement type is Portland 42.5R.Table 1 gives the mix of the concrete used in this study.To assure the dense quality of the tested specimens, fresh concrete is poured into the mould and vibrated layer by layer.All the specimens are wrap-cured for the first 24 h.After removal of the mould,they are cured in a standard moist chamber with relative humidity of more than 90% and temperature of around 20°C for more than 28 days until the moment of tests.For this test,three dimensions of cured cylinders are prepared, namely, Ф50 × 100 mm,Ф100 × 100 mm, Ф150 × 300 mm.The different expected sized concrete pancakes are obtained from each cured cylinder by cutting to required thickness precisely.In order to meet experimental requirements and obtain accurate data, the surfaces of all concrete pancakes are carefully polished and the error of the parallelism between the two bottom surfaces is controlled to be less than 0.05 mm.In addition,five standard cubic specimens with 150 mm side length have been produced to determine the concrete strength after 28 days and the averaged static compressive strength of these five cubes is 28.8 MPa.The initial apparent density of the specimen is 2.30 g/cm3.

The fly-plate impact tests should satisfy the two fundamental postulates: (a) the shock wave propagating through the target assembly is a plane wave, and (b) the shock wave is uniformly distributed inside the specimen, i.e., the shock parameters of the wavefront do not change with time and distance, which requires the target assembly to meet a certain width-thickness ratio to eliminate the influence of lateral rarefaction wave and longitudinal unloading wave.In this way,the specimen size must be controlled within a certain range to make testing results convincible and the range of thickness varies accordingly to the diameter of the specimen.In general,the width-thickness ratio of the target assembly in the fly-plate impact tests should be greater than 2 and the ratio of target assembly thickness to flyer plate thickness is usually less than 4 [16,25].Besides, the specimen should be large enough to reflect the real properties of the material, which the thickness is designed more thicker of the larger specimen to obtain more accurately compaction process in the tests, and it should be noted that the maximum diameter of the specimen is equal to the diameter of the gun barrel at most, which is equal to 152 mm.In this fly-plate impact tests,three diameters of the concrete pancakes are used in the tests.Table 2 gives the diameters and the thicknesses of the three kinds of testing concrete pancakes which are designed according to the requirements of the study and the postulate.The sizes of the flyer plate and the backing plate are designed on the basis of the concrete pancake.The diameter of the backing plate and the flyer plate are all 150 mm, and their thicknesses are also listed in Table 2.As shown in Fig.4, the target assembly used in the tests consists of 3 pieces of concrete pancakes and one piece of backing plate to help the first gauge to record the stress wave.

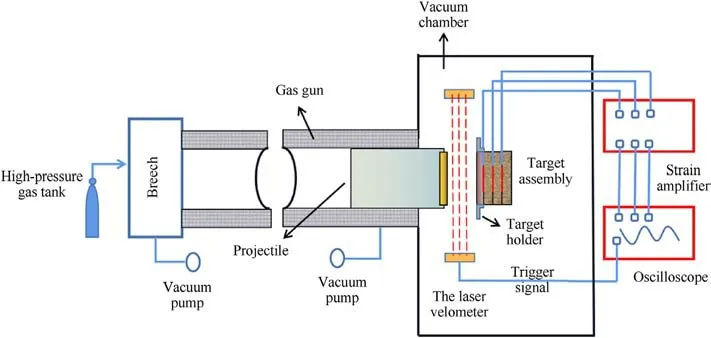
Fig.3.Schematic of the fly-plate impact testing system with measurement systems.

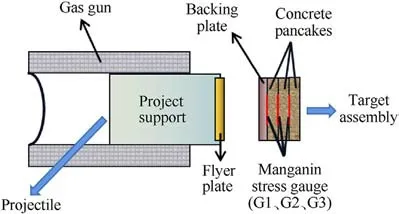
Fig.4.Schematic of the projectile and target assembly.

Fig.5.The specimens used in the tests.

Table 1 Concrete mix proportions.

The prepared target assembly is shown in Fig.6.Three concrete pancakes and one LY12 backing plate are glued together using epoxy one by one and three manganin stress gauges are sandwiched between them.

3.Results and discussion

3.1.The size effect on the recorded shock waves

The experimental parameters and results measured in all the fly-plate impact tests are listed in Table 3.In the fly plate impact tests,the strong shock loading is as high as around 1000 m/s impact velocity and strain rate is of 105-106s-1.In this fly plate impact tests, the strain rate is around 105s-1.The identifier of the specimen C-50-1 means the test record of the first shot of the concrete specimen with a diameter of 50 mm ΔUiis the voltage difference measured by the manganin stress gauges and Δtiis the time of arrival between two longitudinal gauges,the subscript i means the message between the i-th concrete pancake and the (i+1)-th concrete pancake.It should be noted that not all gauges give reasonable signals because sometimes, the signal line and the connections could be interrupted under high speed impact.Fig.7 gives the results of stress histories of different sized specimens tested under nearly the same impact velocity.The identifier of the specimens are the same with that in Table 3,except the last label Giwhich means the i-th manganin stress gauge in a target assembly.For the flyplate impact tests, the strain can be calculated by the following equation,

where ε, ε0is the shocked and the unshocked strain during the impact.As shown in Fig.7, the shock-wave front is divided into a leading elastic precursor and followed by a plastic compressive wave.It can be observed that the elastic precursor rises more and more slowly with the increase of propagation distance, which indicates that the strain rate decreases gradually with the wave propagation.As concrete is a kind of inhomogeneous porous materials, the pore spaces will collapse and the cracks will develop under continuous shock loading.The steeper the slope reflects the faster the compression process under such continuous shock loading.However,the increment rate of the stress is slowed down with the stress wave propagation due to the lateral rarefactioneffect.As for the plastic compressive wave,it can also be seen that the amplitude of the wave attenuates with the wave propagation.From above results, the stress amplitudes including the amplitude of the elastic precursor and the amplitude of the plastic compressive both attenuate to some degree, which are related to the specimen size effect on the shock properties and will be analyzed in the following parts.Besides,it can be seen that the duration of the plastic wave become smaller with the propagation, which can be attributed to the influence of the interference of the lateral stress propagation [38].

Table 2 The three dimensions of the concrete pancakes, the flyer plates and the backing plates used in the tests.

Fig.6.The target assembly with a diameter of 100 mm concrete pancakes:(a)Front of the target assembly; (b) Side of the target assembly.

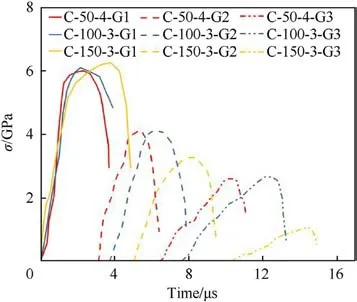
Fig.7.Stress histories measured in the fly-plate impact tests of concrete pancakes with different sizes.

As shown in Fig.7, for the tests of concrete pancakes with different sizes under nearly the same impact velocity, the stresses measured by the manganin stress gauges G1are all about 6 GPa,but with the wave propagation,the stress amplitudes of different sized specimens attenuate in different degrees.This attenuation can be attributed to the following two aspects.On the one hand, it is affected by the longitudinal unloading wave which is controlled by the thickness of the target assembly.In this way,the thinner of the specimen, the reasonable results could be given in the fly-plate impact tests.However, too thin specimen can’t reflect the multimaterial properties of concrete.In most studies, the widththickness ratio of the target assembly is usually greater than 2 and the ratio of target assembly thickness to flyer plate thickness is usually less than 4 [16,25] which can balance the influence of the longitudinal unloading wave and the characteristic of the material.As seen from Table 2, all the specimens in this paper meet these requirements.On the other hand,the lateral rarefaction wave effect can’t be ignored which is related to the specimen size.Table 4 lists the attenuation of the stress amplitude measured in the fly-plate impact tests of different sized specimens in detail.σi-jmeans the stress difference per millimeter along axial direction measured by manganin stress gauge Giand Gj.As shown in Table 4, with the decrease of specimen size, the stress amplitude decays faster per axial length.Under shock loads, the lateral expansion at the freesurface of the concrete target assembly cause interference to the plane shock wave.This lateral rarefaction wave will spread to the center of the target plate at the speed of sound,and thus affects the intensity of the shock wave and bends the shock wave front.The smaller the diameter of the specimen, the stronger the lateral rarefaction interference will be.As listed in Table 4, the stress amplitude of the specimen with a diameter of 50 mm shows significant attenuation due to the influence of the lateral rarefaction interference, while the stress amplitude attenuation of the specimen with a diameter of 100 mm and 150 mm become minimum and are close to each other, indicating the lateral rarefaction wave effect is weaken which can be regarded as an ideal experimental situation.

Table 3 Experimental parameters and results of concrete specimens with different sizes.

Table 4 The attenuation of the stress amplitude measured in the fly-plate impact tests of concrete pancakes with different sizes.

On the other hand, the former study of some scholars [39,40]find that as the increase of the diameter of the cylinder specimen,the lateral inertial force increases which means the material is more likely in a hydrostatic pressure with a minimum deviatoric stress.For the larger specimen,the influence of the shear stress on the EoS properties of concrete could be neglected and give a more convincible result.

3.2.The size effect on the EoS of concrete

From above discussion, because of the influence of the longitudinal unloading wave, especially the lateral rarefaction wave effect and the deviatoric stress produced in the specimen, the specimen size must be controlled within a certain range to make testing results convincible.The larger specimen can better reflect the real properties of concrete material due to the heterogeneity of the specimen (i.e., mortar, aggregates, and interfacial transition zone).After the analysis of the measured information listed in Table 3, the stress, the particle velocity and the shock velocity can be obtained as listed in Table 5.According to the results listed in Table 5 and Eqs.(6) and (7), the Hugoniot states of concrete measured in different sized specimens are shown in Fig.8.The results clearly show that the specimen size obviously influences the Hugoniot properties of concretes measured in fly-plate impact tests.Besides, as can be seen, a larger scatter at lower impact velocities has been shown.This is because under the lower pressure,the porosity and the heterogeneity of the concrete are more remarkable, while when it is compacted to a solid under high pressure,the influence of the material discrete become minor and thus reducing the scatter of the Hugoniot properties in fly-plate impact tests.

As discussed above,the Hugoniot states of concrete measured in fly-plate impact tests are affected by the specimen size.The smaller specimen underestimates the bulk modulus of the concrete which can not accurately reflect the shock properties of concrete.Therefore,the size effect must be considered in the fly-plate impact experiments to predict the EoS of concrete more accurately.In this paper, the influence of size effect become minimum when the diameter of the specimen is reach to 100 mm.Therefore,the testing results of 100 mm specimen and 150 mm specimen are used to calculate the EoS of concrete.The D-μ relation of concretes can be expressed in a linear function by Eq.(5), and thus the Hugoniot state of concretes in D-μ relation can be obtained as follow,

According to Eqs.(6) and (7), the modified Hugoniot state of concretes in P-ρ relation can be obtained as follow,

These functions can be used for the concrete strength around30 MPa and the initial apparent density of the concrete is about 2.30 g/cm3.These functions get from the large specimen tests eliminate the influence of the lateral rarefaction wave effect which can be used to more accurately express EoS of concretes under shock loads.If smaller specimen is used, for example,specimen of 50 mm in diameter may underestimate 20% of bulk modulus.

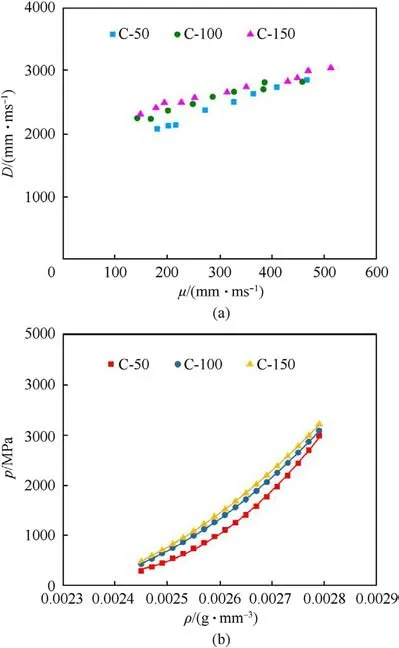
Fig.8.Equation of state of concrete measured in different sized specimens: (a)Hugoniot states: the shock velocity-particle velocity; (b) Equation of state:pressure-density of concrete.

4.Conclusions

This paper carried out a series of fly-plate impact tests to study and quantify the size effect on the shock properties of concretes.The specimens with three sizes are performed to reveal the mechanical background of size effect.The main conclusions can be drawn as follows.

(1) In the fly-plate impact tests, with the propagation of shock waves,the rising rate of the elastic precursor waves become slowly and the amplitude of the waves decays.These phenomena can be attributed to the lateral rarefaction effect which is related to the section size of the specimen and longitudinal unloading effect related to the length of the specimen.

(2) Because of the lateral rarefaction effect, the Hugoniot states of concrete measured in fly-plate impact tests are significantly affected by the specimen size.The small specimen underestimates the bulk modulus of the concrete.

(3) Based on the tests results,specimens with diameter of larger than 100 mm are suggested to use to study the Hugoniot state of concretes in fly-plate impact test.This paper gives and compares Hugoniot state of concretes from 50 mm diameter and 100 mm diameter specimens.Specimen of 50 mm in diameter may underestimate 20%of bulk modulus.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

Funding: This work was supported by the National Natural Science Foundation of China [Grant Nos.51938011 and 51908405]and Australian Research Council.