Data-driven modeling on anisotropic mechanical behavior of brain tissue with internal pressure

Zhiyun Tng , Yu Wng , Khlil I.Elkhodry , Zefeng Yu , Shn Tng ,*, Dn Peng

a State Key Laboratory of Structural Analysis,Optimization and CAE Software for Industrial Equipment,Dalian University of Technology,116023,Dalian,PR China

b The Department of Mechanical Engineering, The American University in Cairo, New Cairo,11835, Egypt

c Department of Neurology, The Second Hospital of Dalian Medical University, Dalian,116023, PR China

Keywords:Data driven Constitutive law Anisotropy Brain tissue Internal pressure

ABSTRACT Brain tissue is one of the softest parts of the human body,composed of white matter and grey matter.The mechanical behavior of the brain tissue plays an essential role in regulating brain morphology and brain function.Besides, traumatic brain injury (TBI) and various brain diseases are also greatly influenced by the brain's mechanical properties.Whether white matter or grey matter,brain tissue contains multiscale structures composed of neurons, glial cells, fibers, blood vessels, etc., each with different mechanical properties.As such,brain tissue exhibits complex mechanical behavior,usually with strong nonlinearity,heterogeneity, and directional dependence.Building a constitutive law for multiscale brain tissue using traditional function-based approaches can be very challenging.Instead, this paper proposes a datadriven approach to establish the desired mechanical model of brain tissue.We focus on blood vessels with internal pressure embedded in a white or grey matter matrix material to demonstrate our approach.The matrix is described by an isotropic or anisotropic nonlinear elastic model.A representative unit cell(RUC)with blood vessels is built,which is used to generate the stress-strain data under different internal blood pressure and various proportional displacement loading paths.The generated stress-strain data is then used to train a mechanical law using artificial neural networks to predict the macroscopic mechanical response of brain tissue under different internal pressures.Finally,the trained material model is implemented into finite element software to predict the mechanical behavior of a whole brain under intracranial pressure and distributed body forces.Compared with a direct numerical simulation that employs a reference material model,our proposed approach greatly reduces the computational cost and improves modeling efficiency.The predictions made by our trained model demonstrate sufficient accuracy.Specifically, we find that the level of internal blood pressure can greatly influence stress distribution and determine the possible related damage behaviors.

1.Introduction

Studying the brain and its related pathologies have attracted research attention for a long time.Nowadays, it is recognized that the mechanical behavior of brain tissue plays a vital and irreplaceable role in many related diseases [1].Brain tissue can be divided into white matter and grey matter, composed primarily of two classes of cells:neurons and glial cells[2].The cell bodies of the neurons are distributed in the grey matter, while the bundles of axonal fibers compose the white matter.Axonal fibers then form a complex network,connecting the grey matter's different regions.In grey matter and white matter, blood vessels split into branches of different sizes.The brain's morphology also exhibits gyri and sulci structures that form its complex surface and which strongly relate to intelligence and neurological dysfunction.Natural factors such as cortical and subcortical thickness,neuronal myelination thickness,and stiffness or growth rate can all generate variations in the gyri and their mechanical properties [3-5].Moreover, various pathological changes,such as a sudden increase in blood pressure,may cause cerebral edema and cerebral hemorrhaging,especially in the basal ganglia.Cerebral edema and cerebral hemorrhaging closely relate to the mechanical properties of blood vessels, brain tissue, and blood dynamics [6].Similarly, traumatic brain injury(TBI)is one of the most difficult problems faced by the world today,as a typical mechanics problem,and has been discussed in classical books,e.g.,Ref.[7].Indeed,according to recent statistics,about 5.3 million Americans and about 7.7 million Europeans suffer from TBIrelated diseases [8-10].

Mechanical experiments,often postmortem,must be carried out to investigate the me chanical behavior of brain tissue and uncover the underlying mechanisms related to brain problems such as TBI and physiological disorders such as cerebral hemorrhaging.Based on the experiments, constitutive models should be then constructed,and problem-specific simulations,e.g.,finite elements on TBI,should be performed for further analysis.Over the past decade,several research groups have explored the mechanical behavior of brain tissue through postmortem experiments.However,due to the scarcity of human brain tissue and the limited size of their samples,only a handful of studies have actually tested the mechanical response of human brain tissue[11-15].Thus,most researchers use animal samples such as mice[16],pigs[17-19],or cattle[20,21]to characterize the mechanical properties of brain tissue.It was found that factors such as age [22-25], postmortem time [26-28], and region [20,21,29-33] do influence the measured mechanical behavior of the tissue.Nevertheless, it can be concluded that the overall mechanical response of brain tissue exhibits nonlinearity,anisotropy, heterogeneity [34,35] and strain rate dependence[21,36,37].

Complex mechanical behavior stems from the multiscale microstructure of the tissue, which includes neuronal networks,glial cells, axonal fibers, blood vessels, etc.To capture this complexity in their constitutive models, many researchers have therefore incorporated detailed microstructural information in them[38].For example,to capture Diffuse Axonal Injury(DAI)and brain contusion in white matter, a multiscale framework that considers the axons was put forward, aiming to capture axonal injury as it relates to loading condition, matrix environment, and mechanoporation [39-42].Alternatively, a mesoscale mechanics model was developed to describe the mechanical behavior of white matter, e.g., Ref.[43].The white matter is, in this case, taken as a fiber-containing composite with an isotropic matrix and an anisotropic axonal fiber phase.Compared with experiments, such an approach clarifies the mesoscale mechanisms of nonlinear, anisotropic, and strain rate-dependent behavior of brain tissue.

We note that blood vessels are distributed in the extra-cellular matrix of the brain tissue in grey and white matter.Blood flow controls material transport across the brain and may influence its mechanical behavior, and function [44].At the same time, blood pressure also plays a vital role in the growth and development of brain tissue [45].To our best knowledge, blood vessels and their associated internal pressure have not been considered in previous works.However,the absence of blood vessel pressure is one of the main reasons for the different mechanical responses of brain tissue in-vivo and in-vitro.The flow of blood in the vessels can also amplify viscous deformation(rate-dependent behavior).Therefore,it is particularly important to capture the effect of internal pressure and blood flow on the mechanical behavior of brain tissue.

In this paper, we seek to capture the mechanical behavior of brain tissue with consideration of the blood vessels as microstructural elements.Many previous works have relied on mathematical derivations, complex numerical implementations, and the multiplicity of material parameters lacking direct physical meaning.To overcome these limitations,we propose a data-driven approach.With the development of data science in recent years,many data driven (or machine learning) methods have been proposed and successfully used to predict the macroscopic behavior of multiscale microstructured composites.For instance,the method of neural networks was adopted to fit a mapping function between stress and strain for isotropic nonlinearly elastic materials[46-51].In addition to artificial neural networks (ANN), other methods based on machine learning techniques,such as clustering were also proposed, e.g., a self-consistent clustering analysis (SCA) approach[52,53],a virtual clustering analysis(VCA)approach[54],and FEMcluster based analysis (FCA) approach [55].

Thus, a data-driven approach is developed in this paper to characterize the role of blood vessels in brain tissue and the effect of their internal pressure on its mechanical response.First, a representative unit cell (RUC) with blood vessels in the microstructure is set up.Then,different loading paths are applied to the RUC to generate stress-strain data.We do not assume that the macroscopic response of the RUC is isotropic but instead consider the directional dependence of brain tissue.Then,an artificial neural network (ANN) is trained to encode the constitutive law for the macroscopic behavior of the tissue.For training,the internal blood pressure and the Green strain are used as the inputs,and the second Piola-Kirchhoff stress is obtained as the output.The trained model is then applied to simulate brain tissue deformation under intracranial pressure and distributed body forces.

This paper is organized as follows.Section 2 introduces offline data generation and training.Online computation with the trained model is also proposed.The results for modeling the brain tissue under the intracranial pressure and distributed body force are shown in Section 3.Our conclusions are given in Section 4.

2.Framework of the data-driven approach

A flowchart of our proposed data-driven approach to blood vessel-containing brain tissue is shown in Fig.1.It can be divided into two parts:The offline stage and the online stage.In the offline stage, an RUC containing vascular structures is set up to represent brain tissue as a complex composite material with blood vessels that split into branches of different sizes.The size of a blood vessel is considerably smaller than that of the whole brain,satisfying the scale-separation condition required for using an RUC.Subsequently,a homogenization method can be used to obtain from the RUC the macroscopic mechanical properties of the composite brain material.In this manner,the influence of the brain's microstructure on its macroscopic mechanical properties can be obtained.

Microscopic stress-strain data is thus generated by direct numerical simulation of the RUC, subjecting it to many different loading paths.In these simulations, the internal pressure p is imposed on the inner surface of the vascular structures.ANN is subsequently used to train a macroscopic (homogenized) material law on the stress-strain data obtained from the multiple RUC cases generated.This completes the offline stage.

For the online stage, our trained macroscale material law (for homogenized brain tissue) is implemented into finite element software and used to predict the mechanical behavior of a halfbrain model loaded by intracranial pressure and distributed body forces.

2.1.Mechanistic considerations

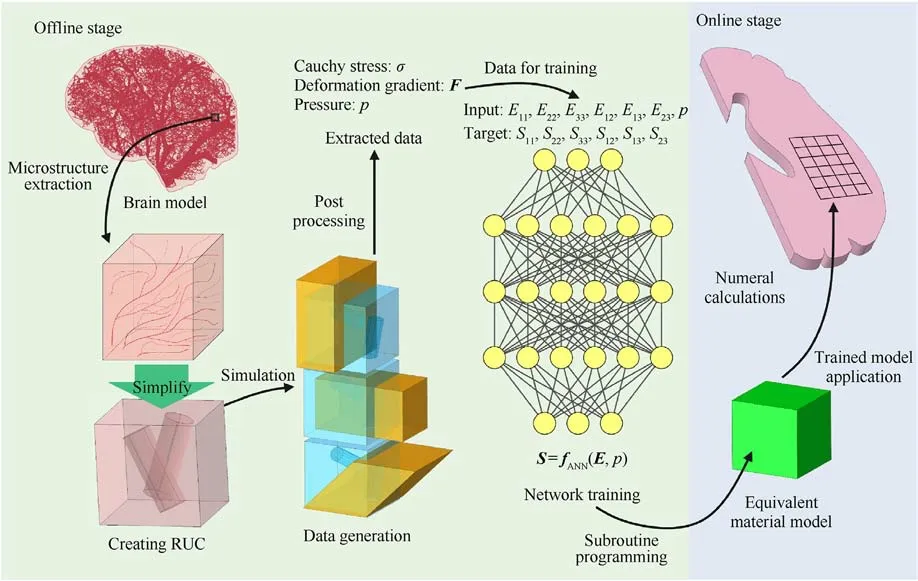
Fig.1.A summary of the data-driven approach to model the brain tissue with the microstructure of blood vessel.

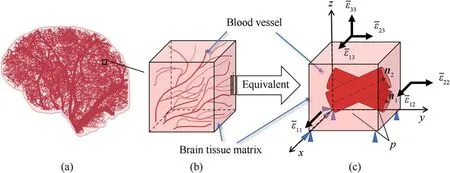
Fig.2.(a)Schematic diagram of the distribution of capillaries in human brain tissue;(b)Tissue models containing microstructures randomly extracted from brain tissue structures;(c) Equivalent material model with cavities that simplifies capillaries in tissue models.

Our aim is to build a macroscopic material law from the RUC shown in Fig.2 using an efficient, mechanistically enhanced datadriven approach.As discussed in the introduction, the macroscopic law is mechanistically assumed to admit nonlinear,heterogeneous, and anisotropic (direction-dependent) behaviors consistent with the brain tissue's measured properties.However,strain-rate dependence is ignored here, which would require an advanced machine-learning tool.A rate-dependent extension of this work will be reported on in a later publication.We now show how to build the nonlinear,anisotropic material law from the RUC.In continuum mechanics,the deformation gradient F represents the mapping between the initial and current configurations.When the material deforms, the point at X in the original configuration will move to the point of x in the current configuration, The deformation gradient is thus defined as

Corresponding to E is the second Piola-Kirchhoff stress (S),which is constitutively determined.The Cauchy stress σ in the current configuration (true stress) can then be obtained using

If we generate from each RUC the dataset (E11, E22, E33, E12, E13,E23,p)as input for the ANN,and the corresponding set{S11,S22,S33,S12, S13, S23} as the output to be learned, the mapping fANNcan be trained to obtain the desired macroscopic material law.We emphasize that E and S should be the apparent (homogenized)quantities derived from the RUC.

2.2.Offline: data generation

This subsection discusses how stress-strain data (S and E) is generated based on the RUC.The five main aspects of the RUC are thus outlined.

RUC Geometry:Brain tissue possesses one of the more complex microstructures in the human body.This paper only focuses on the intravascular pressure's effect on the tissue's mechanical behavior.As noted earlier, blood pressure is important for pathological diseases such as brain edema or cerebral hemorrhage.As such,in the RUC, brain tissue microstructure,aside from vascular structures,is captured as a homogeneous matrix.Building the RUC with blood vessels inclined at a known angle is then straightforward.A cubic RUC 1 mm×1 mm×1 mm is established as shown in Fig.2(c).Two randomly generated blood vessels are thus introduced into the RUC cube (by a Boolean operation), featured as two cylindrical voids whose volume fraction is 10%.The center points for the starting planes of these two blood vessels are located at (0.25, 0.50, 0.50)and (0.75, 0.50, 0.50).Their central axis vectors are n1= (0.05,0.72,-0.34)and n2=(0.02,0.76,0.25).Blood vessel radius is set to 0.141 mm.

RUC matrix material law: Due to the nonlinear characteristics of brain tissue, the Ogden model ([56]) has been widely used in Ref.[43].We thus model the matrix of our RUC using the Ogden model, which ignores matrix anisotropy for simplicity.The strain energy per unit volume is thus given by

RUC boundary conditions: Periodic boundary conditions are applied to the RUC.With periodic conditions the displacements ui of the points on the boundary can be expressed as [57]

where tiis the surface traction vector at a point on the outer surface of RUC, which can be extracted directly from finite element software.The macroscopic average Green strain is

where J = det（F）.

2.3.Offline: ANN structure and training

After the stress-strain data are generated, an artificial neural network builds a latent constitutive model from the brain tissue.In this paper, to consider an anisotropic mechanical response, six Green strain components and the intravascular pressure (totaling seven parameters) are used as input for the ANN, and the six components of the second Piola-Kirchhoff stress are the output.To ensure efficiency and accuracy, a 7-layer network architecture is adopted,in which the five hidden layers have 24,24,24,24,and 12 neurons, respectively.The overall architecture of the adopted neural network is shown in Fig.3.The activation function is a sigmoid function.The number of training iterations is 1464 steps.The mean squared error (MSE) is used to evaluate the performance of ANN training.The training error vs.the epochs is plotted in Fig.4(a).Fig.4(b)showing the trained ANN's generalizability as measured by the correlation coefficient on the test set; i.e., a correlation coefficient of close to 1 demonstrates that the trained model is accurate.

2.4.Online computation

The trained model can be implemented directly into finite element software (commercial or in-house) as a material subroutine.In the online stage, each integration point can obtain the deformation gradient Fnat an incremental step n.Then, the Green strain Enat that point can be computed by Eq.(2).For the given internal pressure, the second Piola-Kirchhoff stress Sncan be computed from the trained neural network.

Then the Cauchy stress σn can be obtained by Eq.(3).The tangent modulus should be supplied for a stress update with an implicit solver to ensure fast convergence.The tangent modulus tensor corresponding to the second Piola-Kirchhoff stress and the Green strain can be obtained as

3.Results and discussion

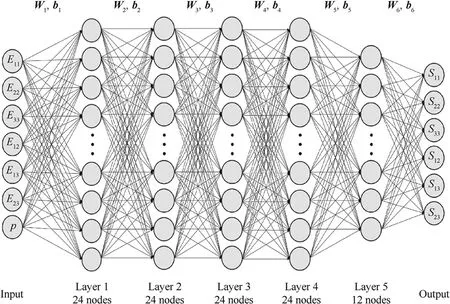
Fig.3.Schematic diagram of artificial neural network structure in the present work.

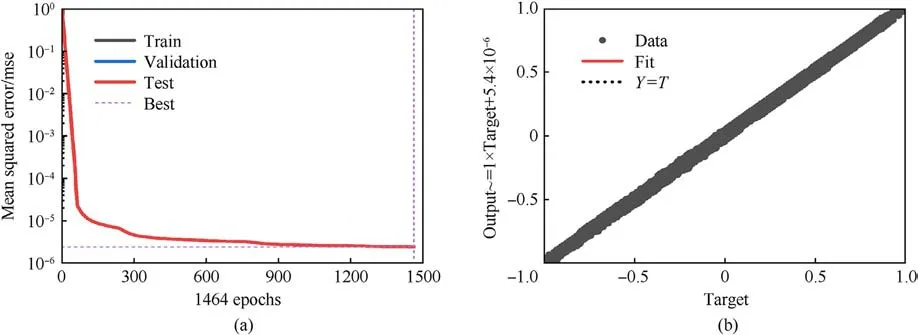
Fig.4.(a) The training error vs.the epochs.Best valiadation performance is 2.4161e-6 at epoch 1464; (b) The correlation coefficient of test sets R, R = 0.99997.

In this section, the predictions made by the trained model are compared with direct numerical simulation (DNS) to verify the validity of the proposed approach.The trained model is used to simulate a hemisphere of brain tissue, to capture the effect of intravascular pressure on the mechanical response of brain tissue,and demonstrate its importance.In all cases, the units of measure remain the same.The unit of length is mm;the unit of force is mN;the unit of stress,pressure,and modulus is kPa,and of density is kg/mm3.

3.1.Model validation

We first validate the proposed approach using the stacked nine 1 mm×1 mm×1 mm RUC models containing vascular microstructures shown in Fig.5(a).The entire computational domain is 3 mm×3 mm×3 mm.At the same time, a corresponding homogeneous model with the vascular microstructure smeared out is also set up.Under an intravascular pressure of 0.2 kPa, the DNS model and the trained homogenized model are subjected to uniaxial tension, uniaxial compression, pure shear, and biaxial loadings, respectively.The biaxial loadings are applied in two ratios,ε11:ε22=1:-1 andε11:ε22=1:1.The loading situation of each working condition is shown in Fig.6.The corresponding stressstrain responses predicted by DNS and the trained model under uniaxial tension and compression are shown in Fig.7(a),under pure shear in Fig.7(b),under biaxial loading with a loading ratio ofε11:ε22=1:-1 in Fig.7(c) andε11:ε22=1:1 in Fig.7(d).In these figures, the blue squares or red dots represent the mechanical responses predicted by the DNS model,while the blue or red lines represent those predicted by the trained model under the same loading conditions.It can be observed that the prediction of the trained model is in good agreement with that of DNS, and the maximum error does not exceed 2%.At the same time,Fig.7(d)also shows the brain tissue's captured anisotropic mechanical properties resulting from the vasculature.It can be concluded that under typical loading conditions, such as uniaxial tension-compression,pure shear, and proportional biaxial loading, the trained model performs very well.It can also be seen that the mechanical response under tension is different from that under compression,which is consistent with the experimentally measured properties of brain tissue [60].

We then rotate some of the cells 90°about the z-axis to simulate a disordered vascular microstructure,as shown in Fig.5(b).Uniaxial stretching,uniaxial compression,and pure shear are applied to the DNS and the trained model simultaneously.Fig.8 shows the corresponding mechanical response curve.In the disordered vascular structure, the training model can still predict the mechanical behavior of brain tissue well,and the maximum error is controlled within 7%.This also implies that the trained model shows the potential to capture the important physical properties of brain tissue.

In addition, in this validation example, the online computation for the DNS took 11.5 h.The trained ANN model took only 180 s(online stage) for the same computing resources.It is evident that the computational efficiency of the model is greatly improved without losing accuracy.

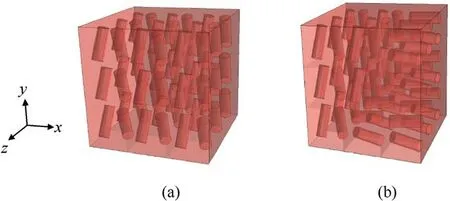
Fig.5.The 3 mm×3 mm×3 mm models with (a) vascular microstructures and (b) simulated disordered vascular microstructures.

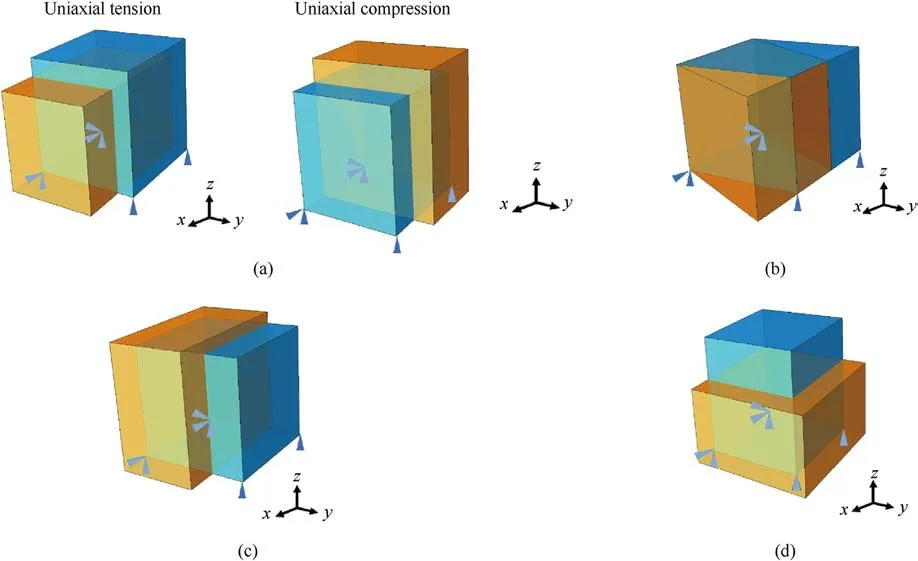
Fig.6.(a) Uniaxial tension and compression; (b) Pure shear; (c) Biaxial loading with a loading ratio of ε22 :ε33 =1:-1 and (d) Biaxial tensionε22 :ε33 = 1:1.

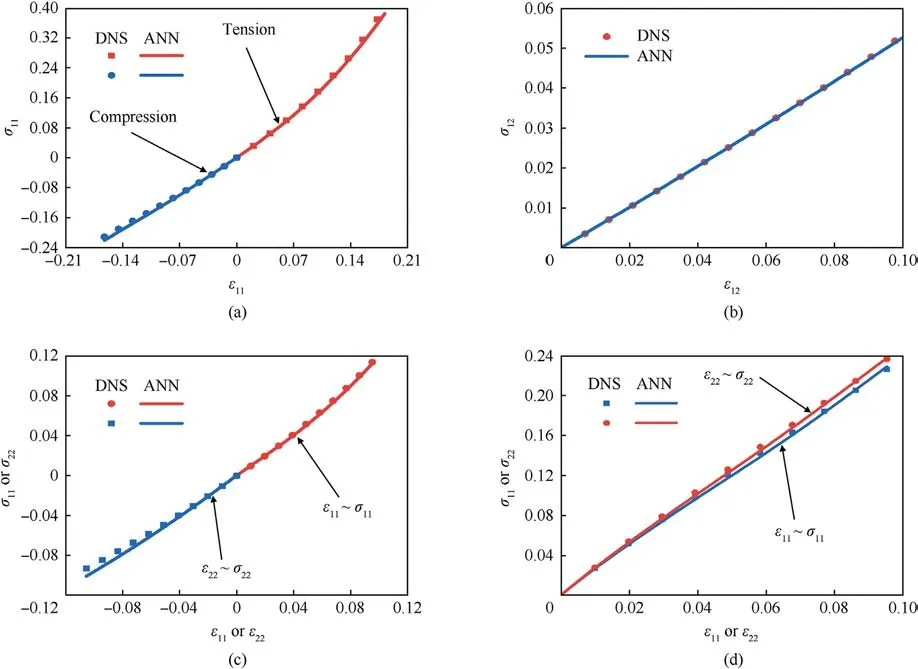
Fig.7.The mechanical response curves of the 3 mm×3 mm×3 mm models with vascular microstructures:(a)Uniaxial tension and compression;(b)Shear;(c)Biaxial tension ε11 :ε22 = 1: - 1; (d) Biaxial tensionε11 :ε22 = 1:1.

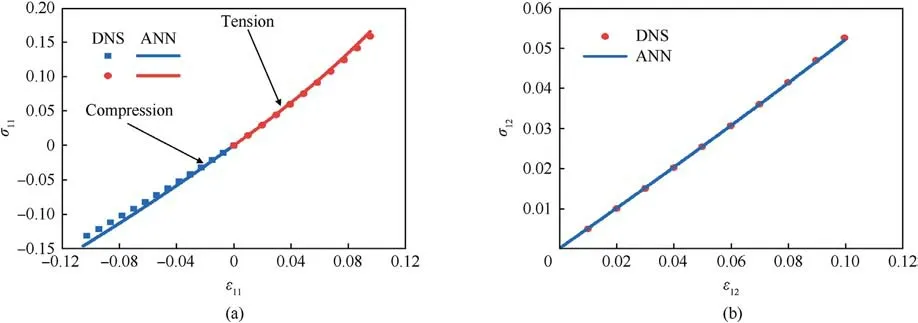
Fig.8.The mechanical response curves of the 3 mm×3 mm×3 mm models with disordered vascular microstructures: (a) Uniaxial tension and compression; (b) Shear.

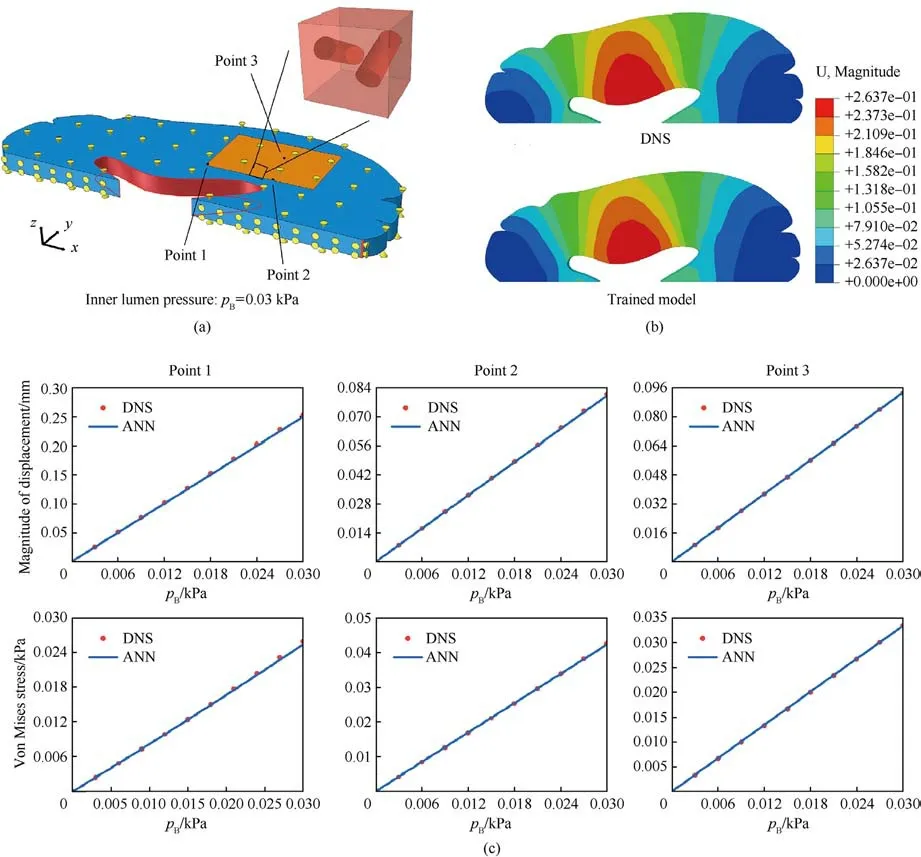
Fig.9.(a)The slice of the brain tissue with 1 mm thickness for modeling.The red area is modeled by both DNS and the trained model;(b)Displacement contours predicted by DNS and the proposed approach under the inner lumen pressure pB=0.03 kPa.The blood pressure is set as 0.05 kPa;(c)The variation of displacement,Von Mises stress vs.the imposed lumen pressure at three points marked in Fig.9(a).

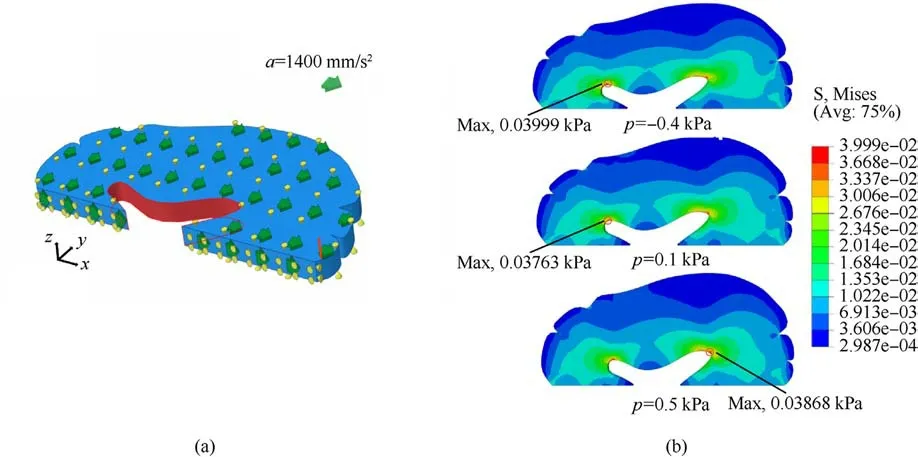
Fig.10.(a)The slice of the brain tissue with 1 mm thickness for modeling;(b)The contour plot of stress for the brain tissue under the action of inertial force in the x-direction with the intravascular pressure of -0.4 kPa, 0.1 kPa and 0.5 kPa.The maximum stress is marked by the black circle.

3.2.Brain tissue modeling

Having completed model validation,we attempt to simulate the brain with the trained model directly.A slice of the right hemisphere with 1 mm thickness is considered, shown in Fig.9(a),which is modeled in our simulations.We still adopt two approaches to model the deformation of brain tissue: DNS and the proposed approach in this work.Needless to say,if all the blood vessels in the brain slice are explicitly captured, the computational cost will become unfeasible.Thus, only in the orange region shown in Fig.9(a),the vascular microstructure is directly modeled.The other parts of the brain tissue are modeled by the trained model.Conversely, for our proposed approach, all brain tissue is modeled by the trained model.For both DNS and the proposed approach,the degree of freedom of the middle line(the x-axis)in the y direction is held fixed.The X direction of the upper and lower surfaces of the slice is further fixed.To avoid rigid body displacement, the x direction of one end is also fixed per Fig.9(a).For both DNS and the proposed approach, the internal pressure of blood vessels is set to 0.05 kPa.A pressure of pB=0.03 kPa is imposed in the inner lumen of the brain tissue as the external loading.Fig.9(b) plots the displacement contours of DNS and the proposed model under this condition.It can be observed that the results predicted by the trained model are in good agreement with the DNS model.We randomly selected three nodes in two model rows for displacement and Mises stress analysis.The corresponding graph is shown in Fig.9(c).The ordinates in the figure are displacement and Mises stress,and the abscissa is the pressure exerted on the luminal cavity of the brain tissue.It can be observed that the prediction results of the trained model can fit the DNS19 prediction results well.The maximum error of the two models does not exceed 2.16%.This example shows that the proposed method shows good potential for accurately capturing mechanical deformations of brain tissue,even with realistic and larger scale geometries.

3.3.Internal vascular pressure effect under pseudo-impact

Finally,the trained model is adopted to simulate the mechanical response of a hemisphere of brain tissue with internal pressure from the embedded blood vessels.Since the effectiveness of the trained model to describe the anisotropic behavior with internal pressure has been verified in the previous examples, it will be directly used to model brain tissue under different blood pressures.Using our proposed approach would save much computational time to perform a parametric study compared to DNS.Here three levels of internal pressure of blood vessels are considered:-0.4 kPa,0.1 kPa,and 0.5 kPa.The displacement in the inner lumen of the brain tissue(i.e.,the orange area of Fig.10(a))is fixed in the x direction.At the same time, a gravitational acceleration of 1 mm/s2,400 mm/s2in the x-axis direction was applied to the brain tissue as a body force,which is used to mimic the inertial force generated by the impact.The degree of freedom of the middle line (the x-axis) in the y-direction is fixed.The X-direction of the upper and lower surfaces of the slice is further fixed.Fig.10(b)plots the contours of Mises stress under the three levels of the internal vascular pressures:-0.4 kPa,0.1 kPa,and 0.5 kPa.The places with the maximum stress are marked by black circles.From Fig.10(b),it can be observed that when the intravascular pressure is 0.1 kPa,the maximum Mises stress of brain tissue occurs in the left lumen with a value of 0.03763 kPa.When the blood pressure becomes-0.4 kPa,the maximum Mises stress in the left inner lumen increases to 0.03999 kPa.Compared with 0.1 kPa, the maximum Mises stress increased by 6.3%.When the intravascular pressure increases to 0.5 kPa,brain tissue's maximum Mises stress position is transferred from the left to the right-brain cavity.It can be concluded that different blood pressures have different effects on the pressure caused by impact, which is consistent with intuition.Because trained models can greatly reduce computational costs, more underlying mechanisms can be explored in silico, and more simulations can reveal further insights.

4.Conclusions

This paper proposed a mechanistically informed data-driven approach to predict brain tissue's vasculature-induced anisotropic mechanical response.We first construct an RUC for brain tissue considering blood vessels, on the surface of which the internal blood pressure is imposed.Through a homogenization method,macroscopic stress and strain data can be generated.Then,the data is trained by using ANN to represent a macroscopic constitutive law for brain tissue.The internal pressure and the Green strain components are inputs for ANN, and the second Piola-Kirchhoff stress component is the output.Effects of the internal pressure on the macroscopic mechanical behavior of brain tissue can be captured effectively.The prediction of our trained model has been validated by a reference model and DNS.Our trained model can greatly save computational costs and can effectively conduct parameter studies to explore blood pressure-related pathologies.Our preliminary results suggest that internal blood pressure affects the maximum pressure distribution under shock.However,because brain tissue is a biological material with a complicated microstructure, its neurons,glia,and extracellular matrix,were homogenized in this study[43].At the same time, the viscosity of the blood and the cyclic loading associated with it are not captured.These simplifications are adequate for our intended modeling objectives but leave much room for future research.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The support of the Project MKF20210033 is acknowledged.