基于格的访问控制加密技术研究
谭高升 李 伟 马静静 王伟忠 邢建华 马明杰
1(北京京航计算通讯研究所 北京 100074)
2(军事科学院系统工程研究院 北京 100101)
3(中国工业互联网研究院 北京 100102)
访问控制加密[1](access control encryption, ACE)是一种功能性公钥加密,不仅可以控制谁有权限阅读消息(读权限),还可控制谁有权限发送消息(写权限).控制读权限是传统公钥加密,例如基于身份的加密[2-4]、基于属性的加密[5-7]等具备的特点,即只有拥有解密私钥的接收者可以阅读加密消息.几乎所有的传统公钥加密都未考虑控制消息的写权限.在一些通信系统中控制写权限是一种非常重要的需求,尤其在具有多个安全等级的通信系统中.
文献[1]构造了基于DDH(decisional Diffie-Hellman)假设的访问控加密方案,但是,文献[8]指出此方案存在密文泄露攻击(即无发送权限的攻击者可以通过获取有发送权限人员生成的密文,从而取得相应的发送权限).存在这种攻击的根源在于文献[1]中的安全模型存在局限性.文献[8]提出了角色遵守安全性模型(role respecting security model),文献[1]方案满足此安全模型即可抵抗密文泄露攻击.文献[8]基于Naor-Yung构造策略[9]利用非交互零知识证明[10]和同态公钥加密[11]构造了CCA安全的方案.但是,文献[2]并未修补文献[1]中的DDH方案,文献[2]提出的构造方法很难直接应用于DDH方案,由于非交互零知识证明使得方案既复杂又低效,方案的通信策略受到限制.构造高效的满足任意通信策略的CCA安全的访问控制加密方案是文献[2]中的公开问题.
本文主要贡献如下:首先将文献[1]中的DDH方案进行了通用化设计,并以非常高效的方式修补了方案易受密文泄露攻击的不足.其次,提出了一种通用、高效、满足任意通信策略的CCA安全的访问控制加密方案,并能够基于多种标准假设实例化,包括基于格上困难性假设,因此,本文方案还具备后量子安全性(post quantum security).最后,分别基于带错学习(learning with error, LWE)[12]与短整数解[13]假设(short integer solutions, SIS)和DBDH假设[14]给出了CCA安全方案的2种实例化构造.本文主要贡献如下:
1) 抗密文泄露攻击的高效CPA安全方案.本文将文献[1]的DDH方案进行了通用化设计,并基于满足同态性质的公钥加密与伪随机函数构造了CPA安全的抗密文泄露攻击的访问控制加密方案.如果方案同样基于DDH假设进行实例化,本文方案与初始DDH方案相比同样高效,均有相同的密文长度,唯一的额外开销是关于伪随机函数的计算开销.
2) 满足任意通信策略的通用高效CCA安全的访问控制加密方案.本文利用基于身份加密(identity based encryption, IBE)、强一次签名(strong one-time signature, SOTS)和伪随机函数构造了通用的CCA安全访问控制加密方案.受到文献[15]中的变换(CHK-变换)启发,本文利用CHK-变换构造的CCA方案效率更高.在本文方案中,密文的基础形式为c=(vk,c1,c2,σ),其中vk是强一次签名的认证密钥,c1和c2是IBE的密文,σ是(c1,c2)作为消息生成的签名.发送权限的控制原理是存在1个信道控制器,其对签名进行验证,如果签名有效,则对(vk,c1,c2)进行处置,生成发送给接收者的密文c′.需要注意,CCA安全性只针对密文c,c′无法满足CCA安全性.
3) 基于格假设或DBDH假设下方案实例化.本文给出2种通用CCA安全方案的实例化构造:一种基于LWE和SIS假设,满足后量子安全性;另一种基于DBDH假设,效率更高.方案构造的关键在于IBE方案需满足特殊的性质,本文称为身份变换不可区分性(参见定义1),本文证明文献[13-14]中的IBE方案均满足身份变换不可区分性.
文献[1]还提出了满足任意通信策略条件下密文长度可以是多项式对数(polylogarithmic)复杂度(关于通信系统中用户数量)的方案,但是,此方案需要基于不可区分性混淆(indistinguishability obfuscation, IO).文献[10]基于标准的双线性对假设,提出了密文长度同样为多项式对数复杂度的方案,但是此方案的通信策略受限,不能满足任意的通信策略.文献[16]提出了基于标准化假设的访问控制加密方案,其方案密文长度满足多项式对数复杂度且可以满足任意通信策略.方案构造过程使用了数字签名、谓词加密(predicate encryption)和单密钥函数加密(functional encryption),为了实现写权限控制,函数加密需要支持随机化函数(randomized functionality)[17-18].文献[19]提出了基于LWE假设的访问控制加密方案.以上所有方案只满足CPA安全性.表1给出了本文方案与相关方案的对比结果:

表1 本文方案与相关方案的对比结果
本文方案同时满足抗密文泄露攻击、后量子安全性、任意通信策略.虽然密文的长度复杂度为多项式级别,考虑实际系统通信带宽的提升,本文方案因构造简单同样具有实用价值.
1 基础知识
基于身份的加密:基于身份的加密方案IBE由4个算法构成,记作(KGI,ExtI,EncI,DecI),本文的IBE方案需要满足身份可变性.记IBE.CONVERT(·,·)为概率性算法,称为身份变换算法,输入身份id和以id为公钥的密文c,输出1个“新的”身份id′和id′为公钥的密文c′,记作(id′,c′)←IBE.CONVERT(id,c),且满足如下要求.
定义1.身份变换不可区分性.记λ为安全参数,IBE为基于身份的加密方案.记ID为IBE的身份空间.U(ID)表示ID空间上的均匀分布.称IBE满足身份变换不可区分性,如果存在多项式时间算法IBE.CONVERT(·,·),任取(id,c)∈ID×Cid,记解密算法解密结果m=DecI(skid,id,c),生成(id′,c′)←IBE.CONVERT(id,c),满足:
1) 输出身份id′的分布Did′与U(ID)计算不可区分;
2) 密文c′与c具有同等的安全强度且m=DecI(skid′,id′,c′).
满足身份不可区分性的IBE将作为本文方案构造的基础之一,构造CCA安全的公钥加密方案.并且,在方案实例化中,本文将提出2种满足身份变换不可区分性的IBE,分别基于格假设与基于DBDH假设.
访问控制加密:ACE由5个多项式时间算法构成,记作(Setup,KG,Enc,San,Dec).初始化算法为概率性算法,记作(pp,msk)←Setup(1λ,PL),其中,λ为安全参数,PL:[n]×[n]→{0,1}为通信策略,PL(i,j)=1表示用户i可以给用户j发送消息,否则表示不允许发送,pp表示公共参数,后续算法都会默认包括公共参数;密钥生成算法为概率性算法,记作k←KG(msk,i,t),其中i∈{0,1,…,n+1}表示用户的身份,0表示空身份,n+1表示信道控制器身份,t∈{sen,rec,san}表示身份属性,分别为发送者、接收者和信道控制器,k∈{eki,dki,rk}分别表示加密密钥、解密密钥和重随机化密钥;加密算法为概率性算法,记作c←Enc(eki,m),eki为加密密钥;密文重随机化算法为概率性算法,记作c←San(rk,c),rk为重随机化密钥;解密算法为确定性算法,记作m′←Dec(dkj,c′),dkj为解密私钥.
访问控制加密正确性指对任意合法生成的密钥eki,dkj,如果PL(i,j)=1,则解密失败的概率Pr[m′≠m]≤negl(λ),即为关于安全参数的可忽略函数.访问控制加密的安全性定义包括选择明文攻击下的不可读规则(no-read rule, NR)、不可写规则(no-write rule, NW)与角色关联性(role-respecting, RR),分别记作NR-CPA,NW-CPA,RR-CPA,其中,不可读规则根据安全目标,分为密文负载机密性(payload privacy, PP)发送者匿名性(sender anonymous, SA),分别记作PP-CPA,SA-CPA;进一步,包括选择密文攻击下的不可读规则、不可写规则与角色关联性,分别记作PP-CCA,SA-CPA,NW-CCA,RR-CCA.本文将提出分别满足2种安全性的访问控制加密方案.
2 通用方案构造
本节分别给出CPA安全通用方案构造与CCA安全通用方案构造.
2.1 CPA安全通用方案构造
本节主要构造针对单用户系统的访问控制加密方案,即系统中只有1个发送者、1个接收者和1个信道控制器,针对多用户系统,可以通过并行执行多个单用户加密方案实现多用户系统方案构造,记单用户访问控制加密方案为1-ACE.1-ACE方案由同态公钥加密方案和伪随机函数构造而成,记同态公钥加密方案PKE为(KGP,EncP,DecP),满足IND-CPA安全性,密文间的同态运算记作“+”.记伪随机函数为Fkprf(·),其中kprf为伪随机函数密钥.令伪随机函数的定义域为PKE的密文空间CP,值域为PKE的明文空间MP.1-ACE方案构造如下:
1) (pp,msk)←Setup(1λ,PL).输入安全参数λ和系统通信策略PL:{0,1}×{0,1}→{0,1},初始化算法调用同态公钥加密密钥生成算法(skP,pkP)←KGP(1λ)和伪随机函数密钥生成算法kprf←KGprf(1λ),输出1-ACE方案的主私钥msk=(skP,kprf)和公共参数pp=(pkP,PL,λ).
2)k←KG(msk,i,t).输入主私钥msk,编号i∈{1,2}和角色t∈{sen,rec,san},密钥生成算法如下:
① 对于输入(msk,1,sen),输出发送者加密密钥ek1=kprf;
② 对于输入(msk,1,rec),输出接收者解密密钥dk1=skP;
③ 对于输入(msk,2,san),输出信道控制器的重随机化密钥rk=kprf.
3)c←Enc(ek1,m).输入加密密钥ek1和消息m,计算c1=EncP(pkP,m)与c2=EncP(pkP,Fkprf(c1)),输出密文c=(c1,c2).
4)c′←San(rk,c).输入重随机化密钥rk和密文c,算法选择1个随机整数r,计算密文c3←EncP(pkP,Fkprf(c1))与密文同态计算结果c′=r(c2-c3)+c1,输出重随机化密文c′.
5)m′←Dec(dk1,c′).输入解密密钥dk1和密文c′,调用解密算法m′←DecP(skP,c′),输出消息m′.
规定:如果PL(i,j)=0,即发送者i不允许给接收者j发送消息,则发送给j的密文为从密文空间随机选择的密文.
关于方案正确性,如果对于合法生成的公钥和私钥,同态公钥加密可以正确解密同态计算后的密文,则1-ACE方案同样可以正确解密.
1-ACE方案CPA安全性:记λ为安全参数、PL为通信策略,如果同态加密方案PKE满足选择明文攻击下不可区分安全(IND-CPA)且函数Fkprf(·)满足伪随机安全性,则构造的1-ACE方案满足NR-CPA,NW-CPA,RR-CPA安全性.具体地,对于任意攻击1-ACE方案的敌手A,假设其运行时间为T,则存在攻击公钥加密方案PKE的敌手A′,满足
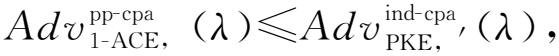
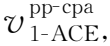
2.2 CCA安全通用方案构造
在CCA安全通用方案构造中,同样以构造单用户访问控制加密方案为主.记基于身份的加密方案IBE为(KGI,ExtI,EncI,DecI),且具有同态性质,记IBE方案的身份变换算法为IBE.CONVERT(·,·),同态计算符号为“+”.记SIG=(KGS,S,V)为强一次签名方案(strong one-time signature),Fkprf(·)为伪随机函数.满足CCA安全的1-ACE方案构造如下:
1) (pp,msk)←Setup(1λ,PL).输入安全参数λ和系统通信策略PL:{0,1}×{0,1}→{0,1},调用IBE方案的密钥生成算法(mskI,mpkI)←KGI(1λ)和伪随机函数密钥生成算法kprf←KGprf(1λ),输出1-ACE方案的主私钥msk=(mskI,kprf)和方案公共参数pp=(mpkI,PL,λ).
2)k←KG(msk,i,t).输入主私钥msk,编号i∈{1,2}和角色t∈{sen,rec,san},密钥生成算法如下:
① 对于输入(msk,1,sen),输出发送者加密密钥ek1=kprf;
② 对于输入(msk,1,rec),输出接收者解密密钥dk1=mskI;
③ 对于输入(msk,2,san),输出信道控制器的重随机化密钥rk=kprf.
3)c←Enc(ek1,m).输入加密密钥ek1和消息m,调用强一次签名密钥生成算法(skS,vkS)←KGS(λ),将vkS作为IBE的身份标识,计算c1=EncI(mpkI,vkI,m)与c2=EncI(mpkI,vkS,Fkprf(c1)),计算签名σ←S(skS,(c1,c2)),输出密文c=(vkS,c1,c2,σ).
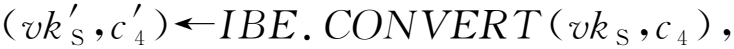

如果同态的IBE方案可以正确解密,则上述方法构造的1-ACE方案同样可以正确解密.
1-ACE方案CCA安全性:记λ为安全参数、PL为通信策略,假设同态IBE方案满足自适应选择身份选择明文攻击下不可区分安全(IND-aID-CPA)和身份变换不可区分性(定义1),一次性签名方案满足选择消息攻击下强存在不可伪造安全性(sEUF-CMA),函数Fkprf(·)满足伪随机安全性.则构造的1-ACE方案满足NR-CCA(PP-CCA与SA-CCA)、NW-CCA与RR-CCA安全性.具体地,对于任意攻击1-ACE方案的敌手A,假设敌手执行qD次解密查询,则存在攻击IBE方案的敌手A′,满足
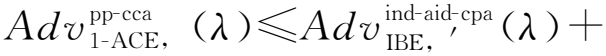
敌手A′的运行时间为T+qD(TE+TD),其中,T为敌手A的运行时间,TE为IBE私钥提取算法的运行时间,TD为执行IBE解密算法的运行时间.
3 方案实例化
CPA安全的访问控制加密方案可以由ElGamal加密、Paillier加密或基于格的同态加密[5,14]结合伪随机函数进行实例化构造.本文重点实例化CCA安全的访问控制加密方案.一种实例化基于带错学习假设(LWE)和最短整数解(SIS)假设,另一种基于判定性双线性Diffie-Hellman(DBDH)假设.通过通用构造方案可知,实例化的核心是构造满足条件的IBE方案,本节只对IBE方案的身份变换算法进行实例化.
3.1 基于LWE与SIS假设方案实例化
CCA安全的访问控制加密方案实例化构造中IBE方案选择文献[13]提出的相关方案,记作GPV-IBE,强一次签名方案同样选择文献[13]的签名方案,在文献[13]中被称为概率性全域哈希方案(probabilistic full hash scheme),结合文献[20]的同态公钥加密设计方法,可以简单地将文献[13]的IBE方案转化为具有同态性质的IBE方案.记GPV-IBE的身份变换算法为GPV-IBE.CONVERT,构造如下.
(id′,c′)←GPV-IBE.CONVERT(id,c):记身份标识映射函数为(id)={ui}i∈{1,…,l},其中ui∈为n维整系数向量,l为明文空间消息长度;GPV-IBE方案的密文拆分为c={(pi,ci)}i∈{1,…,l},其中pi=ATsi+2xi∈包含随机数部分,A∈为主公钥,si∈为随机选取向量,xi←χn为取自误差分布的误差向量;其中ei←χ,mi∈{0,1}为消息比特;随机选取zi←χm,计算输出和

3.2 基于DBDH假设方案实例化
基于DBDH假设的方案实例化主要利用文献[14]提出的IBE方案与文献[21]的强一次签名.记IBE方案为WATERS-IBE,方案的身份变换算法如下.