基于水电储能调节的风光水发电联合优化调度策略

何奇，张宇，邓玲，王海亮，谢琼瑶，王春，胡家旗

(1.国网宜昌供电公司，湖北 宜昌 443000；2.梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北 宜昌 443002)

以新能源为主体的新型电力系统建设是我国“双碳”目标下低碳能源转型的重大战略决策[1-2]。预计到2030年，中国的新能源累计装机容量将超过1 200 GW，超过2020年全球新能源累计装机容量的80%[3]，彼时新能源消纳将面临灵活性调节资源缺口扩大的严峻现实问题。目前，多能互补被视为缓解灵活性资源缺口的有效途径[4]。火电厂可以通过频繁增减出力应对新能源发电的间歇性和不可控性，但频繁的深度调峰会导致过多的煤炭消耗和CO2排放[5]。水电站一直是可靠的低碳灵活资源，具备可控性好、快速调峰等优势[6]。截至2021年底，我国水电装机容量超过390 GW，位于世界各国水电装机总容量的领先地位，其中大多数分布在长江、黄河干流沿线的大型梯级水电站[7]。不少学者在探究水电站与其他多个异质能协同互补优化调度方面取得一定进展：文献[8]考虑风光水互补调度，采用梯级水电进行并网前的风光出力平抑和并网后的负荷跟踪，以追求协同互补系统的最大盈利；文献[9]联合风力发电、光伏发电、水电站以及储氢-燃气轮机系统4种不同发电形式，以各个发电主体利益最大化为目标建立合作博弈模型；针对风电、光伏发电、梯级水电、火电和抽水蓄能电站的混合发电系统，文献[10]以安全水平、经济效益和可再生能源消耗最大为目标，建立多能源电力系统日前联合优化调度模型；文献[11]研究更为贴近实际，结合水电机组检修计划约束，以发电商经济效益最大化为主要优化目标建立模型。然而上述优化调度模型中，梯级水电仍以发电为主，以调节风光新能源波动性和随机性为辅，考虑到未来风光发电预期占比下，风光固有的波动性与不可控性也随之放大，上述模型不再适用于日益扩大的风光装机容量行业前景；因此，部分水电应从常规的发电主体转变为调节者，利用流域梯级水电站群建设梯级互补储能是一种新思路。在上下级水电站之间建设储能泵站，在保证跟踪负荷的情况下，利用储能泵站存储量填平风光新能源余缺，可降低弃风弃光现象的发生，由此，本文提出一种计及新能源消纳与负荷跟踪的风光水储系统短期优化调度策略。

在风光水储的优化调度中，风光出力估计的准确程度影响了优化调度策略的制订[12-13]。现有研究主要使用情景生成和削减方法来模拟可再生能源的短期内出力[14-18]。由于天气条件的间歇性和随机性，风力发电和太阳能发电的功率输出往往带有明显的不确定性。文献[19]基于强化学习、元学习、图神经网络等新兴人工智能技术预测风光出力，文献[20]同时计及数据驱动和物理建模两方面因素；但上述方法均需要大量样本数据作为支撑，且大气数据等物理模型所需数据获取难度较大。考虑到风光出力在更长的时间尺度上具有明显的季节性波动特点，本文提出考虑风光季节性出力不确定和风光耦合功率预测误差的典型场景建立方法，主要内容有：针对风光季节性出力的不确定性，采用季节性自回归移动平均(seasonal auto-regressive lntegrated moving average，SARIMA)预测模型；针对风电-光伏耦合功率输出预测误差，采用Copula理论模型描述，形成基于Copula函数的风光联合概率密度分布函数；搭建考虑负荷跟踪误差、梯级水电站发电量和梯级水电站发电耗水量的多目标优化调度模型；针对模型中的坝上水位-库容、尾水位-下泄流量非线性约束，将其分段线性化后在YALMIP工具箱中调用Gurobi来求解。

1 考虑风光季节性不确定性的概率密度典型场景

根据SARIMA模型可得到风光出力预测值以及误差，再利用Copula函数提取风光预测误差之间的相关信息，得出风光预测误差联合概率密度分布函数。

1.1 SARIMA预测模型

自回归移动平均(auto-regressive lntegrated moving average，ARIMA)模型结合了自回归模型和移动平均模型，在数据拟合优度相近的情况下，可以得到更简单的模型，而且不要求偏自相关函数截尾以及相关函数截尾。以风电出力的预测值xt为例，其公式为

(1-φ1B1-φ2B2-…-φpBp) (1-B1)dxt=

(1+θ1B1+θ2B2+…+θqBq)εt.

(1)

式中：xt为风电出力第t个时间序列(时段t)预测值；φk为k阶自回归模型参数，k=1，2，…，p；θj为j阶移动平均系数，j=1，2，…，q；By为差分算子，作用于xt将其延迟y位(y等于k或j，下文以此类推)，即By=By(xt)=xt-y；d为差分次数；εt为符合正态分布的随机误差。除此之外，在利用SARIMA模型预测数据时，还会对输入预测序列进行差分，以保证预测序列平稳性。

SARIMA模型在ARIMA模型基础上更进一步，引入季节性自回归、季节性差分与季节性移动平均系数。其数学模型为

(1-φ1B1-φ2B2-…-φpBp)×

(1-Φ1Bs-Φ2B2s-…-ΦPBPs)×

(1-B1)d(1-Bs)Dxt=

(1+θ1B1+θ2B2+…+θqBq)×

(1+Θ1Bs+Θ2B2s+…+ΘQBQs)εt.

(2)

式中：Φa为a阶季节性自回归系数，a=1，2，…，P；Θb为b阶季节性移动平均系数，b=1，2，…，Q；D为季节性差分次数；s为季节性周期长度。

1.2 Copula误差修正模型

将历史风光出力数据输入SARIMA预测模型，计算真实值与拟合值之间的误差，将其作为Copula模型的输入。Copula函数表达式为

Ft(τt，ξt)=C(Fw，t(τt)，Fp，t(ξt)).

(3)

式中：Fw，t(τt)、Fp，t(ξt)分别为时段t风电预测误差、光伏预测误差的边缘分布函数，用下标t表示时段t的相关参数，下同；C(·)为Copula连接函数；Ft(τt，ξt)为2个变量的联合分布函数。

常见的Copula函数有5种，包括Gumbel Copula、Clayton Copula、Frank Copula、正态Copula和t-Copula函数。为计及风光处理误差可能存在的负相关关系，本研究选用Frank Copula函数描述风光预测误差之间的关系，对Copula函数进行随机采样生成样本。样本数量较小则不具有代表性，样本数量较多则难以输入后续优化调度模型；因此，对于采用Copula函数生成的场景，本研究在使用拉丁超立方采样后，利用K-means方法进行聚类处理。

(4)

式中：N为样本数量；Tn，t为时段t误差的第n个样本值；h为窗宽；K(·)为核函数。

得到风光预测误差的概率密度函数后，以Frank Copula描述风光预测误差之间的关系，得到两者联合概率密度；接着，对每个时段的联合概率分布函数进行拉丁超立方采样，并根据得到的采样结果计算其对应的边缘分布值；然后，根据该边缘分布值，利用风光的联合概率分布函数反变换，得到每个时段的采样风光预测误差；最后，考虑到生成样本数量众多，通过K-means聚类生成考虑风光相关性和随机性的典型日曲线。其主要步骤如下：

步骤1：将拉丁超立方采样得出[0，1]之间的2个随机数序列αt、βt中的αt，作为风电出力预测误差的边缘分布函数值μt。依据该函数值与Frank Copula函数形式求解式，得出光伏出力预测误差的边缘分布函数值νt，计算式为

(5)

步骤2：由步骤1得出边缘分布函数值μt和νt，然后根据

(6)

得出对应时段t的风、光出力误差τt、ξt。

步骤3：重复上述2个步骤N次，即可得出1日内风光出力预测误差的N种情况，最后利用K-means方法将上述场景聚类为5个风光出力误差代表场景。

以365日、每日96个时段(时长均15 min)的风电预测误差与光伏预测误差作为模型输入，风光误差生成过程如图1。

图1 基于Copula函数的风光误差生成过程Fig.1 Copula function based wind PV error generation

2 风光水储优化调度模型

在梯级水电站之间加装储能泵站结构，如图2所示，加装的泵站可以将下级水电站的水抽至上级水电站，其本质上可以理解为带有抽水蓄能(以下简称“抽蓄”)的梯级水电站。

当出现新能源发电超出所需负荷要求时，储能泵站向上级抽水消耗掉过剩能量，类似储能装置充电；当电网用电需求不能满足时，抽至上级的水量可增加水电站出力，类似储能装置放电。储能泵站改变了常规梯级水电站的水力联系，在上级水电站的水量平衡中增加了来水，而减少了下级水电站的来水。与常规梯级水电站相比，加装储能泵站后既可增加梯级水电站调度灵活性，又可实现水能重复利用。相较于抽蓄电站建设成本高、选址难度大、仅能响应日负荷波动等问题，直接在现有梯级水电站之间进行此项改造既能减少项目投入，也可为平抑季节性波动提供灵活性调节资源。基于此，为提高风光水储系统整体运行效率，优先消纳风光新能源，以负荷跟踪误差最小、梯级水电站发电量最大、梯级水电站发电耗水量最小为目标，考虑风光不确定性场景，构建优化调度模型。

2.1 目标函数

优化调度模型目标函数minW以最小化负荷跟踪误差、最大化梯级水电站发电以及最小化发电用水为目标。

(7)

式中：F1为系统出力与负荷之间的偏差以及储能泵站出力；F2为梯级水电站总出力；F3梯级水电站发电用水量；e为生成的风光出力场景序号；pe为对应场景e的概率；PH，i，t，PL，t与PP，t分别为t时段第i个梯级水电站出力、负荷需求、储能泵站出力，用下标i表示第i个梯级水电站的相关参数，下同；PL，n，t为净负荷(总需求负荷扣除风光出力)；PW，p，t，e、PV，p，t，e分别为场景e下风电预测出力、光伏预测出力；Q，i，t为梯级水电站下泄流量。

2.2 约束条件

约束条件主要由梯级水电站自身运行约束、泵站运行约束以及互斥约束构成。

a) 水量平衡方程式为

Vi，t+1=

(8)

式中：Ii，t为水电站入库径流；Vi，t为水电站库容；QP，t为泵站抽水流量；Qe，i，t、Qd，i，t分别为水电站发电流量、弃水流量；Δt为时段的时长；i=1对应上级水电站，i=2对应下级水电站。

b) 发电性能约束式为：

(9)

式中：Zu，i，t、Zd，i，t分别为水电站坝上水位、尾水位；γ为水电站综合出力系数；fzu、fzd分别为坝上水位-库容关系函数、尾水位-下泄流量关系函数；A为水电转换常数，取9.81。

c) 水位约束式为

Zi，min≤Zu，i，t≤Zi，max.

(10)

式中Zi，t，max、Zi，t，min分别为水电站水位上、下限，用下标max、min相关参数的最大、最小值，下同。

d) 下泄流量约束式为

Qi，min≤Qi，t≤Qi，max.

(11)

e) 机组出力约束式为

PH，i，min≤PH，i，t≤PH，i，max.

(12)

f) 泵站出力约束式为

0≤PP，t≤PP，max.

(13)

g) 泵站流量约束式为

0≤QP，t≤QP，max.

(14)

h) 泵站耗功约束式为

PP，t=Aη(Zu，1，t-Zu，2，t)QP，t.

(15)

式中η为泵站平均效率系数。

i) 互斥约束式为：

(16)

该约束表示储能泵站和梯级水电站在跟踪净负荷时不会同时出力，以避免出现两者出力均较高造成浪费的情况。梯级水电站与储能泵站较一般的双向调节互斥存在区别：若某一时段新能源过剩需要梯级水电站避让发电，且前一时段梯级水电站处于高位运行状态，爬坡能力的约束导致其降低出力后仍难以消纳过剩新能源，在此场景下，储能泵站就应发挥作用；若净负荷小于0，此时需要梯级水电站避免出力，以储能泵站跟踪负荷；若净负荷向下调整，则梯级水电站为避免浪费水力资源也须向下降低出力。

3 模型求解

为缩短模型求解时间，提高模型求解效率，针对梯级水电站坝上水位-库容、尾水位-下泄流量的非线性关系，通过分段将其转化为线性化关系，以避免求解过程中多项式拟合高次项精度与求解效率在一定程度上冲突的问题。根据历史运行资料得出水库日库容变动区间[Vi，min，Vi，max]，将水库库容离散为L个区间，则水位-库容关系式为：

(17)

(Vi，t，l-φi，t，lVc，i，l-1)].

(18)

同理，将水库可行出库流量变动区间[Qi，min，Qi，max]离散为M个区间，尾水位与下泄流量的关系式为：

(19)

(Qi，t，m-ψi，t，mQc，i，m-1)].

(20)

将上述模型线性化后，结合YALMIP建模平台编写程序，在MATLAB 2023中调用Gurobi 10.0求解器求解。

4 算例分析

为验证策略有效性，选取相关的梯级水电站参数，见表1。考虑到时间尺度以年为单位，算例设置为：在夏季与冬季时负荷较高，在春季与秋季时负荷较低，并且在各个典型日夜晚与凌晨负荷较低。风电与光伏装机容量分别为1 200 MW和750 MW；储能泵站共4台泵组，总工作容量为1 000 MW，总最大提水流量为690 m3/s，效率系数η取0.5。

表1 梯级水电站水库参数Tab.1 Reservoir parameters of cascaded hydropower station

4.1 “SARIMA+Copula”风光预测模型

4.1.1 基于SARIMA模型的风光出力预测

对原始风光数据进行平稳性、自相关系数与偏自相关系数校验。进行平稳性检验时，发现风电出力不满足平稳性要求，而光伏出力较为平稳，满足下一步模型拟合数据要求。接着对风电出力数据进行基于损失项的季节项趋势项分解(seasonal-trend decomposition using LOESS，STL)，将其分解为趋势项、季节项和余项后，对趋势项和季节项进行模型拟合，并分别进行拟合后模型残差检验。风电模型拟合结果为：趋势项模型参数为SARIMAX(4，1，5)，季节项模型参数为SARIMAX(5，0，0)。由于计算所得光伏出力较为平稳，故不采用STL方法分解光伏出力原始数据，光伏SARIMA模型拟合结果为SARIMAX(2，1，3)。风电与光伏出力SARIMA模型拟合效果如图3所示。

图3 风电光伏出力数据春季典型日拟合值与实际值对比Fig.3 Comparison of fitted and actual values for a spring typical day of wind PV output data

4.1.2 叠加Copula函数生成的风光出力误差的风光场景

风光出力通常具有明显季节性，因此本研究采用Frank Copula函数拟合出了春夏秋冬4个季节，并对每个季节生成5个风光出力误差代表场景。SARIMA模型因自身缺陷，其预测与实际值往往存在差异。在不同场景下将SARIMA模型的结果叠加上述风光误差之后，可以得到春夏秋冬典型日多场景风光预测出力，如图4、图5所示。在本文所提模型(记为“SARIMA+Coupla模型”)中，对各个场景根据其场景概率进行加权平均计算，可得出1条风光预测曲线，其拟合效果与实际值、SARIMA模型拟合值的对比如图6所示。

图4 春夏秋冬4个季节典型日风电出力代表场景Fig.4 Representative scenarios of typical daily wind power output for four seasons of spring，summer，fall and winter

图5 春夏秋冬4个季节典型日光伏出力代表场景Fig.5 Representative scenarios of typical daily PV output for four seasons of spring，summer，fall and winter

图6 春季典型日SARIMA模型和SARIMA+Coupla模型拟合效果对比Fig.6 Fitting effect comparisons of SARIMA and SARIMA+Coupla models for typical spring days

模型拟合优度由确定系数R2表征，R2越接近1，表示模型拟合越好。其计算方法是用1减去所有样本误差平方和与总平方和的比值，其中总平方和为所有样本均方误差之和。均方根误差(RMSE)是观测值与预测值之差的平方的平均值的平方根，它是衡量预测精度的常用指标，数值越小表示预测越准确。SARIMA模型和SARIMA+Coupla模型的拟合指标对比见表2。

表2 SARIMA模型与SARIMA+Coupla模型拟合指标对比Tab.2 Fitting index comparison of SARIMA model and SARIMA+Coupla model

从表2中可以看出：无论是在风电出力预测还是在光伏出力预测中，SARIMA+Coupla预测模型(有Copula函数生成误差修正)的预测精度要远大于SARIMA模型(不考虑误差修正)的预测精度；SARIMA模型在拟合光伏模型时拟合优度为负值，说明其拟合效果不佳。观察图6也可得出，SARIMA模型拟合结果与实际值存在偏移。

4.2 风光水储优化调度结果分析

将上述预测模型输出数据作为风光水储系统优化调度的边界条件。由于风光出力具有明显季节性，故选取春夏秋冬4个算例，以探究储能泵站的存在对于新能源消纳与负荷跟踪是否有一定效果，此外还探究储能泵站对梯级水电站的水力特性的影响，以及不同目标函数权重下的系统调度结果。

4.2.1 风光水储系统消纳新能源跟踪负荷结果

梯级水电站与储能泵站协同调度可有效消纳新能源并跟踪负荷；但受限于季节性径流、风光出力以及负荷变化等问题，梯级水电站与储能泵站消纳新能源、跟踪负荷的效果随季节差异而不同。

a) 平水期时风光水储系统运行结果

在水库调度的丰、平、枯水期中，春季属于平水期，此时梯级水电站来水量较为均衡，风光水储系统不会出现因来水较多而不得不满发的情况，也不会因缺水而难以发电。

风光水储系统可较好地跟踪春季典型日内每15 min变化的负荷需求。图7、图8展示了春季风光水储系统跟踪负荷以及上下两级水电和储能泵站跟踪净负荷的结果。

图7 春季典型日风光水储系统优化调度结果Fig.7 Optimized scheduling results of wind and water storage systems for typical spring days

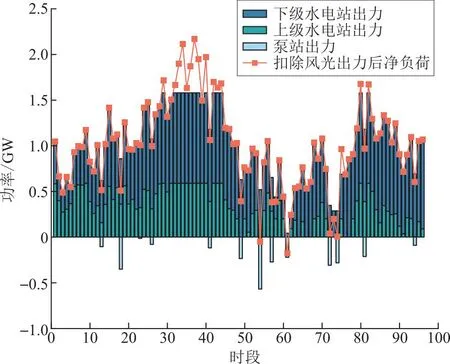
图8 春季梯级水电站及储能泵站跟踪净负荷结果Fig.8 Net load tracking results of cascaded hydropower and storage pump stations in spring

由图7、图8可知，在时段32—时段43中，总负荷与净负荷超出风光水最大出力，系统难以达到跟踪负荷要求。储能泵站负责在净负荷下调时，以消耗电能的方式提供额外下调功率，然而梯级水电站和储能泵站的协调调度较常规储能装置更为复杂。在净负荷下调时，应当优先由梯级水电站降低出力提供下调裕度跟踪负荷；但梯级水电站下调功率受到约束，此时即需要储能泵站出力消纳掉过剩的水电站出力，实际上在净负荷为正但负荷变动为负的情况下，梯级水电站与储能泵站不可避免出现同时工作现象。因两者的优先级不同，若两者同时调度，则可能出现：梯级水电站下调功率裕度不足，仍维持在高位发电；储能泵站为跟踪下调负荷不得不同样维持较高出力。此时梯级水电站出力与净负荷叠加上储能泵站出力维持在高位平衡，造成水力资源和电能浪费。由图8可知，储能泵站出力往往伴随着净负荷在该时段较前一时段下调，但这并不代表梯级水电站下调功率裕度用尽。如在时段18，此时净负荷较前一时段下调近620 MW，但梯级水电站较前一时段下调270 MW，泵站出力350 MW以弥补下调功率缺额。梯级水电站之所以未用尽下调功率裕度，是与后一时段有关，后一时段净负荷较该时段上涨750 MW。计及下一时段上调需求与裕度，梯级水电站此时并未过多降低出力。

秋季情况较春季有相似之处，区别在于风光出力情况较春季有较大变化，导致净负荷情况较春季有所区别。图9、图10展示了秋季风光水储系统跟踪负荷以及上下两级水电和储能泵站跟踪净负荷的结果。

图9 秋季典型日风光水储系统优化调度结果Fig.9 Optimized scheduling results of wind and water storage systems for typical days in autumn

图10 秋季梯级水电站及储能泵站跟踪净负荷结果Fig.10 Net load tracking results of cascaded hydropower and storage pump stations in autumn

由图9、图10可知，在时段53—时段72内，风光出力大增且呈现显著波动性，造成净负荷在该范围内呈正负值反复波动，呈现出前一时段为正、后一时段为负的特点。在净负荷为正时，由水电站出力跟踪负荷；净负荷为负时，则将水电站出力降低至0。未出现春季梯级水电站出力未充分下调的原因，在于此季节净负荷尽管在正负值间波动，但并未超出梯级水电站爬坡功率上下限。

b) 丰水期时风光水储系统运行结果

在夏季，梯级水电站来水较多，可将其视为调节裕度较小的电源，且负荷峰谷差较春季时更大，前后时段负荷变化幅度也更大。此时梯级水电站以及泵站跟踪负荷较平水期效果相对较差。图11、图12展示了夏季风光水储系统跟踪负荷以及上下两级水电和储能泵站跟踪净负荷的结果。

图11 夏季典型日风光水储系统优化调度结果Fig.11 Optimized scheduling results of wind and water storage systems for typical summer days

图12 夏季梯级水电站及储能泵站跟踪净负荷结果Fig.12 Net load tracking results of cascaded hydropower and storage pump stations in summer

由图11、图12可知，在前3个时段内负荷剧烈上下波动，且波动范围显著超出了梯级水电站的调节裕度。为兼顾3个时段的跟踪误差之和最小，梯级水电站在时段1以及时段3的出力均仅有400 MW，在时段2则降低至0，由储能泵站负责跟踪净负荷。该情况同样发生在时段13前后、时段39前后，以及时段70附近。尽管夏季负荷峰值较高，但此时的风光出力也同样较大，一定程度上削弱了净负荷较平水期的变动。

c) 枯水期时风光水储系统运行结果

冬季为梯级水电站优化调度枯水期，此时风光出力较平水期和丰水期偏少。图13、图14展示了冬季风光水储系统跟踪负荷以及上下两级水电和储能泵站跟踪净负荷的结果。

图13 冬季典型日风光水储系统优化调度结果Fig.13 Optimized scheduling results of wind and water storage systems for typical winter days

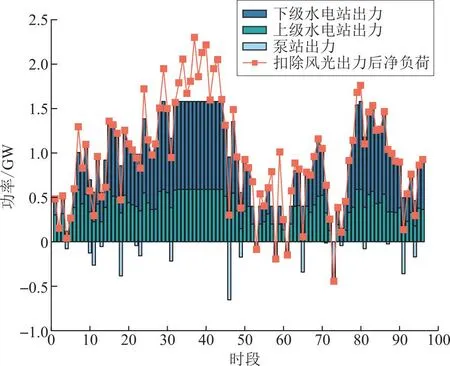
图14 冬季梯级水电站及储能泵站跟踪净负荷结果Fig.14 Net load tracking results of cascaded hydropower and storage pump stations in winter

由图13、图14可知，冬季枯水期净负荷仅在4个时段为负，较少出现净负荷峰谷差较大、在正负范围内剧烈波动的情况，以及像丰水期和平水期频繁出现的、为考虑前后净负荷正负而将功率锁定在爬坡阈值的情况。

d) 弃风弃光结果分析

为验证所提模型的有效性与实用性，以式(7)—式(20)为模型，建立不含储能电站的风光水系统。此时由于不存在储能，故目标函数更改为：

(21)

水量平衡方程式较式(8)也有变化，将其修改为：

(22)

表3展示了有无储能泵站下系统优化调度各项指标结果。

表3 有储能泵站与无储能泵站对比Tab.3 Comparison of pumping stations with and without energy storage MWh

由表3可知：较常规风光水系统，风光水储系统可以有效减少弃风弃光，在保证跟踪负荷的前提下最大程度促进新能源消纳；风光水储系统可将过剩新能源的50%转化为上级电站水能量进行储存。减少弃电量呈现出明显季节特点：①夏季因负荷与风光出力均位于高位，面临的问题是兼顾追踪正负波动的净负荷，导致向上调节(增加水电站和泵站的总出力)时不能很好跟踪负荷；但消纳新能源、向下调节(降低水电站和泵站的总出力)时仍然有较大裕度，因此其弃电量较少。②冬季位于枯水期，相较于夏季，冬季枯水期水位压力较小，向下调节时无需顾及水位过高带来的影响，同时泵站也可参与出力重复利用水能。考虑到此时净负荷大多位于正区间，储能泵站较其他季节无需单独负担向下调节任务。③春节和秋季均属于平水期，此时来水量适中，梯级水电站出力和储能泵站耗功主要受风光出力与负荷变化影响。如前文所述，秋季因净负荷变化多位于梯级水电站调节裕度之间，较春季消纳新能源裕度更为充裕，因此消纳风光发电量较多。

4.2.2 泵站对梯级水电站调度上下库容和水头的影响

从理论分析来看，在水电站库容以及水位调度仍有较大裕度的情况下，在上下级水电站之间加装泵站有利于重复利用水能，减少弃水。以春季平水期为例，对比加装储能泵站与否时上下级水电站库容以及发电水头。

图15、图16展示了有无储能泵站时两级水电站的库容以及水头变化情况。

图15 有无储能时上级电站库容以及发电水头对比Fig.15 Comparison of parent station's storage capacity and the generation head with and without energy storage

图16 有无储能时下级电站库容以及发电水头对比Fig.16 Comparison of subordinate station's storage capacity and the generation head with and without energy storage

(图15、16左侧纵轴标目单位不删括号，括号前加斜线)

由图15、图16可知，储能泵站的存在显著改变了上下水库的库容以及发电水头。对上级水电站来说，其库容下降明显较未加装储能泵站时慢，这是因为泵站利用过剩的新能源将上级电站下泄用水抽至上级水库；但上级电站的水头受此影响有所下降。对下级电站来说，由于泵站抽水作用，其库容下降较未加装泵站时快；但因上级水位下降较慢，其发电水头较未加装泵站时有明显增长。

4.2.3 不同目标函数权重下优化调度结果

原优化调度模型中的3个目标函数(F1、F2、F3)权重一样。在实际生产调度过程中，受限于不同流域来水量不同、不同地区风光装机容量不一致、梯级水电站自身调峰调频任务较重等因素，系统多目标优化调度必然存在优先级。以下以春季平水期为例，探究不同目标函数权重下风光水储系统优化调度结果。当侧重净负荷跟踪时，F1、F2、F3的权重依次为0.7、0.15、0.15；当侧重梯级水电站出力时，F1、F2、F3的权重依次为0.15、0.7、0.15；当侧重耗水量时，F1、F2、F3的权重依次为0.15、0.15、0.7。从理论上看：若无储能泵站，梯级水电站发电用水最小化与发电最大化是有冲突的，储能泵站通过重复利用水能缓解这一矛盾；但为多消纳新能源而驱使储能泵站过多用能，则会影响负荷跟踪效果。

不同目标函数权重下风光水储系统优化调度结果主要指标数据见表4，可知目标函数权重不同，优化调度结果存在显著差异性。图17、图18以及图19分别展示了风光水储系统侧重跟踪负荷、水电站发电量以及耗水量时的优化调度结果。

表4 不同目标函数权重下负荷跟踪误差、发电量及泵站总消耗电量Tab.4 Load tracking error，power generation and power consumption data of pumping stations under different objective function weights MWh

图17 目标函数权重为0.7、0.15、0.15时优化调度结果Fig.17 Optimized scheduling results with objective function weights of 0.7，0.15，0.15

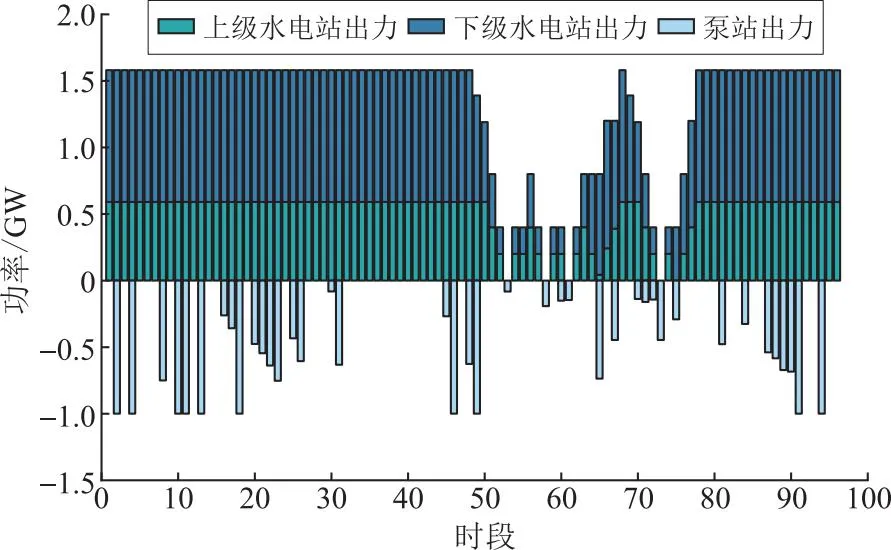
图18 目标函数权重为0.15、0.7、0.15时优化调度结果Fig.18 Optimized scheduling results with objective function weights of 0.15，0.7，0.15

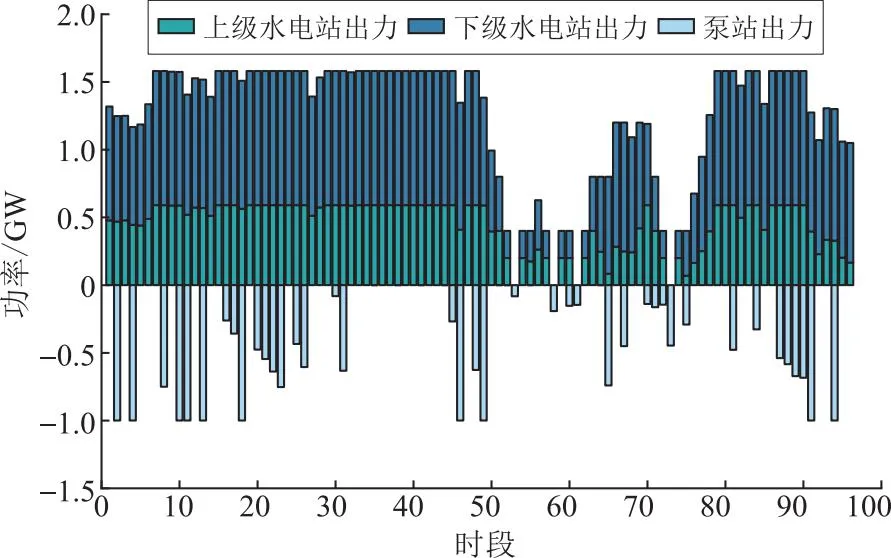
图19 目标函数权重为0.15、0.15、0.7时优化调度结果Fig.19 Optimized scheduling results with objective function weights of 0.15，0.15，0.7

由图17可知，当以跟踪负荷为主要目标时：负荷跟踪误差最小；相较于其他2种方案，此时梯级水电站存在避让新能源发电现象，故水电站发电量最小。由图18可知，当以梯级水电站发电量最大为主要目标时：水电站在1日96个调度时段满发；考虑到新能源发电的叠加作用，此时负荷跟踪效果较差，但总发电量最大。由图19可知，当以用水量最小为主要目标时：一方面梯级水电站收缩发电量减少用水；另一方面储能泵站尽可能重复利用水能，储能泵站出力最大。

5 结论

本文所提出的风光水储协同运行优化调度策略，可以有效减少风光新能源运行时面临的弃风弃光问题。算例分析表明：

a)SARIMA预测模型和Copula函数误差修正模型可以为风光水储在日内的超短期风光预测提供较为准确的依据。

b)风光水储系统在丰、平、枯水期均可以起到负荷跟踪以及促进新能源消纳的效果，枯水期的风光水储系统在减少弃风弃光方面达到最优。尽管风光水储系统在汛期的效果较丰水期和平水期效果不佳，但仍然优于不加装储能泵站。

c)相较于未加装储能泵站，加装储能泵站后：上级电站的水头有所下降，但库容下降较慢；下级水库水头上升，但库容变化较快。

d)目标函数的不同权重也将显著影响优化调度结果，风光水储系统可根据来水量、负荷以及风光出力情况，合理选择目标权重以实现系统最优调度。