基于改进FCM聚类的光伏电站出力场景特性研究

苗璐，樊玮，肖红燕，刘宇，陈德扬，张勇军

(1. 广东电网有限责任公司电力调度控制中心，广东 广州 510220；2. 智慧能源工程技术研究中心，华南理工大学 电力学院，广东 广州 510640)

“双碳”目标的提出，加快了我国新能源发电建设和能源转型的步伐。2023年我国光伏电站装机容量已经突破5亿kW，其波动性和间歇性给电网安全可靠性带来了巨大挑战[1-3]，为此，研究光伏发电的出力特性受到广泛关注[4-6]。文献[4]对光伏出力的季/日特性及概率分布曲线进行分析，得出不同区域间的出力相关性；文献[5]从时间和频率角度分析光伏出力的波动性，得出在不同天气下光伏出力的特性；文献[6]利用运行监测数据总结了光伏电站的运行特性。

由于光伏发电出力的不确定性和波动性大，在研究光伏并网的机理和对策时面临场景多、数据多、计算复杂度高的难题。因此，简化光伏出力场景、优化分析方法十分必要[7-11]。对场景优化的方法常见场景缩减法[7，9]和时序模拟法[12]等，其中场景缩减法应用较为广泛。场景缩减法多与聚类算法相结合[7]，通过将数据中的相似数据归为一类、相异数据划分开，来生成多个类别的场景集。目前聚类算法主要有K-means聚类、学习向量化聚类和K-近邻算法等。其中K-means算法是目前应用最广泛的聚类算法，但初始聚类中心和聚类数目是随机确定的，易导致聚类结果收敛性不足，陷入局部最优解。

为此，文献[7]采用K-means聚类并基于密度思想和距离最大、最小原则来确定聚类中心，文献[13]提出聚类有效性指标来提高收敛性。与K-means类似的模糊C均值(fuzzy C-means，FCM)聚类算法，引入隶属度函数来分析不同样本间的相似程度，得出样本属于不同类别的权重，提高了聚类灵活性[6-7]，但也存在初始聚类中心与最优聚类数目不确定的问题。针对此：文献[8]提出用皮尔逊相关系数代替传统欧氏距离，来确定聚类中心；文献[14]采用聚类有效性指标CH来确定最优聚类数目，改进传统FCM算法；文献[15]将粒子群优化算法与FCM聚类算法相结合，确定初始聚类中心与最优聚类数目。面对波动性大、场景多的新能源发电，如何优化聚类后的场景缩减成为关键问题。针对该问题：文献[7]结合K-means算法与同步回代消除算法(simultaneous backward reduction，SBR)进行场景缩减；文献[8]用后向场景削减方法确定典型场景；文献[9]提出粒子群和遗传优化算法与聚类相结合的场景缩减法；文献[16]采用Wasserstein概率距离来处理光伏和风电数据，并基于改进K-medoids算法生成场景。

总的来看，现有文献采用FCM算法分析光伏出力时，没有同时考虑初始聚类中心选取、聚类数目确定和最终典型场景形成与缩减等情况，导致最终聚类结果收敛性不足，以及某类中存在较多场景，增加了分析难度。据此，本文首先建立光伏出力特性的评价指标，进而提出一种改进FCM聚类算法，确定初始聚类中心与聚类数目，再基于概率距离采用场景缩减法对聚类后的场景进行缩减，得到具有典型特征的光伏出力场景，降低传统分析出力数据的复杂性，为后续研究光伏出力特性奠定基础。最后以广东省某200 MW光伏电站为例进行仿真验证。

1 光伏出力特性评价指标

光伏出力的波动性和不确定性，使得对大量光伏数据进行分析存在困难，而采用聚类算法划分出力特性时，数据较多也会增加复杂度，并降低运算速度；因此须先采用评价指标量化表征出力特性，对数据进行降维处理。为此本文考虑2个一级指标(波动性和出力效率)，并针对2个一级指标，设定多个二级指标用以更具体地分析不同属性。用这些指标表示1日内的出力特性，可降低聚类分析维度。

1.1 一级指标选用思路

光伏发电作为一种新能源发电，受自然环境的影响较大，其中主要受到光照影响。光照具有不确定性，会在不同时刻形成出力波动，很有必要分析这些波动情况，以更进一步掌握光伏电站的并网对系统是否造成影响以及影响程度大小。利用波动性指标评估系统的波动情况，可得出光伏出力对系统的影响程度。此外，光伏发电效率也一直是备受关心的问题，对光伏出力效率进行研究，也可以更好地评估光伏电站的出力特性。

为此，将波动性和效率作为一级指标，从整体上衡量光伏出力特性，波动性越小，效率越高，表示该时刻的出力水平越高。其中针对波动性又设定3个二级指标，分别为变异系数α[16]、极端波动率Kpfr[10]和平均波动系数Kfluc[10]。出力效率设定有效出力率η、平均出力水平Paver和发电时间比β这3个二级指标。

1.2 波动性分析

光伏发电本身是一个多变量的非线性问题，其受到光照、温度、光伏板面积等多种因素影响，且出力数据存在一定的波动性，这种波动造成发出的有功功率增减，危害系统稳定，所以需要对波动性进行分析。

1.2.1 变异系数

分析某段时间的光伏出力，用标准差σ来表示该时段整体出力偏离平均出力的情况，用平均值u表示该时段内整体出力水平。但仅用这2个评估指标还不能较精确地体现出力波动情况，将两者结合，则可以得到变异系数

α=σ/u.

(1)

变异系数越大，表示数据偏离平均值越大，波动性越大，这是用来衡量数据波动程度的一个典型指标，将其作为波动性的二级指标具有较好的适应性。

1.2.2 极端波动率

该指标表示光伏整体出力中超过或低于极限波动变化率的时刻数占1日内总时刻的比例，其中波动变化率是指在一小段时间内对光伏出力求差分，表示该小段时间内光伏出力的变化量。极端波动率

(2)

(3)

式中：v为波动变化率，vmax和vmin分别表示最大和最小波动变化率；t为周期内的时刻，T为周期内总时刻数。Kpfr可以衡量一段时间内波动的越限次数，从而分析该时段是否存在较剧烈的波动情况。

1.2.3 平均波动系数

该指标用来衡量研究周期内的波动反转次数，其计算式如下：

(4)

(5)

式中Pt、Pt-1和Pt+1分别为时刻t、t-1和t+1的有功出力值。(Pt-Pt-1)(Pt-Pt+1)>0时表示出力反向1次，即存在波动，但具体波动大小，则需参考指标极端波动率和变异系数。

1.3 出力效率分析

出力效率即衡量光伏电站在一定时间内的出力效果，本文采用3个二级指标来衡量光伏发电效率。

1.3.1 有效出力率

有效出力率指在研究周期内光伏出力大于0的各时刻功率平均值与电站装机容量之比，利用该指标可以评估不同季节光伏电站发电效率和运行状况，其定义为

(6)

式中：TL为周期内有效出力(光伏出力大于0)时间长度对应的时刻数；S为电站装机容量。通常，η越大表示光伏电站发电状况越好，光伏发电效率越高。

1.3.2 平均出力水平

平均出力水平Paver为在研究周期内各时刻光伏发电出力的平均值，代表在此周期内的出力整体水平，Paver越大，表示该时段内的出力效率越高，表示为

(7)

1.3.3 发电时间比

发电时间比β定义为周期内有效出力时刻数度占周期总时刻数的比例，β越大，表示研究周期内的出力效率越高。

β=TL/T.

(8)

1.4 小结

本文结合上述6个光伏出力特性指标来评估某日的出力特性，即用指标表征1日内的出力特征，将1个时间多维度问题转化为六维问题，构成以下特征数组：

X=(α，Kpfr，Kfluc，η，Paver，β).

(9)

由此，大大降低了数据分析的维度，有利于后续聚类分析。

2 FCM聚类方法改进与场景缩减

K-means算法用于聚类时，直接将样本划分到欧式距离最近的类簇中去，得到的聚类结果缺乏灵活性，且没有考虑与其他类的关系。鉴于此，本文采用改进的FCM聚类算法对样本数据进行聚类，弥补初始聚类中心随机选取和最优聚类数目不确定的缺陷。同时，考虑到聚类后场景较多的情况，分析数据特性较复杂，提出基于概率距离的思想对场景进行缩减，得到具有典型特征的场景用以表示该类情况，简化了分析过程。

2.1 初始聚类中心选取

传统FCM算法与传统K-means算法的不同在于FCM算法引入了隶属度函数(即表示样本属于不同类的权重)，避免了K-means算法直接将样本划分为类别的硬性，即样本只属于某一类，不具有权重代表。

利用第1章形成的六维指标数组，给定N个样本，形成N×6的特征矩阵x。假设将样本数据划分为c类，那么将得到c个聚类中心，其中第j个样本属于第l类的概率即为隶属度ulj，每个样本的隶属度总和为1。FCM算法的目标为各类样本到聚类中心的距离之和最小，因此得到目标函数J和隶属度函数约束[7]如下：

(10)

(11)

式(10)中：m为隶属度因子；Xj为第j个样本根据第1章的指标形成的特征数组，它是矩阵x中某一行的数据；Cl为第l个聚类中心的特征数组。通过求解目标函数可得隶属度函数和聚类中心，即：

(12)

(13)

式(12)中Ck为第k个聚类中心的特征数组。

本文对聚类中心选取进行改进，基于密度思想和距离最大、最小原则得到初始聚类中心，进而得到全局最优解。改进后的目标函数

(14)

(15)

得到聚类中心

(16)

式(14)、(16)中Xg为第g个样本的特征数组。

求取初始聚类中心的步骤如下。

步骤1：计算各样本数据间的欧式距离并进行排序，选择距离最近的2个样本作为初始样本，并将2个样本的均值作为第1个初始聚类中心。

(17)

式中dgj为任意样本g与样本j之间的欧氏距离。

步骤2：剔除步骤1中2个初始样本g和j，保留距离这2个初始样本较大距离的样本，剩余样本集形成新的样本集，同样求取欧式距离并进行排序，选择距离最近的作为第2个初始样本对，并求均值得到1个特征数组，取其为聚类中心，不断迭代，得到各聚类中心。

M=sort ‖Xw-Xe‖，w，e≠g，j；w，e∈N.

(18)

式中：M为新样本集构成的距离排序矩阵；Xw和Xe分别为第w和e个样本的特征数组。其中sort表示将样本集的欧式距离进行从小到大排序。

步骤3：若剩余样本集只含有2个样本，则取其平均值为最后1个聚类中心，2个样本数据构成样本集，最终形成初始聚类中心集。

密度思想和最大、最小初始中心选取原则综合考虑了各样本数据间的距离，通过不断迭代计算，得到具有代表性的聚类中心，后一聚类中心的形成不仅只依赖于前一聚类中心，避免了K-means算法中只计算样本与各聚类中心距离从而形成新的样本集的局限性。

2.2 基于手肘法和CH指标的最优聚类数目确定

适当的聚类数目是得到最优聚类结果的关键。聚类数目较多时，聚类结果较精确，类内关系更紧致，但结果较复杂；聚类数目较少时，得到的聚类结果存在一定误差。因此合理选择聚类中心十分重要。

根据聚类算法的有效指标，确定最优聚类数目。采用手肘法中的聚类误差平方和(sum of squares of error in cluster，SSE)指标和CH指标相结合的方式[8-10]计算各样本离该类聚类中心的误差平方和。SSE指标(SSSE)的表达式为

(19)

式中：cl为聚类中心下所有的样本；Xjl为属于第l类的第j个样本的特征数组。SSSE随着聚类数目的增多而逐渐减小，当每个样本构成1类时，聚类结果最精确，但结果较复杂，而聚类数目过少，则聚类结果不精确；因此选择SSSE下降最快的点对应的聚类数来表示最优聚类数目。

CH指标(SCH)用于计算类间距离与类内距离的比值，其计算如下：

(20)

式(20)中分母表示类内距离差方和，其越小越好；分子表示类间距离差方和，SCH越大越好。因此，应选择较大的SCH对应的聚类数目。

本文结合SSSE和SCH，得到最佳聚类数目，避免了单一指标的局限性，寻找最优聚类数目可以转化为求取SSSE下降最快的点与SCH较大的点相结合的点，从而综合分析得到最优值。

2.3 场景缩减

样本聚类得到多个类别的场景集，若样本数N足够多，将导致类中的数据集较多而无法显现该周期内光伏出力的典型特征。因此利用概率距离[7]比较方法对聚类后的场景进行缩减，保留每类中具有代表性的样本。

首先计算每类中样本间的欧式距离，得到距离矩阵

Dgj=‖Xg-Xj‖，g≠j；

(21)

式(21)表示求取各个样本间的欧式距离公式，对矩阵D赋予下标表示某2个样本间的距离。

计算各样本的概率距离，并选择与剩余样本概率距离最近的样本s1，在距离矩阵D中找到与s1距离最小的样本s2代替s1，其余样本构成剩余样本集，并求取新的距离矩阵。不断迭代，直到保留到所需场景数，即得到典型场景，由此完成场景缩减。其中概率距离

δg=pgl‖Xg-Xj‖.

(22)

式中pgl为第g个样本属于第l类的概率，用样本的等概率分布表示。

2.4 聚类步骤

综上分析，改进后的FCM算法具有较好的全局搜索性和精确性，结果较精简，相比于传统FCM算法，其多了3个步骤。具体改进后的步骤如下：

步骤1：对1年的光伏出力数据进行预处理，求出每日的特性指标代替原始实际出力值，表征出力的波动和周期性等。

步骤2：求取样本集中各样本的欧式距离，构成初始距离矩阵，并根据密度思想和距离最大、最小原则得到初始聚类中心。

步骤3：依据步骤1得到的初始聚类中心，根据样本间的欧式距离矩阵不断迭代，更新隶属度矩阵和聚类中心，直到目标函数达到精度或聚类中心不变化，则停止迭代，得到最终聚类结果。

步骤4：根据不同聚类数目，以SSE指标和CH指标衡量最终结果，得到最优聚类数目。

步骤5：根据最后的聚类结果削减不同类的场景数，得到具有代表性的典型场景。

整个聚类分析过程(包含场景缩减流程)如图1所示。图1中，k为聚类数目，p为迭代次数，季度+1表示对1年中4个季度的光伏特性轮流分析。

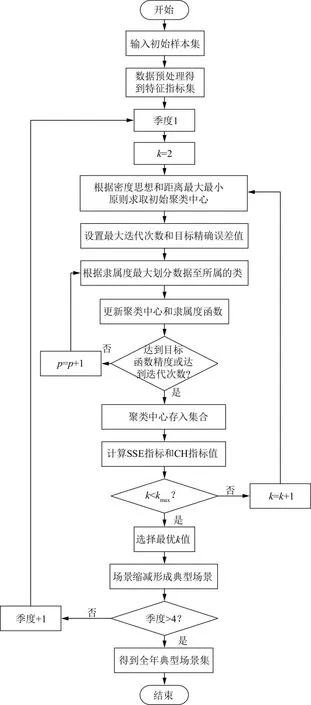
图1 聚类流程Fig.1 Clustering flowchart

3 仿真与验证

本文基于MATLAB 2016b运行环境，利用南方某200 MW装机的光伏电站2022年7月—2023年6月的数据进行仿真，采样间隔为10 min。用上文所述的方法对原始数据进行处理，并将1年的数据划分为4个季度进行分析，最终聚类完成后得到4个具有代表性的典型季出力场景。

3.1 数据处理

1年中的出力数据以10 min为间隔进行处理，1日的数据处理量为144个。若将144组数据做聚类处理，当天数较少时过程简便，而天数增多时，聚类过程较复杂。本文将光伏实际处理曲线转化为第1章节所述6个代表性指标，用以表征1日内的出力特性。以1年4个季度为区间，得到各季度的指标特性。表1—表4为各季度部分日归一化后的指标特征。

表1 春季特征指标Tab.1 Spring characteristic indicators

表2 夏季特征指标Tab.2 Summer characteristic indicators

表3 秋季特征指标Tab.3 Autumn characteristic indicators

表4 冬季特征指标Tab.4 Winter characteristic indicators

由表1—表4可知不同季度在波动性和出力效率方面存在差异性，但数据繁多，对每日的数据进行分析较为复杂，因此采用聚类对数据进行划分，进而缩减场景得到典型场景集，该方法优化了分析过程，并得到了较为准确的结果。

3.2 聚类分析

将各个季度的六维数据分别进行聚类分析，求取初始聚类中心，得到不同聚类数目下的聚类结果。本文结合SSE指标和CH指标进行评估，当聚类数目达到某一值时，2个指标的综合取值最优，则这个点为最优聚类数目点。图2所示为不同季节的聚类有效性指标。

图2 不同季节聚类有效性指标Fig.2 Clustering efficiency indicators in different seasons

由图2可知：春季SSSE在k=4时下降最快，而在k=5后下降速度逐渐缓慢，此时SCH达到最大值，综合得最优聚类数为5；夏季k=3时，SSSE下降速度最快，同时SCH达到较大值，该季节的最优聚类数目为3；秋季k=4时，SCH达到最大值，而SSSE在聚类数目超过4后缓慢减少，因此选取最优聚类数目为4；冬季k=3时，2个指标取值最优，因此该季节的最优聚类数目为3。

根据以上得出的各季度的最优聚类数目，分别进行聚类分析得到聚类结果。最终的聚类中心和聚类集见表5。

表5 聚类后各聚类中心Tab.5 Cluster centers after clustering

春季第1类包含22日的数据，第2类包含21日的数据，第3类包含24日的数据，第4类包含9日的数据，第5类包含14日的数据。

夏季第1类包含31日的数据，第2类包含30日的数据，第3类包含31日的数据，每类出力数据存在差异，代表1个季度的3种出力特征。

秋季第1类包含27日的数据，第2类包含23日的数据，第3类包含19日的数据，第4类包含23日的数据。

冬季第1类包含27日的数据，第2类包含35日的数据，第3类包含25日的数据。

3.3 场景缩减

聚类完成后，每个季度都具有几个代表性特征的类，但每类中的样本数据太多，对于分析光伏出力特性不利，因此本文提出场景削减方法。以概率距离为基础不断删除原类别中的场景，保留最终具有代表性的某个场景，得到最终四季典型出力场景特征值的数据结果，见表6。

表6 典型出力场景特征值Tab.6 Characteristic values of typical output scenarios

根据聚类得出典型场景的指标值，以及求出的实际出力值，绘制出场景如图3所示。

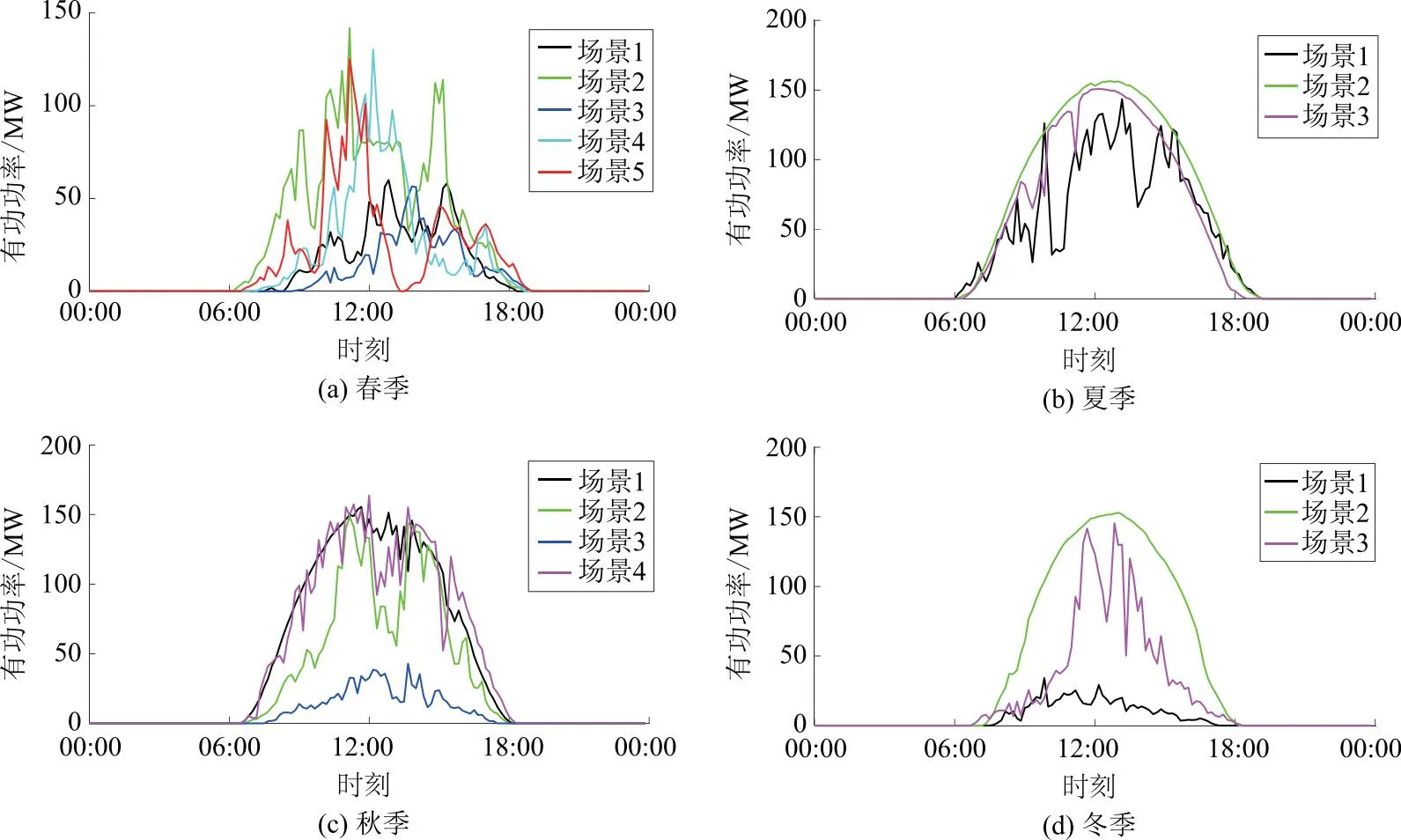
图3 典型场景Fig.3 Typical scenarios

根据图3得到不同季节的典型出力场景，其中每个场景用具有代表性的1组出力数据表示。与传统聚类结果用多组数据表示相比，本文场景缩减后分析更明确简洁。分析该光伏电站冬季场景1与其他2个场景的出力曲线可知该季节出力较不均匀，偏差较大，出力波动性较春季更平缓。

3.4 改进FCM算法验证

采用传统K-means算法、原始FCM算法对同一组数据进行聚类分析，验证本文改进FCM聚类算法的优越性。以聚类有效性指标SSSE和SCH相结合为评估参数，得到聚类结果见表7。

表7 不同聚类算法对比结果Tab.7 Comparisons of different clustering algorithms

由表7可见，改进FCM算法在各个季节聚类结果均优于其他2种算法，尤其是在秋季，聚类优越性较为显著。

对比传统FCM算法与本文算法的SSSE，确定初始聚类中心与聚类数目在一定程度上提高了聚类的精度与收敛性。对比传统K-means算法，由于FCM算法引入了隶属度函数，使样本不局限于只属于某一类，而是属于每类，只是权重不一样，这也提高了算法的精确性。

验证本文聚类完成后场景缩减的优越性，将其他2种算法的聚类结果绘制成图4、5。

图4 传统FCM算法聚类结果Fig.4 Clustering results of traditional FCM algorithm

由图4、图5可见，传统FCM和K-means算法的聚类结果较为复杂，数据未经处理，且出力特性分析也增加了工作量，由此更进一步证明了采用本文算法缩减场景的必要性。对比图3、图4和图5，本文采用场景缩减最终得到的典型场景清晰显示了该时段的光伏出力情况，简化了聚类结果。

图5 传统K-means聚类结果Fig.5 Clustering results of traditional K-means

4 结论

针对传统FCM算法的不足，本文结合密度思想和距离最大、最小原则优化初始聚类中心选取，并采用聚类有效性指标评估得到的最优聚类数目，提高了聚类的精确性和简洁性，并加快了运算速度。考虑到分析光伏出力数据的繁琐，采用基于概率距离的场景缩减法得到典型场景，进而更好地分析不同季度的出力特性。得出以下结论：

a)采用出力特性指标代替实际出力值，可以简化分析过程，降低聚类维度，提高运算速度。

b)本文对初始聚类中心的选取和最优聚类数目的确定，在一定程度上避免了达到聚类局部最优，优化了聚类结果。

采用场景缩减法得到具有典型特征的场景，并通过广东省某一光伏电站的实际数据验证，得到该电站不同季度的典型出力场景，优化了光伏出力特性分析过程，证明了该方法的实用性。