融合多尺度特征卷积神经网络的多光谱图像压缩方法

张丽丽，陈子坤，潘天鹏，屈乐乐

（沈阳航空航天大学 电子信息工程学院，辽宁 沈阳 110136）

1 引言

多光谱图像在空间和光谱维度上具有高分辨率的特点，在军事、农业检测和测绘等多个领域有着广泛的应用［1-4］。但由于多光谱图像数据具有维度高，数据量大的特点，存在着存储和传输的问题［5-7］。普通图像每个像素的数据大小为8 bit，而多光谱图像每个像素的数据大小为16 bit，所以在图像大小相同的情况下，多光谱图像有着比普通图像更高的数据量。所以对多光谱图像在高比特率下进行高效的压缩和重建方法的研究是很有必要的。

应用于多光谱图像压缩的传统图像压缩方法一般有JPEG2000［8］和3D-SPIHT［9］等，这些方法既能实现码率可变的图像压缩又可以实现高压缩比的有损压缩［10］，支持区域感兴趣编码，能够选择性地对特定区域进行压缩和解压缩。但是以上算法都存在着复杂度高，重建图像质量不高的问题。因此，传统图像压缩方法已经不能满足高效多光谱图像压缩的要求。

近年来，深度学习有损图像压缩方法得到了迅速发展。相对于传统图像压缩算法，深度学习算法对图像的特征提取、表达能力以及对高维数据的处理能力等方面有着很大的优势。同时深度学习方法可以进行端到端的学习和优化［11］，从原始图像到压缩编码的整个过程都可以通过神经网络进行端到端训练。这样可以更好地统一优化压缩和解压缩过程，提高整体性能。

卷积神经网络（Convolutional Neural Networks,CNN）［12］因其优异的局部感知能力、多层次特征提取能力在深度学习图像压缩当中得到了大量的应用。传统基于CNN 的图像压缩模型结构为：编码器，解码器，量化器以及熵编解码器。其中编码器，解码器由CNN 构成。为进一步获得更优的压缩效果，Ballé 等人提出了超先验的概念［13］，指出应该为潜在表示下的每个像素点分别估计各自的分布、均值和方差，在熵编码阶段中依据该信息，可以有效地消除原潜在表示中存在的边信息，得到消除空间冗余后的潜在表示，可以得到更优的熵编码。此外，其在编解码网络中加入广义除法归一化（Normalization of (Inverse)Generalized Division,GDN/IGDN）提高网络的潜在特征提取能力。Minnen 等人在Ballé 等人的模型基础上做了改进［14］。在保留核心自编码器网络和超先验网络的结构下，添加了基于自回归的上下文模型。编码器网络学习图像量化后的潜在表示，上下文模型通过自回归预测熵模型的概率分布，而超先验网络学习图像的隐藏特征的表示信息，用于修正和调整上下文模型的预测结果。

对于多光谱图像，以上提出的模型其结构并不能高效地提取到多光谱图像的光谱间特征。为了能提取到空间特征和谱间特征，Kong 等人在2020 年提出了一种基于加权特征通道残差网络的端到端多光谱图像压缩框架［15］，通过残差块统一去除多光谱图像中的冗余信息，但其并没有单独针对光谱间和空间信息进行处理，之后kong等人提出了一种空间光谱间双路特征提取网络［16］，将空间和光谱特征分别提取并融合，并对空间特征的提取采用组卷积的方式避免与光谱间特征发生混淆。在2020 年，Roy 等人提出了一种混合频谱CNN［17］，它由3DCNN 和2DCNN 组成，先使用3DCNN 来提取联合光谱空间特征，再使用2DCNN 来学习更抽象的空间表示。在2021 年Cao 等人提出了一种张量CNN 光谱空间特征完全分离的提取方法［18］，在空间光谱间的双特征提取之上，利用塔克分解和神经网络相结合的两个张量层对多路特征进行分解。分解后的特征张量沿着通道维度连接，分别保存频谱和空间特征。在2022 年kong 等人提出了一种多向CNN 空间光谱间特征提取算法［19］，将特征提取网络划分为三个并行模块。光谱模块用于获得沿光谱方向的光谱特征，其中两个空间模块提取沿两个不同空间方向的空间特征，然后将所有特征融合在一起后进行压缩。以上方法有效地解决空间与光谱间的特征提取问题，但是仍没有解决多光谱图像元素间的长距离关系问题。在2022 年Kong 等人提出一种多尺度空间谱注意力网络［20］，提取出了多尺度的光谱特征，解决了光谱相关性的非平稳性和空间特征的尺度多样性的问题。但是其网络中使用不同尺度的3D 卷积块共同提取光谱与空间特征，两类特征的相关性会相互影响，这样会降低对光谱间特征和空间特征的提取效率，同时也会使模型的参数量过大。

对于多光谱图像压缩以上方法并不能达到高效率同时提取输入图像的空间特征和光谱间特征。一方面，其忽略了特征之间的长距离相关性以及独立性的问题。另一方面，针对空间特征使用普通2D 卷积操作只针对平方块内的元素进行操作，这样的操作会导致一部分空间信息的损失，即局部空间信息的损失。所以现有方法不能同时实现高效的空间和光谱间特征提取。针对此问题，本文提出了一种融合多尺度特征卷积神经网络的多光谱图像压缩方法。通过在编解码器引入多尺度空间光谱间特征提取模块和空间光谱间非对称卷积块，解决特征之间存在长距离相关性以及局部特征信息会被忽略的问题。多尺度空间光谱间特征提取模块使用不同的卷积方式和多尺度的卷积模式来获取元素之间的长距离相关性。该模块在空间特征上采用多个尺度的组卷积模式，以避免与光谱间特征发生混淆。在光谱间特征提取上，使用3D 卷积来提取纵向的光谱信息。同时，在特征提取阶段，采用多个空间残差块和光谱间残差块，以同时高效提取空间特征和光谱间特征。空间光谱间非对称卷积块通过对输入特征进行不同方向的一维卷积来提取局部特征，并进行整合。该网络能够同时高效地提取多光谱图像的空间特征和光谱间特征并对其进行压缩。

2 融合多尺度特征卷积神经网络

2.1 网络结构

多光谱图像输入X进入带有多尺度空间谱间特征提取模块和空谱非对称卷积模块的前向特征提取网络Ga，以提取多光谱图像中的空间特征信息和光谱间特征信息，其过程如下所示：

其中：Y代表经过网络Ga后所得到的特征信息，Wconv，WGDN，WMSSA，WSSC，分别代表卷积操作，广义除法归一化操作以及多尺度空间谱间特征提取操作和空间光谱间非对称卷积操作。多尺度空间谱间特征提取模块被部署在编码器的瓶颈位置，可以在多光谱图像输入的开始阶段有效地提取到多尺度的光谱以及空间信息。空间光谱间非对称卷积模块在提取局部空间特征的同时还可以辅助光谱特征的提取。在获得空间和光谱间特征信息Y后，鉴于熵模型与潜在表示上的先验相对应，潜在表示可以将边信息视为熵模型参数的先验。为了进一步获取边信息Z，将输入Y输入到超优先级分析编码器Ha中进行编码处理，其具体过程可以表示为：

其中：Z是获取到的边信息，Wconv，WRELU，分别代表卷积和LeakyReLU操作，最后Z被量化编码成为比特流，在熵解码端进行处理得到量化后的通过Hs获得所需要的熵参数，其具体过程如下所示：

2.2.1 光谱间特征提取

光谱间特征存在于多光谱图像的纵向上，针对光谱间的特征，采用3D 卷积的方法，3D 卷积操作可以对输入数据进行一维的纵向卷积操作从而提取到丰富的光谱特征。为了更好地提取特征，使用了n个谱间残差块，其基本过程如图4（a）所示，对输入依次进行3D 卷积，激活，3D 卷积操作后与输入相加后进行激活，其具体过程如下：

其中：X为模块的输入代表第n个谱间残差块的输出。Rspe(X)代表谱间残差块的处理过程，WRELU，Wconv3D分别代表激活操作以及3D 卷积操作。在本文中谱间残差块的数量为3。采用两条并行的谱间特征提取路线，以上为其中一条路线的示例，两条并行支路使用不同尺度的卷积核大小提取出不同尺度的谱间特征，卷积核的大小分别为5×1×1 和7×1×1，卷积核的选择在3.4 节介绍，多尺度特征提取完毕后，使用concat操作将两部分输入整合到一起，使用1×1 卷积进行降维操作，用Sigmoid函数对降维后的数据进行归一化处理最后与整合降维后数据做乘积操作得到融合后的光谱特征，过程如下：

其中：X代表输入图像代表经过多个谱间残差块的输出，分别代表经过两个并行的光谱间特征提取支路的输出结果。M，N分别代表两个支路所使用的卷积核的大小，concat操作将两个尺度的特征信息合并起来。Wconv1×1代表卷积核大小为1 的卷积操作，将输入数据的维度转化为所需要的维度。

2.2.2 空间特征提取

针对空间特征的提取方法与光谱特征提取基本一致，为了不与光谱间特征发生混淆，卷积方式采用的是组卷积的方法如图3 所示，输入通道与输出通道均为C/N（图中N取2），在本文中N为192。此操作不仅可以单独提取到空间特征，也减少了参数量。对于空间特征也采取同谱间特征相同的引入残差块的处理，其过程同谱间残差块相同，且引入数量为3，不同的是卷积操作采用的是组卷积，其过程如图4（b）所示。

在空间多尺度方面，引入两条并行路线，卷积核大小分别为5×5 和7×7，其过程如下：

2.2.3 空间光谱间特征融合

在提取到多尺度的空间谱间的特征后对两者进行融合操作，其过程如下所示：

其中：X，，分别代表多光谱图像输入所提取的多尺度的空间信息以及谱间信息。Xout为模块的输出。

在得到空间特征与光谱间特征后，进行与谱间和空间多尺度特征融合相同的操作，用来得到融合后的空间光谱间联合特征，最后与整个模块的输入进行加和操作得到输出的特征信息。

针对普通CNN 图像压缩网络忽略了局部空间信息与光谱信息的问题。提出一种非对称的卷积操作，针对空间方向上的水平和垂直方向以及光谱间的纵向进行一维的卷积操作，提取局部的空间和光谱间特征，将局部关键特征以及光谱间特征集合到方核卷积中，实现全局信息、局部信息和光谱信息的结合。此操作不仅可以得到丰富的局部特征信息，还可以得到光谱之间的特征信息。局部卷积操作如图5所示。

在提取局部空间和光谱间特征的同时，采用一般的2D 卷积提取全局的特征与局部特征相结合获得全面的空间谱间特征。将平方卷积核分解为三个较小的一维卷积核来可以有效地减少模型参数的数量。

模块的结构如图6 所示，基本模块由一个ReLU激活函数和四个卷积层构成，激活函数可以强化输入特征的非线性变换，四个卷积层分别为卷积块为3×3，1×3，3×1 大小的2D 卷积块来提取全局和局部的空间特征，和一个卷积核大小为3×1×1 的3D 卷积块来提取局部的光谱间特征。C1，C2，C3，C4分别代 表3×3，1×3，3×1 大小的2D 卷积操作以及3×1×1 的3D 卷积操作，C1在残差学习的过程中受到C2，C3，C4的影响达到细化提取的局部关键特征，增强图像压缩网络对局部细节的表达能力。使用xi表示第i 个卷积层输出的特征，则SSC 可以表示为：

其中：xi-1为经过SSC 输出的特征张量，O代表SSC 模块的输出。同时SSC 的在编码器和解码器中的输入输出通道均为N。

2.4 熵模型

网络使用了超先验来从潜在表示中捕获副信息，以生成更准确的熵模型。网络采用了高斯尺度混合（GSM）先验概率模型［20］，GSM能够在压缩性能和模型复杂性之间达到更好的平衡，并且时间消耗较少。具体而言，为了确保足够的灵活性以匹配变分后验，通过对预测的GSM和标准均匀噪声进行卷积来计算Y的参数先验概率模型：

在这里ψ(i)表示第i个完全因子化模型，该模型对应于。因此，总比特包含压缩的和，其可以定义为：

3 实验分析

3.1 数据集

为了证明所提出的压缩框架在具有不同波段数量和分辨率的数据集上的有效性，在实验中使用了两个比特深度为16 bit的数据集。

第一个数据集来Landsat-8卫星。由于第8个波段（15 m）的空间分辨率与其他波段（30 m）不同，因此选择前7个波段。原始图像覆盖了中国的不同地区和季节，并被裁剪成128×128大小的10 800张图像进行训练。为了测试，从多个地区选择了16张512×512大小的图像。

第二个数据集是来自Sentinel-2卫星的8波段数据集，其空间分辨率为20 m。同样，选择8 200张尺寸为128×128的图像进行训练，选择16张尺寸为512×512的图像进行测试。在训练集和测试集之间没有相同的图像。所有的测试图像都具有代表性，包含不同比例的各种场景。

3.2 训练条件

本文提到的模型都是由Adam优化器在带有Pytorch的NVIDIA GeForce RTX 3090 GPU上训练。

由于网络中的主要参数和与因子化熵模型相关的辅助参数使用了两个优化器，对于主优化器，学习率被初始化为1×10-4，当在15的迭代内没有看到改善时，学习率以0.1的衰减率降低。

在训练期间，辅助学习率固定为1×10-3。批量大小设置为16。每个模型被训练了大约300次迭代，直到收敛。

训练网络所采用的损失函数为率失真损失函数［11］其中失真损失采用最小均方误差（Mean Square Error，MSE）损失，码率损失采用公式（19）中所使用的码率损失。

3.3 评价指标

实验中既进行了客观评价，也进行了主观评价。使用上文提到的两个数据集，根据广泛使用的峰值信噪比(Peak Signal to Noise Ratio,PSNR)指标，客观地评估了提出的网络架构。具体来说，由于原始图像的比特深度是16 bit，因此PSNR可以通过式（22）得到：

其中：DMSE(X，)为原始图像与重建图像间的最小均方误差。此外，为了测量光谱的恢复质量，引入了一种光谱指标，即光谱角度（Spectral Angle,SA），也称为光谱角度映射（Spectral Angle Mapping,SAM），它测量原始图像和解压缩图像中对应像素的两个光谱矢量之间的角度。对于波段数为c，宽和高为w和h的原始图像X和相应的重建图像SA的表达式如式（23）：

为了方便衡量，由MSA表示的一对图像所有像素的平均SA，即：

在比特率相同的条件下，较大的PSNR值能够表示出更好的压缩性能。相反，较小的MSA值，解压缩的频谱向量越接近原始频谱向量，表明压缩的性能更好。

3.4 多尺度特征提取模块性能测试

多尺度空间光谱间特征提取模块用来提取不同尺度的光谱信息和空间信息进行融合，此操作可以获得特征之间的长距离关系。在此模块中空间和光谱间各选择两个大小的卷积核，分别提取两个尺度的特征信息。

为了选取适合大小的卷积核，对于空间特征提取所使用的卷积核在卷积核大小为5×5，7×7，9×9中进行组合，光谱间特征提取所使用的在卷积核大小为5×1×1，7×1×1，9×1×1中进行组合的条件下进行SSC模块的测试实验，所有实验均在比特率在0.5 bit左右的条件下，并且对Landsat-8数据集进行实验。为了统一标准本文中所使用的比特率是比特/像素/波段。表1和表2分别显示了在不同卷积核大小下模块的性能。

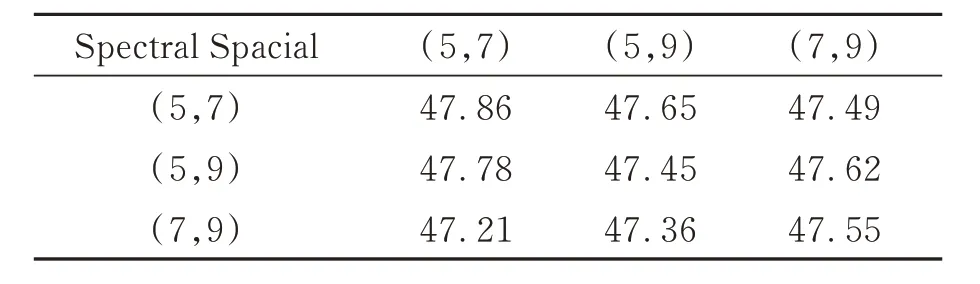
表1 不同卷积核组合下的MSSA模块PSNR指标Tab.1 PSNR metrics for MSSA modules with different convolutional kernel sizes （dB）

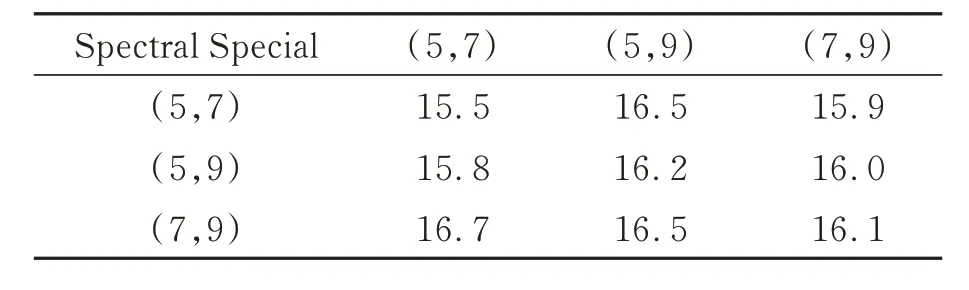
表2 不同卷积核大小下的MSSA模块的MSA指标Tab.2 MSA metrics for MSSA modules with different convolutional kernel sizes （×10-3 rad）

经过实验可以得到在空间光谱间卷积核大小分别在5×5，7×7，5×1×1，7×1×1时此模块会取得最好的效果。将使用此卷积核大小的MSSA模块应用到压缩模型中并且在Landsat-8数据集上测试率失真表现，与深度学习压缩算法Scale-only，Mean&Scale，Joint以及传统算法JPEG2000和3D-SPIHT进行比较，其结果如图7所示。从图像可以看出加入MSSA的压缩网络结果优于其他算法，并且在低比特率下效果更好。

3.5 空间谱间非对称卷积块模块性能测试

对于空间谱间非对称卷积模块，其类似于网络中的基础模块，可以在网络中被多个引入［20］，实验主要目的为测试在Landsat-8数据集下，SSC模块数量为2，3或4，码率为0.5 bit左右时，SSC模块的性能表现，其结果如表3所示。

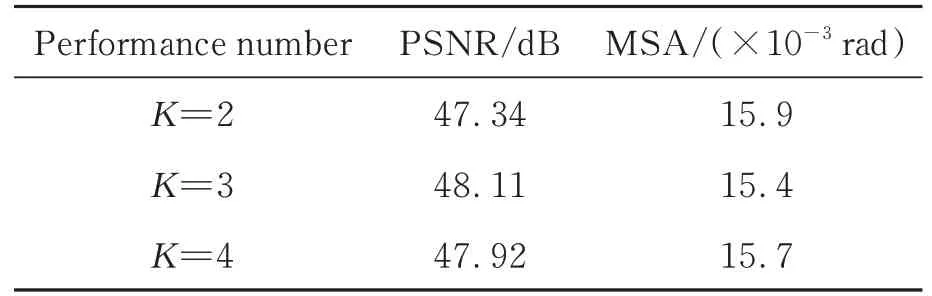
表3 不同数量SSC模块下的SSC模块的PSNR指标和MSA指标Tab.3 PSNR metrics and MSA metrics for SSC modules with different numbers of SSC modules

当引入模块数量为3时网络达到最佳性能。将3个SSC模块应用到压缩模型中并且在Landsat-8数据集上测试率失真表现，其结果如图8所示。从图像可以看出加入SSC的压缩网络结果优于其他算法，并且随着比特率的增大其效果越明显。

3.6 融合多尺度特征卷积神经网络性能测试

上述实验已经验证了MSSA模块以及SSC模块的在多光谱图像压缩方面有效性，在本节中将对其进行综合测试，即对本文提出图像压缩网络结构在Landsat-8的7波段数据集和Sentinel-2的8波段数据集上进行性能测试。图9和图10分别显示了7波段和8波段数据集实验结果。图9比较了Landsat-8卫星数据集上各种模型解压缩的重建图像的PSNR以及MSA。数据显示，提出模型的表现优于其他算法，并随着比特率的增大其效果越明显。

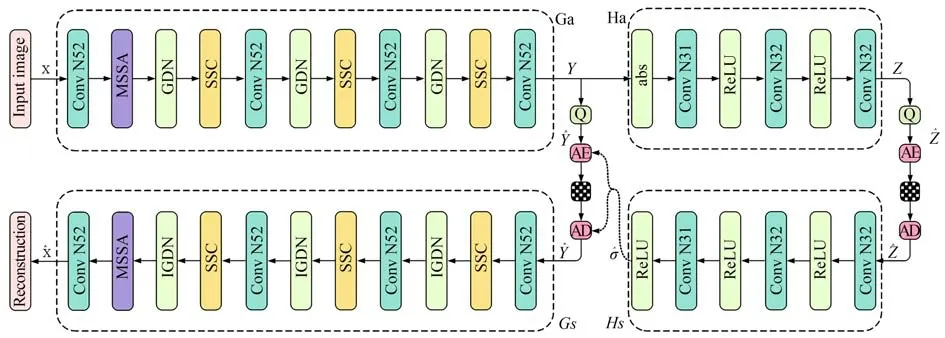
图1 多尺度空间谱间特征提取网络结构Fig.1 Multi-scale spatial inter-spectral feature extraction network structure

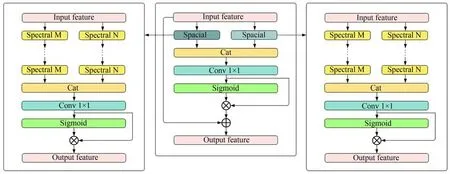
图2 MSSA 模块结构Fig.2 MSSA module structure

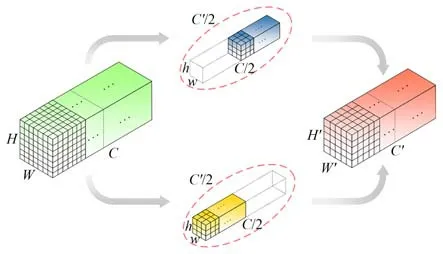
图3 组卷积示意图Fig.3 Group convolution schematic

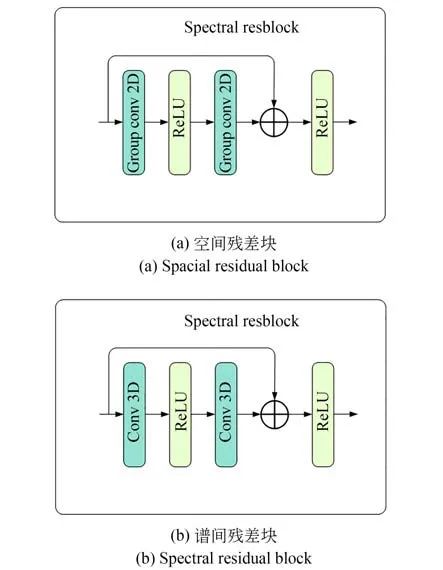
图4 空间和谱间残差块Fig.4 Spacial and spectral residual blocks

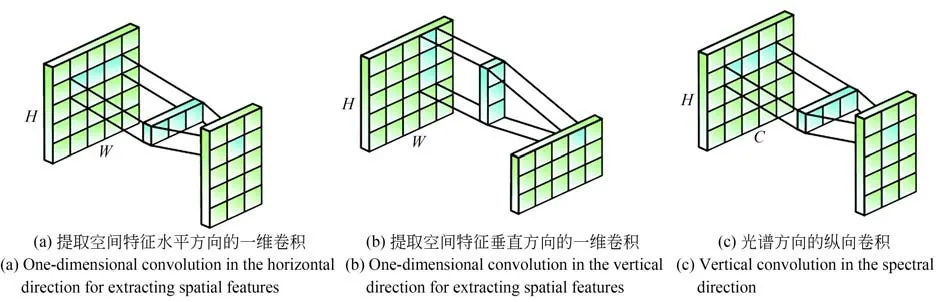
图5 SSC 三种卷积模式示意图Fig.5 Schematic diagram of the three convolution modes of SSC

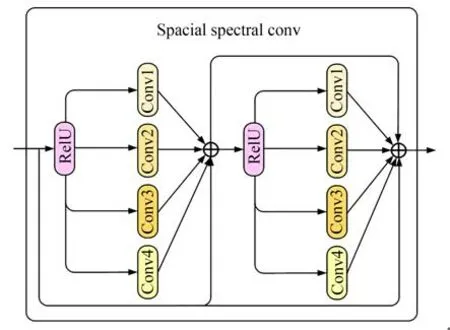
图6 SSC模块结构Fig.6 SSC Module Structure

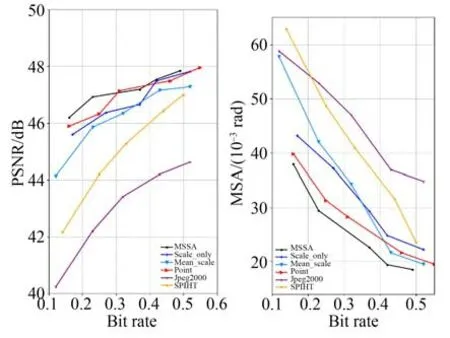
图7 MSSA模块测试结果Fig.7 MSSA module test results

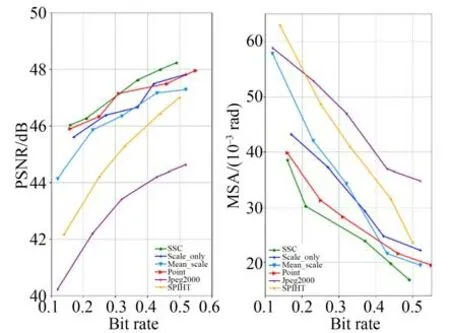
图8 SSC模块测试结果Fig.8 SSC module test results

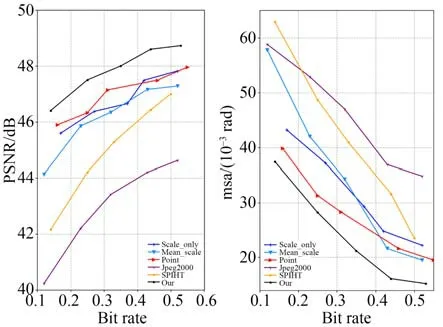
图9 7波段数据的PSNR指标和MSA指标Fig.9 PSNR metrics and MSA metrics for 7-band data

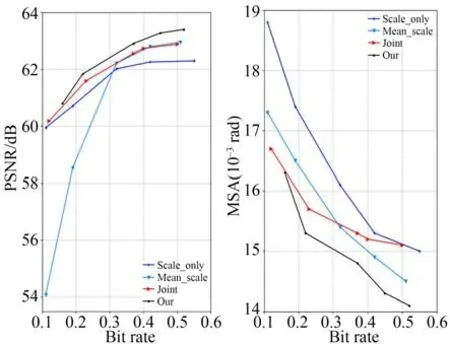
图10 8波段数据的PSNR指标和MSA指标Fig.10 PSNR metrics and MSA metrics for 8-band data

图10比较了Sentialt-2卫星数据集上各种模型解压缩的重建图像的PSNR以及MSA。JPEG2000和3D-SPIHT的数据将在表5中给出。数据显示，提出模型同样表现出最佳性能。提出模型比现有的基于超优先级的模型更优越，尤其是在高比特率下更为明显，这表明更详细的空间和光谱特征可以被所提出的网络有效地捕获。

表4和表5中分别给出了7波段和8波段测试集的PSNR，MSA结果。由于不同方法很难获得相同的比特率，表中给出了6种方法在5种代表性比特率下的结果。此外，通过不同算法以相似的比特率解压缩的重建图像分别如图11和12所示。每个测试图像的一个复杂区域被突出显示，以便进行更清晰的比较，所有图像所基于的比特率在0.4 bit左右。通过提出模型进行解压缩的重建图像包含更多清晰的边缘和纹理，在两个数据集上都提供了最佳的视觉质量。

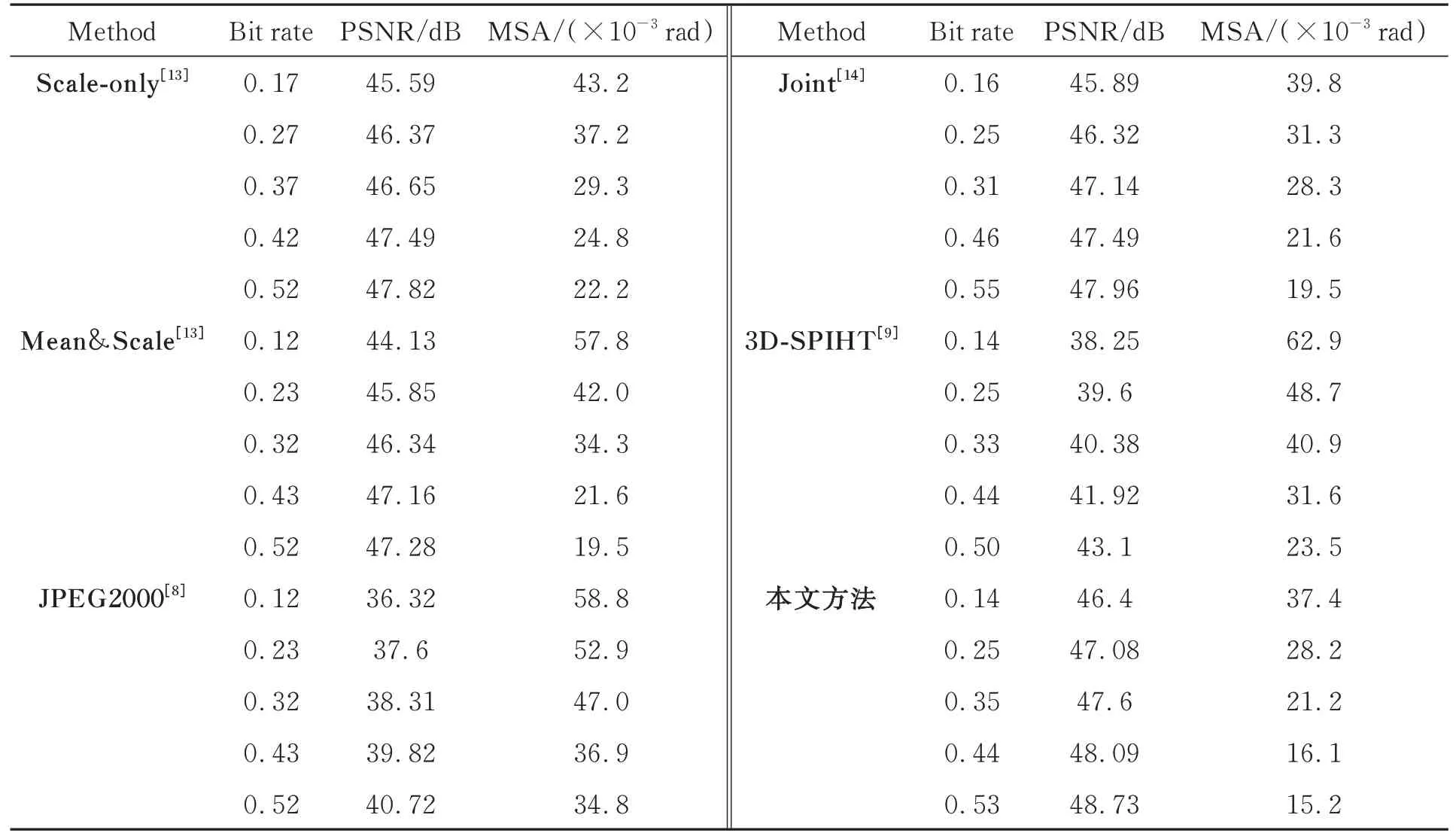
表4 7波段测试集下的PSNR，MSA指标Tab.4 PSNR，MSA metrics under 7-band test set

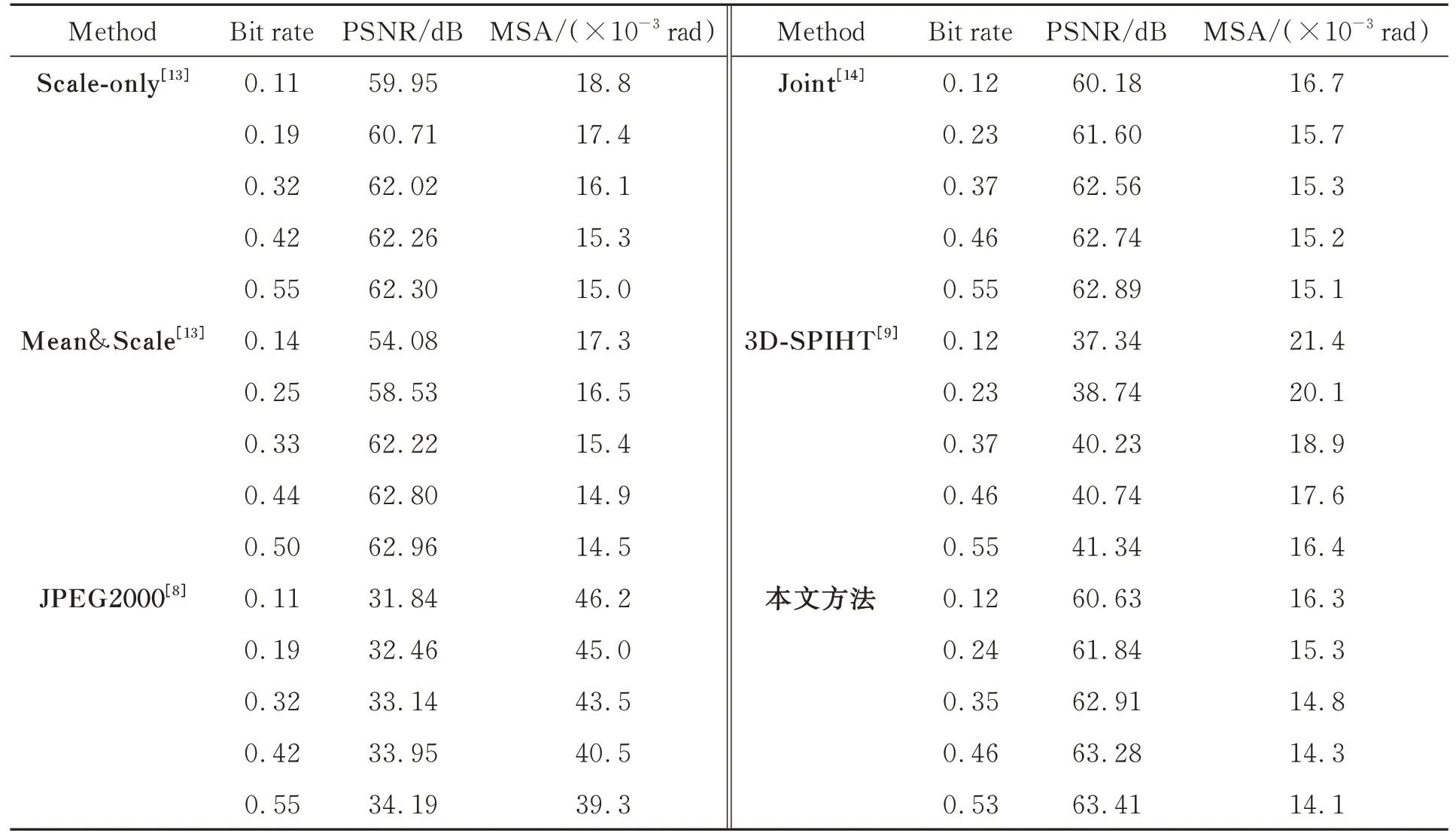
表5 8波段测试集下的PSNR，MSA指标Tab.5 PSNR，MSA metrics under 8-band test set

图11 Landsat-8数据集重建图像示意图Fig.11 Schematic of reconstructed image from Landsat-8 dataset

图12 Sentinel-2数据集重建图像示意图Fig.12 Schematic of reconstructed image from Sentinel-2 dataset

3.7 复杂度分析

对模型复杂性进行比较，表6展示了在Landsat-8数据集下不同算法的编码和解码时间的比较。

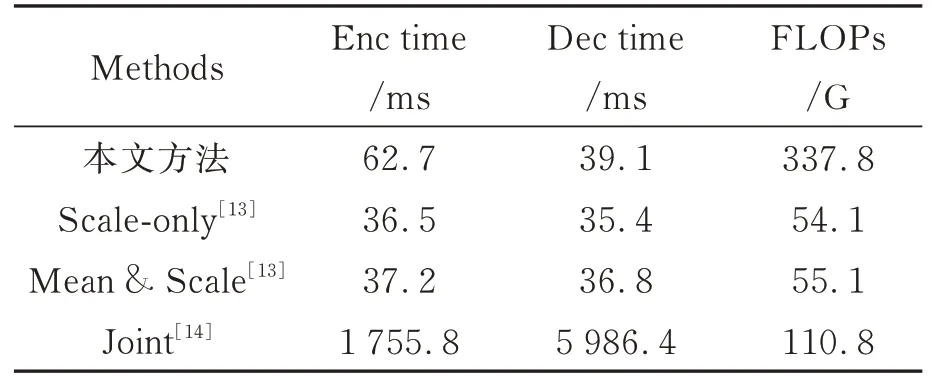
表6 各算法编解码时间及计算量Tab.6 Codec time and computation for each algorithm

表中深度学习多光谱图像压缩算法具有可以在GPU平台下进行并行计算的特点，因此均在GPU平台下测试其编解码时间。

从表中可以看出，由于串行解码的要求和较高的算法复杂性，Joint算法的编码和解码时间较长，计算量较大。相比之下，提出模型、Scale-only和Mean&Scale算法由于并行编解码的特点，具有较低的编解码时间。表格还提供了不同模型的浮点运算次数（Floating-Point Operations per Second,FLOPs）。

需要注意的是，模型的并行度也会影响执行时间，因此一些FLOPs较低的模型可能会消耗更长的编码时间，例如Joint模型。而本文提出模型具有适度的FLOPs，并且在GPU上具有适中的执行时间。该模型在适度的编解码时间和计算量的基础上显著提高了图像压缩能力。

4 结论

在本篇论文中，提出了一种融合多尺度特征卷积神经网络用来压缩多光谱图像。为了提取到多光谱图像中的空间特征和光谱间特征，提出了多尺度空间谱间特征提取模块以及空间光谱非对称卷积网络模块。实验表明所提出网络与传统多光谱图像压缩方法相比，PSNR指标高于传统算法1～2 dB，MSA指标高于传统算法（2～8）×10-3rad，能够更好地提取多光谱图像特征信息，使解压缩图像拥有更清晰的纹理和边缘，提供了优异的压缩性能。并且在模型复杂度以及压缩、解压缩的时间上能够达到更好的均衡效果。