基于多目标规划的供应商订单分配方法研究

王勋　晋严尊

［摘 要］制造企业在进行物资与服务采购时，对多源供应商一般采用固定的订单分配比例，但固定比例分配订单在履约过程中，由于供应商订单与能力未精准匹配，客观造成了一些产品出现质量不稳定、未按时交货的情况。为了使供应商能力和获得订单数量匹配，文章针对多源供应商的订单分配问题建立一种基于多目标混合整数规划模型，该模型可以依据供应商过往的各项能力表现，确定使用的供应商数量和订单分配数量，并考虑实际采购过程中阶梯降价的情况。使用供应商的实证数据进行求解后，结果显示该模型具有良好的准确性和实用性，可以作出科学的采购决策，并为其他制造企业提供借鉴和参考。

［关键词］供应链管理；供应商选择；多目标规划；订单分配；物资采购

doi：10.3969/j.issn.1673 - 0194.2024.02.040

［中图分类号］F274 ［文献标识码］A ［文章编号］1673-0194（2024）02-0123-04

0     引 言

随着我国社会经济不断发展，对外开放程度不断加深，大型制造企业在参与市场竞争、提高生产效率的过程中，需要担任现代产业链链长的角色，引领核心领域的创新发展，实现向高质量现代化经济的迈进。而这些离不开供应链上各家企业的密切合作，特别是以物流、资金流、信息流为纽带的互联互通，支撑了整个产业链的发展。因此，为了科学规范管理物流、资金流、信息流3个关键要素，使用科学的方法对供应商订单进行合理分配十分必要。

在供应商的订单分配领域，纳拉辛汉（Narasimhan）和斯托伊诺夫（Stoynoff）［1］在1986年就以总量固定、在供应商之间分配数量不固定为背景，进行了典型的确定性订单量分配问题研究。戈德锡普尔（Ghodsypour）和布莱恩（Brien）［2］在多个准则约束和供应商能力有限的情况下，建立了一种多目标非线性混合整数规划模型来处理采购量分配问题。库玛（Kumar）等人［3］提出了模糊多目标供应商选择及其采购量分配问题的模型。国内学者对采购领域的研究起步相对较晚，但也取得了亮眼的成果。朱建军、刘士新、王梦光等［4］提出了基于层次分析法、数据包络分析法以及多目标规划的混合模型，并将其应用于供应商选择和采购量分配的决策分析之中。吴锐、周焯华等［5］通过基于绩效改进的方法解决了多供应商选择和采购量分配问题。晋严尊、汤辉等［6］研究了智能制造技术在机载武器制造中的应用，推动企业的转型升级和创新发展，采购作为智能制造环节的前端，也需要使用科学的管理方法。段喆、朱道立［7］研究了多阶段的供应商选择与采购量分配的混合整数规划模型及其求解方法。国外学者［8］研究了在实施多供应商采购的情况下，采购品种和数量在供应商中的分配策略。在此之后，复杂的求解算法开始被纳入学者的研究领域。王贤斌、周宝刚［9］提出了一个关于供应商选择和采购量分配的、集成的模糊规划模型。范志强［10］建立了确定的多目标、多周期订单分配模型，其目标函数包括总交易费用、总采购成本、次品数量、延迟交付数量和供应商信誉评分。

本文构建了一种多目标混合整数规划模型，利用与供应商合作过程中产生的数据来衡量未来的合作潜力，并以供应商的能力上限、所给出的优惠价格综合考虑，将订单在供应商之间进行合理分配，以保障企业的产品供应能力，从而在愈发激烈的市场竞争中取得优势。

1     建立多目标混合整数规划模型

1.1   建立多目标混合整数规划模型的主要原则

在考虑企业进行采购时，以供应商以往的绩效为依据，确定供应商能力与订单分配数量之间的匹配关系。为了确保匹配方法是最优的，需要一个模型来决定要使用的供应商数量，以及它们之间的订单数量分配。该模型需满足以下条件。

目标函数：总采购花费最小、质量合格数量最多、准时交货数量最多、满足服务水平数量最多。

约束条件：总的采购数量=总需求数量，单个供应商的供货数量不超过其最大供货能力，每个供应商的供应量与其对应的价格区间相匹配，不允许负的采购量。

将需求总量表示为D，该数值在进行采购之前即通过实际需求而确定下来。假设有i个供应商来参与竞标，则分配给第i个供应商的订单比例为xi，则第i个供应商的质量、交付周期、服务水平分别以qi，ti，si表示，第i个供应商报出的价格为pi。

1.2   考虑阶梯价格折扣的因素

在企业的采购中，规模效应是不可被忽视的，价格折扣作为常见的一种协调买卖双方利益的机制，被众多企业所采用。在本文中，采用全额数量折扣为例来计算。

价格折扣可用公式表示为

（1）

式（1）中，j表示折扣阶段；aij表示供应商i在j折扣阶段采购产品的上限；xij为供应商i在j阶段采购产品的数量。

1.3   模型建立

针对一种产品在多个供应商处采购，根据采购量给予分阶段优惠的情况，建立如下模型：

（2）

（3）

（4）

（5）

（6）

（7）

（8）

（9）

（10）

xij≥0（11）

在上述表达式（2）到（11）中，pi为产品的正常价格；qi为供应商提供产品的合格率；ti为供应商所能提供的准时交货率，si为供应商的服务水平满意率。D表示需要采购产品的总量；yij表示值为0～1的整数决策变量，该值为1表示从供应商i在j优惠阶段采购产品，0表示未在供应商i处采购产品。表达式（2）代表企业在多家供应商处购买产品的总费用最小；表达式（3）代表所购买的产品中合格的数量最多；表达式（4）代表所购买产品中准时交货的数量最多；表达式（5）代表达到服务水平的产品数量最多；在表达式（6）中，代表采购的产品总数量等于需求方提出的产品总量；表达式（7）代表每家的供应商采购量应当在该供应商的供应能力之内；表达式（8）代表某供应商获取的产品采购量应该与对应的折扣阶段的数量范围一致；表达式（9）代表采购产品的价格只能在折扣的某个阶段而不能占据多个各个价格阶段进行采购；表达式（10）代表整數的0-1变量；表达式（11）代表为符合实际情况，采购量不可为负数。

2     多目標混合整数规划模型实例求解分析

在某型航空产品的配件采购过程中，假定采购需求量为12 500件。已提前精选出3家供应商，这3家供应商的质量合格率、准时交付率、服务满意率、供应能力、价格折扣率及优惠区间数据见表1。

由于求解的目标函数为多目标函数，且含有0～1整数参数，在实际的采购过程当中，物品的购买数量也都是整数，根据实际情况，增加了约束条件表达式（12）、（13），其中表达式（12）代表为降低单一来源的供应风险，每家供应商至少获得15%的订单数量；表达式（13）代表为了便于厂家生产时进行组批，每个厂家获得的订单数量为50的倍数。

（12）

50|xij（13）

求解多目标混合整数规划模型，常见的方法有主要目标法、线性加权法、逼近目标法。通过对公司采购专家的调查走访以及参照公司相关的管理要求，对多目标函数进行线性加权法求解，目标函数中总采购成本、质量、准时交货、服务水平等4个指标的权重分别为0.1、0.4、0.4、0.1。基于此，可使用线性加权法进行求解，因此将目标函数简化为

（14）

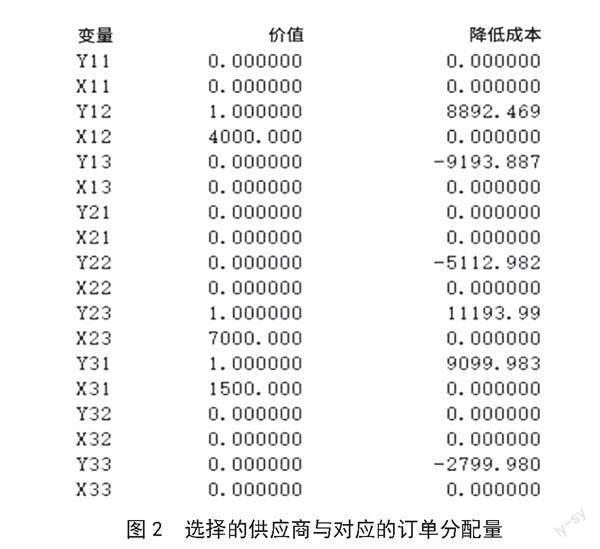
目标函数简化之后，可以将多目标函数转化为单目标函数求解。在优化后的模型转换为编码输入Lingo中，并带入表格中的数据，运行之后可以得到模型的运行结果（见图1），选择的供应商与对应的订单份额分配（见图2）。

由以上结果我们可以得知，本次选择的A、B、C，3个供应商订单分配结果为：在A供应商的第二个折扣阶段订购4 000个，在B供应商的第三个折扣阶段订购7 000个，在第三个供应商的第一个折扣阶段订购1 500个。总采购金额为189 888元，并在指标比例固定的情况下满足了多目标函数求解的要求。

3     研究结论

本文考虑到一般制造型企业的采购是一个包含阶梯价格的多目标混合整数规划问题，并且多个目标函数之间重要性不同甚至互有冲突，为了能够兼顾各个目标以及企业运行的实际情况，使用了线性加权法来处理该问题，将多目标混合整数规划问题进行转化，以便于用Lingo软件进行运算求解。由本文结果可以看出，该方法不仅适用于有阶梯降价采购的类型，对于无折扣优惠的采购过程，也具有很强的适用性，可为其他制造企业的采购过程提供参考和借鉴。

主要参考文献

［1］NARASIMHAN R，STOYNOFF K.Optimizing aggregate procurement allocation decisions［J］.Journal of Supply Chain Management，1986（1）：23-30.

［2］GHODSYPOUR S，OBRIEN C.A decision support system for supplier selection using an integrated analytic hierarchy process and linear programming［J］.International Journal of Production Economics，1998（20）：199-212.

［3］KUMAR M，VRAT P，SHANKAR R.A fuzzy goal programming approach for vendor selection problem in a supply chain［J］.Computers & Industrial Engineering，2004（1）：69-85.

［4］朱建军，刘士新，王梦光，等.供应商选择及定购计划的分析［J］.东北大学学报，2003（10）：956-958.

［5］吴锐，周焯华，何小洲.基于绩效改进的供应商群及其采购量的选择［J］.重庆大学学报（自然科学版），2003（10）：

148-151.

［6］晋严尊，王中一，汤辉，等.智能制造技术在机载武器制造中的应用［J］.航空兵器，2021（6）：1-6.

［7］段喆，朱道立.多阶段多产品供应量分配的综合模型［J］.系统工程，2004（6）：21-24.

［8］KAWTUMMACHAI R，HOP N.Order allocation in a multiple-supplier environment［J］.International Journal of Production Economics，2005：231-238.

［9］王贤斌，周宝刚.采购量分配决策模糊规划模型［J］.运筹与管理，2007（4）：157-159.

［10］范志强.供应链订单分配优化模型及其模拟退火算法［J］.计算机工程与应用，2012（25）：28-33.

［收稿日期］2023-06-08