基于固定时间稳定与部分状态反馈的角度约束制导律
许 琛,牛智奇,骆 盛,杜凤怀,韩 迪,王 洋
(1 西安现代控制技术研究所,陕西 西安 710065;2 西京学院计算机学院,陕西 西安 710123)
0 引言
比例制导律作为一种经典的制导方法已经被广泛应用于各类导弹的制导系统设计中[1]。但是,传统比例制导律存在着突防能力较弱、鲁棒性不强等问题,这些都对制导算法的性能提出了更高的要求。如果采用终端约束角度的方式来打击目标,既可以提升突防效果,也能优化毁伤效能,实现这种攻击方式的制导方法就是角度约束制导律[2]。
为了提升角度约束制导律的性能,许多学者基于先进控制理论开展了相关研究。其中,王洋等[3-4]为了提升角度约束制导律在目标机动、未建模动态等不确定干扰下的鲁棒性能,提出了基于滑模控制、自适应控制等方法的角度约束制导律。而近年来,随着有限时间控制理论的发展,Ding等[5]提出了基于有限时间稳定方法的角度约束制导律。相比于传统渐进稳定方法,有限时间角度约束制导律可以实现制导误差的有限时间,保证了收敛的快速性与高精度。Zhang等[6]将有限时间控制与滑模控制结合,设计了有限时间角度约束制导律。为解决传统有限时间滑模控制的抖振问题,基于有限时间收敛二阶滑模控制方法,郭建国等[7]设计了连续无抖振的有限时间收敛的角度约束制导律。目前,有限时间角度约束制导律仍然存在两方面的问题:1)其收敛时间与系统初值有关,当初值较大时收敛速度可能会受到影响;2)现有方法都是采用全部状态进行反馈,而实际上,部分导弹状态可能是难以测量,同时由于体积以及成本等的限制,存在导弹的导引头无法直接测量视线角速率以及相对距离变化率的情况[8]。
近年来,固定时间控制理论得到了发展[9-10]。基于固定时间控制理论,Cheng等[11]针对固定目标设计了角度约束制导律。Tian等[12-13]针对机动目标设计了固定时间角度约束制导律。另一方面,观测器技术的发展为开展部分状态可测的制导律设计提供了基础[14]。基于高增益状态观测器实现了部分状态可测下的制导系统渐进稳定[8]。王洋等[15]基于线性扩张状态干扰观测器实现了部分状态反馈的高速拦截弹制导控制一体化设计。
文中在视线角速率以及相对距离变化率不可测条件下,提出一种固定时间收敛角度约束制导律。首先,基于一致精确鲁棒微分器(URED)算法设计了一种固定时间状态观测器来估计不可测的系统状态。随后,设计了固定时间收敛的积分滑模面,并提出了固定时间制导律,继而基于固定时间稳定理论证明了闭环系统的固定时间收敛特性。最后,仿真验证了所提出方法的有效性。
1 制导模型
如图1所示,点T表示目标,点M表示导弹。导弹的位置为(xM,yM),目标位置为(xT,yT)。vM表示导弹的飞行速度,vT为目标的速度,ϑM与ϑT分别为导弹与目标的弹道倾角,r为弹目相对距离,q为视线角,aM与qT分别为导弹和目标的法向控制加速度。
导弹和目标的相对运动方程为:
(1)
导弹和目标的位置变化为:
(2)
由此建立导弹-目标相对运动方程。
由式(1)可得推出:
(3)
(4)
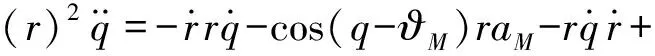
(5)
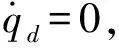
(6)
2 模型转换及相关引理
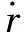
(7)
其中
(8)

定义1:针对如下的系统
(9)
式中x(t)为系统变量。对于任意初始状态x(0)∈R,如果当时间t≥tf时系统状态x(t)=0,同时都存在正常数Tm使得tf≤Tm,则称上述系统为固定时间收敛的。
引理1(URED算法)[9]:考虑如下的系统:
(10)
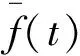
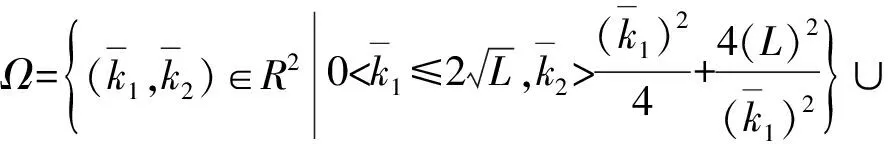
(11)
随后可以得到如下两个结论:
1)结论1:定义如下的Lyapunov函数:
V1=σTPσσ
(12)

(13)
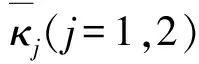
2)结论2:系统状态σ0及σ1将在有限时间tf内收敛到0。同时,收敛时间tf上界满足tf≤Tf,max,其中tf,max为正常数且与初始状态σ0(0)及σ1(0)无关。
证明:引理1的证明见文献[9]的附录A及B。
引理2[10]:考虑如下的系统:
(14)
其中e为系统状态。如果常数参数满足Kp>0,Kd>0,Lp>0,Ld>0,0<α1<1,α2=2α1/(α1+1),β1=2α1+1且β2=(2α1+1)/(α1+1),同时系统的初始状态e(0)是有界的,则系统状态在固定时间内收敛:
(15)
te≤Te
(16)
这里Te是一个与系统初始状态无关的正常数。
证明:引理2的证明见文献[10]的定理3.1。
3 制导律设计
3.1 固定时间状态观测器设计
根据引理1,设计如下的固定时间状态观测器:
(17)

下面进行观测器的稳定性分析。
(18)


(19)
综合式(18)与式(19),可得:
(20)
考虑到(20)满足引理1的式(10),同时选取参数ρ2>0且ρ1与ρ3满足如下参数域:
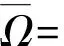
(21)
3.2 制导律设计
基于固定时间状态观测器式(17)的估计值,并受引理2启发,可以设计如下的固定时间收敛滑模面
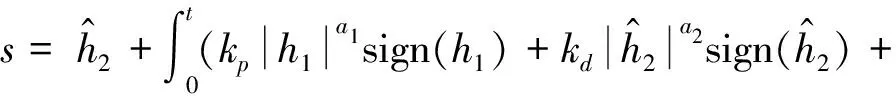
(22)
式中:a1,a2,b1及b2为正常数,并将在后面的定理1定义它们的取值。对s求取导数并考虑式(17)可得:
(23)
其中
(24)
随后,可以设计如下的部分状态反馈固定时间制导律:
(25)
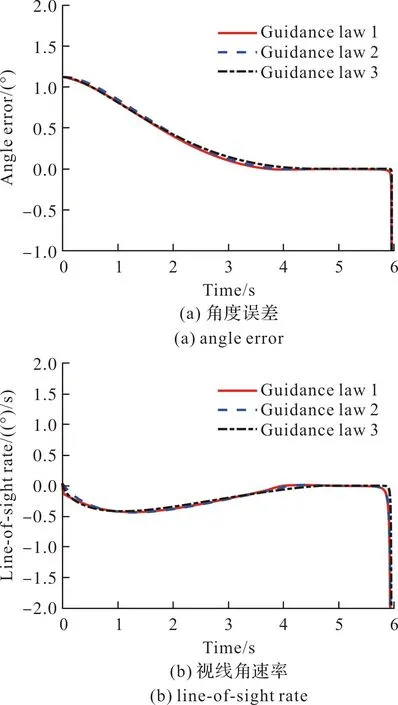
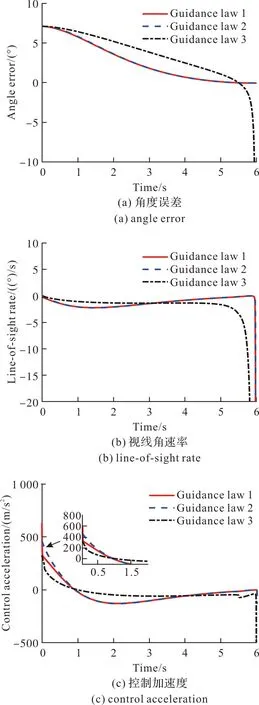
式中TP,a及dSP为正常数,且0 定理1:对于式(7)系统,采用式(25)制导律,如果选取参数kp>0,kd>0,lp>0,ld>0,0 h1=0,h2=0,ift≥thf (26) thf≤Thf (27) 式中Thf是一个与系统初始状态无关的正常数。 证明:将制导律式(25)代入式(23),可得: (28) 选取如下Lyapunov函数Vs: Vs=s2/2 (29) 对Vs求导,同时考虑式(28)可得: (30) 则可得: (31) 假设Vs(ts)=0,从t=0到t=ts对式(31)进行积分可得: (32) 考虑到0≤arctan(2Vs(0))≤π/2,因此从式(32)可知: ts≤TP (33) 因此 s=0,ift≥ts (34) ts≤TP (35) 则 (36) 同时考虑式(22)及定理1,式(36)可得: (37) (38) 根据引理2,只要选取参数kp>0,kd>0,lp>0,ld>0,0 (39) (40) (41) (42) 基于文献[4,6],可设计如下的有限时间滑膜面: (43) 同时设计如下的有限时间制导律: (44) 其中选取参数k1=0.1,k2=0.24,φ1=0.22,φ2=0.37,k3=0.05,k4=0.05,φ3=0.3,k5=0.001。 所提出的观测器式(17)的参数选取为ρ1=5,ρ2=1,ρ3=2,滑模面式(22)参数选取为kp=0.1,kd=0.275,lp=1.6,ld=0.85,a1=0.45,所提出的部分状态反馈固定时间制导律式(25)参数选取为TP=2,a=0.1,dSP=0.001。 同时,为了对比部分状态反馈与全状态反馈的效果,在h2可测的情况下,将所提出的制导律改造为如下的全状态反馈固定时间制导律: (45) 其中 (46) (47) 全状态反馈固定时间制导律的参数kp,kd,lp,ld,TP,a,a1,dSP与前面的部分状态反馈固定时间制导律参数相同。 (48) 式中参数ξ取80。 为了方便表达,分别标记3种制导律: 1)Guidance law 1,固定时间制导律(部分状态反馈); 2)Guidance law 2,固定时间制导律(全状态反馈); 3)Guidance law 3,有限时间制导律。 考虑如下两个场景: 1)场景1(小初始误差),考虑期望角度为qd=-83°,即初始角度误差h1=1.124°。 2)场景2(大初始误差),考虑期望角度为qd=-83°,即初始角度误差h1=7.124°,因此,场景2的初始角度误差是场景1的近6倍。 场景1与2的仿真结果分别见图2及图3,同时收敛时间汇总在表1,脱靶量汇总在表2中。 表1 收敛时间Table 1 Convergence time s 表2 脱靶量Table 2 Off target m 图2 景1仿真结果Fig.2 Simulation results for case 1 图3 景2仿真结果Fig.3 Simulation results for case 2 从图2(a)、图2(b)及表1的数据可知,3种方法都能保证角度误差h1及视线角速率误差h2在5 s内收敛到0。从图2(d)可知所提出的固定时间状态观测器可以保证估计误差在0.1 s内收敛到0。同时,从表1可知,3种方法都能保证导弹脱靶量不高于0.25 m,可以满足打击精度要求。因此在场景1下3种制导方法都能取得近似的控制效果。 从图3(a)、图3(b)及表1可以看出,当初始角度误差扩大到7.124°之后,所提出的固定时间制导律仍然可以保证角度误差h1及视线角速率误差h2在5 s内收敛到0,而有限时间制导律无法在制导时间段内保证角度误差h1及视线角速率收敛到0。产生这样结果的原因是有限时间制导律收敛时间与初始误差相关,当初始误差加大时其收敛时间也将随之加大。而固定时间制导律始终能够保证收敛时间的上限与初始误差无关。从表2还能看出,由于制导误差无法收敛到0,有限时间制导律的脱靶量远远大于固定时间制导律。从图3(d)可知所提出的固定时间状态观测器仍然可以保证估计误差在0.1 s内收敛到0。此外,从图2、图3及表2的结果可以看出,对于采用部分状态反馈的固定时间制导律与采用全状态反馈的固定时间制导律两种方法来说,它们的制导误差收敛效果及脱靶量都基本相同,因此所提出的方法可以在仅使用部分状态反馈的情况下实现固定时间制导效果。 文中提出了一种采用部分状态反馈的固定时间收敛角度约束制导律。其制导误差收敛时间的上界不受初始制导误差影响,可以在各类初始条件下都能保证快速收敛性能,且只需部分状态进行反馈,可以有效简化制导系统的硬件组成。 由仿真对比看,在大初值条件下,所提出的制导律相比于有限时间制导律能取得更快的收敛速度与更小的脱靶量;同时,在部分状态反馈的条件下,所提出的制导律只采用部分状态反馈就可以取得与全状态反馈方法基本相同的收敛速度与脱靶量。 文中只针对二维纵向平面场景开展了研究,未来需要将该方法扩展到三维场景中。此外,利用sigmoid函数代替符号函数会牺牲一定的性能,拟开展理论分析,进一步提升制导精度。
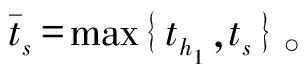
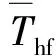

4 仿真验证


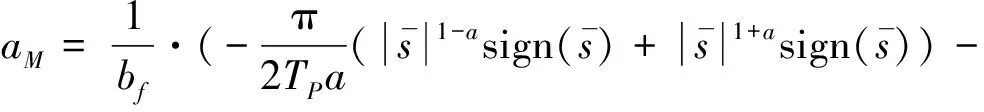

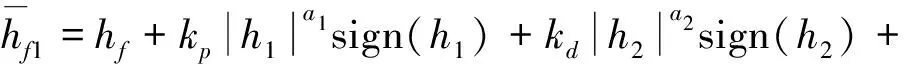

5 结论

