径向压缩下舱体连接电缆力学行为研究

郝予琛，许 斌，张晓宏，刘 广，孙文钊，李昱霖，许 泉，林木森

(1 上海机电工程研究所，上海 201109；2 清华大学核能与新能源技术研究院，北京 100084)

0 引言

飞行器是集成大量结构、机构、电气、电子的具有高价值的复杂机电产品[1],其中电缆的可靠性与安全性关系到飞行器各个分系统能否正常工作[2]。如果电缆在制造、安装与运行等环节中由于机械变形而导致电缆发生损伤,就可能影响飞行器电气功能甚至导致飞行任务失利,因此开展电缆机械特性研究对于提升电缆乃至整个飞行器可靠运行性能具有重要的理论与工程价值。

目前,国内外学者对于电缆的力学特性的研究主要集中在拉伸、弯曲、扭转等基础变形领域。邓腾飞等[3]面向新能源汽车高压电缆开展了拉伸与弯曲分析,发现导线上的应力不均匀使得缆芯结构出现相互分离的趋势。李林书等[4]同样关注了车用充电电缆在弯曲过程中表现的轴向滑移,发现由于电缆本身较短,这种滑移可能会导致导线与接头的连接失效。刘子惠等[5]总结了新型海底电缆在拉伸、弯曲、扭转工况下的损伤变形,重点关注了内部光单元的应变。胡玉娇[6]考虑了船锚对海底电缆钩挂和锚砸的影响,并提取内部铜导体应力,发现远离挤压处的结构更容易遭到损害。除此之外,周又和教授课题组[7-9]对超导电缆的相关力学特性研究也具有较高的参考价值。

对于飞行器连接电缆来说,极易在设备挤压作用下承受径向压缩载荷。更为重要的是,飞行器连接电缆一般不能够像海底电缆那样通过光纤传感技术进行实时稳定的应力应变检测,设计人员很难判断甚至发现损伤情况,这意味着更需要对其机械损伤行为展开详细研究。

针对上述问题,文中以飞行器舱体连接电缆为研究对象,首先基于接触理论建立电缆接触模型以描述内部导线间的接触和摩擦行为,采用数值试验方法模拟径向压缩载荷下的机械特性,并开展试验验证工作,为电缆损伤监测与判断提供理论参考。

1 接触理论

电缆作为包容结构在挤压变形过程中存在复杂的接触关系,建立内外部接触是问题的关键。图1展示了电缆内外部的接触关系,主要包含两类:一类是边界1与边界2的相互作用以及边界2与导线的相互作用;另一类是由于电缆内部诸多导线之间的相互作用。

图1 电缆接触模型示意图Fig.1 Contact model of cable

目前处理这类接触关系的方法包含DEM(discrete element method)[7]以及罚函数法。DEM法主要是将导线截面等效为二维圆形颗粒,建立相应的软球模型[10],将颗粒间的法向力模型等效为弹簧和阻尼,切向力模型等效为弹簧、阻尼和滑动器,用于传递力与位移。颗粒与边界的接触则基于林木森等[11-12]提出的FEM-DEM(finite element method-discrete element method)耦合法。DEM在处理大量颗粒时具有建模与计算效率的显著优势,但是所需关键参数较多,如法向和切向方向上的弹性系数与阻尼系数等[13],对整体计算带来了不确定性。

采用罚函数算法建立相互作用关系,边界1与边界2的相互作用、边界2与内部导线摩擦系数设置为0.5。在罚函数接触格式中,采用标准的格式可能会导致单元侵彻产生显著负滑移能,因此采用基于段接触(Segment-based Contact)的罚函数格式[14-16],用于检测段与段之间的接触或侵彻,其接触刚度kcs可表示为:

(1)

式中:Δtc是当前时间步;FSIP是滑移界面罚函数缩放因子;FM,FS分别是主面和从面罚函数缩放因子。如图2所示,由于无法通过检测节点判断接触,而基于段接触算法能够良好捕捉到接触。为避免计算过程中导线材料承受大变形出现负体积导致计算终止,设置Contact_interior算法以考虑实体单元内表面层之间的接触,罚函数刚度k可表示为:

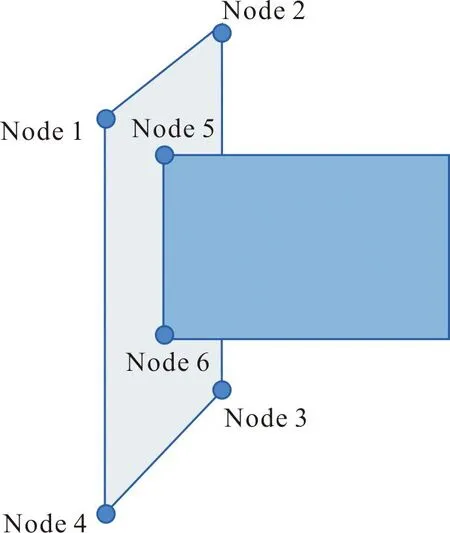
图2 段接触示意图Fig.2 Illustration of segment-to-segment contact

(2)

式中:FP是罚函数缩放因子;V是实体单元体积;E是本构模量;Tmin是实体单元最薄方向的尺寸。

2 结构及有限元模型

以航空航天典型军绿色电缆作为研究对象,电缆从外到内依次为锦纶丝套、生料带、内部导线。锦纶丝套采用编织结构,具有良好的柔软性,用于保护内部导线,标称内径为12 mm,壁厚为0.45 mm。生料带辅助锦纶丝套捆束内部导线,二者共同对内部导线起到约束作用。考虑到生料带的厚度仅为0.05 mm,远小于锦纶丝套的厚度,因此在建模过程中将生料带厚度及弹性模型等效在锦纶丝套上。电缆内部共有19根导线,型号为辐照交联乙烯-四氟乙烯共聚物绝缘电线,直径约2 mm。假设导线在电缆内部按照蜂窝状排布,因此建立典型的电缆三维模型如图3所示。

图3 电缆三维模型Fig.3 Geometry model of cable

绝缘结构直接决定了导线的安全,因此是本研究关注的重点,参考文献[2]中所选用的交联聚乙烯材料建立有限元模型,密度为0.95 g/cm3,弹性模量为600 MPa。网格类型选择Solid实体单元,在划分网格时以六面体为主,网格密度设置为0.5 mm。锦纶丝套属于布料、织物类材料,只承受面内张力而几乎不具有抗弯刚度,因此网格类型设置为Belytschko-Tsay膜单元。电缆有限元模型共包含节点数60 553,单元数47 040。

3 电缆挤压过程边界条件

下面研究电缆在左侧凸台限位下受到来自右侧的设备挤压的工况,利用上述所建立的电缆有限元模型,使用显式有限元算法模拟横向载荷下变形。由于凸台和设备的刚度远大于电缆,在挤压过程中,前二者几乎不会发生变形,可以假设为刚体。计算开始时,电缆和左侧凸台相互接触但没有相互作用力。在边界条件中,左侧凸台固定,右侧设备沿着舱体轴向方向移动,与电缆发生接触并继续挤压电缆,直至设备安装到规定位置,因此设备施加位移加载条件,移动距离为10 mm。电缆的挤压长度相对于电缆全长是比较小的,为提高计算效率,电缆模型长度取挤压区域长度3倍,并在电缆的两端设置对称约束,约束轴向方向的位移和径向方向的转动。整个边界条件如图4所示。

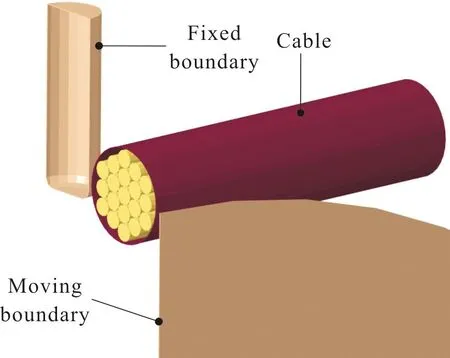
图4 电缆计算模型剖视图Fig.4 Finite element model (section view)

4 结果与讨论

4.1 计算结果

在电缆受到径向压缩载荷的过程中,电缆整体上表现出明显的流动性。图5为当右侧设备沿电缆径向压缩位移分别取2.5 mm,5 mm,7.5 mm,10 mm时,锦纶丝套及内部导线的形状及位置分布,可以看到大多数的导线发生复杂的接触和摩擦,由于锦纶丝套的约束作用很弱,原本圆形截面的电缆最终变形为蝴蝶形。

图5 不同压缩深度下电缆受压变形Fig.5 Deformation of cable during the compression processing

当位移加载到10 mm后,观察到有一根电缆刚好被夹在在左侧凸台和右侧设备之间。从图6可以发现,被夹住的导线在接触位置具有最大应力值为158.26 MPa,应力大小远大于其他导线,也就是整根电缆中变形最严重的位置,其他位置的导线应力则相对较小。

图6 导线应力云图Fig.6 Stress contour of wires

4.2 电缆初始位置影响作用分析

当右侧设备挤压电缆时,电缆的初始位置是影响挤压变形结果的重要因素,因此为了尽可能表征电缆的挤压特性,以电缆与左侧凸台的相对高度作为设计变量,以4.1节的位置作为基准,以2 mm为间距,分别探索电缆相对高度偏移为-4 mm,-2 mm,0 mm(基准),2 mm,4 mm时受到径向载荷时的机械特性差异。

当电缆处于不同相对高度时,电缆变形的剖视图如图7所示,可以看出,当相对高度为-2 mm时,电缆挤压状态和4.1节中的基准高度的挤压状态比较接近,都是呈现出具有中心对称性质的蝴蝶形状;当相对高度为2 mm和-4 mm的时候,电缆只有小部分被挤压,形状呈现出一端小一端大的蝴蝶型。

图7 不同初始位置下电缆变形剖视图Fig.7 Comparison of cable deformation under different initial conditions

从图8所示的电缆与导线的应力数据图上可以看出,导线在相对高度为2 mm的工况中具有最大的应力,结合图6来看,被挤压的导线位于蝴蝶形的一侧,且数量仅有一根,这成为内部导线受压最危险的工况。同样,相对高度为-4 mm的工况中,由于变形模式与2 mm非常接近,导线应力也高于基准高度的应力。对于相对高度为4 mm的工况,电缆在刚刚被设备接触时就被弹开了,因此在后续装配过程中没有被设备挤压,在应力云图中也可以看到内部导线和锦纶丝套都没有产生应力。

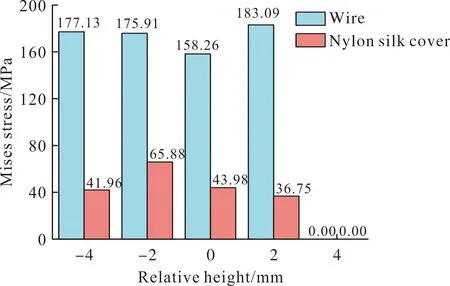
图8 不同相对高度时的应力值Fig.8 Stress value under different initial conditions

4.3 验证试验

为了验证电缆挤压特性,将电缆预先放置在飞行器舱体的凸台附近并装配设备,通过图像采样装置记录相关变形数据,并设置额外的光源以提升拍摄质量。通过数次装配试验,观察到电缆的挤压模式主要有以下两类:1)电缆的大部分区域被挤压在凸台和设备之间,由于挤压区域较大,在装配时,对设备提供了明显的反作用力,在此情况下人工不会继续进行装配。2)电缆的小部分区域被挤压在凸台和设备之间,如图9所示,由于被挤压区域很小,对设备的反作用力也较小,人工装配过程中往往难以察觉,成为了仪器舱装配时最可能发生的情况,也是电缆最危险的工况。从图中可以看到,电缆所表现初的变形模式类似于4.2节中所计算的相对高度为2 mm和-4 mm的工况,内部导线可能承受最大载荷,通过试验与数值计算的结果进行定性对比,验证了数值模型的可靠性。在测试工况中,为了保护电缆,在试验中设备未完全加载到最终装配位置,因此上述所开展的数值计算结果同时为最后破坏状态提供了预测。

图9 验证试验Fig.9 Validation test

5 结论

以飞行器舱体连接电缆为研究对象,首先基于接触理论建立电缆接触模型以描述内部导线间的接触和摩擦行为,采用数值试验方法模拟径向压缩载荷下的机械特性,并开展试验验证工作,得到如下主要结论:

1)在径向压缩载荷下,绝大多数的内部导线被挤开,电缆受压截面由圆形变为蝴蝶形,表现出一定的流动特征。当内部导线被设备和凸台共同夹住时,产生显著的Mises应力,因此存在机械损伤导致失效的可能。

2)电缆受压位置是影响电缆损伤机械特性的重要因素。计算结果表明当改变电缆时受压位置时,电缆受挤压区域随之改变并决定了最终电缆的变形模式。当相对位置为-4 mm,-2 mm,0 mm,2 mm,4 mm时,导线最大应力分别为177.13 MPa,175.91 MPa,158.26 MPa,183.09 MPa,0 MPa。在数值计算结果的基础上,通过结合装配试验,由此确定了整个电缆挤压最危险工况。

3)文中开展了径向压缩下的连接电缆力学行为研究,定性给出了多种典型装配工况下电缆损伤结果。后续可进一步开展电气性能与机械损伤的关联性研究,构建电缆损伤定量分析方法,为电缆监测与判断提供精确参考。