7-9 岁儿童大肌肉动作发展测验常模的建立

郑雨 顾大成 胡祎（.南宁师范大学师园学院 广西 南宁 506；.南宁师范大学体育与健康学院 广西 南宁 500；.南宁市青秀区埌东小学 广西 南宁 5008）

引言

在不同时期儿童大肌肉动作发展的侧重点也有所不同，8岁是儿童大肌肉动作发展的敏感期，孩子的大肌肉动作模式在这个时期变化是最大的。众多研究表明，儿童大肌肉动作发展熟练度会影响其参与体育活动的积极性，促进其体质健康、体适能水平的提升。相反，大肌肉动作发展出现障碍，会影响儿童的身心健康发展。因此，定期对儿童的大肌肉动作发展水平进行评估和监测是必不可少的。

国外学者经过多年实验的积累，研制出了多种评估儿童动作发展的成熟工具，其中最具有代表性的是美国Ulrich 学者2013 年修订的大肌肉动作发展测验第三版（TGMD-3）。我国部分地区如上海、太原和山东等，建立不同性别、年龄、类型的大肌肉动作发展常模，研究发现各地原始分数差异较大，建立的常模不具有通用性，且广西尚未建立儿童大肌肉动作发展常模。因此，本研究以广西8 所小学7-9 岁儿童为样本，考察TGMD-3 的应用信度、效度，并根据测试的实际得分，建立区域性大肌肉动作发展测验常模，为早期干预提供客观依据，旨在做到“因材施教”，促进儿童心理的健康发展。

1、研究对象与方法

1.1、研究对象

采用简单整群抽样法在广西8 所小学选取1040 名7-9 岁儿童作为受试对象，其中男童565 名，女童475 名。测试前向受试学校负责人、班主任和家长介绍清楚测试目的与意义，并请受试者家长签署知情同意书。

1.2、测量工具

本研究采用大肌肉动作发展测验第三版（TGMD-3）对1040 名（7-9 岁）儿童进行测试，测试内容为移动技能和物体操控技能测两个分测验，其中移动技能内容由跑步、蹦跳、前滑步、立定跳远、单脚跳和侧滑步构成，物体操控技能由原地运球、双手接球、脚踢固定球、肩上投球、下手抛球、双手挥棒击固定球和单手握拍击反弹构成，共13 个动作技能，每个动作技能都被分解成3-5 个不等的标准分，测试对象能正确完成测试项目评分表上的一个动作标准，在评分表上给他打“1”分，不能正确地完成打“0”分，每个动作技能完成两次，两次得分相加为这个动作技能的最后得分。TGMD-3量表总分为100 分，移动技能为46 分，物体操控技能为54 分。

1.3、数理统计法

使用Pearson 相关系数、克隆巴赫α 系数对TGMD-3 的结构信度进行检验，采用探索性因子分析、验证性因子分析对测验量表的效度进行检验，利用双因素方差分析（ANOVA）对年龄、性别和性别×年龄进行差异性分析，应用IBM SPSS 26.0 软件，运用描述性统计分析法对TGMD-3 测试原始数据是否符合正态分布进行检验。

2、结果

2.1、信度检验

（1）评分者信度。

两名评分员独立评分所得分数相关系数（r）越接近1，表明评分者信度就越高，大于0.80 表明较高，等于或大于0.90表明非常高。由表1 可知，大肌肉动作发展的评分者相关系数分别为0.973，P ＜0.01，说明评分者间的评分具有非常高的信度。

表1 不同评分人员评分相关系数（N=120）

（2）同质性信度。

同质性信度主要是使用克隆巴赫α 系数对TGMD-3 同质性信度进行验证,α 系数在0-1 之间,α 越接近1 表示信度越好，0.8-0.9 表示较好。由表2 看出，不同性别的大肌肉动作发展信度系数较好（α=0.859-0.866），总体α 系数为0.860，说明TGMD-3 量表拥有较好的同质性信度。

表2 7-9 岁儿童各动作技能克隆巴赫α 系数（N=1040)

（3）重测信度。

一般认为重测得分相关系数在0.7-0.8 表示具有一定的相关性，0.80-0.9 表示较高，等于或大于0.90 表示非常高。在本研究中，大肌肉动作发展为0.941，P ＜0.01（见表3），表明TGMD-3 量表重测得分有较高的相关性,重测信度较好。

表3 重测相关系数（N=120）

2.2、结构效度检验

本研究先对所选取的样本数据进行因子分析的适应性检验，然后再进行验证性因子分析检验TGMD-3 结构效度。吴明隆给出KMO 和Bartlett 球形检验值的度量标准：KMO 值大于0.90 表示非效度非常好,0.8-0.9 表示效度较好,0.7-0.8 表示效度适合；Bartlett 球形检验P ＜0.05 表明效度有意义。由表4 可知，KMO 值为0.878（KMO ＞0.8），Bartlett 球形检验结果：X2=5191.622，P ＜0.01，说明本研究选取的1040个样本数据适合进行因子分析。

表4 进行因子分析的适应性检验（N=1600）

本研究使用IBM AMOS 26.0 软件检验数据与假设的双因素结构模型的拟合程度，从而验证TGMD-3 的结构效度。通常认为，X2/df ≤3，RMSEA ≤0.05，0.9 ＜CFI、GFI、AGFI、IFI、TLI，各子测试在相应分测验标准化后的因子负荷值大于0.40，表明理论模型与数据拟合较好；X2/df ≤5，RMSEA ≤0.08，0.8CFI、GFI、AGFI、IFI、TLI ＜0.8 可 接受。从表5 可知，X2/df=2.482（X2/df ＜3），CFI=0.849、IFI=0.852、TLI=0.816 大于0.8，GFI=0.960（GFI ＞0.9）、AGFI=0.943（AGFI ＞0.9），RMSE=0.05 小于0.08，标准化后的因子负荷值在0.49-0.80 之间大于0.4。说明本研究建立的TGMD-3 理论模型与所选取的样本数据拟合较好，也验证了TGMD-3 理论结构较好。

表5 TGMD-3 测验拟合度一览表（N=1040）

2.3、7-9 岁儿童大肌肉动作发展特征

本研究以年龄、性别为自变量，大肌肉动作发展为因变量进行双因素方差分析（MANOVA），分析年龄、性别对7-9 岁儿童三个因变量得分的影响差异。结果显示（见表6），大肌肉动作发展得分在年龄、性别上有非常显著差异（P ＜0.01）,在年龄×性别的交互作用上没有显著性差异（P ＞0.05）。

表6 南宁市儿童大肌动作技能发展的双因素方差分析(N=1040)

图1 显示不同年龄男女童的大肌肉动作发展得分情况，可以看出随着年龄的增长儿童大肌肉动作发展、移动技能和物体操控技能均呈上升趋势，不同年龄儿童的大肌肉动作发展（P ＜0.01)，9 岁儿童显著（P ＜0.01)高于7 岁和8 岁儿童，8 岁儿童显著（P ＜0.01)高于7 岁儿童；7-9 岁儿童大肌肉动作发展性别上有非常显著差异（P ＜0.01）。鉴于此，本研究将按性别分组建立大肌肉动作发展测验常模。

图1 不同年龄、性别的7-9 岁儿童大肌肉动作发展得分图

2.4、7-9 岁儿童大肌肉动作发展测验五等级常模的建立

本研究先对7-9 岁儿童的大肌肉动作发展分数进行正态性分布检验，根据表7，发现其峰度和偏度数值在-2-2 之间，说明该年龄段儿童的大肌肉动作发展原始分数服从正态分布。因此，将这些原始分数转换成标准Z 分数，得知标准Z 分数的范围在-3-3 之间，再根据标准Z 分数分层方法，将标准Z分数分为（-3,-2]、(-2,-1]、(-1,1]、(1,2]、（2,3]五层，最后构建不同年龄、性别儿童大肌肉动作发展的五等级常模（见表8）。

表7 南宁市7-9 岁儿童大肌肉动作发展正态分布检验

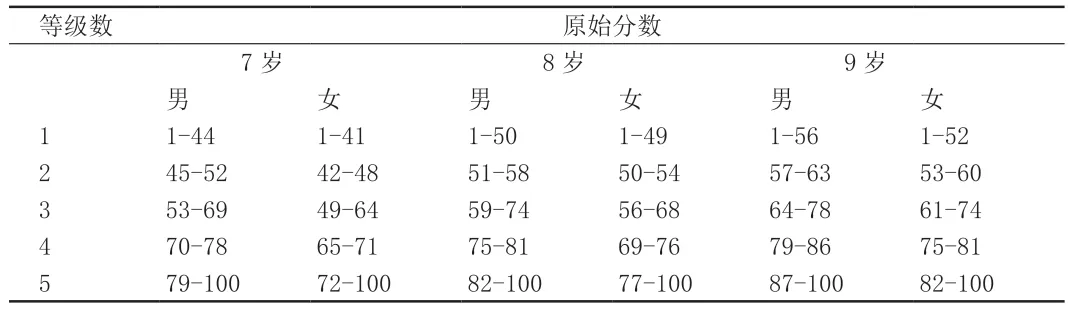
表8 不同性别儿童大肌肉动作发展等级常模

3、讨论

3.1、TGMD-3 量表信度

本研究对大肌肉动作发展的评分者信度、同质性信度和重测信度进行了检验。采用Pearson 相关系数检验两名评分员对同一受试者独立评分所得分数的一致性。在本研究中，大肌肉动作发展的评分者信度大于0.95，刁玉翠的研究结果超过了0.96，表明TGMD-3 量表具有明清晰明确的评分标准。

采用克隆巴赫α 系数对TGMD-3 量表同质性信度进行检验，研究结果表明α 系数大于0.81，具有较高的同质性信度，与李兴盈研究结果一致，说明TGMD-3 对于7-9 岁儿童大肌肉动作发展评估具有较好的适用性。

根据重测信度的结果，第一次测试和第二次测试测的分数之间呈显著相关。此外，第一次测试和第二次测试测之间的大肌肉动作发展高度正相关，表明该量表测试结果在时间跨度上具有较好的稳定性水平。

3.2、TGMD-3 量表效度

在运用验证因子分析检验结构效度的过程中，所选取的样本数据能否进行因子分析是研究中必须注意的问题。因子分析的结果与样本量密切相关，Hair 等人建议做因子分析应满足以下三个要求。第一，测试项目数量与受试者的比例至少是1:10；第二，样本量不小于100；第三，KMO 值大于0.5。TGMD-3 包含13 个测试项目，本研究的样本量为1040，比值为1:80，KMO 值为0.897 ＞0.5，因此研究所选取的样本量适合做因子分析。采用验证性因子分析对TGMD-3 的结构效度进行验证，研究结果表明所有拟合指数都是可接受的，说明本研究建立的TGMD-3 双因素模型与所选取的样本数据拟合较好，验证了TGMD-3 理论结构较好，这与Estevan、Valentini 等人的研究结果一致。此外，Wagner 使用单因素模型、Mohammadi 使用单因素模型和双因素模型对TGMD-3 的结构效度进行检验，发现模型的拟合指数较好，表明该量表跨文化同样具有较好的结构效度。

3.3、7-9 岁儿童大肌肉动作发展特征

在本研究中，7-9 岁儿童大肌肉动作发展随着年龄的增长呈上升趋势，且各相近年龄段动作技能熟练度存在显著差异，这与国内外学者研究结果一致。符合Seefeldt 的动作发展金字塔模型理论来阐述人类动作技能发展规律特征。儿童的动作技能熟练水平不是自然形成的，必须通过被教授、学习、不断地练习和强化才能熟练掌握这些动作技能，随着时间的推移而稳定下来，这也可能是随着年龄的增长各动作技能得分高的原因。

4、结论

（1）TGMD-3 测评工具有较好的难度、区分度、信度和效度；

（2）7-9 岁儿童的大肌肉动作发展在年龄上存在差异，在性别上存在差异，移动技能无性别差异。7、8、9 岁组男童的大肌肉动作发展得分显著高于女童；

（3）按年龄、性别分组建立大肌肉动作发展测验五等级等常模。