地球静止轨道航天器绕飞持续观测任务轨迹规划与控制

张海涛,王伟林,张雅声,王 浩,李 智*

(1. 航天工程大学, 北京 101416; 2. 酒泉卫星发射中心, 甘肃 酒泉 735000)

由于地球静止轨道(geosynchronous orbit, GEO)的轨道优势,许多高价值航天器都位于GEO区域。2021年,欧洲航天局空间碎片办公室在《欧洲年度空间环境报告》中指出,截至2020年底,共有873个GEO空间目标[1]。GEO空间目标距离地面近36 000 km,给地面高清观测[2-3]带来巨大挑战。

GEO区域的成像卫星能够在不受大气干扰的情况下,拍摄更清晰的GEO空间目标图像,并能更好地监测GEO航天器的工作状态。因此,部署成像卫星接近GEO航天器,实现对GEO航天器的持续观测具有重要意义。利用GEO的轨道周期特点,成像卫星可以在整个自然绕飞任务中以良好的观测角对GEO航天器进行连续观测。

根据用于表示相对运动的状态量的类型,研究相对运动的模型可以分为两类:第一类是用轨道参数作为状态量的相对运动模型;第二类是用相对状态矢量作为状态量的相对运动模型,例如用直角坐标系中的相对位置和速度[4]作为状态矢量。第一类模型[5-8]的优点是易于分析摄动对相对运动的影响。因此,这种模型具有较高的精度,并能有效避免偏差的长期累积。这种模型的缺点是不便于建立状态微分方程,不利于研究连续小推力作用下的相对运动。在第二类模型[9-11]中,Clohessy-Wiltshire (CW)方程应用最为广泛,CW方程的优点在于:建立状态方程后,便于结合最优控制理论开展成像卫星接近GEO航天器的研究,也便于对飞行编队进行研究。缺点是CW方程的偏差较大,且偏差随时间不断累积[12]。

在绕飞轨迹规划问题上,刘猛等[13]给出了航天器基于最小冲量进入对空间目标绕飞轨道的策略,在轨道机动燃料消耗方面有借鉴价值。黄艺等[14]研究了对非合作目标绕飞任务的姿轨耦合控制策略,给出能够对外界干扰和不确定参数具有很好抑制效果的控制方案。谭天乐等[15-17]给出近圆轨道和大椭圆轨道的相对运动建模和解析方法,提供了对空间非合作目标高精度的相对悬停和循迹绕飞控制方法。刘涛等[18]提出一种用于非合作目标惯性指向轴位置捕获的绕飞方法。常燕等[19]研究了对椭圆轨道上非合作目标进行长期绕飞检测的相对运动轨道构型设计与构型保持问题。梁静静等[20]基于粒子群算法研究了双脉冲绕飞的优化问题和安全绕飞轨迹设计问题。王功波等[21]在连续小推力条件下,针对圆轨道推导了满足快速绕飞条件的空间圆编队动力学模型。Dang[22-23]推导了在任意开普勒轨道上相对运动的新状态转换矩阵,给出了Tschauner-Hempel(TH)方程的解。

在CW方程的偏差问题上,通过修正CW方程的非球形摄动偏差和非线性二次项偏差改进CW方程;在轨迹规划问题上,计算对GEO航天器绕飞的初始相位区间,成像卫星在连续小推力作用下接近GEO航天器,以合适的初始相位对其开始绕飞,实现对GEO航天器的自然绕飞并持续以有利的光照条件对其观测,如图1所示。

图1 成像卫星P在整个绕飞任务中以良好的观测角对GEO航天器E进行拍照Fig.1 The optical satellite P can take pictures of the GEO spacecraft E with favorable observation angles throughout the entire fly-around mission

1 CW方程

CW方程采用当地垂直当地水平(local vertical local horizontal, LVLH)坐标系,该坐标系以航天器质心为原点,x轴沿地心到航天器质心的方向;z轴垂直于轨道平面,与瞬时角动量方向相同,y轴方向根据右手定则确定。

两个非常接近的航天器分别记为M和S,M为主航天器,S为辅航天器,存在:

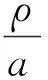
(1)

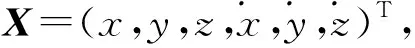
(2)

式中:

(3)

(4)

其中,ω为航天器M的轨道角速度。

记t0时刻,S的相对状态矢量为X(t0),则t时刻,航天器S的相对状态矢量为:

(5)

式中:

(6)

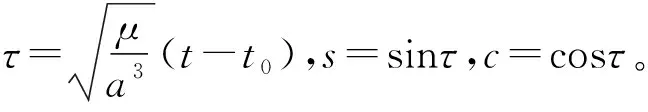
2 改进的CW方程

非线性、参考轨道的偏心率和摄动是CW方程偏差的三个来源。在成像卫星对GEO航天器的接近和绕飞的任务中,以GEO航天器为原点建立LVLH坐标系,则CW方程偏差来源主要为非线性项和摄动项。记P为成像卫星,E为被成像的GEO航天器。已知P和E的初始轨道参数,改进的CW(improved CW, ICW)方程研究相对运动的步骤如下:

步骤1：以航天器E的质心为原点建立LVLH坐标系,记为R;

步骤2：计算成像卫星P的初始状态矢量,即在LVLH坐标系中成像卫星P相对GEO航天器E的位置和速度矢量:

(7)

据文献[22]的方法可求得:

(8)

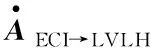
步骤3：GEO航天器受到的主要摄动为非球形、三体和太阳光压摄动。然而,由于GEO轨道的轨道特性,非球形摄动是导致两航天器存在相对运动偏差的最主要因素。考虑J2和J22项摄动,将CW方程中的万有引力常数μ修正为ICW方程中的万有引力常数μ′:

(9)

式中,μ=3.986 005×1014m3/s2为万有引力常数,rE为地球的赤道半径,ac为GEO轨道的半长轴,λ为GEO航天器E的星下点地理经度,J2=-1.082 627×10-3,J22=1.815 528×10-6。

步骤4：通过对CW方程初始状态矢量的修正来补偿非线性长期项偏差。将非线性二次项假设为虚加的摄动,通过虚摄动解可求解对CW方程初始状态矢量的修正项。对CW方程初始状态矢量的修正项为:

(10)

式中,nL为LVLH坐标系相对ECI坐标系的旋转角速度,ρ2为成像卫星P与航天器E的相对距离的平方,β0为初始时刻y轴沿z轴反方向到成像卫星P位置矢量的角度。

步骤5：将两个独立的修正结合起来,以补偿非线性偏差和非球形摄动偏差。ICW方程的初始状态矢量为:

(11)

在ICW方程中,通过步骤3补偿非球形摄动偏差,通过步骤4补偿非线性偏差,2.1节和2.2节分别研究步骤3和步骤4补偿摄动偏差和非线性偏差的原理。

2.1 补偿非球形摄动偏差

定义航天器在离地球无限远处的重力势能为0。r为ECI坐标系中的位置矢量,r为位置矢量的大小。设r处单位质量的重力势能为:

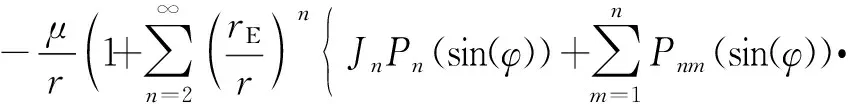
(12)

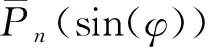
(13)

化简后,引力势为:

各项的权重为:

(15)

对于GEO航天器,权量最大的五项分别是J2,J22,J3,J31和J33,权重比为:

A2∶A22∶A3∶A31∶A33=11 053 ∶64 ∶3 ∶7 ∶6

(16)

因此,J2和J22是非球形摄动中权重最大的项。将这两项引入ICW方程中,包含J2和J22项的引力势为:

(17)

式中,λ22=-14.929°。对于两个相对接近的GEO航天器,其星下点的地理经度近似相等。由于sin2φ≈0,cos2φ≈1,式(17)可简化为:

(18)

J2和J22对相对运动的影响体现在与CW方程相比,ICW方程中的万有引力常数修正为:

(19)

2.2 补偿非线性偏差

在CW方程中,为了得到线性的状态方程,重力加速度的泰勒级数展开式中的非线性项在式(1)的条件下被舍弃,二次项是偏差的主要来源。被舍弃的二次项在位置分量上产生常数项、长期项和短周期项三种类型的偏差。长期项只出现在y轴方向上,是对精度影响最大的偏差。偏差的长期项可通过对CW方程的初始状态矢量的修正来补偿,利用摄动法可计算用于补偿CW方程中非线性偏差的修正项。摄动法中,将非线性二次项作为CW方程中的虚加摄动力。通过虚摄动解求解用于补偿CW方程中非线性长期项偏差的初始状态矢量的修正项。

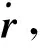
(20)

其中,R为在r处单位质量的势能。成像卫星P相对GEO航天器E的位置矢量为ρ=rP-rc。根据式(12),对于航天器E和成像卫星P,存在:

(21)

(22)

其中,fc和fP分别为航天器E和成像卫星P受到的摄动力,如太阳光压摄动等。式(21)与式(22)相减得:

(23)

式中,Δf为成像卫星P和航天器E受到的摄动偏差。ICW方程在步骤3中对主要摄动偏差进行修正,在步骤4中对非线性偏差进行修正。因此,在修正非线性偏差时,令Δf=0。将式(23)从ECI坐标系转换到LVLH坐标系:

(24)

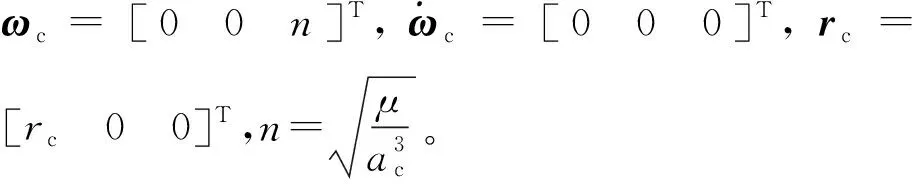
(25)

在CW方程中,式(25)可化简为:

(26)

记CW方程中的状态矢量为:

(27)

解为:

(28)

保留式(25)等号右边的二次项,舍弃高阶项。将式(25)化简为:

(29)

根据式(29),将重力加速度泰勒级数展开式中的非线性二次项作为CW方程中虚加的摄动力,虚加摄动力为:

(30)

将式(29)简记为:

(31)

式(31)为CW方程的非线性偏差传播方程。记CW方程的非线性偏差为:

(32)

根据式(5)可得式(31)的解为:

(33)

CW方程中被舍弃的二次项导致y轴方向偏差的长期项为:

(34)

为了修正y轴方向偏差的长期项,令ynl-long=0,可得非线性偏差的零累积准则:

(35)

因此,根据虚摄动解可得到对CW方程初始状态矢量的修正项如式(10)所示。

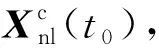
2.3 偏差修正验证

为了研究ICW方程相对CW方程的改进效果,选取成像卫星P和GEO航天器E进行仿真验证,其轨道半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角w、平近地点角m如表1所示。

表1 成像卫星P与GEO航天器E的轨道参数

LVLH坐标系中成像卫星P的初始状态矢量如表2所示。初始时刻从y轴沿z轴反方向到成像卫星P的位置矢量的角度为0°,X为CW方程的初始状态矢量,Y为ICW方程的初始状态矢量。

表2 成像卫星P的初始状态矢量

2.3.1 非球形摄动偏差修正验证

为了验证ICW方程中步骤3的非球形摄动解,将非球形摄动解与高精度轨道传播(high-precision orbit propagator, HPOP)模型作对比。HPOP模型中考虑前21阶非球形摄动、太阳光压摄动和三体引力摄动。利用二体模型、HPOP模型和步骤3中的非球形摄动解,分别在ECI坐标系中计算成像卫星P和GEO航天器E的位置。将P在ECI坐标系中的位置分别转换到LVLH坐标系R中,P在R中的位置即为P相对于E的位置,将HPOP模型得到的相对位置视为真实相对位置。在仿真场景中,航天器星下点的地理经度为165″E。

相比二体模型,非球形摄动解在相对位置的x、y和z方向对精度的提高分别如图2、图3和图4所示。图中红色实线表示非球形摄动解相对HPOP模型的偏差,蓝色虚线表示二体模型相对HPOP模型的偏差。通过比较可得,非球形摄动是摄动偏差的最主要因素,非球形摄动解提高了CW方程在LVLH坐标系x、y轴方向的精度。

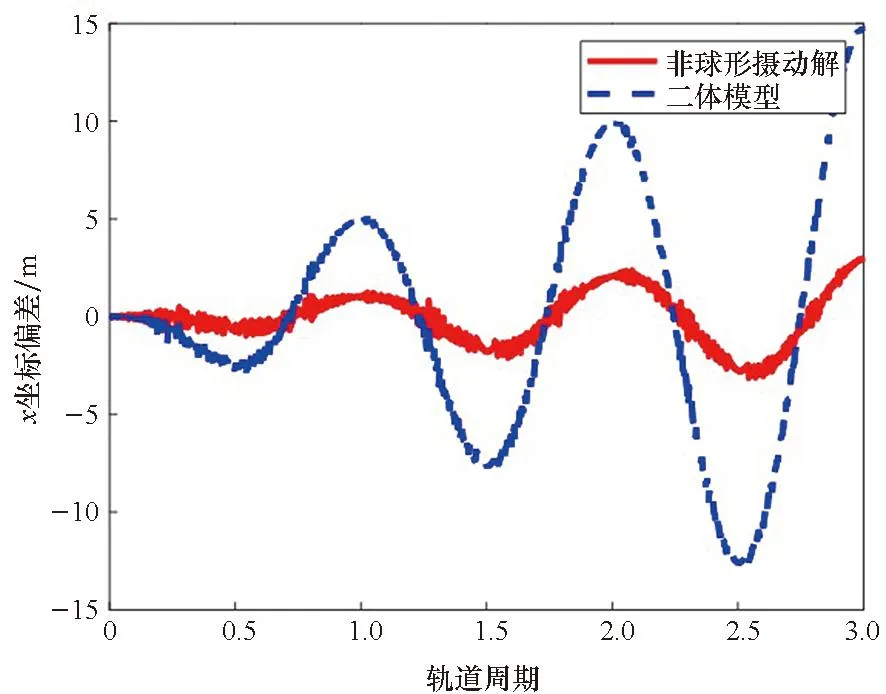
图2 非球形摄动解对x方向精度的提高Fig.2 Improvement of the non-spherical perturbation solution in x-coordinate

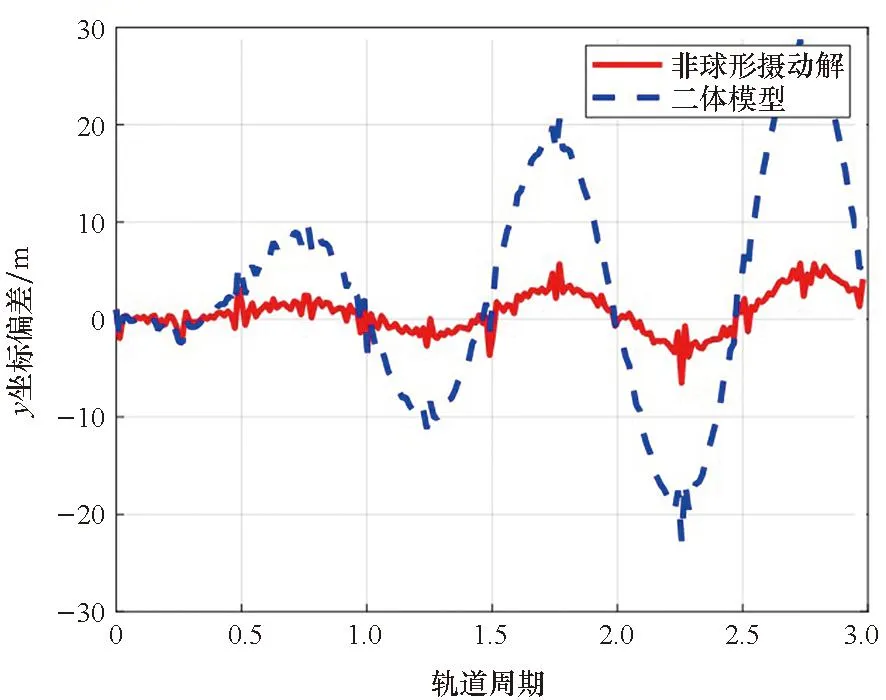
图3 非球形摄动解对y方向精度的提高Fig.3 Improvement of the non-spherical perturbation solution in y-coordinate

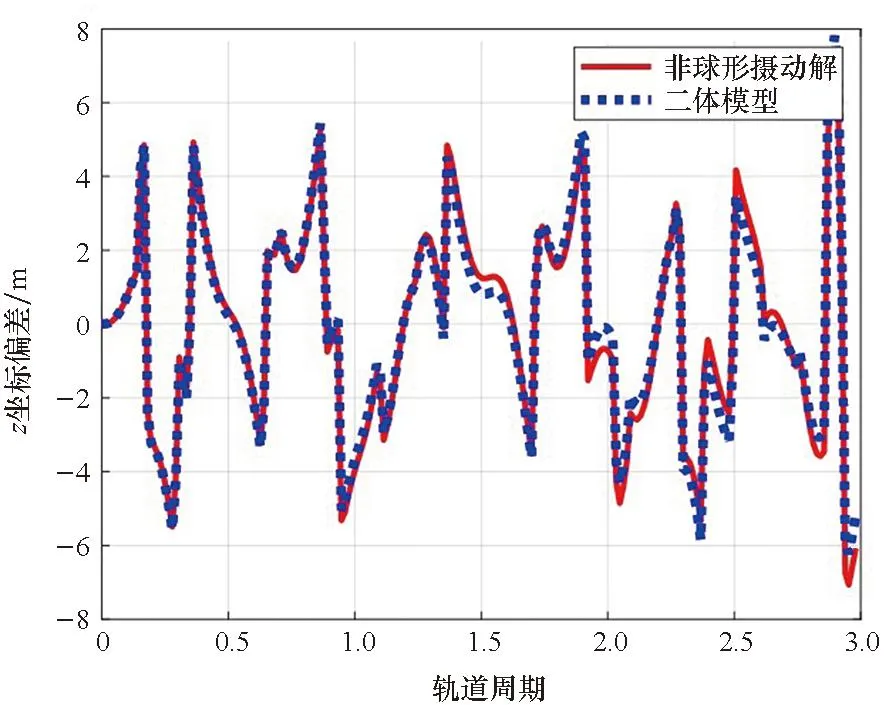
图4 非球形摄动解对z方向精度的提高Fig.4 Improvement of the non-spherical perturbation solution in z-coordinate

利用ICW方程和CW方程仿真成像卫星P相对于GEO航天器E的运动,比较三个轨道周期内相对位置的x、y、z坐标差异。由于CW方程存在非线性偏差,为了展现ICW方程中步骤3对CW方程的改进效果,本节中不对ICW方程进行非线性偏差修正。ICW方程与CW方程中相对位置的x、y、z坐标差值分别如图5、图6和图7所示。

图5 ICW方程和CW方程在x轴方向的差值Fig.5 Deviation in x-coordinate between ICW equations and CW equations

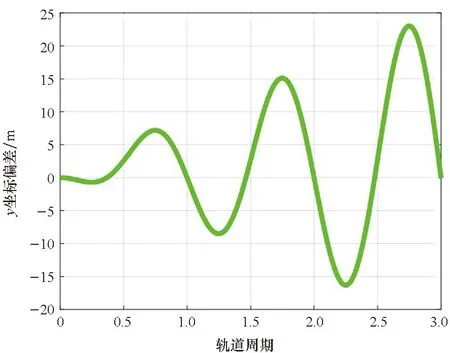
图6 ICW方程和CW方程在y轴方向的差值Fig.6 Deviation in y-coordinate between ICW equations and CW equations

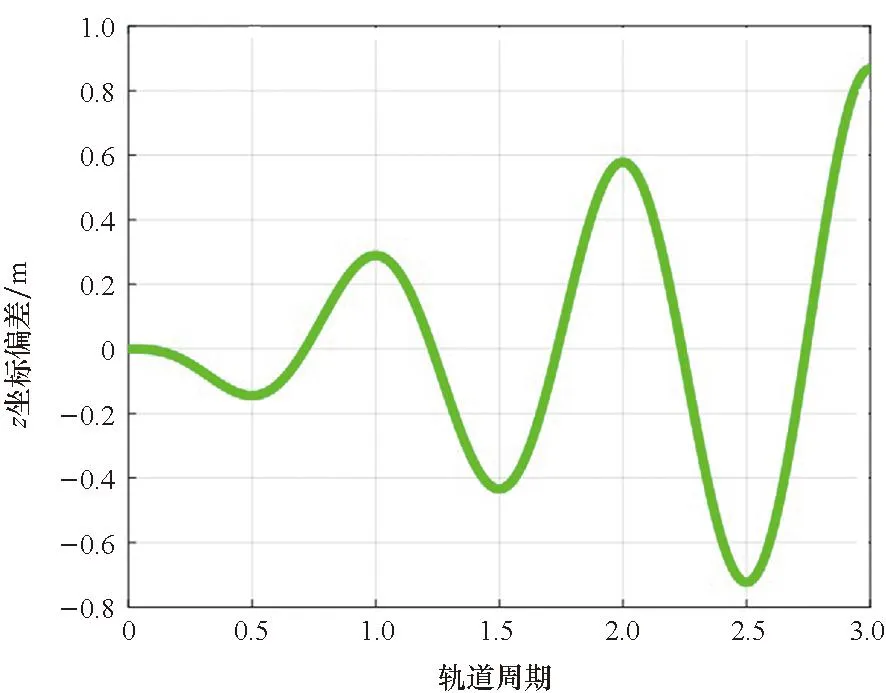
图7 ICW方程和CW方程在z轴方向的差值Fig.7 Deviation in z-coordinate between ICW equations and CW equations

从图5～7中可以看出,ICW方程与CW方程中相对位置的x、y、z坐标差值呈周期性变化,且差值幅值逐渐增大。x、y坐标差值幅值的增长率在同一个数量级,z坐标幅值的增长率比x、y坐标幅值的增长率小一个数量级。

2.3.2 非线性偏差修正验证

CW方程和ICW方程计算出的成像卫星P相对GEO航天器E的位置的y坐标如图8所示。图中红色实线代表ICW方程的y坐标,蓝色虚线代表CW方程的y坐标。ICW方程与CW方程的y坐标差值如图9所示。

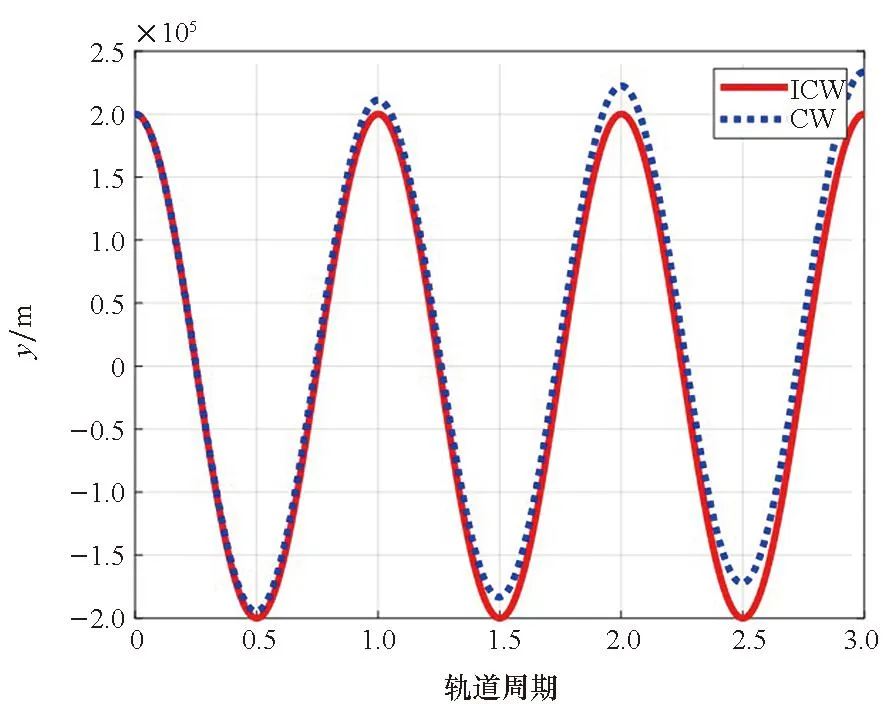
图8 ICW方程和CW方程中的y坐标值Fig.8 y-coordinate in ICW equations and CW equations

图9 ICW方程和CW方程在y轴方向的 非线性偏差值Fig.9 y-coordinate nonlinear deviation between ICW equations and CW equations

为了验证ICW方程步骤4的改进效果,将CW方程和ICW方程计算的相对位置的y坐标与真值进行比较。由于CW方程存在摄动偏差,为了展现ICW方程中步骤4对CW方程的改进效果,本节不对ICW方程进行摄动偏差修正。如图10所示,红色实线表示ICW方程中相对位置的y坐标与真值的差值,蓝色虚线表示CW方程中相对位置的y坐标与真值的差值。

图10 ICW方程和CW方程在y轴方向与真值的差值Fig.10 y-coordinate deviation of ICW equations and CW equations from the truth value

成像卫星P与GEO航天器E的初始距离为200 km,3个轨道周期后,ICW方程中相对位置的y坐标相对真值出现36 m的长期偏差,而CW方程的长期累积偏差为33 563 m。ICW方程的长期偏差仅约为CW方程的0.1%。通过比较,验证了ICW方程对非线性偏差长期项补偿的有效性。

ICW方程补偿了相对位置y轴方向二次非线性偏差的长期项和x、y轴方向上主要的摄动偏差。ICW方程中,在建立状态微分方程时,不对非线性偏差的短期项进行修正。在有更高的精度需求时,可用短期项偏差修正结果状态矢量。这样处理的优点在于:得到的控制系统是线性时不变系统,同时在最终的状态矢量中加入短周期项可保证结果的准确性。

3 轨迹规划

对GEO航天器绕飞持续观测任务的轨迹规划分为两段:成像卫星抵近GEO航天器和成像卫星对GEO航天器绕飞。为了实现燃料消耗最少,成像卫星最理想的轨迹规划方案是:在连续小推力控制下接近GEO航天器,然后对GEO航天器自然绕飞完成持续观测任务。

3.1 成像卫星对GEO航天器绕飞

3.1.1 观测角和太阳的运动

观测角定义如图11所示。定义α为成像卫星对GEO航天器的观测角。0°观测角表示:成像卫星、GEO航天器和太阳共线,成像卫星处于中间位置。显然,越接近0°,成像卫星对GEO航天器的观测越有利;越接近180°,成像卫星对GEO航天器的观测越不利。成像卫星为了在整个绕飞阶段都能对GEO航天器成像,需观测角始终小于60°。成像卫星能较好地对GEO航天器成像的观测角的最大值取决于成像卫星相机的成像能力和GEO航天器的材质,通常情况下,成像卫星在观测角小于60°的情况下,可实现对GEO航天器成像。

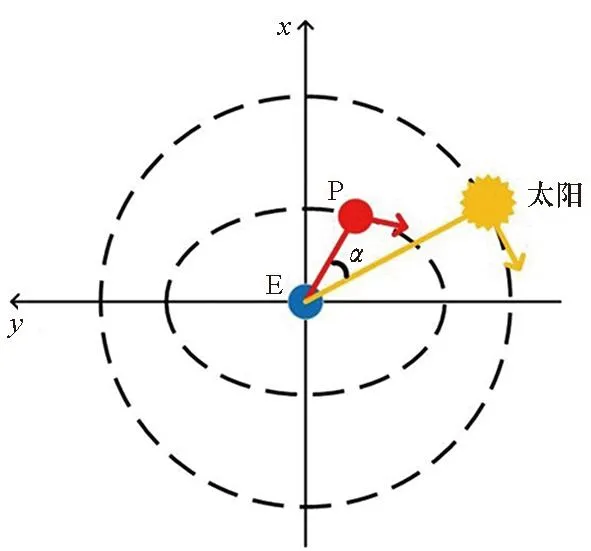
图11 观测角的定义Fig.11 Observation angle

在ECI坐标系中,太阳的轨道参数为:

(36)

其中,T为儒略世纪,d为儒略日。据太阳的轨道参数,可得太阳在ECI坐标系中的位置矢量。由于太阳到地心的距离远大于GEO航天器到地心的距离,假设地心到太阳的方向与GEO航天器E到太阳的方向重合。太阳在以航天器E为原点的LVLH坐标系R中的方向矢量为:

dsun=AECI→LVLH·kECI

(37)

式中,kECI为太阳在ECI中的方向矢量。

3.1.2 绕飞阶段的观测角

设计成像卫星P在GEO航天器E轨道平面内的绕飞轨迹。设tp时刻太阳方向矢量在LVLH坐标系R的xoy平面上的投影与x轴重合,成像卫星P在t0到tp时刻完成对航天器E的抵近,从tp时刻开始绕飞。dP为航天器E到成像卫星P的位置矢量,记θxy为dP在tp时刻的初始相位角,即θxy为tp时刻x轴沿z轴反方向到dP矢量的角度,如图12所示。δ为太阳的赤纬,即太阳的星下点纬度,显然δ∈(-23°26′,+23°26′)。t时刻,dP在LVLH坐标系R中的x、y、z坐标为:

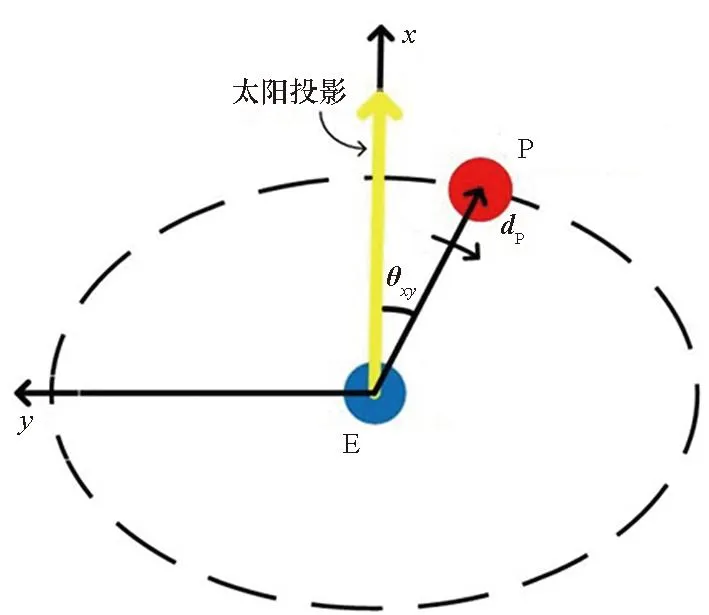
图12 太阳和成像卫星的相对位置Fig.12 Position of the sun and the optical satellite

dP=[x(t),y(t),z(t)]

(38)

(39)

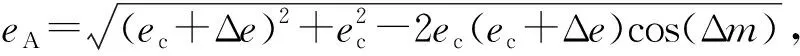
(40)

当θxy=0°时,成像卫星P在GEO航天器E的一个轨道周期内对E的观测角如图13所示。

图13 在θxy=0°时成像卫星P对GEO航天器E的观测角Fig.13 Observation angles of the optical satellite P to the GEO spacecraft E when θxy=0°

太阳的赤纬在-23°26′到+23°26′间变化。记αm为一个轨道周期内P对E的最大观测角,αm随太阳赤纬而变化,如图14所示。当θxy=0°时,αm在δ=0°时取得最小值19.47°,在δ=±23°26′时取得最大值26.35°。因此,成像卫星P在tp时刻以θxy=0开始对GEO航天器E绕飞,成像卫星P对GEO航天器E的观测角始终小于26.35°。

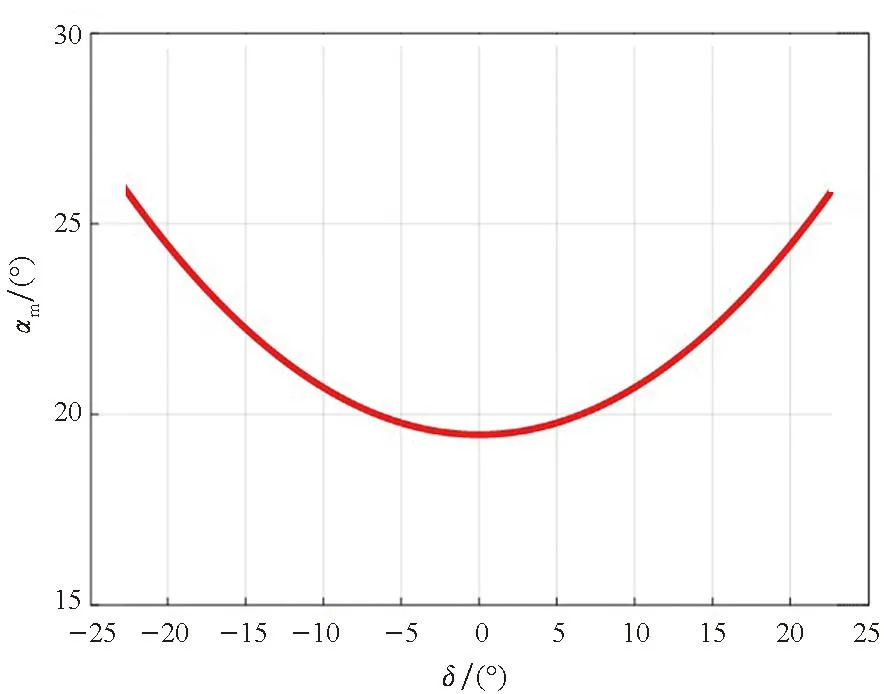
图14 成像卫星P对GEO航天器E的最大 观测角随太阳赤纬的变化Fig.14 Maximum observation angle of the optical satellite P to the GEO spacecraft E varies with the declination of the sun δ

tp时刻,成像卫星P以初始相位角θxy≠0°开始对GEO航天器E绕飞。θxy取不同值时,一个轨道周期内的最大观测角αm随太阳赤纬δ变化,如图15所示。因此,无论太阳的赤纬δ取何值,如果绕飞的初始相位θxy∈(-37.2°,37.2°),在整个绕飞任务中,P对E的观测角始终小于60°,P可以以有利的观测角对E拍照。因此,可对GEO航天器持续观测的成像卫星的绕飞初始相位角区间为θxy∈(-37.2°,37.2°)。

图15 不同θxy时最大观测角αm随太阳赤纬的变化Fig.15 The maximum observation angle in an orbital period αm varies with the declination of the sun δ at different θxy

3.1.3 绕飞轨道参数确定

设计成像卫星P在GEO航天器E轨道平面内的绕飞。在LVLH坐标系R中,绕飞相对轨迹为椭圆,记rxy为相对轨迹的半长轴,记yoff为椭圆相对轨道的中心与航天器E的距离。记Δe、Δi、ΔΩ、Δω和Δm为P与E轨道的偏心率、轨道倾角、升交点赤经、近地点幅角和平近地点角差值:

(41)

已知GEO航天器E的轨道参数,根据任务要求的rxy、θxy和yoff,设计成像卫星P的相对轨迹。根据式(41)可得Δa、Δe、Δi、ΔΩ、Δω、Δm,进而可得成像卫星P在tp时刻的轨道参数。

3.2 成像卫星抵近GEO航天器

据3.1节的方法,可得成像卫星P在tp时刻的轨道参数,已知成像卫星在t0时刻的轨道参数。以成像卫星P的燃料消耗为优化指标,计算成像卫星接近GEO航天器的控制策略,从t0到tp的轨迹优化是一个两点边界问题。状态方程为:

(42)

支付函数为:

(43)

根据式(43),哈密顿函数可写为:

(44)

式中,λ是协态变量。

根据最优化的必要条件,协态方程为:

(45)

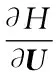
(46)

把式(46)代入式(42),得:

(47)

据式(47)和式(45),可得:

(48)

式(48)的解析解为:

(49)

式(49)可写为:

(50)

已知ICW方程中的初始状态矢量Y(t0)和终端状态矢量Y(tp),可得:

λ*(t0)=Π12(tp)-1[Y*(tp)-Π11(tp)Y(t0)]

(51)

根据式(46)、式(50)和式(51),可得最优控制策略:

U*(t)=-BT[Π21(t)Y(t0)+Π22(t)λ*(t0)]

(52)

4 仿真

从t0到tp,成像卫星P在连续小推力的作用下接近GEO航天器E;自tp时刻开始,成像卫星P对GEO航天器自然绕飞。成像卫星P的相对绕飞轨迹在GEO航天器E的轨道平面内,椭圆相对轨迹的半长轴为20 km,初始相位角θxy=0°。在该场景中,t0为GEO航天器星下点当地时间2021年6月10日00:00:00,tp为2021年6月11日12:00:00。成像卫星P和GEO航天器E在t0时刻的轨道参数如表1所示。

根据CW方程和ICW方程,LVLH坐标系R中成像卫星P在t0和tp时的状态矢量如表3所示,X为CW方程的状态矢量,Y为ICW方程的状态矢量。

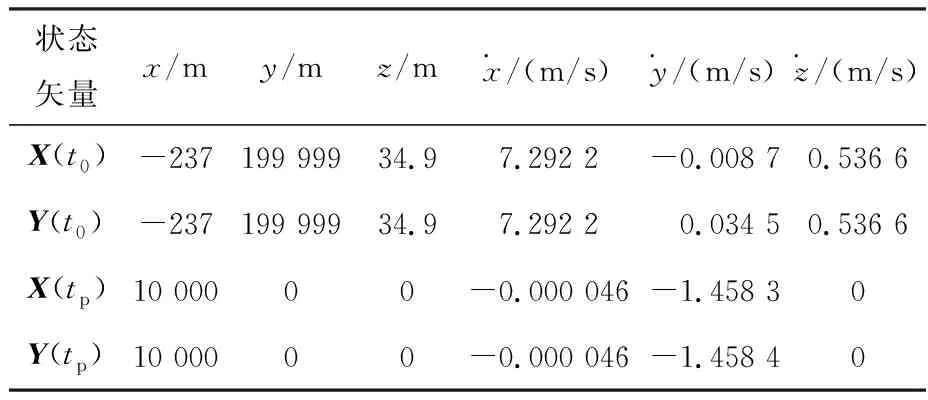
表3 成像卫星P在LVLH坐标系中的状态矢量

分别基于CW方程和ICW方程进行仿真。计算成像卫星P的最优控制策略,将成像卫星P在ECI坐标系中的运动方程积分得到其位置和速度,再将ECI中得到的位置转换到LVLH坐标系中。积分采用龙格-库塔法,积分得到的结果作为成像卫星P的真实位置,进而可得成像卫星P相对GEO航天器E的位置以及P对E绕飞过程中的观测角。将基于CW方程和ICW方程得到的相对位置和观测角进行对比。

4.1 基于CW方程的仿真

基于CW方程进行仿真。t0到tp时间内,成像卫星P在连续小推力作用下接近GEO航天器E,施加的总速度增量为4.70 m/s。图16为成像卫星P相对GEO航天器E的位置在LVLH坐标系xoy平面中的投影。由于CW方程存在偏差,相对绕飞轨迹的中心在y轴方向上偏离GEO航天器E。图17为P到E的距离,tp时刻,P到E的距离不是预先规划的10 km,而是14 km。图18为成像卫星P在tp后的一个轨道周期内对GEO航天器E的观测角,最大观测角为75.57°,成像观测仿真任务失败。

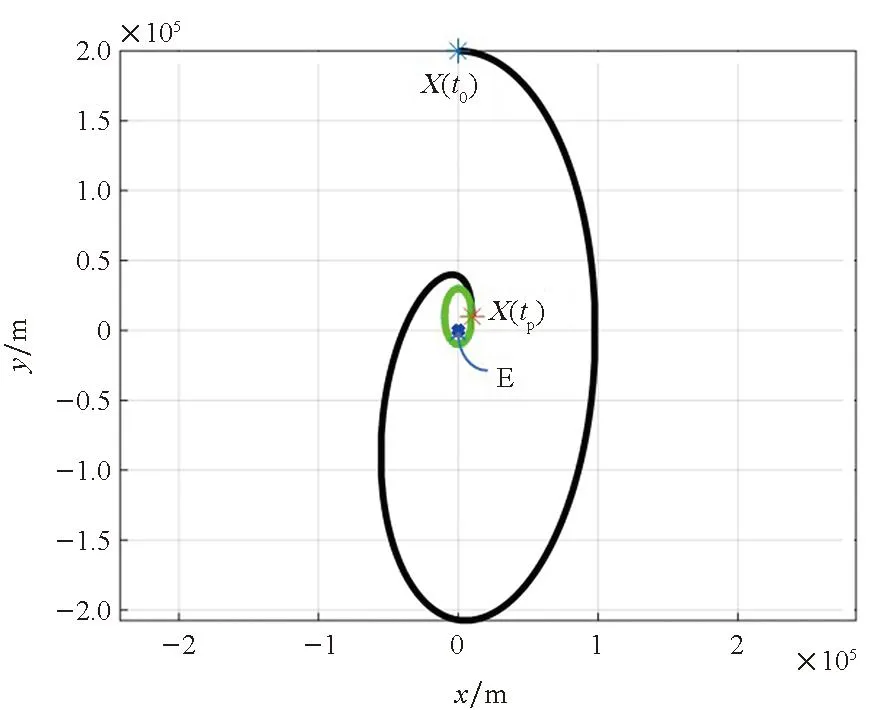
图16 基于CW方程仿真的成像卫星P相对GEO 航天器E的位置在LVLH坐标系xoy平面中的投影Fig.16 Position of the optical satellite P relative to the GEO spacecraft E on the xoy plane based on CW equations simulation

图17 基于CW方程仿真的成像卫星P与 GEO航天器E的距离Fig.17 Distance between the optical satellite P and the GEO spacecraft E, simulation based on CW equations

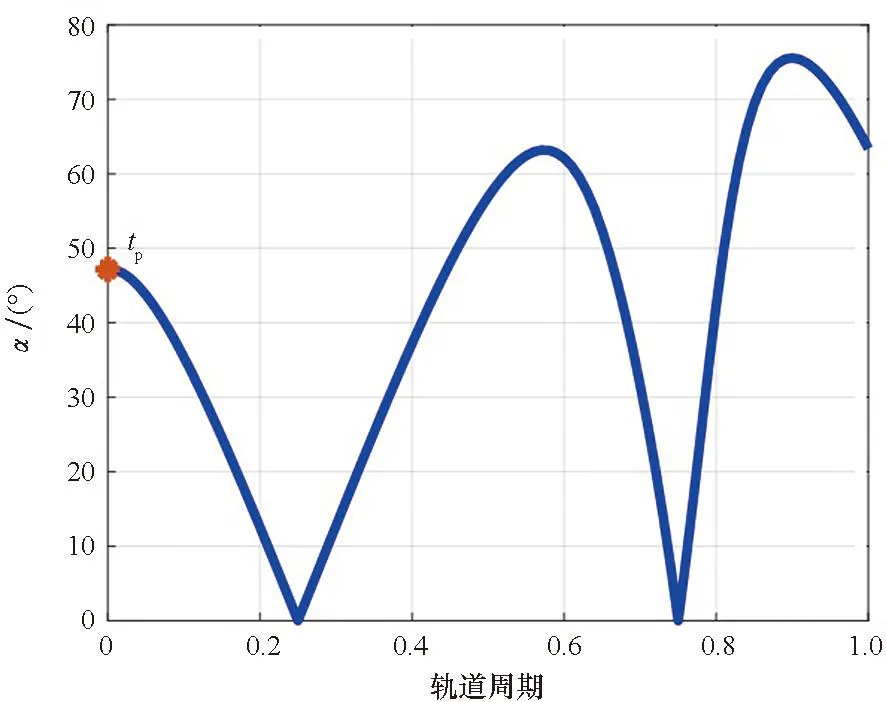
图18 基于CW方程仿真的成像卫星P对 GEO航天器E的观测角Fig.18 Observation angles of the optical satellite P to the GEO spacecraft E based on CW equations simulation

4.2 基于ICW方程的仿真

基于ICW方程进行仿真,图19为成像卫星P从t0到tp的控制推力加速度(工程上一般表述为控制推力),总速度增量为4.67 m/s。图20～22分别表示成像卫星P的推力控制的x、y、z坐标分量。图23为P相对于E的位置,图24为P与E间的距离,tp时刻P与E的距离为10 km,P开始对E自然绕飞。图25为P对E在tp后一个轨道周期内的观测角,最大观测角为22.6°。成像卫星P能以良好的观测角在整个绕飞任务中对GEO航天器E成像。

图19 基于ICW方程仿真的成像卫星P的控制推力Fig.19 Thrust control of the optical satellite P based on ICW equations simulation

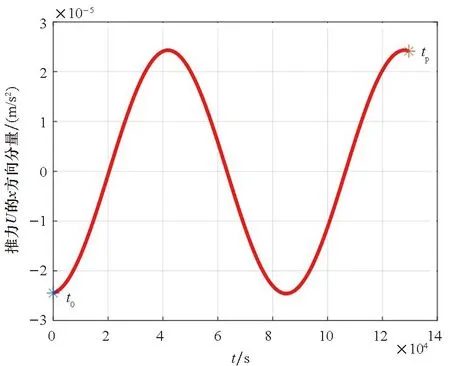
图20 基于ICW方程仿真的成像卫星P在x方向的推力Fig.20 Thrust control of the optical satellite P in x-coordinate simulation based on ICW equations

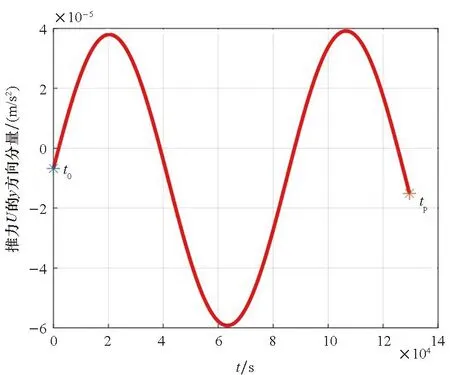
图21 基于ICW方程仿真的成像卫星P在y方向的推力Fig.21 Thrust control of the optical satellite P in y-coordinate simulation based on ICW equations

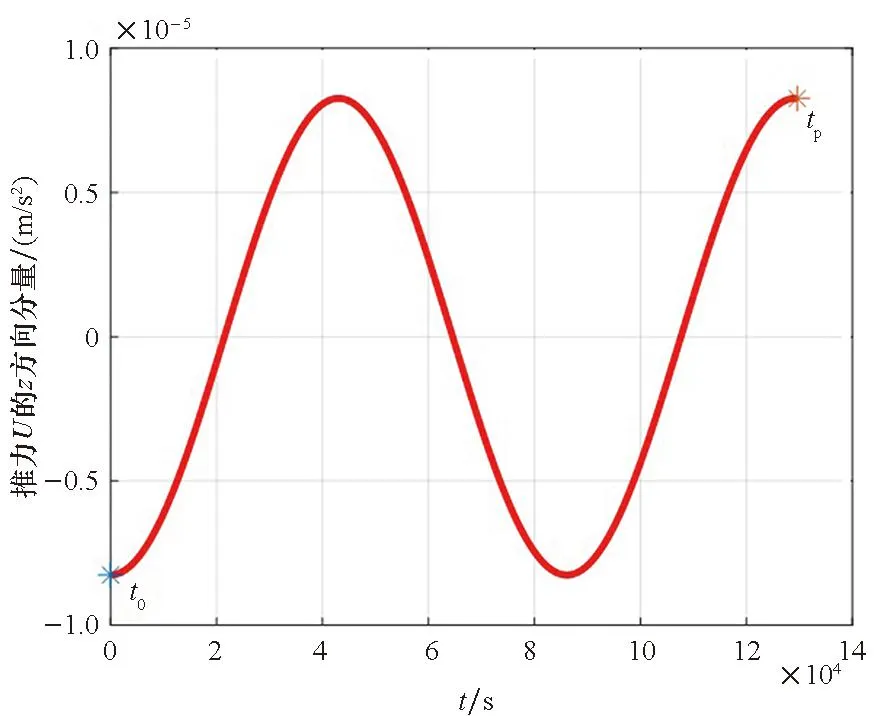
图22 基于ICW方程仿真的成像卫星P在z方向的推力Fig.22 Thrust control of the optical satellite P in z-coordinate simulation based on ICW equations

图23 基于ICW方程仿真的成像卫星P相对 GEO航天器E的位置Fig.23 Position of the optical satellite P relative to the GEO spacecraft E based on ICW equations simulation

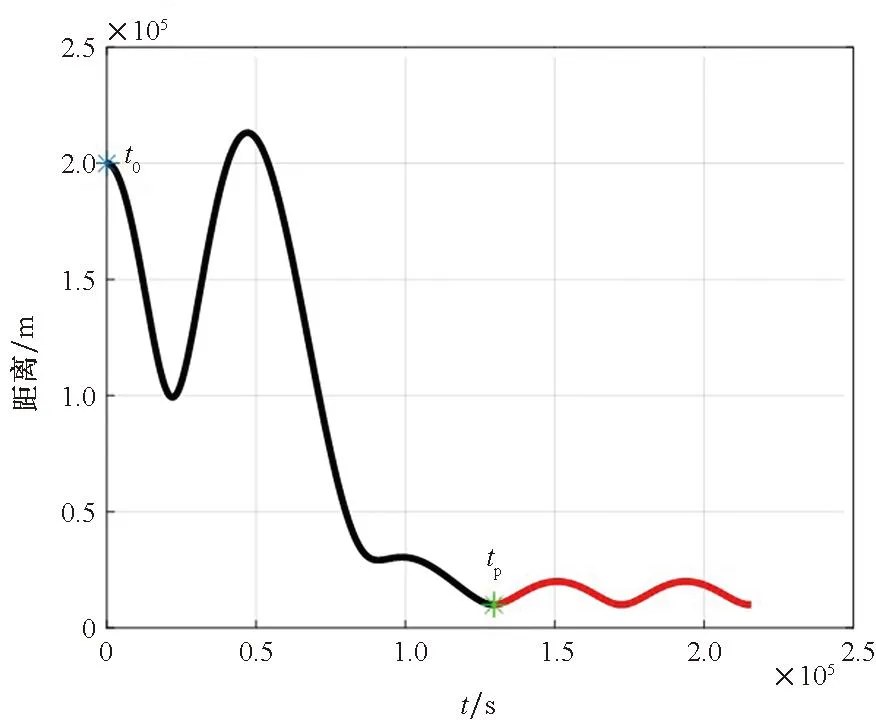
图24 基于ICW方程仿真的成像卫星P与 GEO航天器E间的距离Fig.24 Distance between the optical satellite P and the GEO spacecraft E based on ICW equations simulation

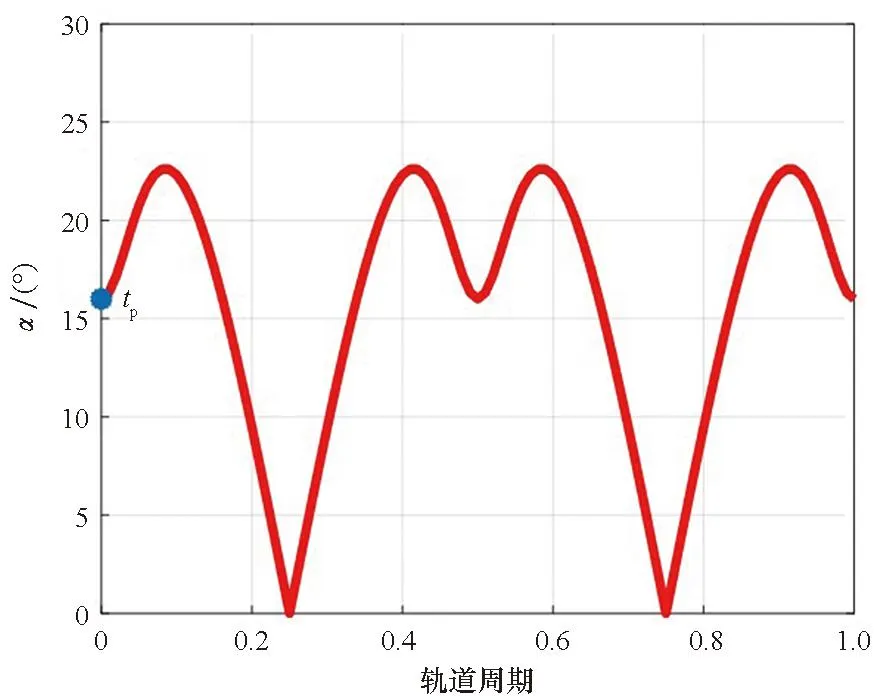
图25 基于ICW方程仿真的成像卫星P对 GEO航天器E的观测角Fig.25 Observation angles of the optical satellite P to the GEO spacecraft E based on ICW equations simulation

5 结论

通过修正非球形摄动偏差和重力加速度二次长期项偏差改进CW方程。将CW方程、ICW方程与真值作仿真对比,ICW方程补偿了非线性偏差的长期项和主要的摄动偏差。在轨迹规划问题上,计算对GEO航天器绕飞的初始相位角区间,成像卫星以该区间内的初始相位角对GEO航天器开始绕飞,可实现在整个绕飞任务中都能以良好的观测角对GEO航天器进行观测。选择合适的初始相位角,分别基于CW方程和ICW方程仿真接近和绕飞的全过程。在仿真中,成像卫星在连续的小推力作用下接近GEO航天器,然后对GEO航天器自然绕飞。基于CW方程的仿真任务失败,而基于ICW方程达到预期目标。在基于ICW方程的仿真中,所需要的总速度增量仅为4.67 m/s,工程上具有很强的可行性。ICW方程可满足精度要求,可用于GEO空间态势感知和在轨服务任务规划。