注意力机制量化剪枝优化方法
何源宏,姜晶菲*,许金伟
(1. 国防科技大学 计算机学院, 湖南 长沙 410073; 2. 国防科技大学 并行与分布计算全国重点实验室, 湖南 长沙 410073)
近年来,基于Transformer的模型(如BERT[1]、GPT-2[2])在机器翻译、句子分类、问题回答等自然语言处理(natural language processing, NLP)任务中实现了最先进的(state-of-the-art, SOTA)成果。在一些具有挑战性的任务上,典型的BERT模型处理效果甚至超过人类[3]。相比传统的循环神经网络[4](recurrent neural network, RNN)模型和长短期记忆[5](long short-term memory, LSTM)模型,基于Transformer的模型采用注意力机制[6],能更有效地捕获输入序列中的上下文信息,使得模型精度显著提高。
在注意力机制的原始计算流程中,注意力机制的输入由查询(Q)、键(K)和值(V)三个激活值矩阵组成。注意力机制首先通过Q和K的相乘计算得到分数矩阵(S),然后采用归一化指数函数(softmax)对分数矩阵进行逐行操作得出概率矩阵(P)。最后将P与V相乘得到输出。相较于RNN和LSTM模型只计算了输入的局部信息,注意力机制计算了每一对查询向量和键向量的注意力结果,从而实现了对全局关系的提取。但由于注意力机制的计算开销和输入序列的长度的平方成正比,全局信息提取带来模型精度提升的同时也使得计算复杂度大幅增加。例如,对于涉及图像或长文本的任务,输入的序列长度可能高达16×103,而对于具有16×103个Token的单个输入序列,BERT-Base中一个自注意力模块的浮点运算次数[7]高达861.9×109。基于注意力机制模型的计算复杂性给实时响应系统和移动设备上的开发部署带来了巨大挑战,模型的轻量化方法是解决计算难题的关键手段。
现有的大部分工作[7-19]着重于对基于注意力机制模型的权重进行量化和剪枝,取得了较好的效果。但是在计算复杂度较高的注意力机制中,大多数模型仍采用单精度浮点表示的稠密激活值矩阵进行运算,激活值不属于权重量化剪枝的范畴,因此计算开销依然很高。本文对基于注意力机制模型的优化训练方法展开研究,通过有效的量化和剪枝方法对激活值矩阵进行量化和剪枝,从而达到大幅降低基于注意力机制模型的计算量和访存量的目的,使得模型推理更适应轻量化智能应用的需求。
1 相关工作
深度神经网络往往被认为是过度参数化的,目前学术界提出了许多方法去除冗余的参数来实现存储或者计算的优化。使用的方法包括量化、剪枝、知识蒸馏、参数共享、专用的FPGA和ASIC加速器等[20-23]。
1.1 深度神经网络的量化方法
量化指用低精度数(如定点8位)表示高精度数(如浮点32位)。除了可以减少神经网络模型占用的空间大小,量化还能在支持低精度运算的硬件中提升模型运算速度。文献[8]利用量化感知训练(quantization-aware training, QAT)和对称线性量化将BERT量化到8位定点整数,同时在下游任务中几乎没有精度损失,从而节省75%的存储空间占用。文献[9]利用权重矩阵的二阶海森信息对BERT进行混合精度和分组量化。文献[10]利用聚类的思想将BERT中99.9%的权重量化到3 bit,剩余权重按照原样存储,但是需要在专用硬件上实现推理过程。为了得到更高的模型压缩比,文献[11]使用三值化的权重分割来获得二值化的权重,文献[12]通过引入二值注意力机制和知识蒸馏[24]得到二值化的权重,虽然二值化后的模型理论上相较于原始模型可以获得32倍的压缩比,但是上述两种方法均会导致模型精度相对于原始模型精度有显著的下降,难以在实际应用中起到较好的效果。
1.2 深度神经网络的剪枝方法
剪枝分为结构化剪枝和非结构化剪枝。非结构化剪枝去除不重要的神经元,可以显著减少模型的参数量和理论计算量,但通用平台擅长的规则计算难以利用其稀疏性,需要专用的硬件或者计算库来支持稀疏矩阵运算。magnitude剪枝[13-15]是应用最广泛也是效果较好的非结构化剪枝方法之一,该方法认为如果一个权重或激活值的绝对值越小,那么对后续结果的影响也越小,则可以将其置为0。文献[14]发现在BERT的预训练过程中,对权重使用magnitude剪枝在低稀疏度(0.3~0.4)情况下不会影响模型在下游任务中的精度,而在高稀疏度(高于0.7)情况下模型难以在下游任务中取得较好的效果。文献[16-17]提出了一种基于训练中权重移动方向的剪枝方法,该方法认为在训练过程中,权重的更新如果越靠近0,则表明该权重越不重要;权重的更新如果越远离0,则表明该权重越重要。
结构化剪枝通常以神经网络中的一个注意力头[18-19]或整层[18]为剪枝的基本单位。结构化剪枝的相关工作输出的模型在计算模式上更匹配CPU、GPU规则计算构架,因此仍然可以通过CPU和GPU完成推理加速,但是存在稀疏度远低于非结构化剪枝的稀疏度等劣势。本文面向实时响应系统和低算力移动设备的计算优化需求,主要研究非结构化剪枝及量化在基于注意力机制模型上的计算优化技术,能够在较好平衡任务准确率的条件下达到良好的计算压缩效果。这种量化剪枝技术能输出更为精简、采用低位宽数据表示的稀疏化模型。面向该类模型,很多工作研究了低位宽智能加速器,通过专用结构高效处理低位宽数据,为低位宽计算和非结构化稀疏计算定制更适合的运算结构,如4位定点运算器、专用稀疏格式的数据运算通路等。相较于CPU、GPU等面向规则计算的体系结构,这些结构能进一步获得大幅能效提升,更加适用于面向实时响应系统和低算力移动设备应用的需求。
2 量化剪枝优化方法
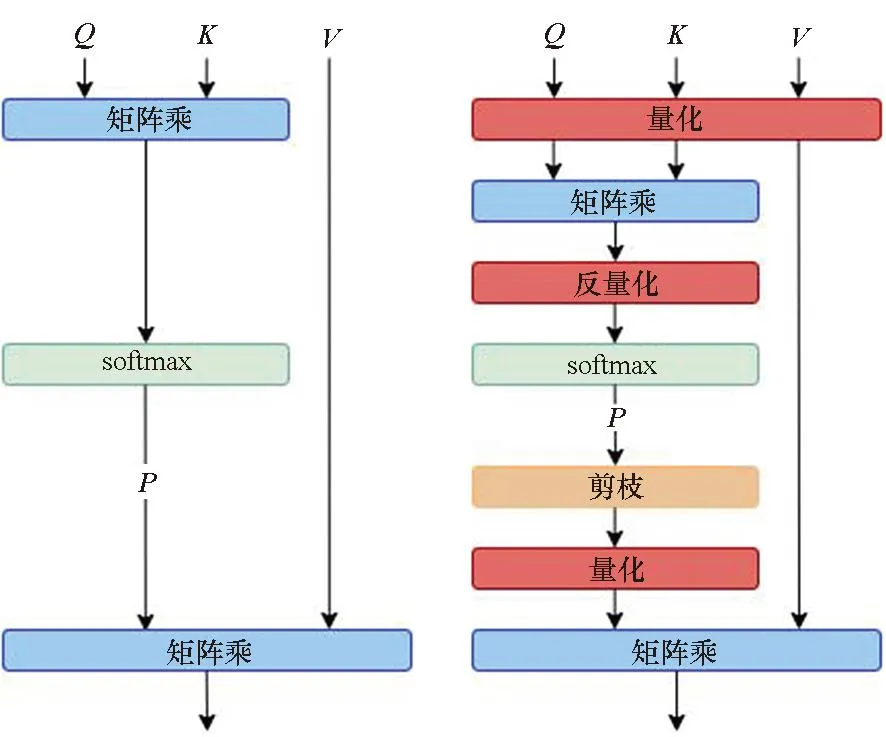
注意力机制的原始计算流程和优化后的计算流程如图1所示,在本文提出的注意力机制模型量化剪枝优化总体流程中,输入激活值矩阵Q、K、V是输入信息在不同空间的表达,在BERT模型中具有相同的维度:①对于给定的输入激活值矩阵Q、K、V,首先量化Q和K到4位或8位定点整数,计算分数矩阵的结果;②将分数矩阵进行反量化并送入softmax得到P;③将P中绝对值低于阈值的数剪枝为0;④将稀疏的P量化到4位或者8位定点整数并将其与量化后的V相乘,得到注意力机制的输出结果。第②步和第③步进行反量化和量化操作的原因是直接将线性量化的数据送入softmax,这一类非线性运算会显著影响模型在数据集上的精度[25],同时为了后续量化计算,需要将剪枝后的结果进行量化。考虑到对计算过程进行简化,该方法根据是否为同一矩阵乘的输入采取了分组量化,即Q和K为一组,P和V一组。同一组的两个矩阵量化到相同的比特数,而不同组之间可以量化到不同比特数。
2.1 激活值矩阵的对称线性量化方法
对称线性量化、非对称线性量化、非线性量化、K-means量化等是典型的模型量化方法[21]。对称线性量化相较于其他方法所需的硬件计算更加简单,更易于高效的专用加速器实现。本文采取的激活值矩阵的kbit对称线性量化公式定义如下:
(1)
其中:Q是量化函数;r是输入的原始数据;S是量化缩放因子;α是量化到kbit时的最大值,例如,当量化到4位时,α=7。由于注意力机制的输入是动态变化的,故使用指数滑动平均(exponential moving average, EMA)来收集其信息,并在训练的过程中确定S。clip是截断函数,确保量化后的值不超出kbit所能表示的范围。round函数起到四舍五入的作用。对称线性量化本质上是将输入r映射到对称区间[-α,α]之中。对于反量化公式定义如下:
DQ(S,q)=S×q
(2)
式中,DQ是反量化函数,q表示输入的量化值。量化过程和反量化过程均采用相同的S。训练过程中为了传递量化误差,本文采用量化感知训练实现伪量化;同时考虑到round函数的不可导性,采用直通估计器(straight-through estimator, STE)进行梯度反向传播。
2.2 渐进剪枝训练
渐进剪枝策略[26]能有效避免剪枝带来的模型精度显著下降,参考其原理,本文采用magnitude剪枝方法实现,在每次剪枝迭代时,将待剪枝的激活值矩阵中绝对值低于预设阈值的数剪枝为0。训练过程采用三段式渐进剪枝方法,在总迭代次数为T的训练过程中,前ti次迭代只进行模型的微调;在ti到tf次迭代的过程中稀疏度s从0提升到预设的目标稀疏度st,在这期间s以三次函数的趋势呈先快后慢的非线性增长;最后维持目标稀疏度st进行微调实现精度的回调。其中稀疏度s表示一个矩阵中数值为0的权重所占的比值,具体取值如分段函数(3)所示:
(3)
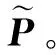
3 实验分析
3.1 实验设置
本文在BERT-Base[1]模型上针对通用语言理解评估[27](general language understanding evaluation, GLUE)基准进行了一系列的实验分析。GLUE包含了9个数据集来对自然语言模型进行训练、评估和分析,分别为CoLA、RTE、MRPC、STS-B、SST-2、QNLI、QQP、MNLI、WNLI,但是本文没有在WNLI数据集上进行评估,因为它通常被认为存在一定的问题[1]。此外,本文也在问答任务SQuAD v1.1[28]上进行了评估。对于MRPC、QQP、SQuAD v1.1数据集采用F1值评估;对于STS-B数据集用皮尔逊相关系数评估;对于CoLA数据集用马修斯相关系数评估;对于GLUE中剩余的数据集均采用准确率评估。所有数据集的评估指标都与模型的精度成正相关。
实验中BERT实现代码是基于HuggingFace 的Transformer库[29],并在PyTorch深度学习框架完成了量化剪枝实验和模型精度的评估。所有的实验均运行在单GPU(NVIDIA Tesla V100 PCIe 32 GB)上。因为本文提出的方法不涉及预训练,故直接将预训练好的BERT-Base模型在数据集上进行量化剪枝训练。CoLA、RTE、MRPC、STS-B数据集训练时的批大小为8,学习率为2×10-5;SST-2、QNLI、QQP、MNLI、SQuAD v1.1数据集训练时的批大小为32,学习率为3×10-5。每次训练为10个epoch:①前3个epoch对应渐进稀疏的第一阶段,模型的稀疏度为0;②接下来4个epoch对应渐进剪枝的第二个阶段,此时稀疏度s随时间从0增长到目标稀疏度st;③最后3个epoch对应渐进剪枝的第三个阶段,此时维持目标稀疏度st对模型进行微调完成最后的训练,该阶段可以在一定程度上缓解剪枝带来的模型精度损失。在整个训练过程中,都实施本文提出的对称线性量化流程。
3.2 实验结果
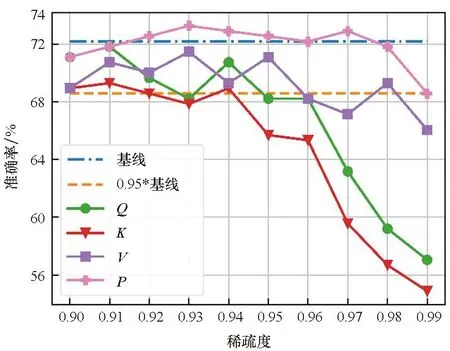
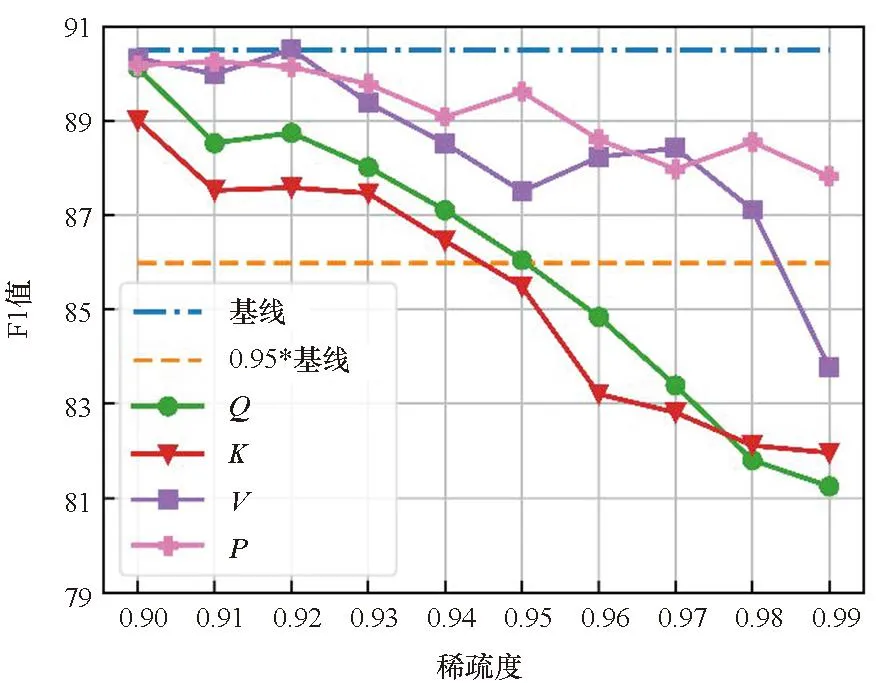
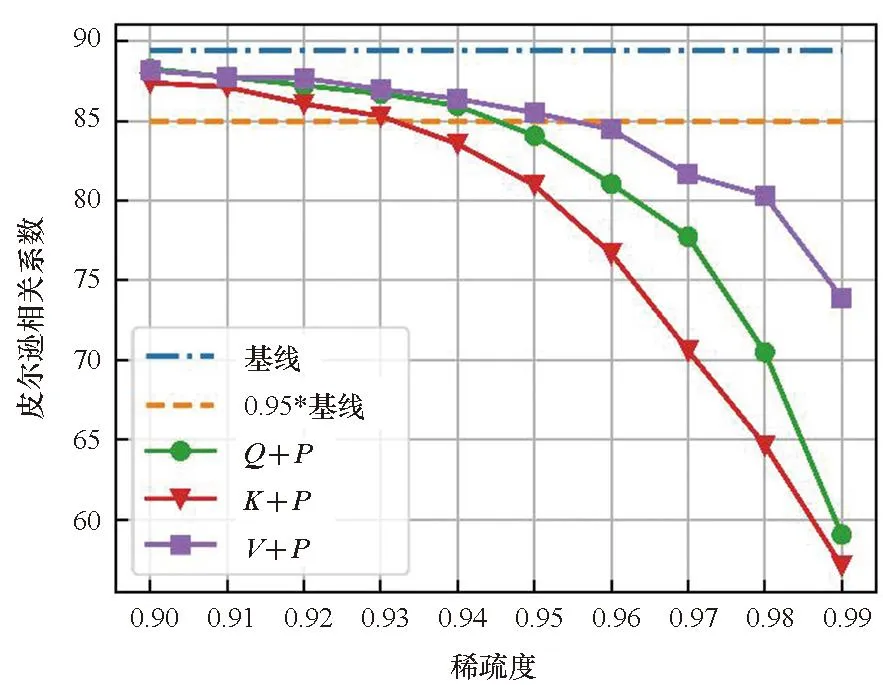
图2表明了各数据集在不同的目标稀疏度st(大于0.9)下对Q、K、V、P单独剪枝的结果,基线表示没有进行剪枝和量化的结果, 0.95*基线表示基线的95%的精度。首先,结果显示Q和K在剪枝效果上具有一致性:即Q和K的结果曲线具有相似的变化趋势。而P和V也有类似的性质。这表明同一个矩阵乘的两个输入具有相似的剪枝效果。其次,随着稀疏度的提升,除CoLA数据集外,P和V的剪枝效果逐渐优于Q和K。本文认为这是因为P之前的softmax运算隐式的将重要的信息进行了提取,并赋予其较大的值,这也表明P更适合进行剪枝。最后,在较高的稀疏度(大于0.95)下,所有矩阵剪枝后的模型精度均出现了明显的下降,尤其是Q和K。
(b) RTE数据集(b) RTE dataset
(c) MRPC数据集(c) MRPC dataset
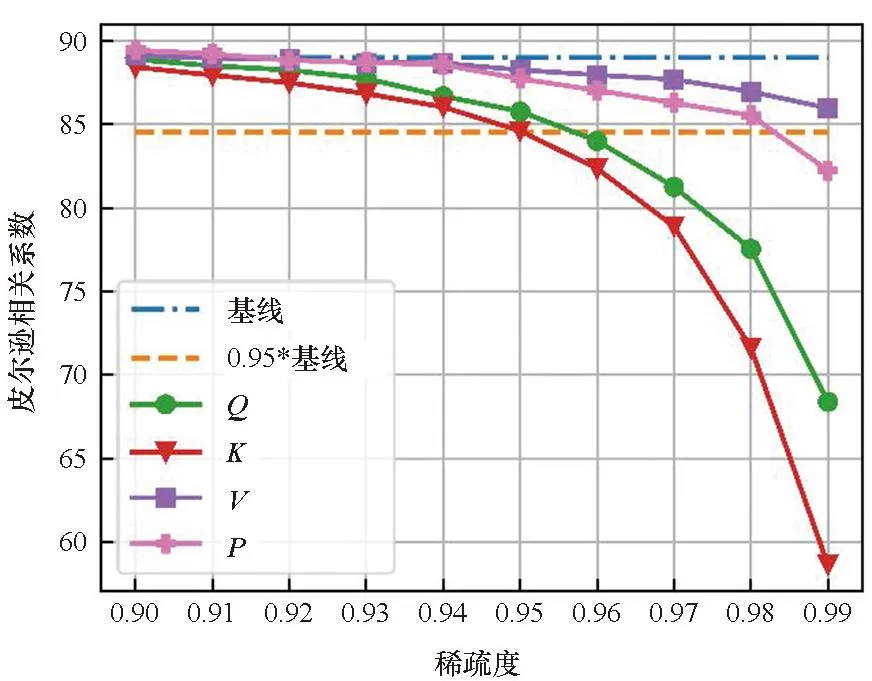
(d) STS-B数据集(d) STS-B dataset
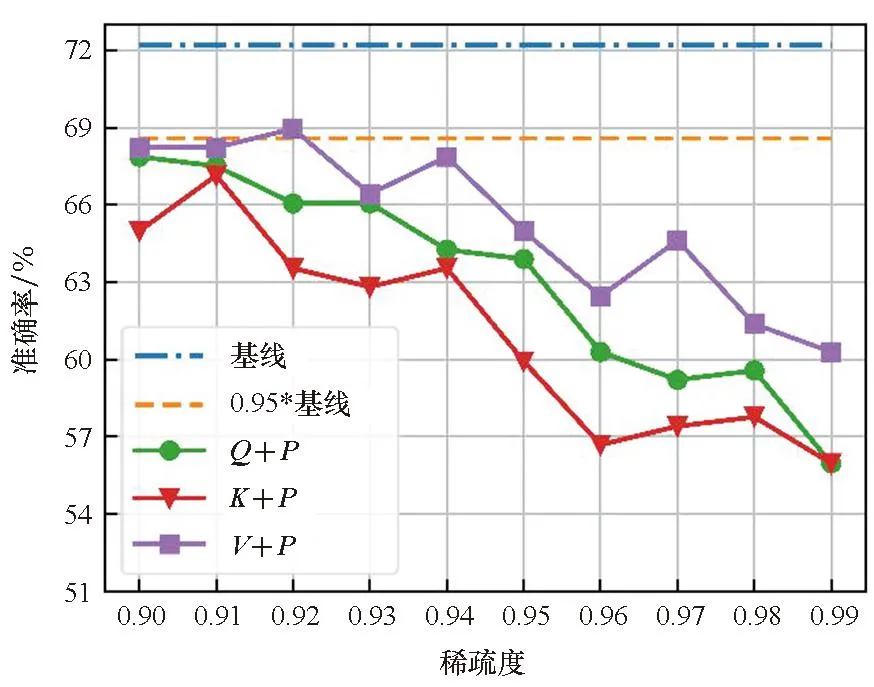
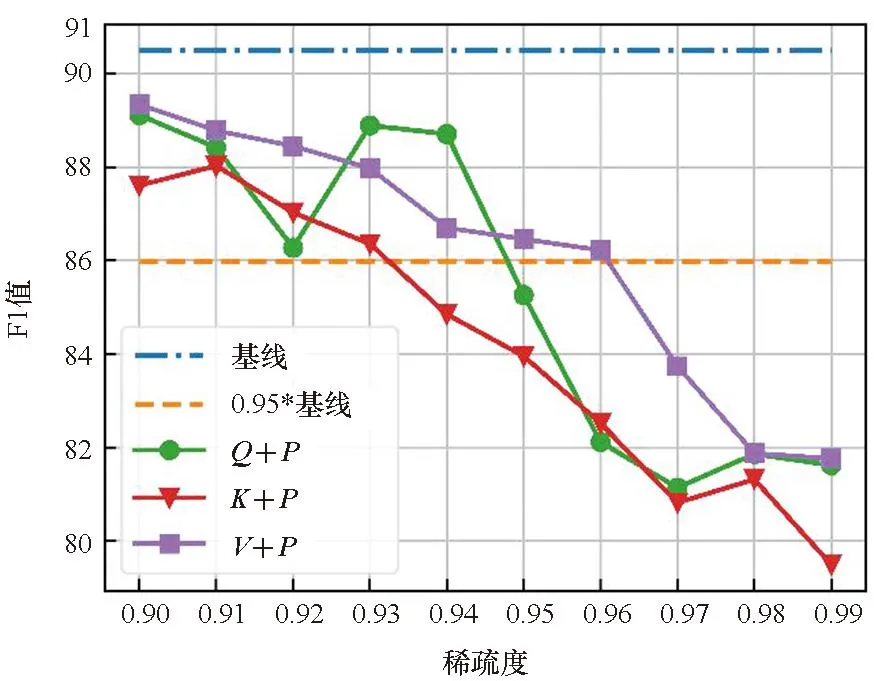
在单独剪枝的基础上,本文还比较了Q、K、V分别和P进行联合剪枝后模型精度的差异,如图3所示。从图2和图3的对比可以看出,在大多数情况下,Q、K、V在单独剪枝中具有最好效果的那一个矩阵,在和P进行联合剪枝时也会具有最好的效果。但是Q、K、V分别和P的联合剪枝比单独剪枝时的精度下降得更快。同时考虑到P的大小与输入序列长度的大小的二次方成正比,故本文在接下来的量化实验中只针对P进行剪枝。
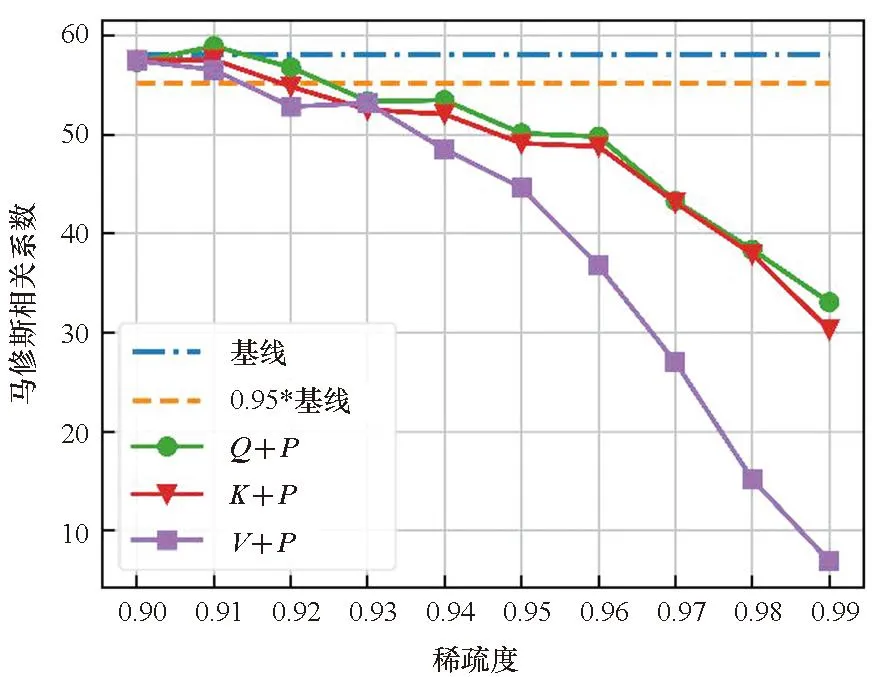
(a) CoLA数据集(a) CoLA dataset
(b) RTE数据集(b) RTE dataset
(c) MRPC数据集(c) MRPC dataset
(d) STS-B数据集(d) STS-B dataset
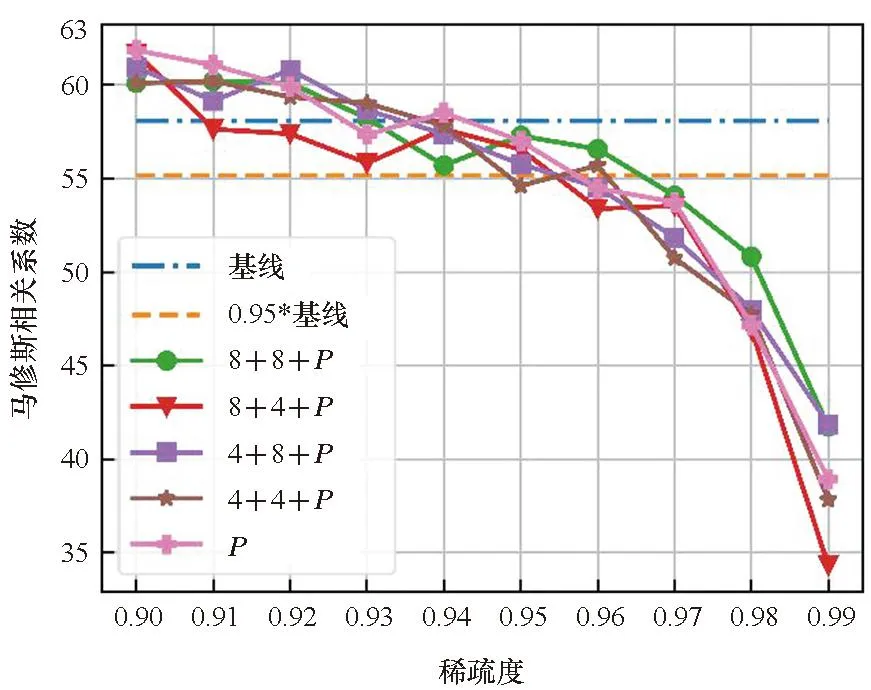
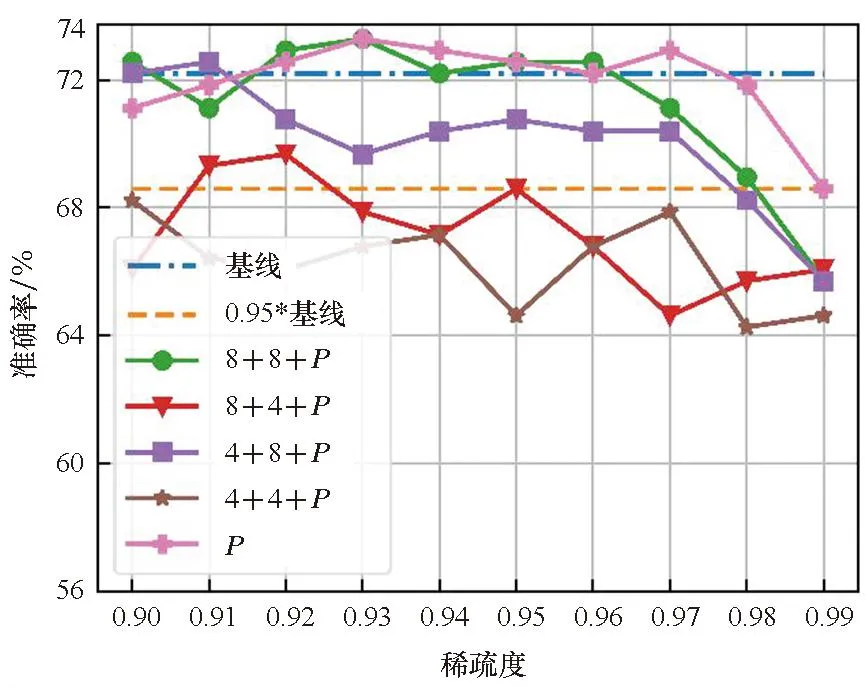
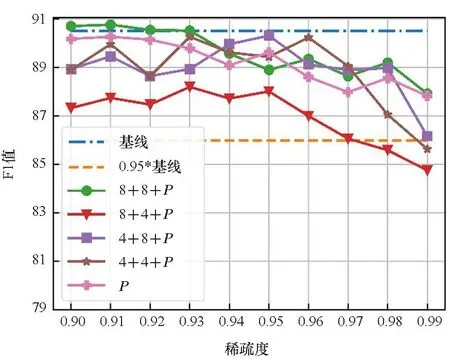
实验结合了量化和剪枝来探究量化带来的影响。实验设置了两种量化位宽,分别是4位和8位。结合两种量化位宽的设定和分组量化,图4展示了四种量化方案和剪枝共同优化的结果。图例中的8+4表明对于Q和K量化到8位,P和V量化到4位。从图4中可以清楚地看到,在大多数情况下,量化对P的剪枝效果的影响较小。在STS-B数据集中,即使量化比特方案为4+4,在相同稀疏度水平下,量化剪枝比非量化剪枝还能获得更好的结果,这表明量化和剪枝在实际的应用中具有正交性,同时量化能提升模型的鲁棒性。
在STS-B和CoLA数据集中,不同量化比特方案产生的模型精度差异较小。但是在RTE和MRPC数据集中,不同的量化比特设定带来了明显的精度差异,表明不同的数据集对于量化的敏感程度不一样。同时较低的量化比特设定并不意味着较低的模型精度。例如,4+4的量化方案在CoLA、MRPC、STS-B数据集中并不是精度最低的,甚至在STS-B数据集中,4+4的量化方案能获得最好的整体效果,而8+8的量化方案在整体效果表现上最差。
(a) CoLA数据集(a) CoLA dataset
(b) RTE数据集(b) RTE dataset
(c) MRPC数据集(c) MRPC dataset

(d) STS-B数据集(d) STS-B dataset
在图2到图4的三组实验中,RTE数据集均为结果波动较大的数据集之一,本文认为是RTE数据集对于量化和剪枝较敏感,特别是在量化和剪枝协同优化时,波动更为明显。总体来说,即使在较高的稀疏度下,本文的量化方案也不会使模型的精度产生显著的下降。
3.3 和Sanger的比较

一些相关研究表明[8-10],针对深度神经网络一定程度的压缩(量化、剪枝、知识蒸馏等)能够提升模型的鲁棒性,因此使得压缩后模型的精度略微超过基线模型,而当压缩率继续提升时模型的精度可能会逐渐下降。但目前尚无相关研究能够定量说明什么程度的压缩能起到泛化的作用。从定性的角度,本文分析深度学习模型一般具有较大的信息冗余和噪声,一定的压缩使得这些冗余噪声被更高比例去除,因此使得模型精度得以保持甚至略有上升。
3.4 计算轻量化分析
模型稀疏量化可以从计算次数和数据表示两方面降低模型推理的计算量,提升计算速度。以BERT模型的一个自注意力头模块为例,推理任务的绝大多数计算是Q、K、P、V涉及的矩阵运算,对于两个n阶方阵的矩阵乘法,其他配套操作(包括量化、反量化、softmax、剪枝)的计算量约为其1/n,当n较大时,这部分运算量可忽略。模型计算复杂度一般由矩阵乘加量代表。当把模型稀疏度提升至x%时,稀疏模型计算复杂性约可降为原模型稠密矩阵计算的1-x%。稀疏矩阵一般以CSR稀疏格式存储,大小约为稠密矩阵的2(1-x%)。同时,当模型将原有数据位宽W量化为W/y时,压缩后数据的存储量将降低为原来的1/y。
根据上述分析以及表1所获得的BERT模型稀疏量化结果,在P×V计算稀疏度为95%、所有矩阵4+4量化协同优化下,得到式(4):
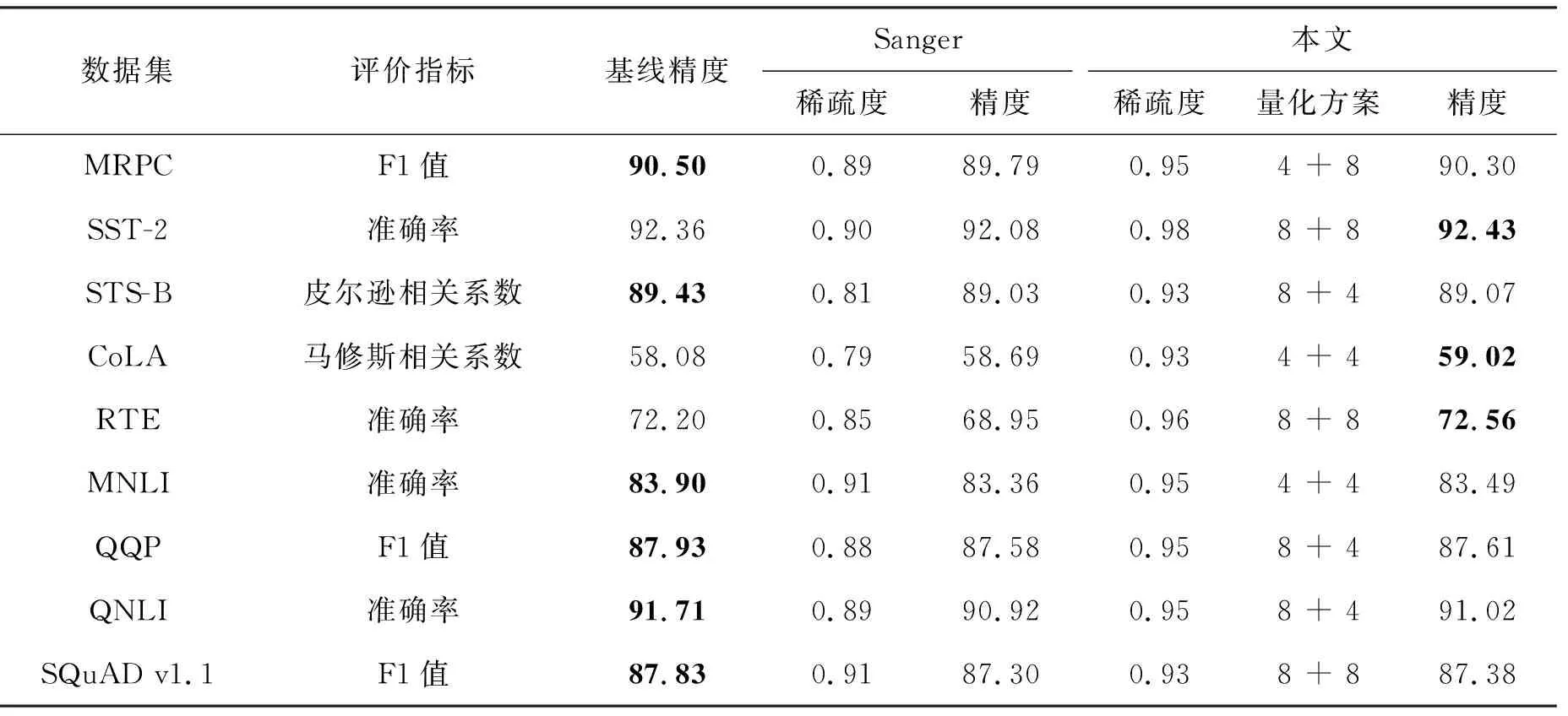
表1 不同数据集上的量化剪枝结果

(4)
整个模块的理论推理速度可提升约16倍。其中:a为P×V计算量占比,(1-a)为Q×K计算量占比,在该模块中a约为50%;sP为P的稀疏度;NPV和NQK分别为P、V和Q、K量化到N比特后N位定点运算相较于32位浮点运算的加速比,根据硬件运算单元速度的一般结论,4位定点乘加单元的运算速度为32位浮点乘加单元运算速度的8倍以上。就存储量而言,4+4量化后Q、K、V占用存储空间的大小可降为原始的1/8,同时在95%稀疏度下P的大小约为原始的1/80。
上述分析面向可有效处理稀疏运算和低位宽量化运算的定制加速器,有较多前沿相关工作[3,7]基于此思路开展,相较于通用平台,加速器不仅能高效处理上述运算,还可消除CPU、GPU等由于指令和调度执行带来的额外控制开销,大幅提升最终性能。
4 结论
针对基于注意力机制模型计算复杂度和访存开销过高等问题,本文提出了一种量化剪枝协同优化方法,该方法通过采用对称线性量化和渐进剪枝来降低注意力机制的计算复杂量。本文提出的方法在较低或者没有精度损失的情况下,在BERT模型上有着较好的实验效果,对于GLUE基准和SQuAD v1.1数据集,该方法将注意力机制运算涉及的Q、K、V、P采用分组量化,其中Q和K为一组,V和P为一组,分别量化到4位或者8位,并且剪枝P,最终可以得到0.93~0.98的稀疏度,大幅度降低模型计算量。在SST-2、CoLA、RTE数据集上,该优化方法得到的模型在精度上甚至超过了基线。
本文提出的方法在各方面也优于Sanger稀疏模式,包括稀疏度和最终的模型精度。但本文所提出优化方法是非结构化稀疏模式,该稀疏模式具有稀疏度高和难以在通用平台加速等特点,故下一步的工作展望为在专用的硬件平台上充分利用其量化和稀疏特性,将量化剪枝的理论计算性能提升转换为实际推理能耗和延迟的降低。

