漂浮式光伏电站中漂浮方阵的流荷载数值预报研究
黄国珍 席凯 冯榆坤 陈熹 陈长馥 陈作钢
摘 要:漂浮式光伏电站遭遇突发泄洪等极端情况时流荷载骤增,对漂浮方阵的整体安全构成威胁,正确评估漂浮方阵的流荷载变得十分重要。以国家能源菏泽发电有限公司建设的某大型漂浮式光伏电站为例,首先基于计算流体力学(CFD)方法对单个浮体模型所受流荷载进行数值研究,确定符合计算要求的最优网格数量;然后通过计算光伏组件以10行10列(即10×10)方式排布的漂浮方阵在0°~90°流向角下的流荷载,得到该漂浮方阵最大流荷载流向和初步的流荷载分布规律;最后通过对比分别利用3D、2.5D和2D计算方法得到的30×28漂浮方阵流荷载计算结果,完成了195×98漂浮方阵整体流荷载的预测。研究结果显示:1)不同流向角下,0°流向角时漂浮方阵所受的流荷载最大,随着流向角增大流荷载逐渐减小;当流向角为90°时,流荷载达到最小值,仅为0°流向角时的48%左右。2) 0°流向角时,迎流第1行浮体所受流荷载最大,受遮蔽效应影响,后续各行的流荷载逐渐减小。3)漂浮方阵所受流荷载基本不随列变化;30×28漂浮方阵中间某列采用2D和2.5D计算方法得到的漂浮方阵流荷载与采用3D计算方法所得的结果一致。研究成果可为漂浮式光伏电站等类似大规模漂浮式结构物的流荷载预报提供参考。
关键词:漂浮式光伏电站;漂浮方阵;流荷载;数值模拟;2.5D计算方法
中图分类号:TM615/TU318+.1 文献标志码:A
0 引言
太阳能是一种储量巨大的清洁能源,具有安全可靠、分布范围广、无污染、可以持续利用的特点[1],光伏发电是其主要利用方式之一。近年来,中国光伏产业发展迅速,截至2022年9月底,中国累计光伏发电装机容量达3.58亿kW,连续8年稳居世界首位,但日益减少的土地资源限制了该产业的进一步发展[2]。相较于传统的陆上光伏电站,水上光伏电站可布置在水库、鱼塘、湖泊及采煤塌陷积水区等水面上,具有运营成本低、发电效率高、不占用土地资源等优势,已然成为未来光伏产业的新增长点[3]。中国的海岸线长达3.2万km,海域面积近300万km2,且大部分水域都具备布置水上光伏电站的自然条件;而且中国湖泊众多,全国湖泊总面积约为9.1万km2,面积在1000 m2以上的湖泊超过2700个;此外,中国还拥有大量的水库、鱼塘和难以开发利用的采煤塌陷区,这些区域具有发展水上光伏电站的天然优势[4]。
根据水上光伏电站的布置特点,可以将其分为固定式水上光伏电站和漂浮式光伏电站两种,受限于建设成本和作业难度,前者一般布置在浅水区域,而后者不受水深限制,具有更加广阔的发展前景[5]。
漂浮式光伏电站浮于水面,需要由系泊系统限制其移动范围[6],因此在此类光伏电站建设之前,必须对其所受的环境荷载进行计算分析,以保证光伏电站的整体安全[7]。一般情况下,流荷载在漂浮式光伏电站的整体环境荷载中属于次要成分,但遭遇突发泄洪等紧急情况时,流荷载会急剧增大[8],成为影响此类光伏电站整体安全的重要因素;在漂浮式光伏电站由内陆湖泊走向近海的过程中,流荷载的影响也是不可忽略的;同时,由于流体介质不同,流荷载可能会体现出与风荷载不同的特点。综上所述,需要对此类光伏电站所受的流荷载进行深入研究,以保证其安全性[9]。
已有学者针对漂浮式结构物所受流荷载进行了相关研究。孔耀华等[10]计算了170 m×170 m漂浮方阵在不同来流方向时的流荷载分布,结果显示:迎流向的上游浮体对下游浮体有显著的遮蔽效应;在迎流向第20行浮体之后浮体的流荷载基本趋于稳定。Buljac等[11]通过水池试验研究了处于漂浮状态的单个海上风力涡轮机在风荷载、流荷载和波浪荷载共同作用下的整体受力。Choi等[12]模拟了水流从前面、后面、侧面3个方向接近漂浮式光伏电站时,漂浮单元所受的阻力,并计算了1个以3行5列(即3×5,下文均采用m×n的表示方式,代表该光伏方阵的规模为m行n列)排布的漂浮光伏阵列在风、浪、流共同作用时的结构安全性。
鉴于流荷载与风荷载的相关研究在研究思路和计算方法上存在相似之处,因此,漂浮式结构物流荷载的研究与计算可以借鉴风荷载的相关研究成果。针对结构物风荷载,王禹衡等[13]研究了A类剖面在风荷载作用下,海洋平台上各结构物之间的遮蔽效应与物体间距、物体尺寸及非满实结构等因素之间的关系,研究发现:物体纵向间距越大,遮蔽效应越弱;并且干扰物的遮蔽作用与其满实率正相关,满实率越大,遮蔽效应越明显。黄张裕等[14]研究了光伏组件以5×1方式排布的光伏阵列在不同安装倾角、不同风向角下的风荷载取值,并提出了光伏阵列分区设计的思路。
目前,国内外学者对于漂浮式结构物所受流荷载的研究大多着眼于单体或小型阵列,对于包含数万个单元的大型方阵,尚无成熟的可准确预报其流荷载分布的方法。鉴于大型漂浮方阵迎流面的上游光伏组件对下游光伏组件、边缘光伏组件对方阵内部光伏组件均存在明显的遮蔽效应,其流荷载分布规律与小型漂浮阵列的差异较大,现有单体或小型漂浮阵列的荷载分布规律很难应用在大型漂浮方阵的流荷载计算中。此外,由于网格数量的限制,通过建立完整漂浮方阵3D流体模型(3D计算方法)求解其整体流荷载的方法在工程实践中很难实现。为解决上述问题,本文以国家能源菏泽发电有限公司建设的某大型漂浮式光伏电站为例,首先基于计算流体力学(CFD)方法[15]对单个浮体模型进行网格无关性验证,以确定符合计算要求的最优单元网格数量;然后通过计算光伏组件以10×10方式排布的漂浮方阵在0°~90°流向角下的流荷载分布,得到漂浮方阵最大流荷载流向和初步的流荷载分布规律;最后通过对比分析30×28漂浮方阵的3D、2.5D和2D流荷载计算结果,完成195×98漂浮方阵整体流荷载的预测。需要说明的是,不同于3D和2D计算方法,2.5D流荷载计算方法是笔者所在课题组提出的一種特殊计算方法,其可以极大减小计算量。以期本研究可为类似于漂浮式光伏电站漂浮方阵的大型漂浮式结构物的流荷载预测提供方法。
1 单个浮体的流荷载计算
在对实体漂浮方阵整体流荷载进行计算之前,先基于CFD方法对单个浮体模型进行网格无关性验证,以确定符合计算要求的最优单元网格数量,控制计算成本。通常情况下,数值计算的效率和准确性很大程度上取决于模型的网格密度,网格密度越大,计算精度越高,但网格密度过高会极大增加计算成本,不符合工程实践的要求。本文首先根据计算经验确定基本网格密度,然后在此基础上进行增减,若计算结果随网格密度的变化较小,则认为该范围内的网格密度可信,即计算结果与网格密度无关。
1.1 计算设置
单个浮体的模型如图1所示,该浮体由3个相连的模块组成,自左向右各模块的尺寸分别为450 mm×300 mm、1280 mm×450 mm、450 mm×430 mm,吃水深度为50 mm。图中:坐标原点位于模型中心;xy平面位于静水面;x轴指向正北;y轴指向正东;z轴按右手法则铅直向上。
单个浮体模型的计算域示意图如图2所示,不同流向的建模和计算通过旋转模型实现;流域入口设置为速度入口,出口为压力出口;顶部水面为对称面,底部边界及模型表面均为无滑移壁面,其余壁面为滑移壁面;水的计算流速为1 m/s。求解器采用基于CFD方法的通用软件STAR-CCM+,湍流模型选择realizable k-ε模型[16],近壁面流动采用标准壁面函数模拟,速度压力耦合采用SIMPLE算法[17],空间离散采用标准格式,其余离散项均采用二阶迎风格式。
1.2 网格独立性验证
相关研究发现,浮体所受流荷载与其迎流面积呈正相关[10]。因此,此处只针对迎流面积最大的北向来流进行单个浮体模型的网格独立性验证,并将计算得到的单个浮体模型水平流荷载利用式(1)换算为无量纲的流荷载系数Cf进行对比。
式中:F为单个浮体模型所受流荷载,N;ρ为流体密度,kg/m3;A為单个浮体模型的特征面积,m2;v为液体的计算流速,m/s。
单个浮体模型的网格独立性验证结果如表1所示。表中的相对偏差以单元网格数量为263万个时得到的流荷载系数为基础进行计算。
由表1可知:北向来流条件下,单元网格数量从263万个减少至114万个时,单个浮体模型的流荷载系数的相对偏差均在3%以内;但当单元网格数量减少至83万个时,单个浮体模型的流荷载系数的相对偏差达到了11%以上,误差较大,说明不宜用于实体漂浮方阵的计算。因此,本文选择114万个单元网格数量的划分方案进行后续实体漂浮方阵的流荷载计算。
2 最大流荷载流向的确定
若要确定最大流荷载的流向,需先分析流荷载的分布规律。为便于描述流荷载分布规律,本文规定漂浮方阵东西方向为“行”,由北向南计数;南北方向为“列”,由西向东计数。
鉴于目前漂浮方阵的结构形式复杂、规模日趋庞大,通过模拟完整漂浮方阵3D流场来求解流荷载的传统CFD方法已很难应对目前大型漂浮方阵的流荷载计算问题。为提高计算效率、节约计算成本,本文提出了一套新型的大型漂浮方阵流荷载数值预报方法:首先对小型10×10漂浮方阵的流荷载进行计算,得到其最大流荷载的流向及初步的流荷载分布规律;然后对比分析分别通过3D、2.5D、2D计算方法得到的30×28漂浮方阵流荷载计算结果,得到流荷载分布规律,从而实现对195×98漂浮方阵整体流荷载的预测。其中,2.5D计算方法是指仅计算南北向1列浮体、东西两侧采用周期性边界条件的计算方法。
为确定最大流荷载的流向,本文对10×10漂浮方阵在0°、10°、20°、30°、45°、60°、75°、90°共8个流向角下的流荷载进行计算,该漂浮方阵的计算域示意图如图3所示。其中,0°流向角对应北向流,90°对应西向流;考虑到模型的对称性,90°之后的流向不再进行计算;流域顶部边界为对称面,底部边界为无滑移壁面,四周边界根据流向的变化,迎流面为速度入口,其余边界为压力出口。
由图4可知:0°流向角下,漂浮方阵的流荷载系数最大,说明该流向角下漂浮方阵所受的流荷载最大;随着流向角的增大,漂浮方阵迎流面积逐渐减小,流荷载系数也随之减小,其整体流荷载也相应减小;流荷载系数在90°流向角时达到最小值,约为0°流向角下的48%,这也意味着此时漂浮方阵的整体流荷载约为0°流向角下时的48%,即北向来流为漂浮方阵最大流荷载的流向。因此,本文后续重点研究北向来流时漂浮方阵的流荷载分布,其他流向暂不考虑。
3 漂浮方阵模型流荷载的3D、2.5D和2D计算方法结果分析
本文计算漂浮方阵模型流荷载时,模型采用的尺寸为实际漂浮方阵的尺寸。
3.1 流荷载的3D计算结果
为得到最大流荷载流向时流荷载沿漂浮方阵行和列的变化规律,本节对北向来流条件下30×28漂浮方阵的整体流荷载进行计算。30×28漂浮方阵的计算域示意图如图5所示,计算域入口距漂浮方阵北部边缘100 m,出口距漂浮方阵南部边缘300 m;流域宽度为150 m,高度为50 m,数值模拟方法与前述单个浮体模型时的相同。考虑到流场的对称性,将计算域最东侧边界设为对称面,因此,30×28漂浮方阵等效为30×56漂浮方阵。
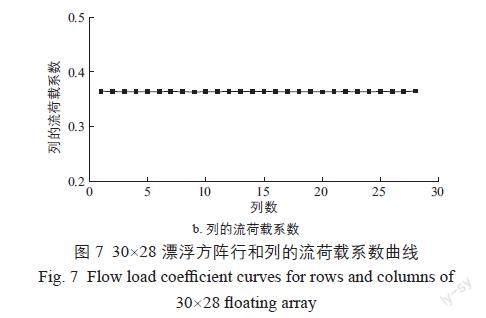
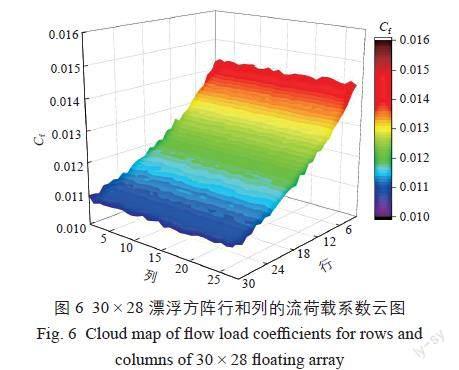
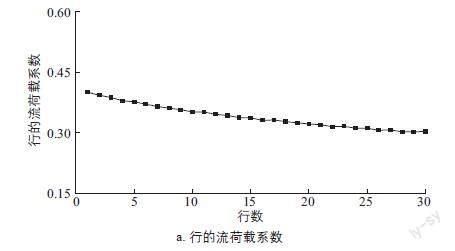
计算得到北向来流条件下30×28漂浮方阵的整体流荷载后,提取各浮体所受的流荷载,绘制该漂浮方阵行和列的流荷载系数云图和曲线图,分别如图6、图7所示。其中,图7中漂浮方阵行(或列)的流荷载系数由每行(或列)的单个浮体的流荷载系数求和得到。
由图6、图7可知:漂浮方阵所受流荷载在北侧迎流第1行有最大值,受上游浮体遮蔽效应的影响,由北向南流荷载逐渐减小,直到最后一行;此外,由于浮体模型东西方向上的形状相似,且各列间距较小,因此漂浮方阵所受流荷载基本不随列的变化而变化。
3.2 流荷载的3D、2.5D和2D计算结果对比
结合上文利用3D计算方法得到的漂浮方阵流荷载结果可以发现:北向来流条件下,漂浮方阵整体流荷载沿列均匀分布,即漂浮方阵外围与漂浮方阵内部浮体单元所受流荷载的大小及分布规律基本相同,因此,只需计算漂浮方阵中间1列的流荷载即可得到完整漂浮方阵的流荷载分布。同时,由于各列浮体的东西向间距仅为133 mm,与单个浮体的东西向长度相比属于小量,对于漂浮方阵受力的影响较小,在进行漂浮方阵流荷载计算时可以将各列浮体的东西向间距忽略。因此,本节分别采用2.5D和2D两种计算方法对30×1实体漂浮方阵的流荷载进行简化计算,并为验证这两种计算方法得到的流荷载计算结果的可靠性,将二者的计算结果与采用3D计算方法得到的30×28漂浮方阵中第28列处的流荷载系数计算结果进行了对比,具体如图8所示。需要说明的是,分别采用3D、2.5D和2D计算方法时,模型的网格密度、计算设置、计算域高度及长度均保持一致;2.5D计算方法的计算域与图5中的设置一致。
由图8可知:采用2D、2.5D和3D 3种计算方法得到的浮体流荷载系数(即浮体流荷载)沿行的分布规律基本相同,并且3种计算方法得
到的总流荷载系数(即总流荷载)的相对偏差均在1%以内。因此,后续可以采用2D计算方法进行北向来流时漂浮方阵整体流荷载的预测。
4 流荷载与流速的关系
基于2D计算方法对北向来流时某列(共30行)浮体在流速分别为0.183、0.500、1.000、1.500及2.000 m/s时的流荷载系数进行计算,计算结果如图9所示。
由图9可知:各流速下该列浮体的流荷载系数沿行的分布规律相似,最大值均出现在迎流第1行,随着行数的增加流荷载系数逐渐减小;当流速由0.183 m/s扩大至2.000 m/s时,总流荷载系数由0.37变为0.34,变化幅度很小;同时,随着流速的增大,流荷载系数的变化幅度也在逐渐减小。因此,可认为无量纲的流荷载系数与流速无关,不同流速下漂浮方阵的流荷载系数仍可用前述的流速为1 m/s时的结果进行估算。
5 195×98漂浮方阵的流荷载预测
根据上文分别利用3D、2.5D和2D计算方法得到的实体漂浮方阵的流荷载系数计算结果可以发现,北向来流条件下,漂浮方阵整体流荷载基本不随列变化。因此,195×98漂浮方阵整体流荷载可通过2D计算方法预测得到,預测结果如图10所示。
由图10可知:流荷载系数在迎流第1行为最大值,且由北向南逐渐减小,这与前文得到的结论一致。
6 结论
本文以国家能源菏泽发电有限公司建设的某大型漂浮式光伏电站为例,通过对比分析30×28漂浮方阵分别采用3D、2.5D和2D计算方法时得到的流荷载计算结果,完成了195×98漂浮方阵整体流荷载的预测,得到以下结论:
1)不同流向角下,0°流向角时漂浮方阵所受的流荷载最大,随着流向角增大流荷载逐渐减小;当流向角为90°时,流荷载达到最小值,仅为0°流向角时的48%左右。
2) 0°流向角时,迎流第1行浮体所受流荷载最大,受遮蔽效应影响,后续各行的流荷载逐渐减小。
3)漂浮方阵所受流荷载基本不随列变化;30×28漂浮方阵中间某列采用2D和2.5D方法计算得到的漂浮方阵流荷载与采用3D计算方法所得的结果一致;因此,针对列间距较小且模型展向形状变化不大的阵列,可以采用2D计算方法实现大规模浮式阵列整体流荷载的低成本预测。
4)无量纲的流荷载系数不随流速的增大而增大,基本保持不变,说明其与流速无关。
致谢:本研究得到上海超级计算中心的大力支持,在此深表感谢。
[参考文献]
[1] 马维唯.国际太阳能发电产业现状及发展趋势[J].太阳能,2020(1):5-12.
[2] 赵然,邵蒋宁,诸荣耀,等.水面漂浮式光伏电站的经济性分析[J].太阳能,2023(1):22-29.
[3] 吴继亮, 梁甜, 糜文杰, 等.水上漂浮式光伏电站的发展及应用前景分析[J]. 太阳能,2019(12):20-23.
[4] 陈东坡.我国水上光伏电站的新机遇、新发展和新挑战[J].电子产品世界,2017,24(5):3-5.
[5] 石涛.水上光伏电站站址选择及总平面布置设计要点探讨[J].太阳能,2021(6):50-57.
[6] 孔耀华,王磊,陈作钢,等.漂浮式光伏电站漂浮方阵的锚泊计算研究[J].可再生能源,2019,37(10):1434-1439.
[7] 肖福勤,陈作钢,代燚,等.漂浮式光伏电站方阵环境载荷计算方法研究[J].工程力学,2020,37(3):245-256.
[8] 宋肖锋,陈作钢,肖福勤,等.漂浮式光伏电站方阵风载荷数值研究[J].太阳能学报,2020,41(10):136-143.
[9] 吴慕丹,袁万.漂浮式水上光伏电站对湖库风生流作用机理的研究[J].太阳能,2021(12):30-36.
[10] 孔耀华,肖福勤,陈作钢,等. 漂浮式光伏电站漂浮方阵流载荷数值计算研究[J]. 水动力学研究与进展(A辑),2019,34(2):218-223.
[11] BULJAC A,KOZMAR H,YANG W X,et al. Concurrent wind, wave and current loads on a monopile-supported offshore wind turbine[J]. Engineering structures, 2022, 255:113950.
[12] CHOI Y K, LEE J H. Structural safety assessment of ocean-floating photovoltaic structure model[J]. Israel journal of chemistry, 2015, 55(10):1081-1090.
[13] 王禹衡,汪敏.考虑遮蔽效应的海洋平台风载荷计算研究[J].船舶工程,2018,40(S1):298-302.
[14] 黄张裕,阎虹旭.太阳能光伏板风荷载体型系数群体遮挡效应数值模拟研究[J].特种结构,2015,32(3):18-22.
[15] ANDERSON Jr J D. Computational fluid dymanics:the basic with applications[M]. New York:McGraw-Hill, Inc.,1995.
[16] SHIH T H,LIOU W W,SHABBIR A,et al. A new k-ε eddy viscosity model for high Reynolds number turbulent flows[J]. Computers & fluids,1995,24(3):227-238.
[17] PATANKAR S V. Numerical heat transfer and fluid flow[M]. California:Hemisphere Publishing Corporation,1980.

