一种奇异值分解与子空间加权联合的改进MUSIC 算法*
石依山,尚 尚,乔铁柱,刘 强,祝 健
(江苏科技大学海洋学院,江苏 镇江 212003)
0 引言
作为雷达信号处理的重要分支,波达方向(DOA)估计在近年得到了迅速的发展[1],并广泛应用于军事、医学、通信等领域[2-3]。近些年来,超分辨算法逐渐成为主流,其中,最广为人知的是Schmidt 等人在1979 年提出的多重信号分类(MUSIC)算法[4]。
MUSIC 算法的提出推动了超分辨算法的高速发展。在实际应用中,由于通信环境错综复杂,经常存在接收端收到的噪声幅度较大导致信噪比较低或者快拍数不足的情况,此时传统算法的分辨率会有所降低。当存在2 个到达角相近的信源时,两者的谱峰会逐渐相互融合,以至于无法分辨出2 个目标的来波方向[5]。一些学者针对这一问题进行了改进。文献[6]通过对传统算法中的谱函数求导二次之后能在原始波达方向上生成负峰值的特点,利用搜索二阶导数的最小值确定来波方向,而当原谱函数图像并不具有准确的凹凸性时,算法的性能失效。文献[7]将智能优化算法与DOA 估计算法相结合,在可以估计到多个目标的同时降低了搜索时间,但对邻近目标的分辨率不高。文献[8-9]将优化的神经网络运用到DOA 估计中,具有很高的估计精度,但实时性有所欠缺。
本文针对低信噪比、小快拍数情况下传统MUSIC 算法估计性能失效这一问题,提出了一种将最大利用互协方差信息构建矩阵并进行奇异值分解和对改进的子空间进行加权处理相结合的改进MUSIC 算法。相比于常规DOA 估计算法,该算法在基本不提升计算复杂度的基础上,在低信噪比以及小快拍数的条件下对靠近的目标具有较高的分辨概率,在阵元数较少的情况下相较于传统算法分辨概率也有很大提升,具有较高的现实应用价值。
1 阵列信号与经典MUSIC 算法
1.1 一般阵列数学模型
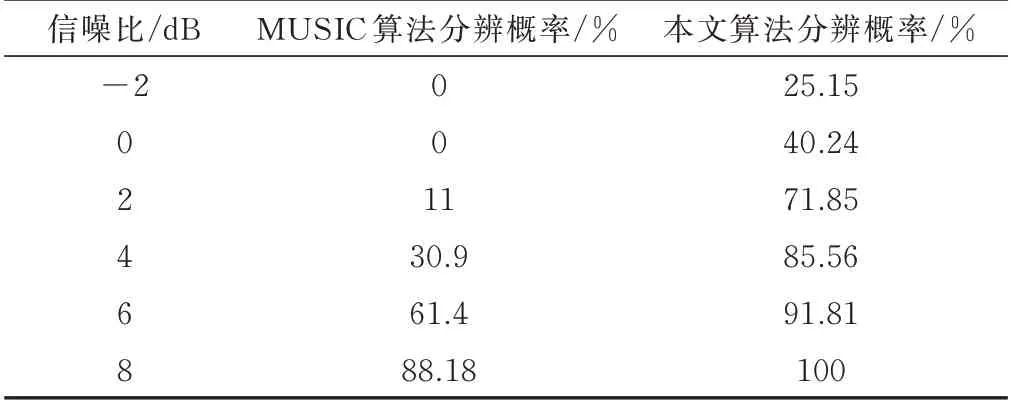
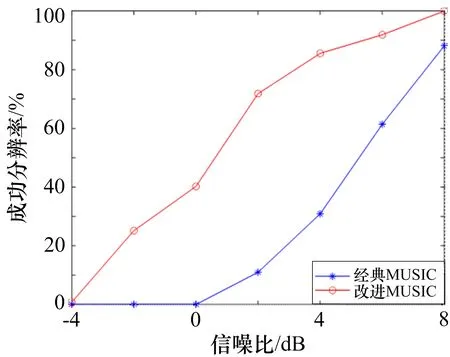
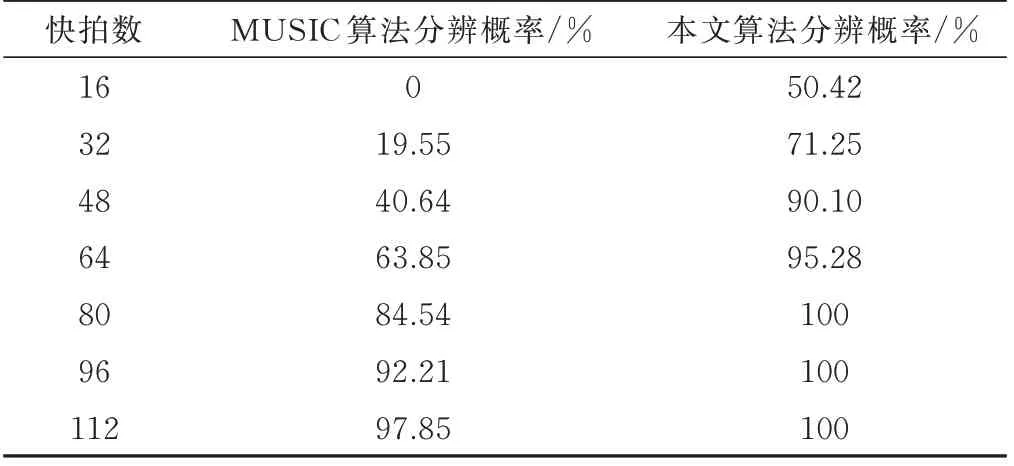
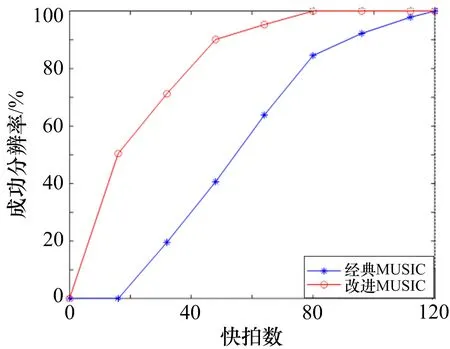
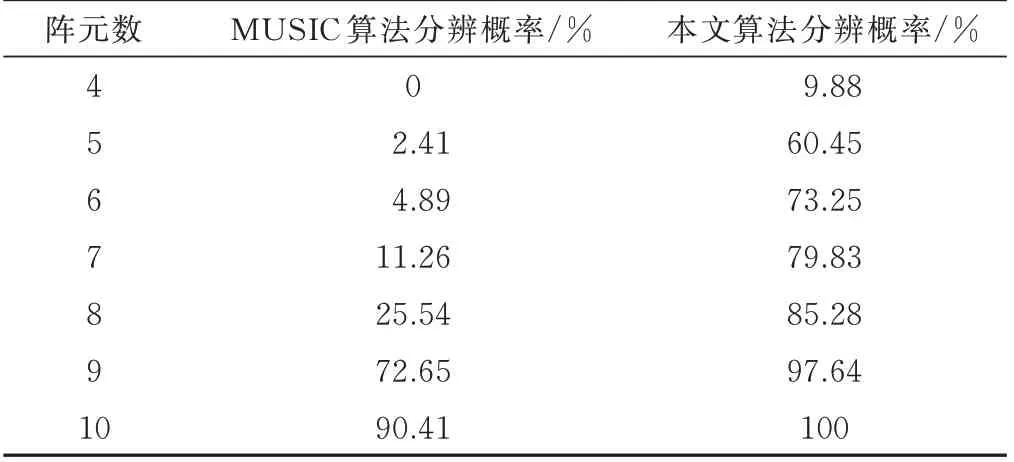
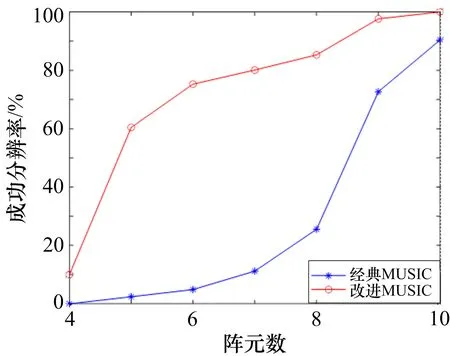
设接收阵列由N个阵元组成,其阵元间距为d,有M(M 式中,A(θ)为N×M维接收阵列流形: 式中,a(θi)为第i个信号的方向矢量: M个入射信号的接收矢量为: N个阵元接收到的高斯白噪声矩阵为: 式中,ni(t)为第i个阵元接收到的噪声,其方差为。 传统MUSIC 算法根据N个接收信号X(t)计算得到协方差矩阵,并将其划分成2 个空间: 在理想条件下,信号子空间与噪声子空间相互正交,即信号子空间中的导向矢量与噪声子空间正交,则有下式成立: 由上述的正交关系,可以得到MUSIC 算法的空间谱函数: 本文提出一种奇异值分解与子空间加权联合的改进MUSIC 算法,该算法分为2 个部分,第一部分对接收信号进行处理,最大程度利用互相关信息构建新的矩阵并利用奇异值分解得到信号子空间和噪声子空间;第二部分充分利用信号特征值和噪声特征值中所包含的信息,分别对信号子空间和噪声子空间进行改进,最终得到一种分辨率高且抗干扰能力强的空间谱估计算法。 本部分对接收数据矩阵进行处理,并提出了最大程度利用互协方差矩阵的信息构建新的协方差矩阵的方法,用以增强改进算法对噪声的抗干扰性,进而提升算法的分辨率。 首先,对接收信号进行如下处理: 式中,Y(t)为处理后的接收信号,X*(t)为X(t)的复共轭矩阵,Z为交换矩阵,其副对角线为1,其他元素均为0,ZHZ=1; 计算X(t)、Y(t)的自相关函数以及两者的互相关函数如下: 为了充分利用互相关信息,这里借鉴前后向平滑(FBSS)技术构建新的矩阵: 如此构成新的矩阵,充分包含了接收信号的自相关信息和互相关信息,对其进行分解得到的子空间受噪声的破坏更小,更加贴合真实值。 式中,vi(i=1,2,…,N)为分解得到的特征向量,它们组成了信号子空间与噪声子空间。 其中信号子空间为: 噪声子空间为: 2.2.1 噪声子空间加权 考虑到噪声特征值未被完全利用这一问题,在信息论准则能正确估计出信源个数的前提下,从大量实验中,可以得到噪声特征值的最大值与最小值之比ξ应满足1<ξ≤2 这一特点[10],这里取ξ=2。由于信噪比降低和快拍数的不足,噪声特征值波动较大,现对噪声子空间做如下改进: 1)构建噪声子空间加权系数: 式中,λi为奇异值分解得到的噪声特征值,α为校正系数。 2)取得噪声特征值的最大值λK+1和最小值λM,若λK+1/λM<2,则校正系数α为0。 否 则 将=λK+1/(λK+1+α) 和=λM/(λM+α)替换式(24)中的λK+1和λM,求出满足不等式的校正系数α。 3)得到校正系数α后,噪声子空间就可以改进为: 式中,vK+1,vK+2,…,vM为噪声特征值对应的特征向量,为改进后的噪声特征值。 如此改进的原理是:将噪声子空间的特征向量进行噪声特征值加权处理,提高了噪声特征值中所含信息量的利用率,并且在噪声特征值被恶劣信号环境所破坏的情况下,也可以通过校正值α约束破坏程度,同时α对信号特征值没有影响,从而确保信源估计不受影响。 于是有: 进而可以得到新的空间谱函数如下: 2.2.2 信号子空间加权 通过文献[11]得知,在信噪比较低、快拍数不足的条件下,由分解接收矩阵获得的信号子空间所受信噪比起伏的干扰相对较小。传统的MUSIC 算法中,信号子空间信息未被利用,这里引入加权信号子空间投影(WSP)算法,该方法对通过特征值分解得到的信号特征值进行取倒数处理,作为信号子空间的加权系数: 将式(24)与式(25)结合,可以有效减少噪声对算法的干扰。 最终,改进后的算法空间谱函数为: 通过对式(26)进行谱峰搜索,即可在对应目标方向位置获得对应谱峰。 为了分析本文提出的改进算法分辨性能,采用实际应用中常见的由8 个阵元组成的均匀线阵进行仿真实验。仿真实验中,阵元间距d=λi/2,接收到的噪声为0 均值的高斯白噪声。 假设2 个远场窄带信号,分别从2°和-2°的方向射向接收阵列,选取经典MUSIC 算法、MMUSIC 算法[12]和本文的改进算法进行比较。在信噪比SNR=0 dB、快拍数等于1 024 时,3 种算法对邻近目标的分辨能力如图1 所示。当信噪比SNR=10 dB、快拍数为112 时,3 种算法对邻近目标的分辨能力如图2 所示。信噪比SNR=0 dB、快拍数等于112 的条件下,3 种算法对邻近目标的分辨能力如图3 所示。 图1 信噪比为0 dB 时的DOA 估计结果 图2 快拍数为112 时的DOA 估计结果 图3 信噪比为0 dB 且快拍数为112 时的估计结果 由图1-2 可以看出,无论是低信噪比还是快拍数不足的非理想条件下,传统MUSIC 算法与MMUSIC算法都无法对邻近目标进行分辨,本文的改进算法在2 个方向之间出现明显的凹陷,成功分辨了两相邻目标。由图3 可以看出,经典MUSIC 算法以及MMUSIC 算法在非理想条件下,来波方向处2 个目标的谱峰已经融合,完全丧失了分辨能力,而本文的改进算法仍可以分辨2 个目标,证明了该算法在强干扰且快拍数不足的条件下仍然具有对相邻目标的分辨性能。 在现实应用场景中,由于噪声的干扰,接收信号的信噪比不够理想,进而导致DOA 估计算法的分辨性能受到影响。假设2 个远场窄带信号,分别从2°和-3°的方向射向接收阵列,快拍数为112,信噪比从-4 dB 到8 dB 以每次2 dB 增长,将本文的改进算法与经典MUSIC 算法相对比,进行200 次Monte Carlo 实验,得到的分辨概率结果如图4 所示,具体数值如表1所示。 表1 信噪比变化时的分辨概率 图4 不同信噪比下改进算法和传统MUSIC 算法的分辨概率比较 如图4 所示,在信噪比较低的条件下,传统MUSIC 算法完全丧失分辨性能,伴随信噪比的提升,本文改进算法的分辨概率迅速增加,分辨性能远高于传统算法,在信噪比为2 dB 时,传统MUSIC 算法还无法分辨目标,而改进算法仍然对目标有较高的分辨率。 在现实应用场景中,常会出现采样次数不足、快拍数较小的情况。假设2 个远场窄带信号,分别从2°和-3°的方向射向接收阵列,信噪比为10 dB,快拍数从16 到112 每次以16 为间隔进行增长,将本文的改进算法与传统MUSIC 算法相对比,进行200 次Monte Carlo 实验,得到的分辨概率结果如图5 所示,具体数值如表2 所示。 表2 快拍数变化时的分辨概率 图5 不同快拍数下改进算法和传统MUSIC 算法的分辨概率比较 由图5 可以看出,伴随快拍数的增大,DOA 估计算法的分辨概率也随之提高。由表2 可得,传统MUSIC 算法在快拍数为96 时具有92%的分辨率,而本文的改进算法在快拍数为48 时,其分辨率可达到90%,改进的算法相较于经典MUSIC 算法的快拍门限降低了48。 作为阵列信号处理的基本组成单元,阵元数量对DOA 估计的结果起到决定性作用,它决定了阵列的接收能力和灵敏度。假设2 个远场窄带信号,分别从2°和-3°的方向射向接收阵列,信噪比为5 dB,快拍数为100,阵元数从4 到10 依次增长,将本文的改进算法与传统MUSIC 算法相对比,进行200 次Monte Carlo实验,得到的分辨概率结果如图6 所示,具体数值如表3 所示。 表3 阵元数变化时的分辨概率 图6 不同阵元数下改进算法和传统MUSIC 算法的分辨概率比较 由图6 和表3 可以看出,阵元的数量对算法分辨率起着重要影响。阵元数由8 变为9 时,经典MUSIC算法的分辨率发生了跳跃式的提升,而改进算法在阵元数由4 变为5 时分辨率就取得了巨大提升,并在6 阵元时已经具备较高的分辨概率。 为了有效克服在低信噪比和小快拍数等的作用下,传统MUSIC 算法分辨率急剧下降的问题,本文给出了一种基于改进的协方差矩阵实现奇异值分解,并对子空间进行了加权的优化MUSIC 算法。该算法充分利用了接收信号的互协方差信息,构建新的协方差矩阵,并通过奇异值分解得到修正后的特征值和特征向量空间,然后通过判断噪声特征值中最大值与最小值之比计算对应的加权系数,并对噪声子空间进行改进;随后引用信号子空间加权算法提高对非目标方向处噪声的抑制能力。仿真结果表明,该算法在传统MUSIC 算法和MMUSIC 算法完全失效的情况下,依然可以分辨出-2°和2°两个相邻目标,具有较高的分辨性能;在低信噪比、快拍数较小以及以及阵元数变化的条件下,相较于传统MUSIC 算法,本文算法在分辨率上有很大提升。■1.2 经典MUSIC 算法
2 改进MUSIC 算法
2.1 奇异值分解方法
2.2 改进的子空间加权算法
3 仿真及分析
3.1 验证算法的分辨能力
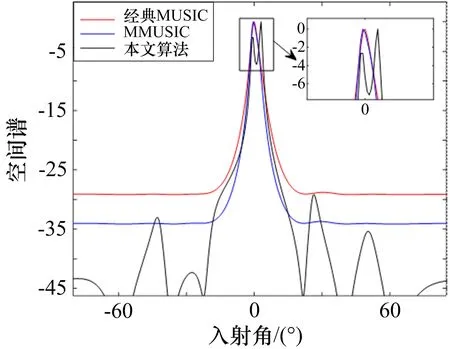
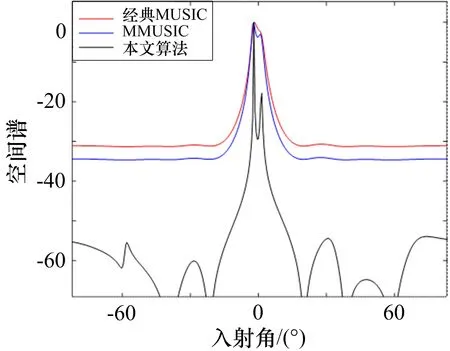
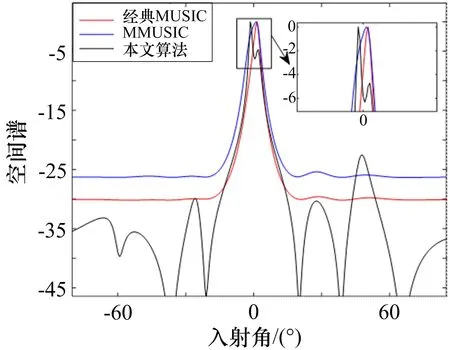
3.2 低信噪对分辨性能的影响
3.3 快拍数对分辨性能的影响
3.4 阵元数对分辨性能的影响
4 结束语

