基于蒙特卡罗方法的混凝土屋面工程防水失效概率算法*

徐洪涛,肖绪文,朱志远,秦 越,霍倩男,卢海陆,朱 彤,周 辉

(1.中国建筑股份有限公司技术中心,北京 101300; 2.中国建筑股份有限公司,北京 100030;3.中国建材检验认证集团苏州有限公司,江苏 苏州 215008; 4.中国建筑第七工程局有限公司,河南 郑州 450004)

0 引言

工程防水涉及多个工种和工序,其理论侧重于材料学[1],在工程中一般遵循经验或采用定性分析[2],工程人员在防水材料与系统研发、工程设计、选型等活动中,可客观指导实践的量化工具很少。

无论是材料防水有效性的试验和判定方法、材料变形,还是变形、老化等因素导致防水失效的模型,都难以计算。材料变形、相互间协同作用的机理复杂,很多计算参数都具有不确定性,完全从数学解析式推导的计算模型可能与实际不符。所以,引入不确定分析方法更可行。

1 研究方法

不确定分析方法适用于输入参数和输出结果。当输入参数不确定时,可基于概率的统计特征计算[3],如贝叶斯理论和马尔科夫链蒙特卡罗模拟方法建立参数统计特征,结合Bootstrap、人工神经网络的概率预测,基于Copula函数的输入参数联合概率分布模型等[4];当采用不确定度表征计算结果时,可用概率分布传递法实现输出量概率分布的解[5]。当不能通过有效的数学模型求解析解时,蒙特卡罗方法(Monte Carlo method,MCM)可通过简单的手段仿真工程随机的工作机制,产生大量数据后以解决实际问题[6]。

理想条件下,屋面防水层的变形取决于邻近材料的直接或间接作用,即协同作用。防水材料的有效性可通过试验得到相对准确值;材料变形可采用热工、力学理论进行计算,准确度高;材料层间的变形协同作用模型则相对困难,界面间的本构关系复杂,可引入不确定度。

结合研究对象的不确定特征,基于文献、工程调研确定变形导致失效的典型部位,归纳材料变形量、变形区间,进行变形量组合计算,引入不确定参数表征变形界面和区间系数,生成满足一定概率分布特征的随机数据,采用MCM计算协同变形量,与材料防水有效性指标进行比较,得出防水失效概率。研究技术路线如图1所示。

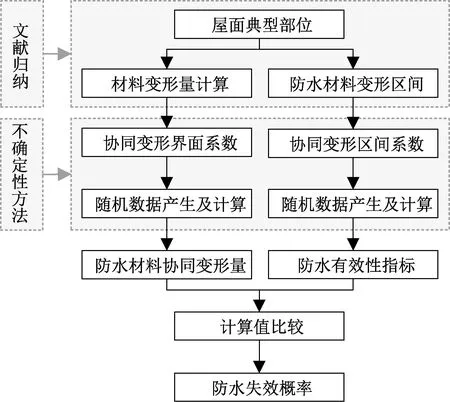
图1 研究技术路线

2 研究内容

2.1 可行性分析

MCM可以通过不确定度或失效概率表征结果。以不确定度表征结果的方法被广泛应用于不确定性的校准中,用于多个输入量和单一输出量的模型[7-8]。胡峰[9]依据试验结果,根据指数分布密度函数计算产品的寿命;赵一帆等[10]指出MCM方法无需考虑输入量相关性、模型非线性的影响,评定复杂模型的不确定度更可靠。计算过程通过输入量Xi的概率密度函数(probability density function,PDF)离散抽样,由模型传递输入量分布,计算获得输出量Y的PDF离散抽样值,进而由输出量Y的离散分布数值得到输出量的最佳估计值,确定不确定度和包含区间,计算过程如图2所示。

图2 以不确定度表征结果方法的计算过程

以失效概率表征结果的方法在建筑领域广泛应用,在已知功能函数与基本变量的概率分布特征时,采用随机抽样并将抽样值代入功能函数,通过大量抽样不断逼近真实失效概率。魏志翔等[11]基于桥梁有限元模型,分析大跨钢管混凝土拱桥构件承载力极限状态下的作用组合值,采用MCM对主要构件可靠度进行分析;杨艳等[12]以砌石重力坝为例,在已知统计参数分布特征的条件下,采用MCM生成随机数代入功能函数,以失效次数和总次数判断失效概率;祁隆等[13]将抗力、截面设定服从对数正态分布,计算结构的可靠性;张隆松等[14]采用MCM计算不同概率分布条件下的基坑变形可靠度。此外,MCM在机械、设备耐久性与可靠度方面也被广泛应用。以失效概率表征可靠度的计算过程是通过数理统计理论中的抽样方法,确定其PDF,获取随机变量样本X1,X2,…,Xi,然后将样本值代入数学函数Y=f(X1,X2,…,Xi)中进行计算,抽样n次后,统计Y失效的次数n′,得到失效概率,计算过程如图3所示。

图3 以失效概率表征结果方法的计算过程

混凝土屋面的材料变形量、防水有效性指标可采用计算或试验得出,而协同变形界面系数、协同变形区间系数可采用不确定度表达,需假定其PDF,采用随机数生成,作为样本参与计算。不确定度表征结果时需包含不确定度和包含区间,解读相对繁琐,以失效概率表征结果则相对直观。综合防水有效性、材料层变形、协同变形量、防水失效概率,可采用MCM建立计算方法。

1)屋面防水失效概率与构造相关,对应屋面构造、防水层的设置、类型、道数等。

2)以不同气候区的温度、湿度、荷载等作为输入参数,采用解析式或有限元建模计算材料层变形量,针对典型部位对变形量进行组合。

3)引入不确定参数,计算防水层受其他材料层变形协同作用,采用MCM方法进行模拟,设定计算次数,判定失效次数,得到防水失效概率。

2.2 防水层协同变形量

材料层变形量可依据现有研究结果,防水层的相对变形量采用最不利条件组合,按部位进行分析。

2.2.1面层相对于保温层变形

屋面面层变形与温度相关,属于周期性变化,保温层初始阶段变形具有一次性特征,防水层会受上侧面层变形和下侧保温层变形的综合影响,如图4所示。

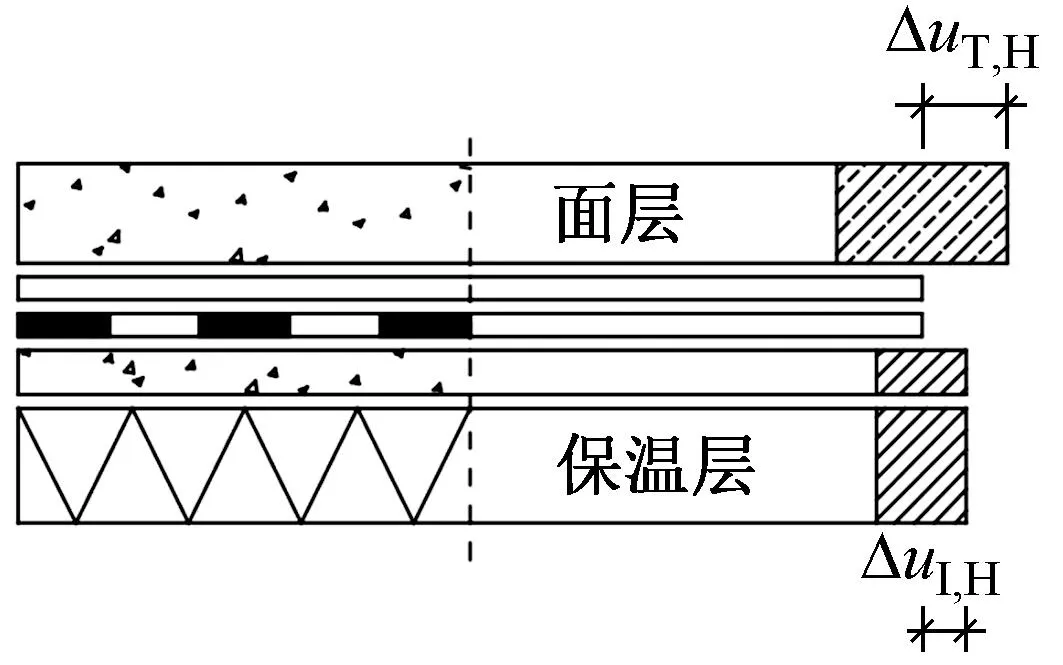
图4 面层相对于保温层变形对防水层的作用

若已知面层变形ΔuT,H、保温层变形ΔuI,H,引入面层对保温层协同变形界面系数γTI-T、保温层对面层协同变形界面系数γTI-I,面层和保温层变形对防水层的协同变形量Δuplane,TI可表达为:

Δuplane,TI=γTI-TΔuT,H+γTI-IΔuI,H

(1)

2.2.2基层相对于保温层变形

屋面基层受外界温度影响相对较小,保温层初始阶段变化具有一次性的特征,防水层会受上侧保温层变形和下侧基层变形的综合影响,如图5所示。

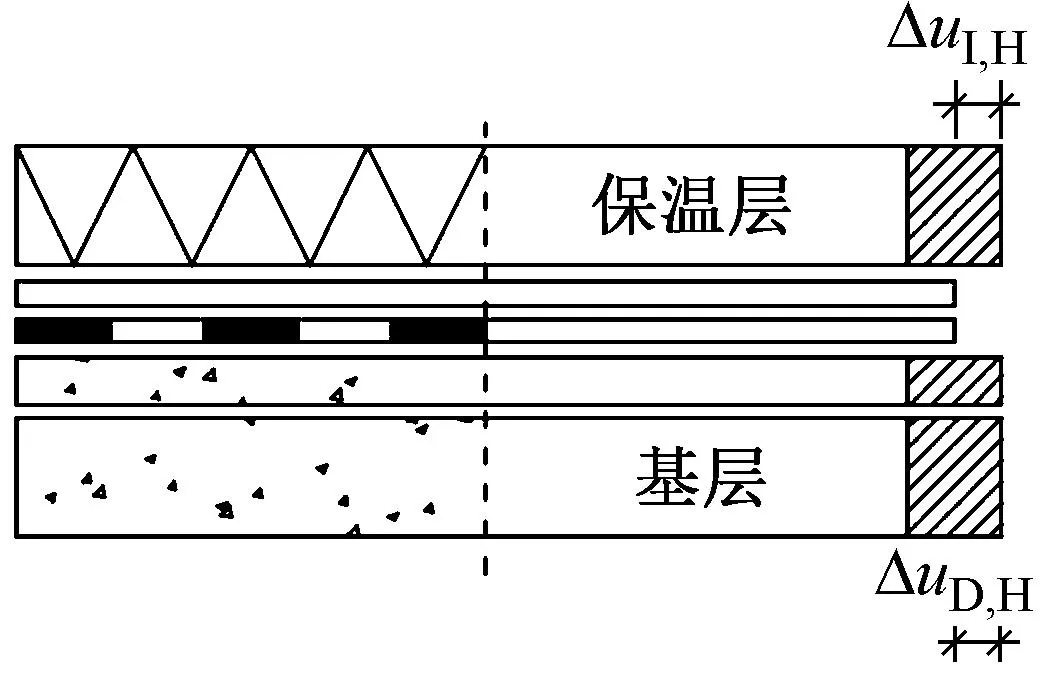
图5 基层相对于保温层变形对防水层的作用

若已知基层变形ΔuD,H、保温层变形ΔuI,H,引入基层对保温层协同变形界面系数γID-D、保温层对基层协同变形界面系数γID-I,基层和保温层变形对防水层的协同变形量Δuplane,ID可表达为:

Δuplane,ID=γID-DΔuD,H+γID-IΔuI,H

(2)

2.2.3女儿墙部位面层相对于保温层变形

女儿墙部位的变形为三维方向,面层、基层在水平方向存在变形,女儿墙在长度方向变形,防水层受到协同变形的作用,可能为拉伸或剪切状态,如图6所示。

图6 女儿墙部位面层、保温层变形对防水层的作用

面层变形取影响较大值,若已知面层变形ΔuT,H、保温层变形ΔuI,H,引入面层对保温层协同变形界面系数γPT-T、保温层对面层协同变形界面系数γPT-I,当面层变形与女儿墙的变形垂直时,防水层受拉伸和剪切综合作用,面层和保温层变形对防水层的协同变形量Δuparapet,PT,tensile可表达为:

Δuparapet,PT,tensile=

(3)

若面层变形与女儿墙的变形方向平行,防水层主要受剪切作用,面层和保温层变形对防水层的协同变形量Δuparapet,PT,shear可表达为:

Δuparapet,PT,shear=γPT-TΔuT,H+γPT-IΔuI,H

(4)

2.2.4女儿墙部位基层相对于保温层变形

基层温度条件相对稳定,女儿墙部位受外界温度影响更明显,主要变形来自于保温层和女儿墙基层,如图7所示。

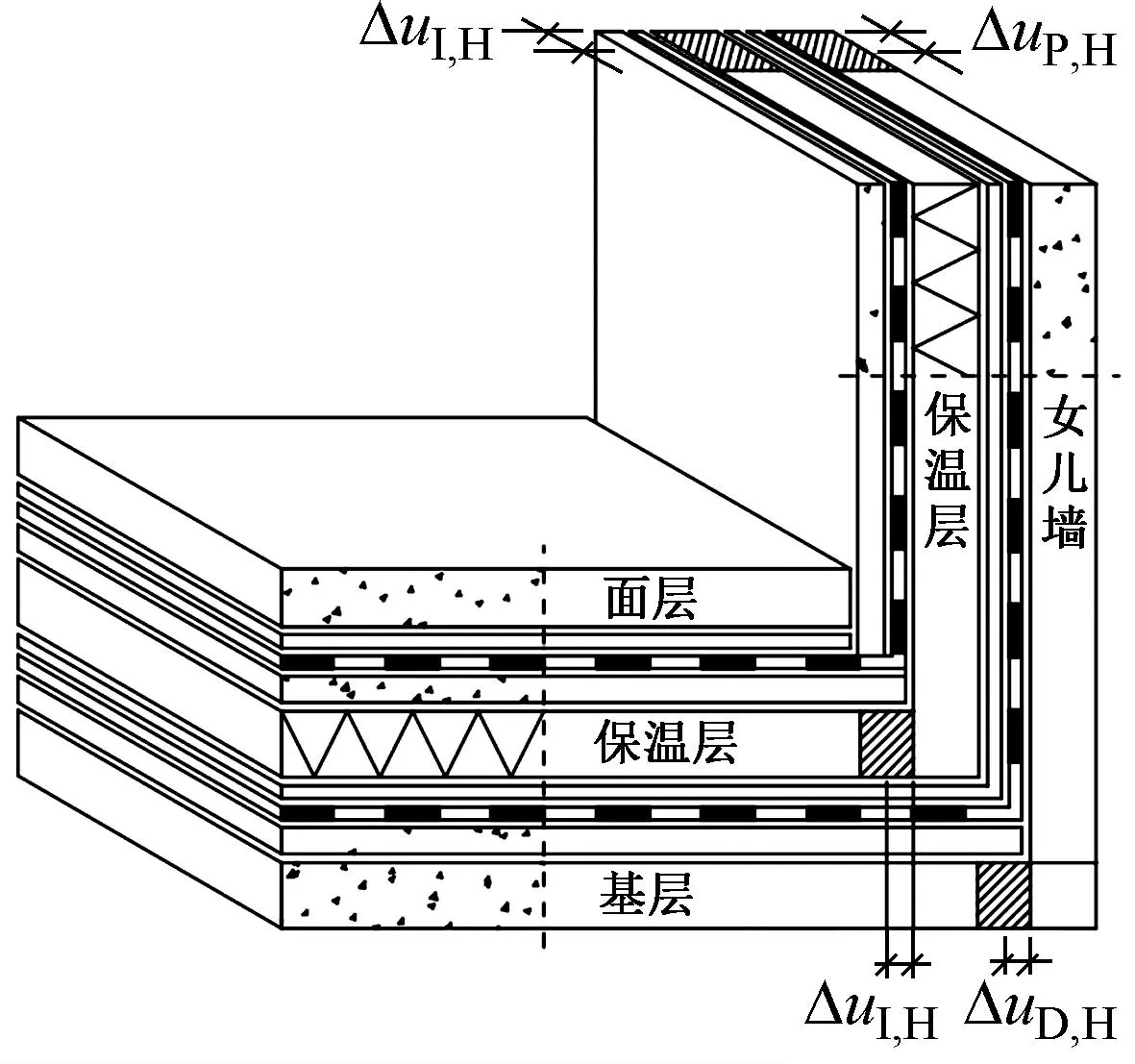
图7 女儿墙部位基层、保温层变形对防水层的作用

基层与女儿墙变形按照变形方向取影响较大值,若已知基层变形ΔuD,H、保温层水平方向变形ΔuI,H、女儿墙变形ΔuP,H,引入基层对女儿墙协同变形界面系数γPD-D、保温层对女儿墙协同变形界面系数γPD-I、女儿墙对基层协同变形界面系数γPD-P,假设基层变形与女儿墙的变形垂直,防水层受拉伸和剪切综合作用,Δuparapet,PD可表达为:

Δuparapet,PD=

(5)

女儿墙部位的变形协同作用相对复杂,防水层在受剪切或拉伸作用时,其实际变形与试验室防水材料有效性试验模型可能不一致,有待进一步研究。

2.2.5多层防水层协同变形

当有2层或3层防水材料叠合时,防水材料间的协同变形也存在不确定性,可依据材料之间的结合特征,引入防水材料间协同变形界面系数γM-M参与计算。

2.3 防水有效性判定

在引入不确定度协同变形界面系数γi后,可得出防水材料的协同变形量,为评判材料防水有效性,需确定防水层变形量Δu是否在防水有效性的范围内,可引入变形区间尺寸LTEN,LTEN是一个不确定值,可采用协同变形阈值LLim和协同变形区间系数γj表达:

LTEN=LLimγj

(6)

在确定Δu和LTEN后,防水材料的协同变形延伸率δ可表达为:

(7)

在得到Δu或δ后,可对Δu与ΔuFailure进行比较,也可用δ与防水有效性δi,Failure进行比较,以判定防水层因协同作用变形后,是否能有效工作,其判定条件C为:

C=Δu-ΔuFailure

(8)

C=δ-δi,Failure

(9)

2.4 防水失效概率

判定条件C即屋面防水有效性。当防水层位于保温层、结构层上部时,上部防水层不允许失效,否则将导致保温失效,或在屋面内部存水;多层防水层叠合使用时,当多层防水层均出现失效时,才判定失效。

采用MCM方法模拟,一般可取104～106组输入量计算[8],得到相应的输出值数量MC,Total,依据判定条件C统计失效输出值数量MC,Failure,得到相应部位的失效概率P:

(10)

如果防水层叠合使用,各层防水层是否失效概率Pi为独立事件,所以失效概率P为:

(11)

2.5 不确定参数分析

防水层受邻近材料协同变形作用与固定方式、压力、界面、相邻材料类型等影响,所引入的协同变形界面系数γi取决于以下条件。

1)完全同步变形 当相邻材料联系紧密,或通过机械固定方式连接时,材料变形会完全作用在邻近材料层上,此时γi偏向于1,如通过钢筋连接的混凝土构造柱、刚性连接等。

2)部分同步变形 相邻材料通过摩擦力或内聚力作用,传递变形量,部分同步变形可能导致邻近材料的变形不均匀,γi∈(0,1)。

3)完全不同步变形 相邻材料之间通过摩擦力作用,但摩擦力有限,此时γi偏向于0,如界面间设置了缓冲层或隔离层。

如果假定协同变形界面系数γi服从“概率分布已知”的条件,在进行协同变形研究时,将γi作为输入量,可依据试验数据、专家判断等方式确定PDF[7]。如果假定协同变形界面系数服从“概率分布已知”,其关键在于假定的概率分布是否与实际一致,这是决定最终计算结果准确度的关键。为了最大程度接近PDF的正确性,可先对各类γi进行排序,依据其相互之间的比较关系设定PDF。

3 讨论

3.1 不确定参数假定概率分布已知

MCM方法中,不确定参数的分布特征是计算的关键。如果选取假定概率分布已知,可快速采用MCM计算,无论是材料还是构造的改变,其计算内核均为同一模型。所以,界定屋面材料、构造后,只要假定的PDF基本符合实际,就可将构造、材料、气候区等影响防水可靠度的因素置于同一个平台进行对比分析,以量化的结论对比,得出定性的结论。不确定参数包括协同变形界面系数γi、防水材料间协同变形界面系数γM-M和协同变形区间系数γj。

如果材料变形对防水层产生明显作用,如屋面基层变形对邻近防水层的作用、女儿墙基层对邻近防水材料的作用,这些界面材料主要以熔接、粘贴、黏附、机械等方式连接,拟取指数分布,分布区间为(1,0)。

如果材料变形对防水层的作用不确定,如屋面面层与防水层、保温层与防水层等,这些部位通过摩擦力传递,拟取正态分布。

如果材料变形对防水层的作用不明显,界面的荷载有限,变形的相互作用或影响有限,如隔离层、空铺的防水层,或层间摩擦力较低的保温层与防水层,拟取指数分布,区间为(0,1)。

当多层防水层叠合时,如卷材类、薄片类材料,材料间相对独立,拟取指数分布或正态分布,区间为(1,0)。

3.2 不确定参数概率分布未知

在第2.5节假定协同变形界面系数γi的PDF可知,而实际中γi可能没有解析式,其概率分布未知。如采用Copula函数,可将一维边缘分布与多维分布联系,生成联合分布。利用边缘分布信息,可从实际中观察主要的边缘分布状况,选择合适的Copula函数类型,拟合现实数据,最后确定Copula函数中的待定参数,得到联合概率分布。采用Copula函数,可采用小样本确定研究对象的参数多维分布模型[4]。

对于混凝土屋面工程而言,也可参考Copula函数确定协同变形界面系数γi,在实验室中采用小模型模拟实际场景,通过试验观察材料变形对界面材料的影响,以试验数据作为样本的函数[15]。

4 结语

通过对MCM进行可行性分析,基于防水层协同变形量和材料防水有效性指标,引入不确定参数,建立防水失效概率计算方法,得到以下结论。

1)进行混凝土屋面工程的量化分析时,很多参数都具有不确定性,适合引入不确定参数形成量化计算模型。

2)混凝土屋面防水有效性量化指标可采用防水失效概率表征。

3)基于MCM的防水失效概率计算方法,无论不确定参数的PDF已知或未知,均可建立相对客观的算法,在此基础上对量化结果进行对比,可得出相对客观的结论,适于工程分析。

不同的工程部位、构造,其失效机理存在较大差异,材料层间的协同变形可结合试验,以确定不确定参数已知或未知的PDF,防水有效性指标也需通过更多的试验确定。