混凝土屋面工程材料层变形与协同作用*

徐洪涛,肖绪文,朱志远,刘 星,秦 越,霍倩男,朱 彤,周 辉

(1.中国建筑股份有限公司技术中心,北京 101300; 2.中国建筑股份有限公司,北京 100030;3.中国建材检验认证集团苏州有限公司,江苏 苏州 215008; 4.中国建筑土木建设有限公司,北京 100073)

0 引言

我国建筑工程大量采用钢筋混凝土屋面,屋面渗漏长期困扰用户。2020年对全国建筑渗漏调研显示[1]:按建筑渗漏部位,屋面渗漏比例最高,占比30%;按不同气候区,东北与华中地区渗漏率最高,超过73%,西北、西南、华南地区渗漏率较低,为36.6%～41.9%。可以看出,屋面渗漏与气候条件存在关联,气候区划分的基础指标为温度、湿度[2],材料因其作用或自身特性而老化、变形,进而导致防水材料失效[3]。

混凝土屋面材料一般以层状方式组合,防水层受邻近材料变形协同作用的机理是屋面防水有效性研究的基础。

1 研究方法

屋面防水层失效一般体现为老化和变形的综合作用[4],老化是自然衰减过程,变形来则源于其他材料层变形的作用,不同材料层之间存在变形的相互作用效应,即协同作用。屋面材料受温度、湿度、荷载导致变形的理论和试验研究相对丰富,如有限元计算温度变形和应力分布已被广泛使用,基于约束理论计算材料层间变形也相对可靠[5]。

材料变形适合借鉴已有的理论和方法,而材料层间的协同作用研究相对较少,其本构关系很难确定[6],可针对混凝土屋面典型部位,按构造对变形量进行组合,引入不确定参数表征协同作用。研究技术路线如图1所示。

图1 研究技术路线

2 研究内容

2.1 变形部位调研

混凝土屋面防水失效常出现在一些典型部位,采用德尔菲问卷调研的渗漏部位结果如图2所示。调研邀请了10位防水领域不同专业的专家,结果具有一定的代表性。

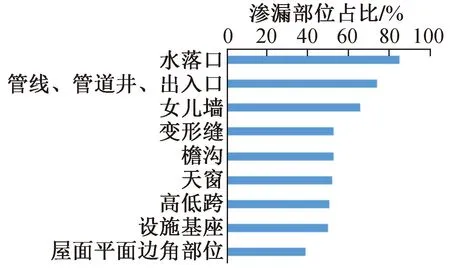
图2 混凝土屋面渗漏部位占比

屋面防水有效性取决于材料变形与防水材料有效性,表征材料防水有效性的指标与变形率、协同变形尺寸相关,为了对材料变形与防水材料进行关联,需确定混凝土屋面的典型变形部位,调研结果如图3所示。

图3 混凝土平屋面可见变形调研

依据现有研究、问卷和现场研究,可将屋面平面和女儿墙部位作为典型部位开展研究[7]。

2.2 变形计算规划

导致材料变形的因素主要为环境条件和材料本体,为便于计算,将材料、组件作为相对独立单元进行分析。

材料变形一般包括初始变形,温度、湿度及荷载作用变形。初始变形主要来自于施工过程,结构部分可假定为稳定状态,面层、保温层的初始阶段变形会对防水层产生影响。温度、湿度作用会反复循环,是导致变形的主要因素,混凝土屋面各层材料均会受其影响,同时受邻近材料或结构的约束。温度、湿度的变化为耦合关系,可做简化处理。保温层或密度较低的材料,在使用中受荷载作用存在蠕变。变形产生的应力一般在形状发生变化处释放,如女儿墙、屋面转角等部位。结合混凝土屋面变形的部位、材料层及变形类型,计算规划如表1所示。

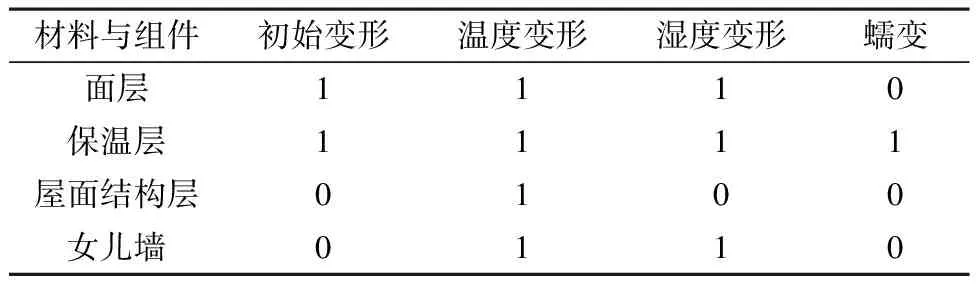
表1 材料变形计算规划

2.3 材料层变形

2.3.1初始变形

混凝土初始变形碱骨料反应的裂缝小于1%,主要出现在表层,一般由水分蒸发引起,开裂程度较小。初景峰等[8]对不同材料和养护时间进行组合,通过试验得出最大裂缝宽度;关彦斌等[9]研究了混凝土早期裂缝,其塑性收缩裂缝的宽度为1～5mm。由于初凝阶段材料处于塑性状态,对其他材料的影响有限,可不考虑。

在自收缩和干燥收缩阶段,材料强度逐渐形成,需考虑对邻近防水层的影响。Brooks[10]对混凝土的收缩进行了分类,分成了塑性收缩、膨胀变形、碳化收缩、干燥收缩和自收缩。EN 1992混凝土规范中,混凝土的收缩率Sca与其强度呈线性关系,假定防护层C25混凝土强度28d达到100%,则Sca=11×10-6。在BS 1881—5:1970中有相应的计算建议[11],在50%RH(相对湿度)时,28d干燥收缩率Scd=400×10-6,90dScd=750×10-6,365dScd=850×10-6。计算时可取初始时间段为3个月,初始阶段水平方向收缩值ΔuIH,Top为防护层长度Lcs与干燥收缩率Scd的乘积:

ΔuIH,Top=LcsScd

(1)

保温层初始阶段的变形主要来自于荷载作用,可设定保温材料在承载力范围内为弹性变形[12-14],依据荷载值和弹性模量EIns、厚度TIns进行计算,得出保温材料竖向变形量ΔuIns,IV:

ΔuIns,IV=EInsTIns

(2)

2.3.2温度变形

屋面的温度与气候区、朝向、表面特征等相关[15],主要取决于气候区[2]。屋面各材料层的年度温度极值、波动可精确计算[16],由温度导致材料层间的变形可采用有限元计算[17-18],也可采用解析式计算[2],相应的理论与算法较成熟。熊小林[17]采用ANSYS软件分析某23层公寓100m长楼盖温度应力,取温差为25℃,由于约束的存在,结构变形相对有限。胡显燕等[18]采用ANSYS软件计算90m × 45m现浇楼盖结构季节温度波动效应,由于结构的约束,变形最大部位发生在顶层,最大凸起部位出现在屋面边缘,相对而言,这一模拟结果更接近实际。有限元模拟分析可揭示混凝土屋面在温差条件下的宏观变形,微观的协同变形机理还需探索。

国内关于屋面板温度应力导致裂缝的研究,多参考王铁梦“长墙及地基板的温度收缩及应力”理论。何祥国等[19]以混凝土屋面板和墙体相互约束为边界条件,得到屋面板与砖砌体的温度应力及裂缝计算表达式。姜文正[7]针对框架顶层墙顶与屋面梁底交界裂缝,建立了温差作用下的应力计算表达式。根据相关研究对“长墙及地基板的温度收缩及应力”理论的诠释,当相邻材料层之间变形值不一致时,由于接触面之间存在摩擦力或内聚力,基于约束理论,推导建筑不同组件间应力与应变的解析式:任意点的位移由约束位移与自由位移组成,如果已知温差ΔT、材料层厚度H、长度L、弹性模量E、温度线性膨胀系数α,引入的界面阻力系数CX、裂缝宽度修正系数φ和综合计算系数β;其中,界面阻力系数CX是一种经验值,与界面材料性能、接触面积、压力等相关,综合计算系数β取决于界面阻力系数CX、材料厚度H和弹性模量E。则材料层温度变形ΔuT计算如下:

(3)

式(3)的推导过程从一维杆件开始,避开了其他方向的约束,实际材料会受各个方向的约束,当材料层体积较大时,还与自身约束相关,此后采用温度应力光弹试验实证[20],试验结论显示与计算值存在偏差,如端部区域。即便如此,该解析式用于一维方向分析时,如长条墙体、基础、长宽较大的板状结构等,理论推导相对合理,是一种简单易用的工程方法[21]。

有限元方法计算可更接近实际工况,关键参数为材料层协同变形的本构关系,还待进一步研究。

2.3.3湿度变形

材料在同等绝对湿度条件下,温度升高会降低相对湿度,所以热膨胀往往和湿膨胀成反向关系,工程计算中多以温度为主导因素。材料含湿率与变形的研究主要以中小型试样研究为主。

水泥基材料的变形与含水率之间为非线性关系,在20℃条件下,相较于从65%RH到完全浸水状态,从65%RH到绝对干燥这一阶段的收缩更显著,实际环境升温接近于从65%RH到绝对干燥这一阶段[22]。针对硅酸盐类砌块材料,吕春飞等[23]对A5.0蒸压加气混凝土砌块的变形研究显示,早期含湿量变化和收缩值非常快,后期逐渐平缓,吸湿曲线具有对数增长的特征。易晓园等[24]研究表明:当砌块温度达到环境温度后,温度变形十分微小,主要以干燥收缩变形为主。Mauroux等[25]研究了抹面砂浆干燥导致的微裂,Erich[26]和Helmut[27]在早期对砂浆含湿率与收缩关系的研究均显示砂浆从完全干燥到65%RH含湿率时变形较大。

水泥基材料的冻融变形可用Setzers微冰晶成长模型解释[28],经过冻融循环后,水泥基材料热膨胀系数会因材质的破坏而降低[29]。冻融后材料抗拉强度降低,对邻近材料约束降低。

综合以上研究,简化的湿膨胀计算可综合材料长度L、含湿率膨胀系数δ、年均最大相对湿度差Δφ,无机类材料的湿度变形ΔuRH计算如下:

ΔuRH=LδΔφ

(4)

此外,保温材料可能由于熟化不够,使用过程中会产生变形,如肖军[30]对挤塑聚苯板XPS在没有约束条件的试验显示,受温度、湿度影响会出现较大变形。考虑屋面其他材料的约束,材料熟化可视为一次性变形,可引入定值ΔuRH,Ins参与计算。

2.3.4压缩蠕变

蠕变主要来自于保温层。颜熹琳等[31]研究了PUR泡沫塑料在荷载、高温、高湿的作用下,压缩强度会出现约8%的下降。王一临[32]对EPS泡沫塑料压缩蠕变性能的研究表明,在压缩状态时,微孔结构易受损伤,蠕变随时间的推移以指数规律衰减。李慕珂等[33]对PUR泡沫塑料在不同温度、应力下的蠕变研究显示,初始阶段材料表现为弹性形变,蠕变量和时间呈线性关系,蠕变速率较高;随着时间的推移,变形由弹性形变转入弹塑性形变,高温时蠕变程度更大,应力和温度是影响蠕变的重要因素,可采用Modified Time Harding模型建立本构方程。魏轩等[34]对常温和不同应力下PUR泡沫塑料的压缩蠕变研究显示,压缩蠕变过程分为两个阶段:第1阶段蠕变速率随时间延长而逐渐降低,第2阶段的蠕变速率基本保持恒定,可采用Burgers模型得到本构模型。简易计算可采用相应标准中的参数[12-14]保温层厚度HIns、蠕变系数CIns计算得出蠕变量ΔuCreep,Ins:

ΔuCreep,Ins=HInsCIns

(5)

2.4 变形组合

单一材料的变形可理解成相对于其他材料的位移,工程中可采用简易方法对变形量进行组合。

面层包含初始变形、温度和湿度变形。初始变形具有不可逆性,需参与计算,温度、湿度变形不能直接叠加,两者具有耦合关系,可取较大值。3类变形分别属于不同阶段,按水平和垂直方向分别计算。水平方向变形主要受湿度影响,可不考虑初始变形和蠕变;垂直方向需考虑初始变形和蠕变影响。基层水平方向变形主要受温度的影响。

女儿墙与材料类型相关,一般为混凝土或砌块,取温度、湿度变形值的较大值。

综上所述,材料层间的相对最大变形量如表2所示。

表2 材料层间相对最大变形量

为了将材料变形及对防水层的协同作用形成关联,可选取典型构造,考虑主要变形的材料层,对单一部位建立模型进行分析,如图4所示。

图4 屋面协同变形计算部位示意

典型部位包含平面和女儿墙,协同作用变形取邻近材料层的相对位移,变形量组合如下。

1)平面部位面层相对于保温层(top-insulation)变形量Δuplane,TI取决于面层变形ΔuT,H和保温层的水平变形ΔuI,Ins,H:

Δuplane,TI=f(ΔuT,H,ΔuI,Ins,H)

(6)

2)平面部位基层相对于保温层(insulation-deck)变形量Δuplane,ID取决于基层变形ΔuD和保温层水平变形ΔuI,H:

Δuplane,ID=f(ΔuD,H,ΔuI,H)

(7)

3)女儿墙部位面层和保温层变形相对对防水层(parapet-top)的拉伸变形量Δuparapet,PT,tensile和剪切变形量Δuparapet,PT,shear取决于面层变形ΔuT,H、保温层变形ΔuI,H:

Δuparapet,PT,tensile=f(ΔuT,H,ΔuI,H)

(8)

Δuparapet,PT,shear=f(ΔuT,H,ΔuI,H)

(9)

4)女儿墙部位相对于基层(parapet-deck)变形量Δuparapet,PD取决于屋面基层ΔuD、女儿墙变形ΔuT,H与保温层变形ΔuI,H,ΔuI,V:

Δuparapet,PD=f(ΔuD,H,ΔuI,H,ΔuI,H,ΔuI,V)

(10)

2.5 变形协同作用

从局部对防水层变形进行分析:如果与防水层相邻材料的相对位移为Δui,防水层变形量Δu会与Δui之间存在一定的比例关系,可引入协同变形界面系数γi,γi描述了邻近材料形变作用于防水层,导致其形变的程度,防水层变形量Δu计算如下:

Δu=Δuiγi

(11)

为了判定防水材料的有效性,引入防水材料协同变形延伸率δ和变形区间尺寸LTEN,考量其是否在有效范围内,变形区间尺寸LTEN是不确定值,采用协同变形阈值LLim和协同变形区间系数γj表达:

LTEN=LLimγj

(12)

在确定防水层变形量Δu和变形区间尺寸LTEN后,防水材料的协同变形延伸率δ可表达为:

(13)

相邻材料的相对位移Δui、防水层变形量Δu及变形区间尺寸LTEN的关系如图5所示。

图5 邻近材料变形协同作用

得到防水层变形量Δu或协同变形延伸率δ后,可对防水层变形量Δu与允许变形量ΔuFailure进行比较,也可用延伸率δ与允许延伸率δi,Failure进行比较,以判定防水层是否有效,其判定条件C为:

C=Δu-ΔuFailure

(14)

C=δ-δi,Failure

(15)

其中,允许变形量ΔuFailure为允许延伸率δi,Failure与变形区间尺寸LTEN的乘积,允许延伸率δi,Failure通过试验确定。

3 讨论

3.1 防水层变形量与有效性

计算变形量时,需将屋面作为整体考虑,实际工程的变形复杂,无论是解析式、有限元还是试验,都与实际存在一定的偏离。理论计算一般只考虑单一因素或主导因素,如温度作用,实际工程中的温湿度耦合、材料变形、荷载引起的变形远比理论复杂。

一般而言,柔性防水材料的允许变形量ΔuFailure远超屋面材料实际变形量,实际变形可能位于极小的尺寸范围内,类似于“微位移”变形,即变形区间尺寸LTEN很小。实际工程的基层、保护层、面层的变形不均匀,且变形方向不确定,需引入不确定参数。

3.2 协同作用

材料防水有效性指标允许变形量ΔuFailure或允许延伸率δi,Failure较难界定,且防水材料与其他材料之间的协同变形很难精确计算,邻近材料变形后的协同作用,很难建立有效的模型,因为界面的物理、化学结合程度、摩擦力等因素均存在不确定性。引入不确定参数,可将问题简化,包括变形界面系数γ和变形区间尺寸LTEN。

协同作用的机理复杂,如果可揭示典型部位的协同作用机理,如基层、找坡层、找平层、保护层、面层变形后的集中释放,也可从构造层面提出减少开裂的措施。

4 结语

通过梳理混凝土屋面材料层的变形量计算方法,及分析变形协同作用,得到如下结论。

1)防水层变形值会受邻近材料的协同作用,变形量计算是开展防水有效性研究的基础之一,可选择主导因素,以试验、解析式、有限元等方式得到。

2)材料层变形的协同作用可引入不确定参数,包括协同变形界面系数与协同变形区间系数,计算出变形量、延伸率等防水有效性关键指标。

屋面防水层受其他材料变形协同作用的关键在于材料层之间的本构关系,可采用试验得到,也可引入不确定参数,这是后续研究的重点。