基于真实数据反演的风扇转子本机平衡方法

陈立芳，孙亚冰，*，周书华，高强，乔保栋，李栋

1.北京化工大学 发动机健康监控及网络化教育部重点实验室，北京 100029

2.北京化工大学 高端压缩机及系统技术全国重点实验室，北京 100029

3.中国航发沈阳发动机研究所，沈阳 110015

风扇转子往往工艺平衡状态良好，但工作状态时不平衡振动依然较大，需在发动机试车台上进行本机平衡［1-5］。当前，涡扇发动机风扇转子本机平衡多采用三圆法［6-9］进行，通过3 次试重获得不平衡量，至少5 次启停车完成风扇转子本机平衡，虽抑振效果良好，但启停次数过多使得动平衡效率低且成本高。

此外，航空发动机研究院所也经常采用影响系数法进行风扇转子本机平衡。姜广义等［10］采用叶片检测系统测量定制磁钢的键向信号，一次试重即获得了配平大小和方位，实现了低速（3 000 r/min 左右）下的风扇转子本机平衡。然而实际工作中，机匣振动经复杂路径传递会导致影响系数稳定性差，往往需要增加试重次数。而且，发动机各机台间动力学特性差异较大，测得的影响系数难以推广应用。

虚拟动平衡法通过仿真构建与实际转子和参数相符的动力学模型，在模型上添加虚拟激励获得响应，计算影响系数进行动平衡的方法。目前，该方法基于键向信号可以实现无试重虚拟动平衡［11-16］。宾光富等［17］在汽轮机模拟试验台上进行过有效验证，王维民等［18］在离心式氨气压缩机上也有成功应用。结合粒子群寻优算法，陈立芳等［19］提出一种基于无键相虚拟动平衡方法，在有限元模型基础上利用粒子群算法寻优转子不平衡量，通过最多2 次试重完成动平衡，试验台测试抑振效果显著。但以上方法均对模型的精度要求高，难以应用在具有薄壁机匣复杂结构的航空发动机风扇转子上。

因此，针对航空发动机风扇转子本机平衡的重大需求，本文结合反演理论和虚拟动平衡方法，提出一种启停次数少，无需键相信号、能匹配不同机台动力学特性的本机平衡方法。本方法融合转子动力学和数据反演理论，通过分析风扇转子振动传递路径明确动刚度特征参数，基于模型和动平衡数据提取机台的动力学特征参数信息，建立对应机台反演特征参数库用于计算转子不平衡量。本文的创新之处在于，有效利用发动机现场平衡数据，提高动平衡效率。

1 反演理论和风扇转子反演模型

1.1 反演理论

反演模拟原理［20-21］是将一个物理系统抽象为一个数学上的参数化模型，利用可测参数的某些实测结果推断模型参数的真值。系统被参数化后，模型可用一组参数来表达，模型参数所构成的空间称为模型空间M={mi}，可直接观测数据构成数据空间D={di}。在实际反演问题中，根据D中的观测数据反推M中的待求参数［22］。如果系统为一线性系统，则相应模型可用线性矩阵方程表达，可将其表示为

通过广义求逆可得模型不可测参数的解，将其表示为

式中：D为模型可测参数；M为模型不可测参数；G为相关系数矩阵；G-1为广义逆矩阵。

虑及在风扇转子动力学问题中，无法直接测量转子的不平衡量U，而能直接观测的是由不平衡量U产生的振动响应X。因此，可根据反演理论，以多转速下的转子不平衡量U作为模型中的待求参数，振动响应X作为可观测数据，构建风扇转子振动系统的参数化模型，可为其他相似机台的转子不平衡量求解提供技术参数支撑。

1.2 构建风扇转子反演模型

由于风扇转子结构复杂，振动测点通常布置在进气机匣表面。根据转子动力学理论将风扇转子振动传递系统描述为转子-轴承-机匣系统，发生在风扇转子上的不平衡振动经轴承（支点1）传递到机匣，振动传递系统及路径分解如图1所示。

图1 风扇转子振动传递系统及路径分解Fig.1 Fan rotor vibration transmission system and path decomposition

为获得反演特征参数，根据激励与响应之间的相互关系，分解振动传递路径，提出风扇转子振动传递过程中的4 个动刚度参数：

式中：Kcs为机匣到轴承支点1 的动刚度；Fs为支点1 的力；Xc为机匣的上测点的振动位移；Ksd为支点1 到风扇转子动平衡平面的动刚度；Fd为转子上的不平衡力；Xs为支点1 的位移；Kss为支点1到支点1 的动刚度；Kcd为机匣到风扇转子动平衡平面的动刚度。

根据“动平衡平面（d）-支点1（s）-机匣（c）”的振动传递关系可得：

上述动刚度参数结合数据反演原理可构建风扇转子振动传递系统的参数化模型如图2所示。以多转速下的不平衡量U={Ui}为待求模型参数，机匣振动位移X={Xi}为可观测量。动刚度Kcd、Ksd、Kss和Kcs为可计算模型特征参数。

图2 风扇转子振动系统参数化模型Fig.2 Parametric model of fan rotor vibration system

2 真实数据反演的本机平衡方法

2.1 建立风扇转子有限元模型

根据某型涡扇发动机风扇转子真实结构建立有限元模型。建模原则：一、二、三级叶片用等质量和等转动惯量的刚性盘单元表示；忽略倒角、螺纹孔等结构特征；支点1 和支点2 用轴承单元表示，假设支承刚度各向同性，无交叉刚度和阻尼［23］；集中质量作用处、轴径变化处、轴承支承处均确保有单元节点，如图3所示：轴单元238个，盘单元3 个，轴承单元2 个，共243 个单元。其中支点1 位置为8 号节点，支点2 位置为102 号节点，试重位置为11 号节点。

图3 风扇转子有限元模型Fig.3 Finite element model of fan rotor

2.2 基于实测临界转速优化模型

临界转速是转子动力学特性的重要表征参数，其中支承刚度对临界转速的影响最大［24-27］，利用机台的实测临界转速对支承刚度进行优化以提高风扇转子有限元模型与实际机台的匹配度。

首先，确定模型优化的目标参数。基于模型进行临界转速分析，探究支点1 和支点2 支承刚度对临界转速的影响规律。考虑到临界转速裕度需大于20%，因此，以支点1支承刚度2.2×107N/m，支点2 支承刚度1.0×108N/m 为基准值，支承刚度变化范围为正负基准值的1/2，每次固定一个支点刚度，展开前三阶临界转速分析，如图4所示。

图4 两支点支承刚度对临界转速的影响Fig.4 Influence of two support stiffness on critical speed

由图 4（a）可见，支点1 支承刚度可有效调节一阶临界转速，对二阶临界转速影响不大，对三阶临界转速有一定的调节效果；由图 4（b）可见，支点2 支承刚度对一阶临界转速影响不大，对二阶临界转速几乎无影响，可有效调节三阶临界转速。对比可知，支点1 的支承刚度对一阶临界转速影响较大，而支点2 对一阶临界转速几乎无影响。因此，可通过优化支点1 支承刚度来匹配机台的一阶临界转速。

其次，基于粒子群算法进行支点1 刚度优化。以某机台实测数据为例，风扇转子振动响应随转速变化如图5所示，可知该机台的一阶临界转速N1为6 200 r/min 左右，按照经验值固定支点2 的支承刚度为1.0×108N/m，通过粒子群寻优算法得到支点1 的刚度。

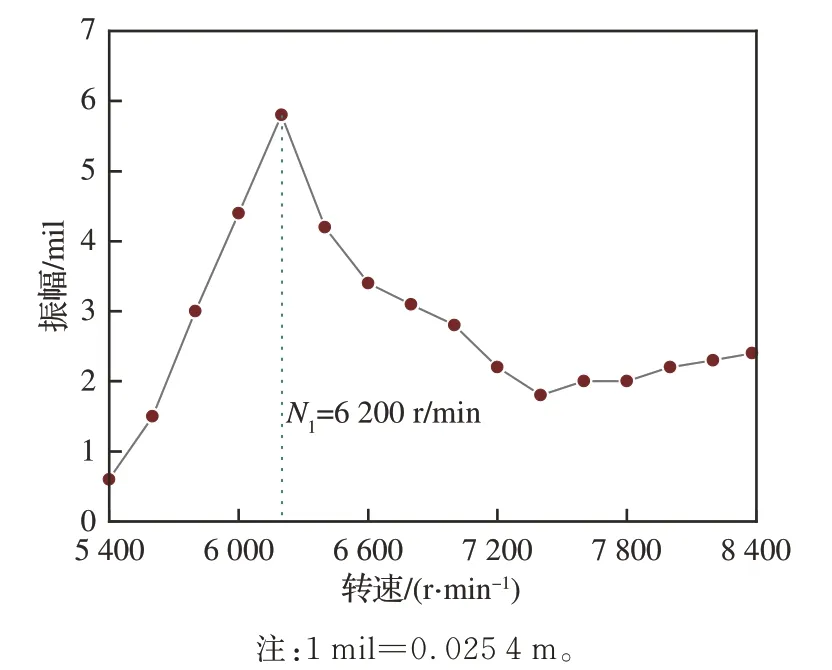
图5 实测某机台振幅随转速变化曲线Fig.5 Variation curve of amplitude with speed for machine

利用自主编写的基于Python 的可快速调用的动力学软件和风扇转子有限元模型迭代计算一阶临界转速。根据粒子群算法原理，设计临界转速为f(K)，将转子支点1 的支承刚度K作为粒子的位置，将实测与设计临界转速的差F(K)的绝对值作为粒子群的适应度函数：

计算流程和结果如图6 和图 7所示。由图 7可见，利用粒子群优化算法最终得出K1为2.3×107N/m，将其添加到有限元模型中进行计算得一阶临界转速为6 203 r/min，如图8所示，与实测临界转速误差仅为0.05%，表明有限元模型得到优化，且匹配实际机台特性。

图6 粒子群算法优化K1Fig.6 Particle swarm optimization K1

图7 支点1 刚度优化Fig.7 Stiffness optimization of fulcrum 1

图8 模型优化后临界转速Fig.8 Critical speed after model optimization

2.3 基于模型和动平衡数据反演特征参数

2.3.1 计算Kss和Ksd

基于风扇转子优化后的模型计算Kss和Ksd，流程如图9所示。

图9 Kss 和Ksd 计算流程Fig.9 Kss and Ksd calculation process

2.3.2 计算Kcs

在试验台架上采用锤击法可以测试Kcs，但对某机台进行动刚度Kcs测试时，发现前后2 次锤击测试的动刚度Kcs误差较大，如图10所示，会导致不平衡量计算错误。

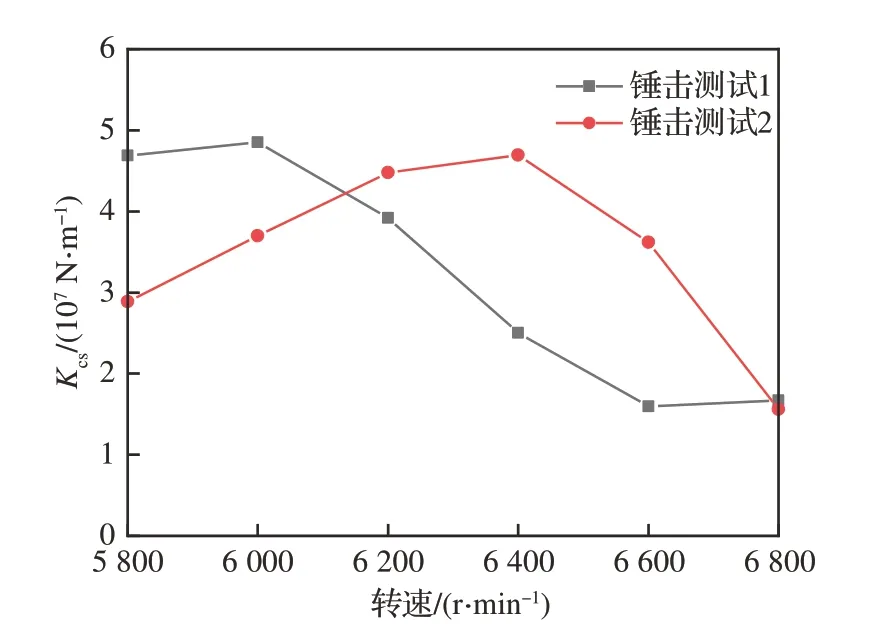
图10 锤击测试所得动刚度KcsFig.10 Dynamic stiffness Kcs from hammer test

当前，发动机机台具有大量动平衡数据，而动平衡数据中包含着转子动力学信息，未能有效利用。因此，本文提出一种基于动平衡数据反演参数Kcs的方法。由图1 的振动传递路径分析可知，机匣到动平衡平面的动刚度关系如图11所示。通过反演理论提取动平衡数据中的相关动力学信息，由于转子的不平衡力主要由不平衡量产生的离心力所致，因此可得到式（6），进而得到Kcd；结合式（4）即可得到Kcs，如式（7）所示。

图11 振动传递路径中的动刚度Fig.11 Dynamic stiffness in vibration transmission path

通过该方法可优化出不同转速下的Kcs，图12所示是同一机台通过2 种动平衡方法所得Kcs，对比锤击测试所得Kcs可知，经过2 种动平衡数据优化得到的动刚度较为接近，具有较高的精确度，证实了利用动平衡数据优化出的动刚度Kcs更加准确，可用于风扇转子本机平衡。

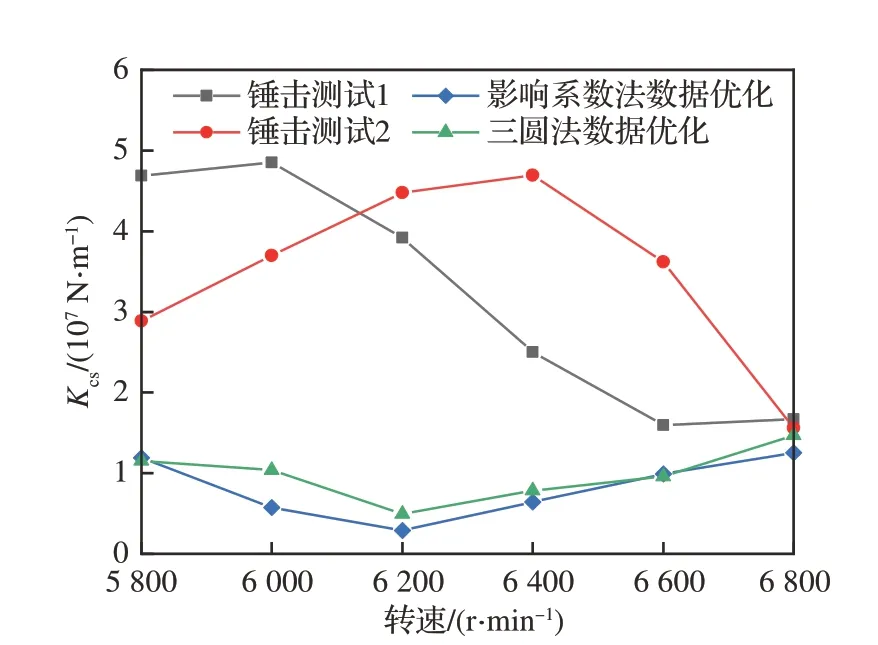
图12 不同方法计算的Kcs 参数Fig.12 Kcs parameters calculated by different methods

2.4 基于模型和特征参数反演不平衡量

确定风扇转子反演模型的特征参数后，由式（6）和式（7）可建立多转速下的转子不平衡量、模型特征参数和机匣响应之间的线性矩阵方程：

通过对式（8）进行广义求逆可得：

根据式（8）和式（9）只能求得不平衡量的大小，并不能确定不平衡量的位置。为此选择图1所示风扇转子前支点轴承内部改装后的分油盘作为试重平面，建立试重与原始不平衡量大小和位置的关系，如图13所示。图13 中，U0为转子原始不平衡量大小；U1为试重大小；U01为添加试重后合成不平衡量大小；α为试重角度；β为不平衡量的位置；γ为试重与不平衡量的夹角。U0和U01均可通过式（9）算出，则夹角γ为

图13 不平衡量位置识别Fig.13 Unbalance location identification

由于反余弦函数的对称特性，在[-π，π]范围内的同一函数值会对应2 个自变量，且两者互为相反数，因此可得到不平衡量的2 个位置为

根据式（10）和式（11）可以得出不平衡量的2 个位置，若再进行一次试重，则可以得到不平衡量的唯一位置。至此，基于真实数据反演的风扇转子本机平衡方法原理如图14所示。

图14 基于真实数据反演的风扇转子本机平衡方法Fig.14 Principle of fan rotor local balancing method based on real data inversion

3 本机平衡现场试验

3.1 建立机台特征参数库

不同机台发动机动力学特性差异较大，需分别建立各自的特征参数库。以具有接近临界转速（6 200 r/min 左右）的2 机台为例，基于2.1 节～2.3节的方法建立特征参数库，如表1和表2所示。

表1 机台1 动刚度KcsTable 1 Machine 1 dynamic stiffness Kcs

表2 机台2 的动刚度KcsTable 2 Machine 2 dynamic stiffness Kcs

以机台2 的转速为参考，机台1 内对应参考转速的Kcs通过插值法得出，对比2 机台的动刚度Kcs，如图15所示。由图15 可知，在临界转速6 200 r/min 前后，机匣测点至支点1 的动刚度Kcs呈先减小后增大的趋势；2机台的动刚度Kcs在一阶临界转速之前差异不大，临界转速之后差异增大。因此在对不同的机台进行动平衡时，需建立各自的反演模型参数库。

图15 机台1 和机台2 的动刚度对比Fig.15 Comparison of dynamic stiffness of machine 1 and machine 2

3.2 现场平衡结果分析

应用本方法对上述2 机台进行现场动平衡，均获得了较好的抑振效果，在全转速范围内实现了100%的振动抑制。其中机台1 降振达40%以上，机台2 降振达43%以上。现以机台2 为例阐述动平衡实施过程。首先，在试车台架上拆下发动机进气帽罩等相关组件，选择图1所示风扇转子前支点轴承内部改装过的分油盘作为试重平面，配平时再折算到配重平面。选择试重为1 123 g·mm∠-5°，实测机台2 的初始振动及试重后振动如表3所示。

表3 初始及试重振动幅值Table 3 Initial and trial recovery amplitude

根据式（9）～式（11）计算可得各转速下的不平衡量的大小及位置如表4所示。因现场实际记录缺少部分振动响应值，故未能计算出相应配重位置。

表4 不平衡量的大小及位置Table 4 Size and location of unbalance

用表4计算结果进行动平衡，从表中可以看出，6 600 r/min 之后的不平衡量均相差不大，但综合考虑到不平衡量与配重角度2方面因素，不难看出6 600 与7 600 r/min 2 个转速下配重位置最为接近，因此取两者平均值1 654.5 g·mm 作为配重大小；参考现场试重角度210°的抑振效果，选取配重角度237.5°（排除112.5°），即：1 654.5 g·mm ∠237.5°。由于受平衡螺钉重量及位置限制，最终实际添加的矫正不平衡量为1 600 g·mm∠235°，配平前后的振幅变化如图16所示。

图16 平衡前后振幅变化Fig.16 Amplitude changes before and after equilibrium

根据配重结果可知在转速范围内全部实现了降振，降振达43%～68%，如图17所示。

图17 振动降幅百分比Fig.17 Percentage of vibration decline

4 结 论

针对发动机风扇转子现场动平衡效率低，且大量动平衡数据未能有效利用的问题，本文提出一种基于模型和现场真实动平衡数据反演的风扇转子本机平衡方法。通过动平衡数据提取机台的动力学特征参数信息并建立机台的反演特征参数库，用于下一次动平衡计算。通过机台现场动平衡验证了该方法的有效性。

1） 风扇转子有限元模型的精确度是此动平衡方法的关键，所用模型的动力学特性必须与真实机台保持高度的一致。

2） 利用锤击法所测动刚度Kcs误差较大，通过机台的真实历史动平衡数据优化动刚度Kcs，可提高其精确度，可为风扇转子本机平衡提供较高匹配度的机台参数。

3） 本方法无需键相，最少试重1 次，至多试重2 次，减少了启停机次数，且对风扇转子能起到较好的抑振效果。

4） 风扇转子作为发动机低压转子的前端，降低风扇转子的振动对低压涡轮转子的振动也具有一定的改善。

本方法通过建立机台反演特征参数库，提高动平衡效率，与机台匹配度越高动平衡效果越好。因此需要大量已有机台的动平衡数据优化风扇转子的动刚度参数，这也造成本方法应用的局限性。