基于多指标动态优先级的无人机协同路径规划
王祝,张梦通,张振鹏,徐广通
1.华北电力大学(保定) 自动化系,保定 071003
2.浙江大学 湖州研究院,湖州 313002
近年来,无人机(Unmanned Aerial Vehicle,UAV)集群在物流配送、电力巡检等领域发挥着越来越重要的作用[1-2]。为保证多架无人机在复杂环境中高效协同完成任务,需要对无人机集群的路径进行科学合理的设计[3-4]。
多无人机协同路径规划需要在考虑协同约束的情况下,以最小代价合作完成任务为目标[5-7],为多架无人机生成安全可行的飞行路径。协同约束的处理是多无人机协同路径规划的关键,按照约束处理方式的不同,可分为耦合规划和解耦规划两类[8]。与耦合规划相比,解耦规划结果虽然不能保证路径最短,但具有显著的效率优势。
优先级规划作为解耦规划的主要方式[9-10],最早由Erdmann 和Lozano-Pérez[11]提出,是指在规划过程中优先级低的个体规避优先级高的个体,以实现集群个体之间避撞约束的解耦。目前,优先级解耦规划方法在自动导引运输车(Automated Guided Vehicle,AGV)领域已得到广泛研究[12-15]。文献[12]采取粒子群优化算法对多AGV 进行路径规划,提出基于时间优先级的粒子迭代更新机制,加快了求解收敛速度,但由于优先级固定,可能出现某个AGV 长时间等待导致系统效率变低。文献[13]提出一种基于动态优先级和改进蚁群算法的多AGV 路径规划算法,根据AGV 电池剩余电量分配优先级,提高了AGV 电力使用效率,但仿真环境简单,AGV规模小,当规模增加时,算法效率难以保证。文献[14]提出基于时间窗的优先路径规划算法,计算受影响AGV 与延迟AGV 之间的相对距离来更新优先级,解决了多辆AGV 的时延问题。但在无延迟情况下,采用动态窗口算法规划路径,该方法可能会得到局部极小值。文献[15]提出事件驱动的优先级更新逻辑,分为2 个优先级模块以应对AGV 单机或编队运动下的优先级更新,旨在保证编队运动及单机通过交叉路口时避免碰撞。其中,在计算通过交叉路口AGV 优先级时,赋予更接近公共路点AGV 更高的优先级,虽然该方法能解决当前冲突,但降低了结果最优性。
在多无人机协同路径规划方面,文献[16]提出了一种基于耦合度的优先级生成准则,利用无人机群潜在碰撞表示无人机间的耦合程度,提高了规划效率,但没考虑总路程等影响规划质量的因素,路径质量难以保证。文献[8]将滚动规划与优先级规划结合,将无人机群路径规划问题分解成单无人机短时域路径规划问题,增强了算法实时性,但优先级固定,存在优先级不合理导致集群整体规划效率变低的情况。文献[9]考虑飞行时间短、剩余飞行空间大的无人机成功规避其他无人机的概率更大,提出了一种飞行时间驱动的动态优先级解耦机制,提高了收敛速度,但该机制仅考虑了飞行时间对协同规划的影响,没有充分考虑其他指标,如航路长度、碰撞风险等,这些因素对多无人机协同路径规划的有效性和实用性也具有重要意义。因此,需要综合考虑多种因素,以制定更加全面、准确的优先级协同路径规划策略。
在优先级协同约束处理机制的基础上,单机路径规划算法也是影响协同路径规划效率的关键。针对个体路径规划,Daniel 等[17]将可视线引入A*算法,通过判断扩展节点与父节点之间是否存在可视线,实现了任意角度搜索的Theta*算法。但Theta*算法要对所有遍历过的节点进行视线检查,因此当栅格规模很大时,算法效率较低。为提高路径规划效率,Nash 等[18]对Theta*算法的搜索过程进一步改进,提出了Lazy Theta*算法。Faria 等分别提出基于稀疏网格[19]和基于单一网格[20]的Lazy Theta*算法,减少了存储空间和计算时间。但这2 种方法仅适用于稀疏环境的路径规划任务,对于密集环境下的路径规划存在不足。徐鹏飞等[21]针对机器人的运动学特性以及环境对路径规划结果的影响,提出了基于环境优化的Lazy Theta*算法,考虑环境中的动态障碍物,能够考虑环境的动态变化。但该算法计算复杂度高,需要较长的计算时间。此外,上述工作都是针对单机的路径规划研究,在多机路径规划方面如何减少基于Theta*的协同规划复杂度有待研究。
为了更好地权衡协同规划效率以及路径质量,本文的主要工作包括以下3 点。
1) 提出了一种基于多指标动态优先级的单边避碰机制,克服固定优先级存在的死锁问题;同时,考虑影响求解效率和路径质量的多个指标,构建动态优先级的生成模型,实现无人机优先级的合理分配。
2) 针对优先级协同框架下的单机路径规划,提出基于拥堵权值地图的Lazy Theta*算法,降低集群间冲突发生的可能性,提高求解速度。
3) 构建“路径重规划+起点等待”的局部冲突组合规避策略,可针对冲突情况选择合理的消解策略,以提高集群协同规划的求解速度。
1 问题描述
本节针对多无人机协同路径规划问题,完成任务指标和约束条件的构建。本文开展的无人机协同路径规划研究基于以下假设:
1) 无人机均以固定速度、高度飞行,因此只考虑二维平面的避障策略。
2) 无人机都能与中央控制器进行通信。
3) 处理局部冲突过程中,无人机存在一条能绕开其他无人机起点到达对应目标点的路径。
1.1 任务指标
通过多无人机的整体任务完成时间评判任务完成质量。
整体任务完成时间T为无人机集群中最大任务完成时间,反映了无人机系统的任务完成效率,可表示为
式中:Ti为第i个无人机的任务完成时间。
1.2 协同路径规划约束
1) 电量约束
要保证每架无人机都能完成任务,完成任务时第i架无人机的剩余电量记为pie,剩余电量pie满足:
式中:emin为保证无人机安全降落的最低电量。
2) 障碍规避约束
基于栅格化地图描述,可用一定数量的栅格区域来近似障碍。在无人机飞行过程中,为了保证其能规避环境中的障碍,无人机中心与障碍物边缘栅格中心之间距离D需满足:
式中:L为无人机轴距;R为栅格分辨率;s为飞行安全距离。
路径规划中将无人机作为质点,因此需根据无人机实际尺寸与飞行安全距离对障碍物边缘进行膨胀,以保证无人机不会与障碍发生碰撞。
3) 机间避撞约束
为确保无人机之间不会发生碰撞,需要考虑机间碰撞约束。因此无人机中心点之间的距离d需满足:
式中:c为机间安全距离。
2 协同路径规划算法
2.1 协同规划总体流程
协同路径规划分为单机路径规划层和多无人机系统协调层,单机路径规划层为每架无人机规划出与环境中障碍无碰撞的全局路径,再经过多无人机系统协调层完成无人机之间的协同运动。协同规划总体流程如图1所示。
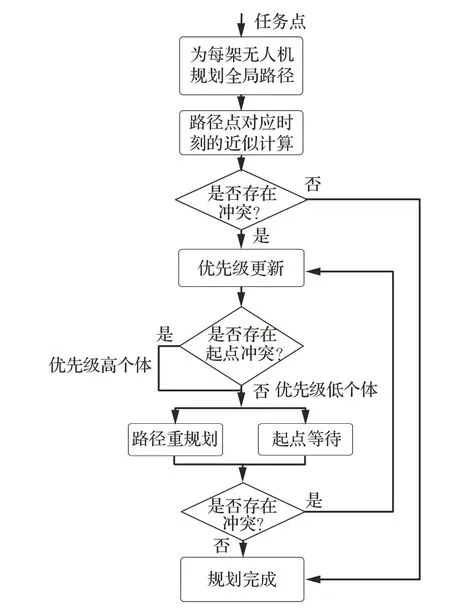
图1 协同路径规划总体流程图Fig.1 Flow chart of cooperative path planning
单机路径规划层的流程说明具体见2.4 节,下面主要对多无人机系统协调层的关键步骤进行说明。
1) 路径点对应时刻的近似计算
在解耦框架下,速度为v=[vxvy],时间步长为dt,第i架无人机在第k个时间步长的横纵坐标可由式(5)计算,并将第i架无人机的横纵坐标集合分别存放到飞行横纵坐标集合Φx={x1,x2,…,xn},Φy={y1,y2,…,yn}。
式中:β为上一时刻位置到当前位置的方向角。
2) 冲突判断和优先级更新
考虑机间协同约束,每架无人机根据上一步迭代过程中其他无人机在对应时刻的位置,来计算局部冲突。将冲突点位置以及发生冲突的无人机编号分别存放到Φpos和ΦUAV集合中。计算在同一点存在机间碰撞的无人机的优先级,完成更新。
3) 冲突消解
在优先级引导的单边避碰机制下,首先系统会先解决起点冲突,然后根据预设的避障策略选择规则,令优先级低的无人机采取相应避障策略。一旦完成一轮冲突消解,系统会进行下一轮迭代,直至获得满足全部协同路径规划约束的飞行路径。
2.2 多指标动态优先级更新策略
在协同规划中,处理机间碰撞的方式直接影响到规划效率和结果。由于每架无人机只能获得他机上一次迭代的位置信息,在相互避碰机制下,若冲突双方均采取路径重规划的策略,可能会出现路径反复振荡。为解决这个问题,采用动态优先级引导的单边避碰机制,通过不断更新优先级顺序,使高优先级无人机具有更大的行驶权利,避免与低优先级无人机发生碰撞。此外,不同的优先级计算方法决定了局部冲突发生时的不同决策方案,对规划速度和质量有重要影响。
本文动态优先级的确定考虑多个指标,具体包括以下4 个。
1) 碰撞风险
使用冲突次数作为指标衡量无人机之间的碰撞风险。各无人机之间的冲突次数计算公式如式(6)所示:
式中:Ci(ΦUAV)为编号为i的无人机在冲突无人机集合ΦUAV中出现的次数即冲突次数;D(ΦUAV)为冲突无人机集合长度。遍历ΦUAV中每个元素,若等于i,冲突权值δ为1,Ci(ΦUAV)累加,直至遍历结束。
2) 总路程S
无人机飞行路径的累计距离。
3) 等待时间Tw
无人机为消解机间冲突执行等待策略所等待的时间步长。
4) 剩余路程比Sr
即发生冲突时的剩余路程Sc和总路程S的比值,其表达式为
优先级更新策略的确定分为如下2 个部分。
1) 当碰撞风险不同时,无人机的碰撞风险越大,优先级越低。
冲突次数越多代表对应无人机碰撞风险越大。此时令碰撞风险大的个体执行规避策略有更大概率规避更多无人机。因此具有较高碰撞风险的无人机被赋予较低的优先级。
2) 当碰撞风险相同时,考虑总路程S、等待时间Tw、剩余路程比Sr,构建综合多指标的优先级计算模型,如式(8)所示。其中,无人机的综合指标Pi越大,其优先级越高。
式中:α、β、γ为对应指标的影响权重;、和为归一化后的各指标取值。其计算公式分别如式(9)~式(11)所示:
为优化任务完成效率,将更高的飞行权利分配给符合以下条件的无人机:总路程长、等待时间长、剩余路程比大。总路程越长的无人机需要更长的时间来完成任务,但其调整空间较小,因此其优先级较高。同时,过多地让同一无人机执行等待策略会延长整体任务完成时间,降低系统执行效率,因此等待时间越长的无人机也具有较高的优先级。而剩余路程比大的无人机具有更多的剩余飞行距离,赋予其更高的飞行权利有助于降低整体的飞行时间。
各个指标的权重α、β、γ选用层次分析法(Analytic Hierarchy Process,AHP)来确定,具体做法如下所示。
1) 构建如图2所示的层次模型。
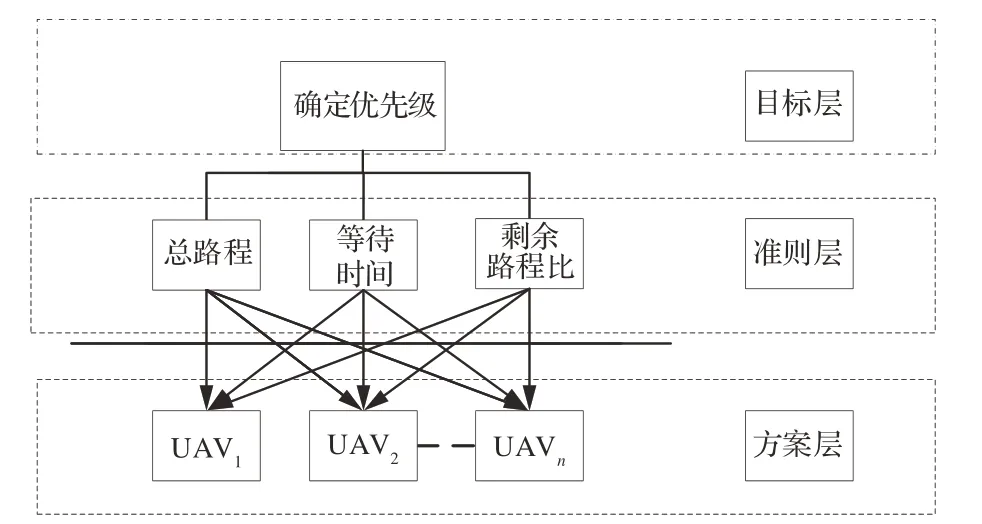
图2 层次模型Fig.2 Hierarchical model
2) 构造表1所示的比较判别对矩阵A。

表1 比较判别对矩阵Table 1 Pairwise comparison discriminant matrix
3) 权重计算
由各准则层对目标层权重aij根据式(12)计算特征向量的近似值Wi,再将特征向量标准化后得到式(13)所示的权重向量W。
4) 一致性检验
为了判断比较判别对矩阵是否存在逻辑性矛盾,需要通过式(14)进行一致性检验:
式中:λmax为最大特征根;N为比较判别对矩阵阶数;CI为一致性指标;平均随机一致性指标RI可根据对比矩阵的阶数给出[22]。当随机一致性比率CR<0.1 时认为计算所得的权重是正确且合理的。
2.3 冲突组合规避策略
针对局部机间碰撞规避,无人机一般采取路径重规划策略寻找规避冲突点的路径,受AGV采用等待策略消解机间冲突启发,等待策略可以避免大范围路径重规划从而降低计算复杂度。考虑到多旋翼无人机能够自主悬停,在安全点悬停等待一段时间同样能规避冲突。基于第1 节中的假设3)可知,各个无人机的起点均可以作为安全点,因此本文采取“路径重规划+起点等待”的组合策略规避机间冲突。
采用路径重规划的方式协调能力强,但规划耗时相对较长;采用起点等待的策略,由于无人机无需考虑避障,因此规划耗时短,而对于图3所示的冲突,起点等待策略下无人机飞行时间延长。因此需要结合2 种方式的特点,根据冲突情况建立策略选择公式,可表示为
式中:θ为冲突向量之间的夹角,当θ≥180°-ε时,执行路径重规划策略,否则执行起点等待策略;ε为容许值,可人为给定,以权衡协调能力及求解速度。
在局部碰撞检测中,需要将每架无人机ui(i=1,2,…,n)与其他无人机uj(j≠i)路径进行比较,即根据式(3)依次计算同一时刻Tk时ui的路径点pki和uj的路径点pkj之间的距离是否满足协同约束,将不满足协同约束的坐标集合Φpos记为:
冲突无人机集合可表示为
冲突向量之间的夹角θ,可表示为
当θ=180°时,表示冲突无人机对冲飞行,若执行起点等待策略,会出现路径更新后依然存在冲突的情况,起点等待策略效率变低,此时就应选择路径重规划策略。
另外,有一种特别情况需要指出,如图4所示的起点冲突,起点冲突定义为:假设UAVi的优先级大于UAVj的优先级,且UAVj的起点在UAVi的路径上。
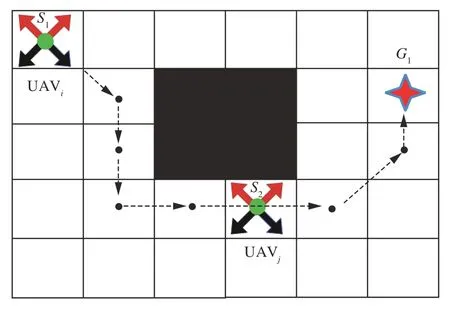
图4 起点冲突示意图Fig.4 Schematic diagram of start-point conflict
在多指标动态优先级的单边避碰机制下,由于高优先级个体会无视优先低个体,当发生起点冲突时,由于UAVi的优先级更高,UAVi无视UAVj,但s2并非是安全点,UAVj采取起点等待策略无法成功规避冲突。
因此,当发生起点冲突时,将优先级高个体加入待调整无人机集合,执行冲突规避策略。
利用组合策略规避冲突伪代码如算法1所示,具体流程如下所示。
步骤1(第1~3 行)确定规避策略
遍历冲突无人机集合,r_flag 为重规划标志位,当θ≥180°-ε时,r_flag 为True,即执行重规划策略。否则执行起点等待策略。
步骤2(第4~13 行)执行重规划策略

算法1 冲突规避伪代码Input:待调整无人机集合Φ͂adj、冲突无人机集合ΦUAV、冲突位置集合Φpos Output:飞行横纵坐标集合Φx、Φy 1.Φwait←∅ ∥记录执行过起点等待策略的无人机集合2.for i,uav in enumerate(ΦUAV):3.(r_flag,col_p)←select_strategy(Φpos)4. if r_flag:5. rpath_uav←Φ͂adj[i]6. k←uav.index(rpath_uav)7. Col_loc←Φpos[i][0][k] ∥待避开位置8. new_path←Exe_replan_strategy(rpath_uav,Col_loc) ∥重规划9. if not new_path: ∥无法重新路径规划10. if Φ͂adj[i] not inΦwait:11. (Φx,Φy)←Exe_wait_strategy(Φ͂adj[i])12. else:13. (Φx[Φ͂adj[i]],Φy[Φ͂adj[i]])←draw_pos(new_path)14. else:15. if Φ͂adj[i] not in Φwait:16. (Φx,Φy)←Exe_wait_strategy(Φ͂adj[i]) ∥起点等待17. if not col_detection()[0]:18. break 19.return Φx,Φy
令连续冲突点的第一个为待规避位置,将其视为障碍后进行路径规划,生成新路径new_path,若无法生成新路径,即new_path 为空,则执行起点等待策略规避冲突。
步骤3(第14~16 行)执行起点等待策略
为避免在同一轮迭代过程中某无人机重复执行起点等待策略,Φwait记录一轮迭代中执行过起点等待策略的无人机。判断当前无人机在本轮迭代是否执行过起点等待策略,若没有,在起点等待一个时间步长dt。
步骤4(第17~19 行)判断是否存在冲突
处理完本轮迭代中所有冲突后,判断系统是否还存在冲突,若系统中已无冲突,则跳出循环,否则继续下一轮迭代。
2.4 单机路径规划的改进Lazy Theta*算法
在协同规划总体流程中,每架无人机需要进行路径规划以达到任务点,Lazy Theta*算法[17]作为A*的改进算法,能实现任意角度的路径规划,消除了A*算法结果存在的“Z 字”抖动现象。
本文为了降低冲突发生的可能性,在Lazy Theta*算法基础上加入拥堵权值地图(记为Weighted Map Lazy Theta*,简称WM-Lazy Theta*),使无人机在单机规划层能避开“拥堵路段”,提高飞行效率。
WM-Lazy Theta*算法流程如图5所示,下面主要对本文改进所涉及的拥堵权值地图更新和节点代价计算进行说明。
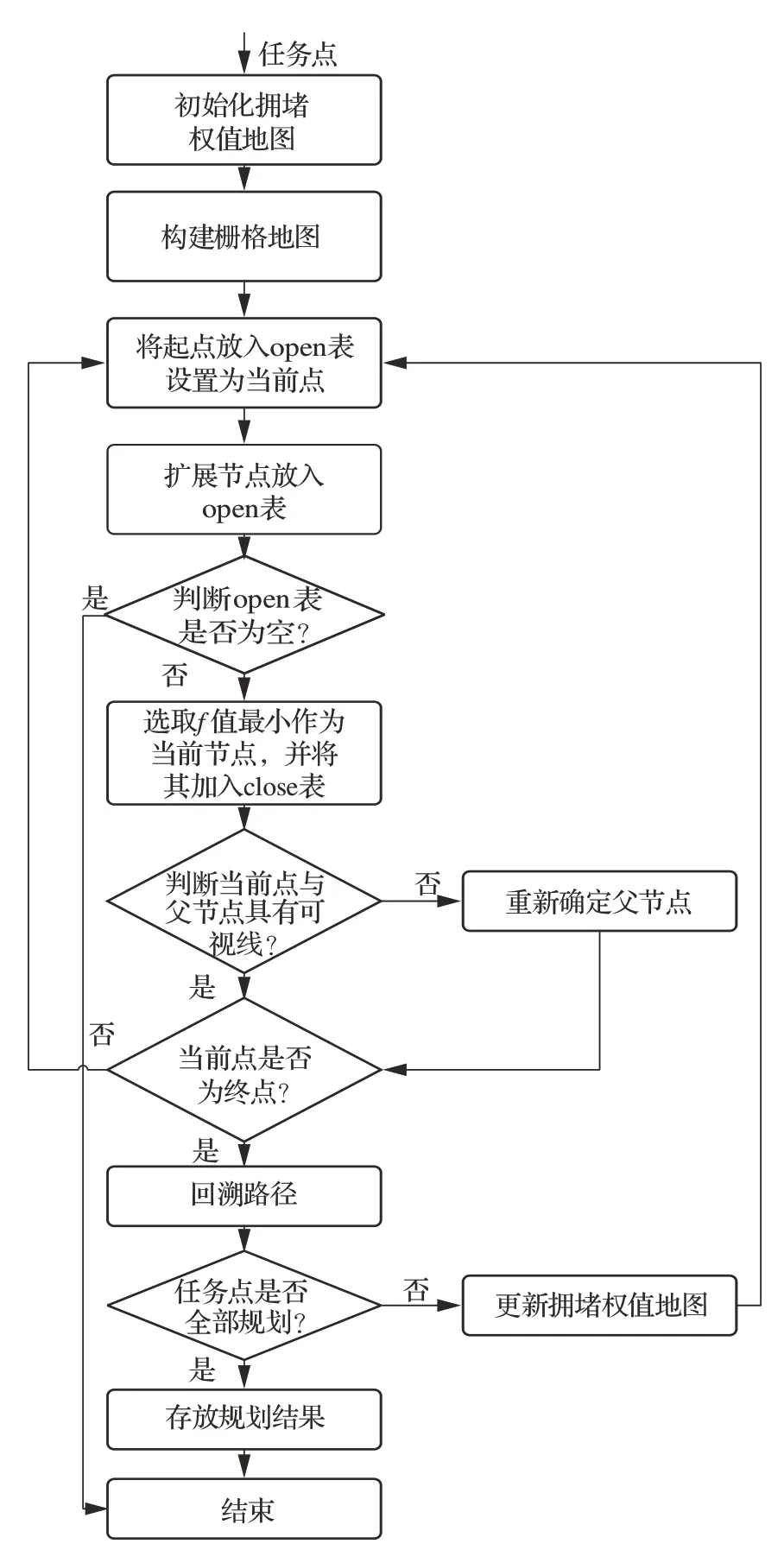
图5 WM-Lazy Theta*算法流程图Fig.5 Flowchart of WM-Lazy Theta*
1) 拥堵权值地图初始化和构建
将栅格地图划分为m个拥堵检测区域,构成拥堵权值地图。拥堵检测区域大小影响路径规划的效率及质量,若将每个栅格都作为拥堵检测区域,会增加路径规划复杂度;若合并过多的栅格构成大的拥堵检测区域,则会导致规划失去更优的路径结果。文中的拥堵检测区域划分方法如下。
步骤1确定最小拥堵检测区域
在构建栅格地图时,栅格分辨率与无人机轴距相同,即为L。每个栅格即为一个最小拥堵检测区域。
步骤2设置比例因子τ
拥堵检测区域面积为WH τ2,W和H分别为栅格地图的宽和高。
步骤3确定拥堵检测区域栅格数量
根据拥堵区域面积及栅格分辨率即可求得每个拥堵检测区域包含栅格数量为WH(τ2L2)。
步骤4为每个拥堵检测区域编号排序
从栅格地图左上角开始,按照从左到右、从上到下的顺序遍历所有的拥堵检测区域,分配从0 开始的连续整数作为编号。
每规划好一条路径后更新拥堵权值地图:记录该路径在每块区域的占有时间(进入和离开时间),并给定初始拥堵权值。若第i块区域(i=1,2,…,m)存在重复时间段,对应的拥堵权值进行叠加。
2) 节点代价计算
在扩展节点的过程中,计算到达当前节点的时间,查询当前节点所在区域的占有时间。若当前时间在占有时间内,则令M等于占有时间对应的拥堵权值,否则令M=0。节点价值的评估函数表示为
式中:f为节点的代价值;g为累计代价值,表示当前点到起点的路径长度;h为估计代价值,表示当前点到终点的路径长度;w为估计代价值的权重,w越大表示节点越倾向于“接近终点”。
图6 给出了一个权值地图的示例。想定为一个20×20 的栅格环境,每个栅格大小为1 m×1 m,比例因子设为10,因此将2×2 的栅格划分为一个拥堵检测区域,飞行速度为0.5 m/s,给定10 组起始点和终点,利用WM-Lazy Theta*按序号依次规划路径,图6 是规划完成后t=10 s 时的拥堵权值地图。若继续添加任务点进行路径规划,则在现有拥堵权值地图基础上进行节点代价计算。
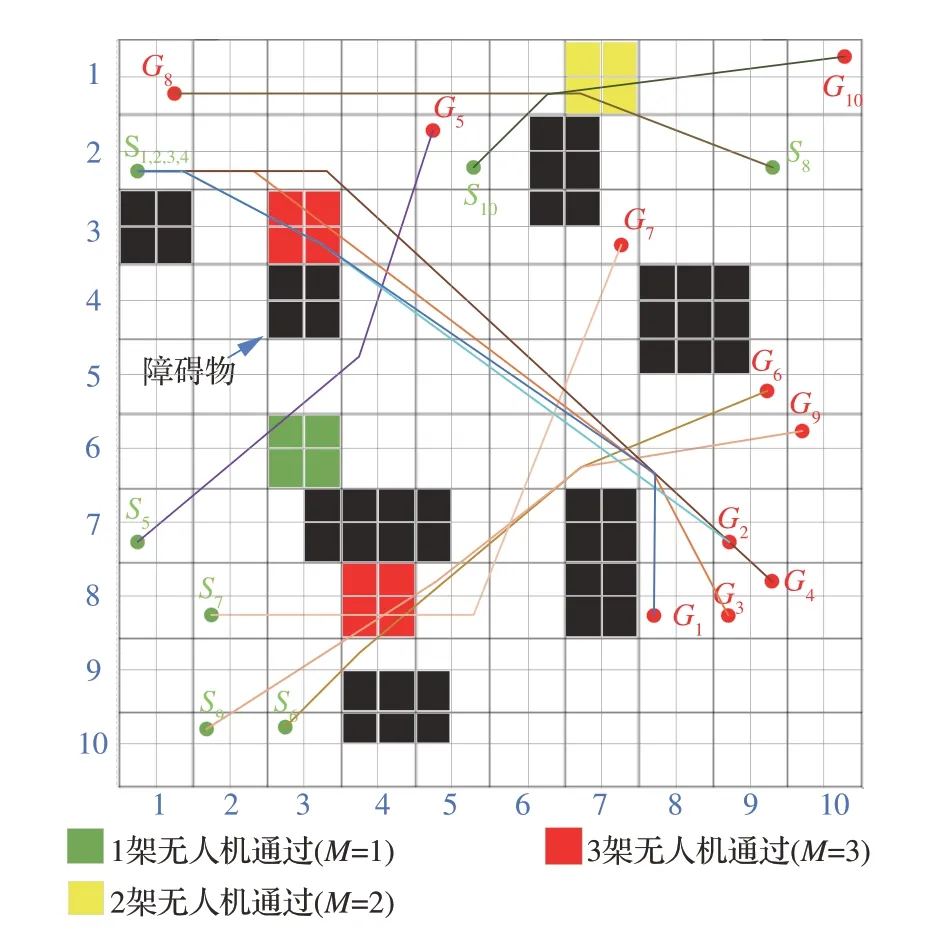
图6 t=10 s 时拥堵权值地图Fig.6 Congestion weighted map at t=10 s
图7 为引入拥堵权值地图后扩展节点示意图。当规划第4 条路径时,P点扩展的节点Pnext1、Pnext2占有时间分别为(9.4,12.2)s、(9,11)s,t=10 s 时对应区域内栅格的拥堵权值M=3,而在Pnext节点的占有时间(9,11)s 内所在区域没有被访问过,M记为0。分别对这3 个节点计算代价值得到fnext2>fnext1>fnext。因此Pnext为最优节点,达到避开拥堵区域的效果。
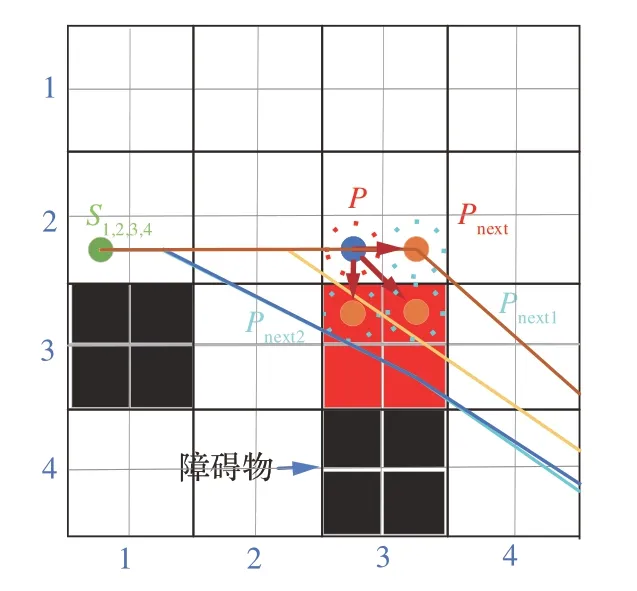
图7 引入拥堵权值地图后扩展节点Fig.7 Expanded nodes after introducing congestion weighted map
3 仿真试验与分析
为验证所提算法的可行性和优势,开展多无人机协同路径规划仿真对比试验。试验中,无人机飞行区域为20 m×12 m,设置栅格规模为50×30,使栅格分辨率与无人机轴距相同为0.4 m,每架无人机飞行速度均相同且恒定,设置为0.2 m/s。容许值ε=30°,最低安全电量emin设为5%,机间安全距离c设为0.1 m,飞行安全距离s设为0.1 m。
为模拟无人机运动过程中的电量损耗,采用下式表示t时刻的电量Et。
式中:stepw为等待步长;Es为无人机的起始电量。
3.1 协同路径规划算法有效性验证
分别选取无人机数量为5、10、15,开展协同路径规划算法有效性试验。拥堵权值地图设置中,比例因子设为10,即每个区域大小为5×3。
首先确定多指标动态优先级的指标权重。根据文献[23]所示的标度方法构造表2所示的比较矩阵,利用式(12)和式(13)求得各项指标权重。α=0.599 5,β=0.274 9,γ=0.122 9,再通过式(14)计算CR得CR=0.039<0.1,通过一致性检验,说明该权重合理。

表2 权重计算两两比较矩阵Table 2 Weight calculation pairwise comparison matrix
图8 给出了5、10、15 架无人机的协同路径规划结果图。图9 给出了3 种规模下最小距离变化曲线。针对障碍规避约束,根据仿真试验设定可得式(3)中()L+R2+s=0.5 m。由图9(a)可知,3 种规模下,无人机与障碍物之间的最小距离在任意时刻均大于0.5 m,因此,全局路径满足障碍规避约束。从图9(b)可知,3 种规模下机间最小距离均大于无人机轴距与机间安全距离之和0.5 m,满足协同约束。图10 展示了3 种集群规模下完成任务的剩余电量,由图10 可知,每个无人机的剩余电量均大于最低安全电量5%,即满足电量约束。
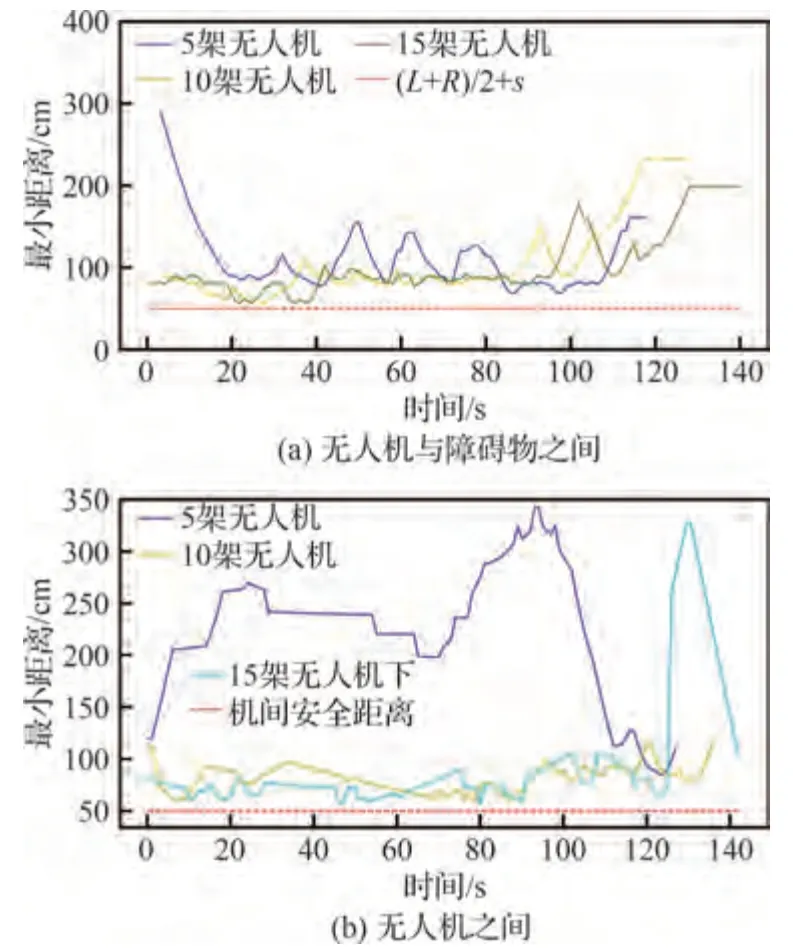
图9 3 种规模下最小距离变化曲线Fig.9 Minimum distance for three swarm-scale scenarios
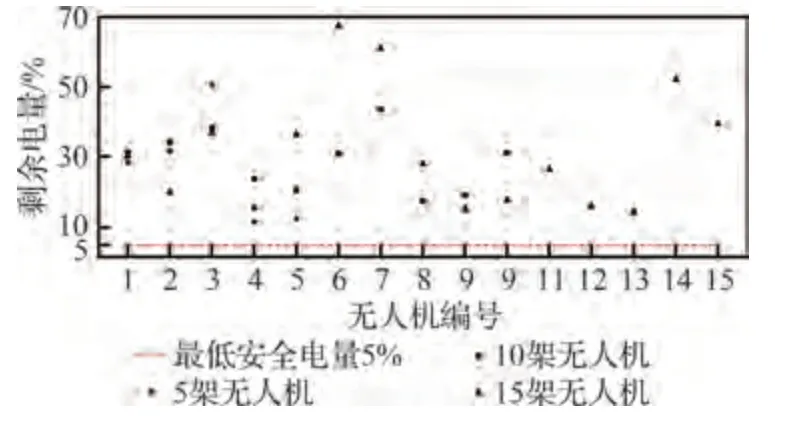
图10 3 种集群规模下完成任务的剩余电量Fig.10 Remained electricity for three swarm-scale scenarios
3.2 对比试验
本文提出的规划算法主要包含3 个改进部分:多指标动态优先级、WM-Lazy Theta*和组合规避策略,为验证每一部分的改进效果,分别开展优先级方法对比、单机路径规划方法对比和规避策略对比试验。
3.2.1 多指标动态优先级效果分析
为了分析本文提出的多指标动态优先级方法的求解效果,将其与飞行时间驱动的动态优先级方法[9]进行对比。
表3 为3 种无人机规模下,2 种优先级协同路径规划算法求得的的任务完成时间与规划耗时。由表3 可知,无人机规模为5 架时,多指标动态优先级相比飞行时间驱动的动态优先级虽然任务完成时间略有增加,但规划耗时减少85.0%,当规模增加至10、15 架时,多指标方法不仅任务完成时间较飞行时间驱动方法减少了8.23、3.8 s,规划耗时分别减少74.4%和47.8%。
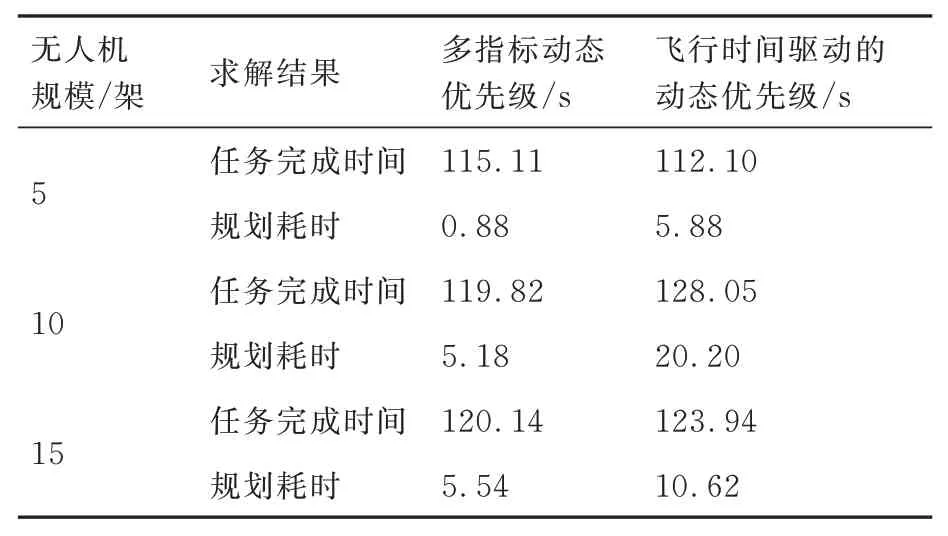
表3 不同优先级方法的求解结果对比Table 3 Comparison of results of two priority-based methods
表4 给出了5、10、15 架无人机协同规划过程中的优先级计算结果示例,来分析2 种优先级确定方法对规划结果的影响。表4 中{i,j}表示无人机i和无人机j存在冲突,且为无人机i优先级小于无人机j。图11~图13 分别给出了3 个示例下利用飞行时间驱动方法和多指标方法计算优先级过程中的指标值。
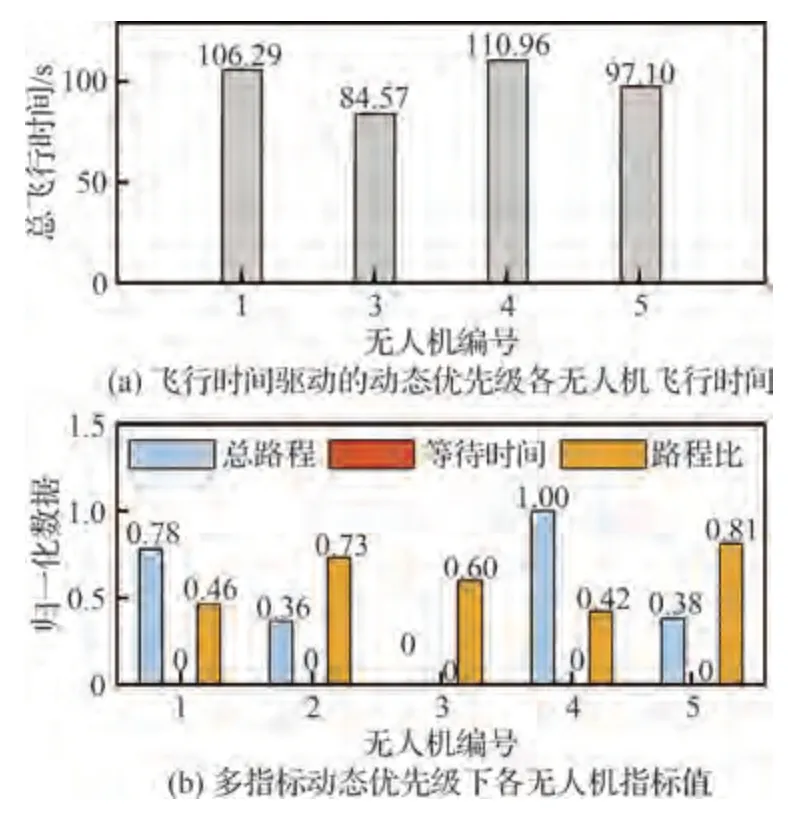
图11 5 架无人机第4 次迭代时的优先级指标值Fig.11 Priority index values at 4th iteration for 5 drones
由图11(a)可以看出,在5 架无人机协同规划的第4 次迭代中,对于飞行时间驱动的动态优先级方法,由于UAV3的总飞行时间最短,因此UAV3在与其他无人机发生冲突时,总是UAV3执行规避策略。在5 架协同规划的后续迭代过程中,也存在上述情况,使得UAV3的等待时间到达20 s,任务完成时间至104.57 s,但由表3 可知,该规模下整体任务完成时间为112.10 s,因此该规模下整体任务完成时间并没有受到影响。
而对于多指标动态优先级方法,发生冲突的无人机中,UAV5与其他2 架无人机存在冲突,其余均为与其他1 架无人机发生冲突,因此UAV5碰撞风险最大,优先级最低。其余4 架无人机的优先级由图11(b)中无人机各个指标的归一化值代入式(8)得出:P1=0.524 5,P2=0.305 7,P3=0.07,P4=0.65。设定的指标权重中,总路程与等待时间占主导地位且当前迭代步中各无人机的等待时间均为0 s,因此4 架无人机优先级的确定是由总路程确定。
由于整体任务完成时间并未受等待时间影响,此时2 种算法的主要区别在于对碰撞风险大的无人机的处理,多指标优先级优先令碰撞风险大的无人机做出规避,在任务时间上最优性受到限制,但缩短了规划耗时。
由图12(a)可知,在10 架无人机协同规划的第10 次迭代示例中,对于飞行时间驱动的动态优先级方法,UAV5的总飞行时间最短。当UAV5与其他无人机发生冲突,始终令UAV5执行避障策略,导致UAV5等待时间达到43 s,最终使整体任务时间延长至128.05 s。而对于多指标动态优先级方法,首先由冲突次数计算各无人机的碰撞风险:UAV8>UAV9=UAV1>UAV6。若碰撞风险不同优先级即可确定。优先级相同时,将图12(b)中各指标归一化值代入式(8)得到:P1=0.689 2、P6=0.786 6、P8=0.039 3、P9=0.845 5。多指标动态优先级考虑了等待时间,因此即使UAV1的总路程大于UAV9,由于UAV9等待时间过长,最终计算结果P9>P1。多指标动态优先级解决了某架无人机长时间等待的问题,于是多指标动态优先级的的整体任务完成时间及规划时间较飞行时间驱动的动态优先级都有所降低。

图12 10 架无人机第10 次迭代时的优先级指标值Fig.12 Priority index values at 10th iteration for 10 drones
当无人机数量增加至15 架时,飞行时间驱动的动态优先级会根据图13(a)中的总飞行时间计算优先级,持续令同一无人机做出规避策略的问题难以避免,进而发生某一无人机长时间等待的情况。多指标动态优先级在确定UAV11碰撞风险最大后,根据图13(b)所示的归一化数据计算各无人机优先级数值:P2=0.640 2、P9=0.937 1、P11=0.563 5、P14=0.061 5、P15=0.476 5,更加准确地量化了各无人机之间的协调性,因此多指标动态优先级在整体任务完成时间和规划耗时也均优于飞行时间驱动的动态优先级。
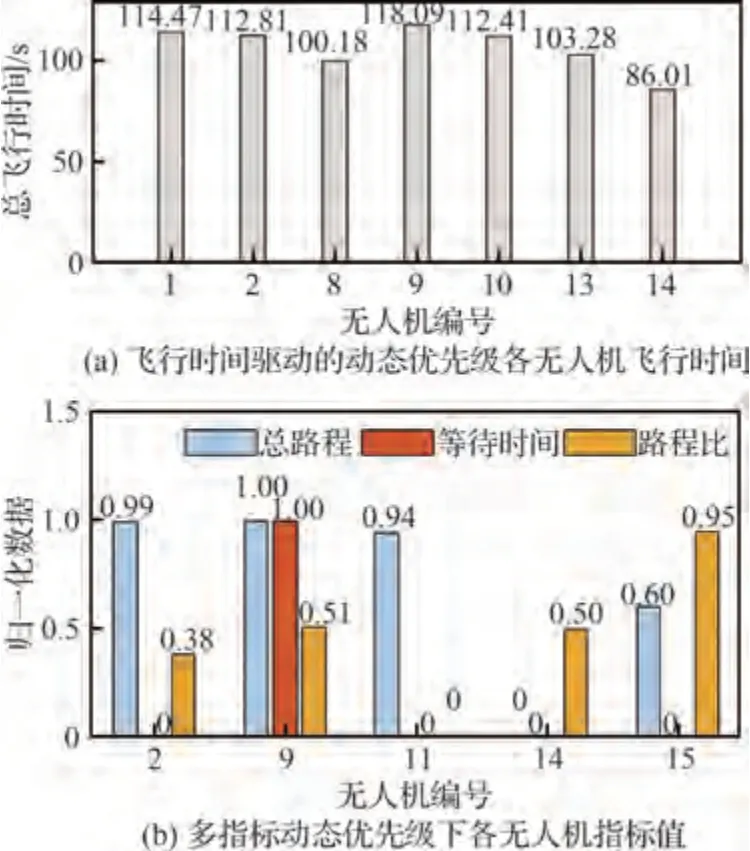
图13 15 架无人机第22 次迭代时的优先级指标值Fig.13 Priority index values at 22nd iteration for 15 drones
可见,多指标动态优先级方法相比飞行时间驱动的动态优先级方法,不仅可以提高多无人机系统的协调能力,还能够提高多无人机协同路径规划的计算效率。
3.2.2 WM-Lazy Theta*算法效果分析
为了评估WM-Lazy Theta*算法在协同规划中的性能表现,在不同无人机规模下,将其与Lazy Theta*进行对比试验。试验中,将栅格地图划分为100 块区域,在每个固定大小的拥堵检测区域内,有3 架及以上无人机在同一时间段经过则认定为“拥堵区域”。
表5 给出了在无人机规模分别为5 架、10 架、15 架时,2 种单机规划算法下的整体任务完成时间及规划耗时。由表5 可知,虽然在整体完成任务时间上会略有增加,但WM-Lazy Theta*方法的求解速度较Lazy Theta*方法分别提高了59.6%、67.3%、65.0%。对比表明WM-Lazy Theta*通过考虑不同区域的拥堵情况,能够更好地协调不同无人机之间的冲突,从而更快速地完成多机系统规划全局路径规划。
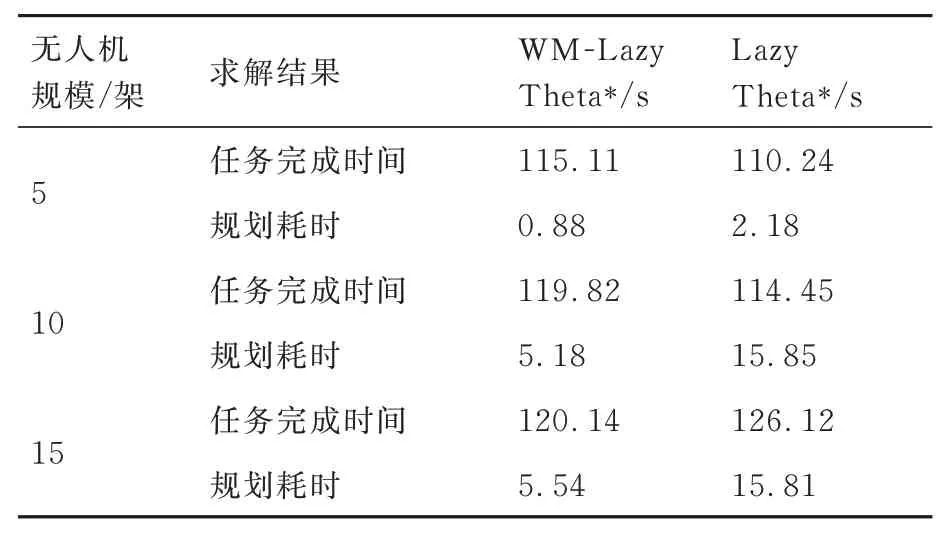
表5 不同单机规划算法的求解结果对比Table 5 Comparison of results of different UAV planning algorithms
图14 展示了15 架无人机协同时2 种算法所规划路径对应的拥堵区域结果。由图14 可知,WM-Lazy Theta*方法中“拥堵区域”相比Lazy Theta*大幅减少,且根据拥堵持续时间统计,改进算法对应“拥堵区域”的持续时间降低了72.1%。上述对比结果表明,WM-Lazy Theta*方法在规划时能够是使得无人机尽可能避开“拥堵路段”,拥有更快的协同规划求解速度。
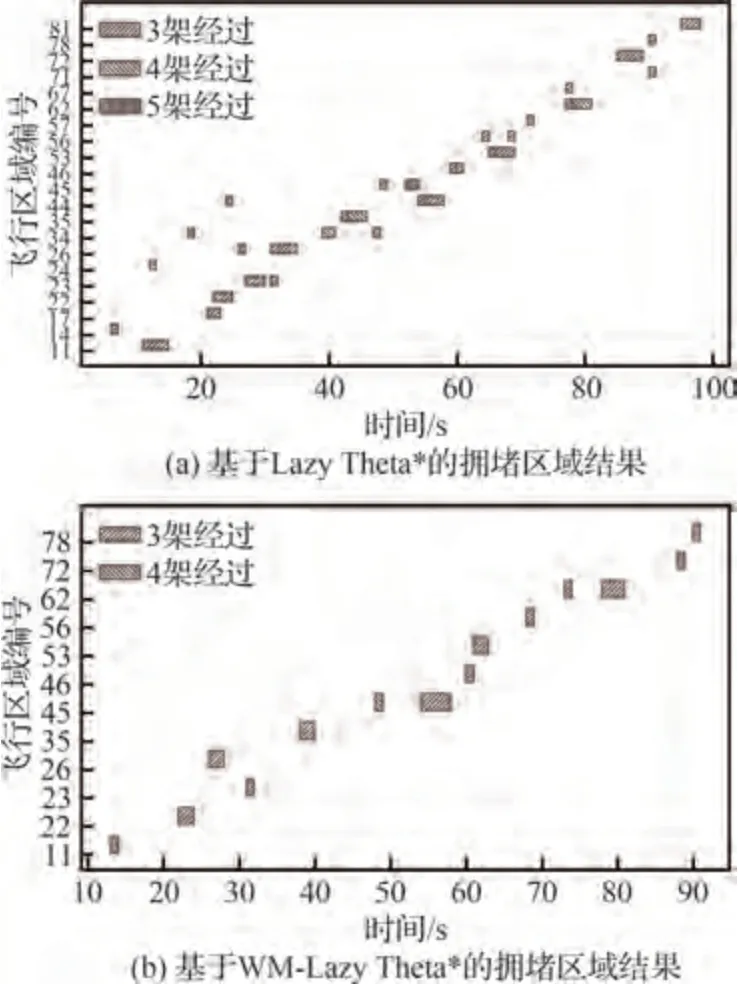
图14 15 架无人机的拥堵区域对比Fig.14 Comparison of congestion area for 15 UAVs
3.2.3 组合策略效果分析
为验证组合策略对规划的性能影响,在3 种无人机规模下,开展组合策略、重规划策略、起点等待策略对比试验。表6 为3 种规模下3 种算法的任务完成时间和规划耗时对比。通过表6 可知,仅有5 架无人机时,3 种策略下无人机整体任务完成时间几乎相同。然而,随着规模的增加,只执行等待策略的无人机的整体任务完成时间明显高于另外2 种策略。因此在整体任务完成时间方面,重规划策略最佳,而组合策略和起点等待策略的整体任务完成时间分别增加了2.81%、1.70%、1.60% 和4.70%、16.3%、28.5%。由于执行等待策略的时间复杂度更低,因此在规划耗时上,起点等待策略表现出最优的性能,较组合策略、重规划策略分别提高86.4%、85.5%、50.0%和90.5%、90.4%、70.3%。
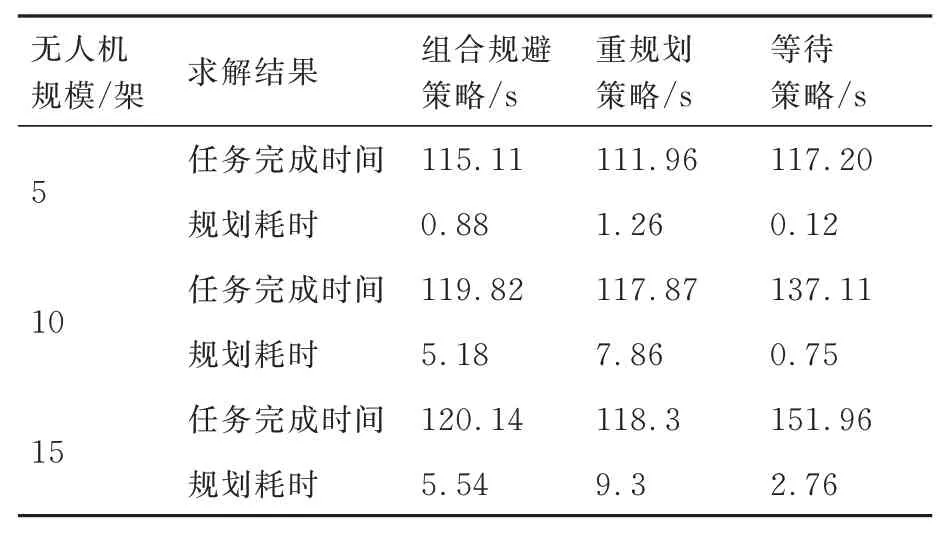
表6 3 种规避策略的求解结果对比Table 6 Comparison of results of three avoidance strategies
通过上述分析可知,安全点等待策略求解速度快,但协调能力差,重规划策略的协调能力好,但求解速度慢,而组合策略算法的协调能力与重规划策略相当的情况下,求解速度得到提高。在避障过程中,求解速度和协调能力存在一定矛盾关系。求解速度快但可能会在协调能力上牺牲一定的表现,而协调能力强可能导致求解速度较慢。因此,在选择避障策略时,需要综合考虑实际场景的需求,以确定具体采用哪种算法。如果在紧急情况下需要快速应对,那么起点等待策略可能是更好的选择;而如果需要较高的协调能力,那么重规划策略算法可能更为合适。在一些需要求解速度和协调能力平衡的场景下,组合策略算法则可能成为一个更好的选择。
4 结 论
本文针对多无人机协同路径规划提出了一种基于优先级的解耦规划方法,主要包括:① 发展了基于多指标动态优先级的单边避碰机制,并构建了动态优先级生成模型,实现了无人机优先级的合理分配;② 提出了基于拥堵权值地图的Lazy Theta*算法,降低全局路径中发生集群间冲突的概率,提高求解速度;③ 构建了“路径重规划+起点等待”的局部冲突组合规避策略,在保证协调能力的同时,提高了求解速度。最后通过对比试验验证了在不同无人机规模下,多指标动态优先级与WM-Lazy Theta*均提高了规划质量及求解速度,组合规避策略在保证协调能力与路径重规划策略相当的情况下,实现了求解速度提升,证明了本文提出方法的有效性。

