基于轨道可达域的机动航天器接近威胁规避方法

张赛，杨震，*，杜向南，罗亚中

1.国防科技大学 空天科学学院，长沙 410073

2.空天任务智能规划与仿真湖南省重点实验室，长沙 410073

3.上海机电工程研究所，上海 201109

随着技术的进步，在轨航天器数量急剧增加，并且具有了更加强大的机动能力。一方面，轨道机动使得轨道拦截、交会、飞越等空间任务成为可能；另一方面，在轨航天器面临被非合作目标机动接近甚至打击的风险。已有的不确定性事件［1］和X-37B、MEV 等空间实验［2-3］都表明太空安全形式已经变得非常复杂，因此开展来袭航天器威胁评估与规避方法的研究十分必要。

考虑实际工程约束，为了评估空间任务的可行性和安全性，有必要研究机动能力有限的非合作目标轨道机动可达域计算方法。航天器轨道机动可达域（Reachable Domain， RD）是在给定轨道机动约束条件下航天器所有可能到达位置的集合［4］，是机动航天器进行态势分析的有效工具。Caruso 等［5］首先将可达域的概念应用于弹道武器的可达性分析，Vinh 等［6］和Battin［7］随后将此概念扩展到弹道武器的拦截问题和具有固定速度的航天器轨道转移问题。在此基础上，Xue 等［8］研究了具有固定脉冲幅值的航天器单脉冲机动（三维）可达域，但求解精度有待提高。Wen 等［9］提出的将可达域包络求解问题转化为可达方向上矢径极值求解问题的方法，能够精确求解机动位置固定的单脉冲机动可达域。该方法被杜向南和杨震［10］所采用并作了进一步优化，求解流程更加简单。可达域方法已经在航天器地面轨迹覆盖区域分析［11］、目标飞越［12-13］、航天器轨道安全性分析与碰撞预警［14-15］以及轨道博弈［16-17］等空间任务的分析中得到应用。在轨道安全性分析中，可达域能够直观描述航天器轨道在非合作目标可达域范围内的危险区段，并得到航天器穿过危险区段时间［15］，即得到目标的威胁告警信息。

基于可达域获得来袭目标的潜在威胁告警信息后，航天器可以进行变轨以规避目标威胁。已有的航天器威胁规避方法主要分为针对无机动目标的碰撞规避策略和针对来袭机动目标的主动规避策略2 类［18］。对于无机动空间目标的碰撞规避，现有研究以碰撞概率计算为基础［19-20］，研究最优机动的计算方法和实施策略等问题［21］。相比于无机动空间目标，可机动空间目标产生的打击威胁对航天器来说更加危险且难以预测。目前对于航天器机动规避策略的研究较为充分［22-25］。在轨航天器对来袭机动航天器进行机动规避时，两航天器均主动施加控制但追求相反的相对位置状态，因此该过程属于轨道博弈的范畴［26］。部分学者研究了追逃博弈双边规划问题［27-30］，分别给出了博弈双方的追逃策略，上述文献研究对于航天器威胁规避策略的形成具有一定的参考价值。然而在空间攻防中，攻击方大多具备较高机动能力，地面站难以及时更新其异常机动信息，使得在轨航天器不能及时探测到被打击的威胁。因此如何通过有限信息分析来袭目标潜在威胁能力并设计主动规避机动策略对潜在威胁域进行避让具有一定的研究意义。

本文在现有研究基础上，提出了基于轨道可达域的机动航天器接近威胁计算、评估和规避方法。首先给出了航天器单脉冲轨道机动可达域的一般求解方法；其次，通过判断在轨航天器轨道在来袭航天器可达域内的区段得到危险区域，并基于两航天器进出危险区的时间定义危险区比例和时间窗口匹配性威胁评价指标；最后，给出了基于最小化危险区的航天器多脉冲机动主动规避策略，并通过仿真验证了所提基于轨道可达域的机动航天器接近威胁规避方法的有效性。

1 单脉冲轨道机动可达域求解

1.1 坐标系定义及轨道状态描述

1.1.1 坐标系定义

如图1所示，定义J2000 地心惯性坐标系SJ(OJxJyJzJ)：坐标原点OJ在地球中心；xJ轴沿地球赤道面和黄道面的交线，指向春分点ϒ；zJ轴和地球自转轴重合并指向北极；yJ轴根据右手法则得到。定义近心点坐标系Sp(Opxpyp)zp：原点Op位于地心；xp轴指向初始轨道近地点；zp轴指向初始轨道角动量方向；yp轴位于初始轨道平面内，并与xp、zp轴构成右手直角坐标系。

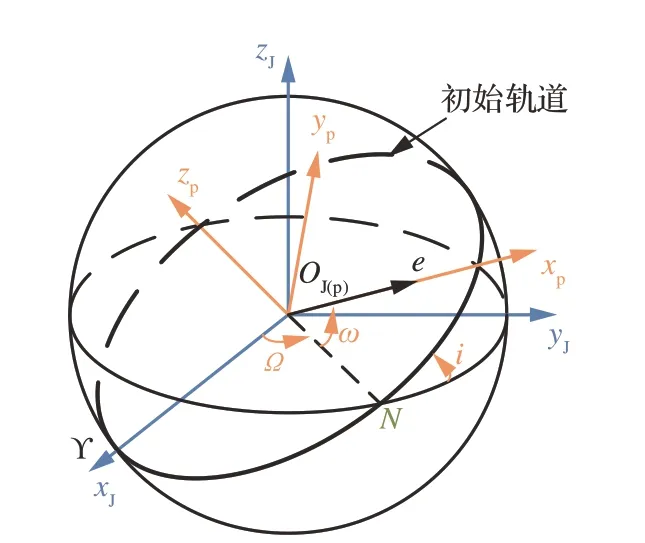
图1 坐标系位置关系示意图Fig.1 Illustration of defined coordinates

如图2所示，定义航天器LVLH 坐标系：原点O位于航天器质心；x轴与r重合；z轴指向轨道角动量方向；y轴位于轨道平面内，并与x、z轴构成右手直角坐标系。初始轨道上的LVLH 坐标系记为S0(O0x0y0z0)，转移轨道上的LVLH 坐标系记为S1(O1x1y1z1)。

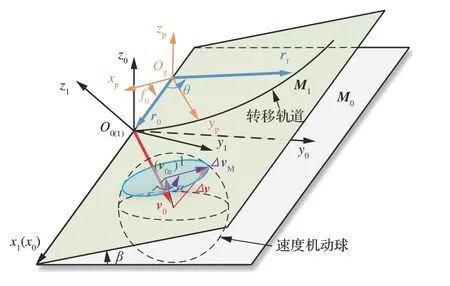
图2 坐标系关系与速度机动球示意图Fig.2 Illustration of defined coordinates and impulsive maneuvering ball

1.1.2 轨道状态描述

如图2所示，将航天器初始位置矢量和终端位置矢量分别记为r0和rf；定义航天器初始轨道平面为M0；转移轨道平面为M1；记M0和M1的夹角为β，r0和rf的夹角为θ。

设航天器在初始轨道上机动位置处的轨道根数为[a0e0i0Ω0ω0f0]，则r0在坐标系Sp下可表示为

初始速度v0在坐标系S0中可表示为

式中：μ=3.986×1014m3s2为地球引力常数；为轨道半通径。

初始速度v0在坐标系S1中可表示为［4］

将航天器的最大机动能力记为Δvmax，机动方向任意，因此其机动速度增量可以用速度机动球建模表示。 若航天器的机动速度增量为，其在转移轨道面内的投影为ΔvM，其大小为［4］

1.2 单脉冲轨道机动可达域求解方法

1.2.1 可达域问题描述

航天器单脉冲轨道机动可达域是围绕初始轨道的有限三维区域，该区域被一个边界面所覆盖，称为可达域包络［15］。通常情况下，二维平面上的包络由内包络和外包络构成，可达域及其包络的几何关系如图3所示，求解可达域的核心工作是确定空间中全部可达区域的包络。

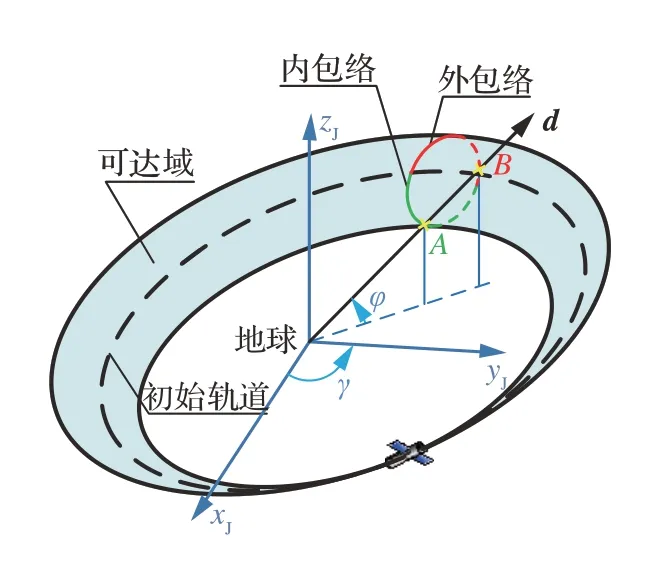
图3 初始轨道、可达域及其包络的几何关系Fig.3 Geometry of initial orbit， RD， and envelope of RD

为简化计算，可以将连续包络的求解离散为若干包络点的求解。在任意一个以地心为坐标原点的笛卡尔坐标系中，方位角γ和φ能够确定空间中的一个方向d(γ，φ)。若d(γ，φ)可达，可求得该可达方向上最近距离dmin和最远距离dmax，因此A(γ，φ，dmin)、B(γ，φ，dmax)两点分别为P上内包络和外包络的点。通过遍历参数γ、φ的取值能够得到所有包络点，最终得到可达域。

1.2.2 轨道机动可达性判据

将图3 中的坐标系选作近心点坐标系Sp，为使得Sp中的方向d(γp，φp)可达，需保证机动后的速度矢端能够落在边界速度双曲线（Terminal Velocity Hyperbola， TVH）上。此时，可达的判定条件为［4］

1.2.3 可达域求解算法

已知坐标系Sp中的一个可达方位d(γp，φp)，rf为该方位上任意终端矢径。航天器从r0以速度机动至rf，则基于二体轨道动力学模型可算得rf的大小为［10］

定义表达式［10］：

由文献［10］可知，对于机动位置固定的可达域求解问题，rf的方位角[γp，φp]确定后，rf矢径表达式（7）是关于变量α的一元函数，的零点可以通过求解P(α)=0 得到。

易知P(α) 至多存在2 个零点，记为和，同时将区间两端边界值设为和2π。将和分别代入式（7），得到、和。记4 个值中较大的为dmax，较小的为dmin，可得Sp坐标系下rf方向上的极值点位置坐标为

综上所述，可达域计算步骤为：

步骤1首先给出γp和φp用于确定空间中的一个方位。

步骤2根据式（6）判断该方位是否可达，若可达进入步骤3；若不可达，返回步骤1。

步骤3通过求解式（8）的零点求得该可达方位矢径极值，确定极值点坐标，即式（9），即可得到该方位上可达域包络。

步骤4重复步骤1～步骤3，通过遍历γp和φp的取值得到所有可达方位上的内外包络点，进而获得Sp中的近似包络，求得可达域。

2 在轨航天器轨道危险区求解及威胁评估

来袭航天器轨道可达域将会是围绕其初始轨道平面形成的扁平形区域。如图4所示，将来袭航天器轨道可达域与在轨航天器轨道的交集部分定义为在轨航天器轨道危险区。危险区会出现在来袭航天器初始轨道平面与在轨航天器轨道平面的交点附近，在危险区内，在轨航天器存在被接近的风险。

图4 在轨航天器轨道危险区示意图Fig.4 Diagram of danger area for on-orbit spacecraft

2.1 轨道危险区域求解方法

由于来袭航天器机动能力有限，因此要进行威胁规避机动策略设计，首先要判断危险区的存在性。

设来袭航天器机动前的初始轨道根数为[acecicΩcωcfc]；在轨航天器轨道的初始轨道根数为[atetitΩtωtft]。如图5所示，绿色轨道面为来袭航天器初始轨道，天球面交点纬度幅角为uc；蓝色轨道面为目标轨道，天球面纬度幅角为ut。

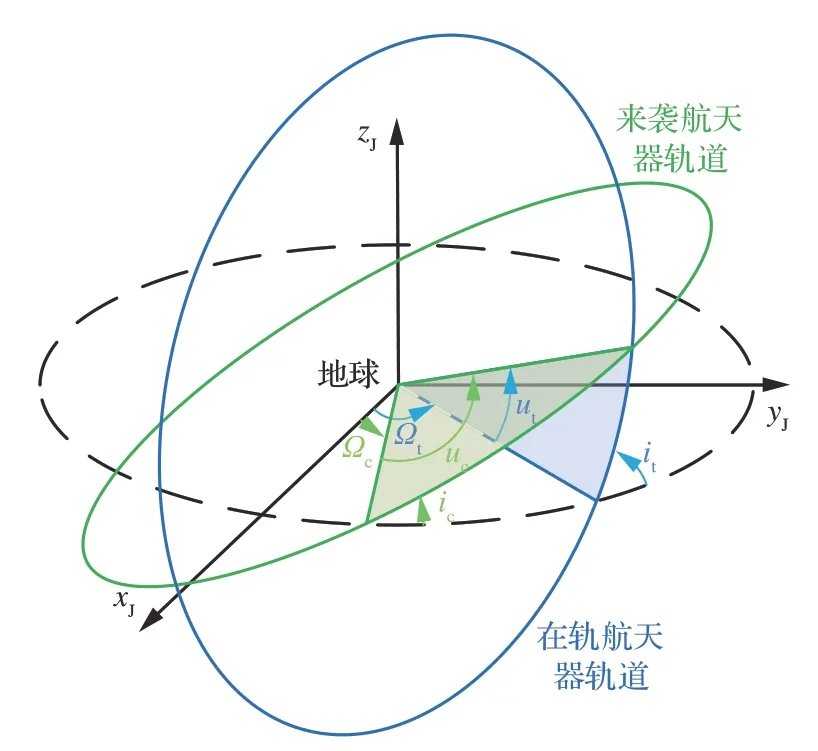
图5 轨道面天球交点Fig.5 Orbital celestial sphere node

在惯性坐标系SJ下，两轨道天球面的交点在惯性系中存在等式：

式中：rs表示天球的半径；M1(·)表示绕OJxJ轴旋转的转移矩阵；M3(·)表示绕OJzJ轴旋转的转移矩阵。

进一步可以求得

从式（11）中可以求解得到uc和ut的值，且由图5 可知，uc和ut有2 组解关于引力中心对称，且是一一对应的，即

uc1和ut1对应的交点在来袭航天器初始轨道及在轨航天器轨道上的真近点角fc1、ft1表示为

若来袭航天器在fc1处采取轨道机动，则两航天器轨道在天球面的交点的方向在来袭航天器近心点坐标系中可表示为

若来袭航天器轨道可达域与在轨航天器轨道存在交点，如图6所示，虚线表示轨道面交线，绿色轨迹表示目标轨道，在右侧在轨航天器轨道存在危险点如图中红点所示。

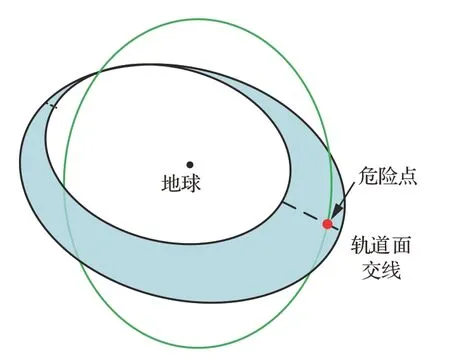
图6 在轨航天器轨道危险点Fig.6 Danger point of on-orbit spacecraft

由于来袭航天器机动可达域具备一定厚度，因此在轨航天器轨道穿过该威胁域的危险区段应是图6所示危险点附近一段延伸的轨道区段。

二体假设下航天器任意时刻的位置速度可通过初始时刻t0=0 时的位置速度r0、v0外推得到。设外推时间步长为Δt，ti时刻表示为

通过二体轨道外推确定的ti时刻在轨航天器位置ri［7］在基于来袭航天器初始轨道建立的近心点坐标系Sp中可以表示为

进一步，在来袭航天器近心点坐标系中确定(ri)p的空间指向[γi，φi]为

将式（17）所得ti时刻在轨航天器的空间指向[γi，φi]代入1.2.3 节中可获得来袭航天器在该指向上的可达范围[ri，min，ri，max]，此时在轨航天器的地心距为，分析目标地心距与来袭航天器可达域之间的关系可能有如下2 种情况：

按照式（15）给定的时间步长对目标轨道外推并记录所有处于危险区的时间范围[tmin，tmax]，如图7所示。

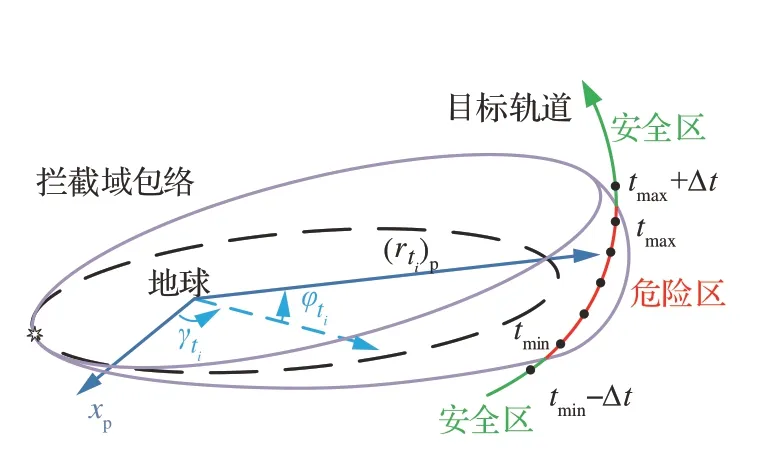
图7 在轨航天器轨道危险区的时间范围Fig.7 Time window of on-orbit spacecraft’s danger area

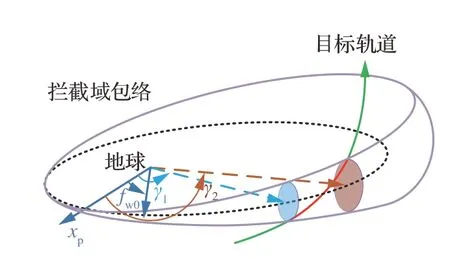
图8 来袭航天器与危险区关系Fig.8 Relationship between incoming maneuvering spacecraft and danger area

由于在轨航天器轨道是否处于危险区是按照步长Δt外推进行遍历搜索的，因此图7所示危险区的2 个端点应分别在[tmin-Δt，tmin] 和[tmax，tmax+Δt]时间内获得。危险区端点时刻的精确区间可以通过二分法求得。 以[tmin-Δt，tmin]区间内的端点为例，具体步骤为：

步骤1根据式（16）确定t=(tmin+tmin-Δt)2 处目标轨道地心距(ri)p∈[ri，min，ri，max]。

步骤2若区间长度ε＞ε0（一般可取为0.001s），则进入步骤3；否则结束计算，所得区间窗口记为危险区时间窗口。

步骤3判断该地心距是否位于危险区内，若是，则用t替换tmin，组成新的时间范围；若不是，则用t替换tmin-Δt，组成新的时间范围；重复步骤1 和步骤2。

对危险区的2 个端点时刻分别执行上述步骤从而得到满足高精度要求的危险区时间窗口[t'min，t'max]。

2.2 威胁评价指标

当在轨航天器的轨道存在危险区时，其受威胁程度取决于两航天器轨道关系及来袭航天器的机动能力。下面给出指标描述在轨航天器受来袭航天器的威胁程度。

2.2.1 基于危险区比例的评价指标

由图 7 可知，可采用危险区时间占轨道周期的比例作为评价指标。设2.1 节所述方法判定危险区存在，且经过二分法求得在轨航天器处于危险区的时间范围为[t'min，t'max]，则危险系数ξD表示为

式中：危险系数ξD越大，在轨航天器轨道位于威胁可达域内的比例越高，被来袭航天器打击的可能性就越大。

2.2.2 考虑时间窗口匹配性的评价指标

除了考虑上述危险系数ξD外，还需要考虑来袭航天器到达危险区时间和在轨航天器本身到达危险区时间窗口的匹配性。下面给出来袭航天器到达危险区的时间窗口估计方法。

图 8所示蓝色平面为危险区的2 个端点垂直于来袭航天器初始轨道平面在威胁域内形成的2 个截面。2 个截面在基于来袭航天器初始轨道建立的近心点坐标系Sp中，所对应的方位角γ分别为γ1、γ2。危险区2 个端点的位置分别为rtmin、rtmax。当来袭航天器进行机动后，转移轨道的平均角速度可以表示为

式中：atran为转移轨道的半长轴。

由于来袭航天器采取的脉冲机动限制在速度机动球内，其到达危险区的时间窗口可以根据轨道转移时间取值范围进行估计。由式（19）可知，在转移相位相同的情况下，转移时间仅与转移轨道的半长轴atran相关。又由于当来袭航天器的最大机动能力Δvmax全部用于进行面内机动时，可以使atran的变化幅度最大，因此本文采用来袭航天器进行轨道面内机动到达γ1、γ2截面的时间极值作为到达危险区时间窗口的保守估计。由于γ1截面距离出发点更近，对应时间窗口估计的下界；γ2截面距离出发点更远，对应时间窗口估计的上界。

设来袭航天器在fw0处脉冲机动大小为Δvmax，方向与原速度方向相反，则由式（2）可知，机动后速度为

由rw1和vw1可算得机动后转移轨道的半长轴aw1，偏心率ew1以及机动位置真近角fw1，则截面γ1处对应的真近角可以表示为

由真近角与偏近点角转换关系，能够得到来袭机动平台在机动位置和到达γ1截面处对应的偏近点角Ew1、Eγ1。进而可得按照最大轨道平均角速度到达危险区的最小时间为

同理为了得到来袭航天器到达危险区的时间窗口上界，在fw0处施加脉冲大小Δvmax，方向与原速度方向相同。

与求解窗口下界方法类似，可以求得来袭机动平台在机动位置和到达截面γ2处的偏近角Ew2、Eγ2，则按照最小轨道平均角速度到达危险区的最大时间为

式（22）和式（24）确定的来袭航天器到达危险区的时间窗口比来袭航天器实际到达危险区具体危险点的时间范围更广，可以用于判断来袭航天器与在轨航天器时间窗口的匹配性，从而评价危险区有效性。

至此能够得到在轨航天器处于危险区的时间范围[t'min，t'max]和来袭航天器到达危险区的时间窗口[tw，min，tw，max]。记tp为2 个时间窗口的交集大小，定义危险系数ξT描述来袭机动平台与在轨航天器的时间窗口匹配性

3 接近威胁规避策略

接近威胁规避策略即在轨航天器的脉冲机动方案，其目的是实现对来袭航天器的威胁规避。本文通过优化方法求解满足约束条件的燃料最省威胁规避策略，最小化危险区以实现威胁规避。进一步的，考虑到在轨航天器执行任务需求，要求在轨航天器在完成威胁规避的同时能够回到原轨道，求解最优脉冲机动方案。

设来袭航天器最大机动能力（最大速度脉冲）为Δvmax，c，在轨航天器不采取任何机动时存在至少一段危险轨道区段，且危险轨道区段的危险系数为ξD，时间窗口匹配性为ξT。

在轨航天器采用多脉冲机动变轨对危险区进行避让，相邻脉冲之间最小时间间隔为δt。进行机动避让后的在轨航天器轨道危险系数为ξ'D，时间窗口匹配性为ξ'T。

3.1 优化变量

多脉冲机动规避策略优化变量取为脉冲施加时刻ti(i=1，2，…，n)和施加脉冲矢量Δvi(i=1，2，…，n)，在在轨航天器LVLH 坐标系中，Δvi可以表述为

式中：n为脉冲次数，优化变量共4n个。

假设在轨航天器在机动轨道上通过两脉冲机动与原轨道交会，则2 次变轨的速度增量可通过Lambert 算法求得。

3.2 约束条件

本文只考虑在轨航天器一个轨道周期T=内的威胁规避机动策略求解。对于t＞T时的规避机动，可基于T时刻的轨道状态重新求解轨道危险系数和时间窗口匹配性，再进行优化求解。

由于在轨航天器机动能力受限，因此脉冲施加时刻ti满足

式中：ti表示相对初始时刻脉冲时间。

由于危险区的威胁程度不仅与危险区比例ξD有关，其实际拦截可行性还与时间窗口匹配性ξT相关。为实现对来袭航天器的威胁规避，将危险系数和时间窗口匹配性设为约束条件：

若在轨航天器在机动轨道上通过两脉冲变轨回到原轨道，则在式（27）和式（28）的基础上需增加轨道瞄准约束，即最后一次脉冲后在轨航天器轨道根数满足

式中：Ei(tn)为在轨航天器进行i次机动后在tn时刻的轨道根数。

3.3 目标函数

优化目标为最小化燃料消耗，即

3.4 优化模型和算法

接近威胁规避策略优化模型为

选择差分进化（Differential Evolution，DE）算法［31］作为多脉冲机动主动规避策略的优化方法。

4 仿真分析

根据轨道危险区和威胁评价指标的定义可知，在轨航天器轨道危险区的存在性及受威胁程度由两航天器轨道关系及来袭航天器机动能力决定，因此本文提出的方法适用于任意两航天器轨道为圆轨道或椭圆轨道的情况。下面给出仿真结果以验证该方法的有效性。

4.1 在轨航天器轨道危险区仿真算例

本小节给出在轨航天器轨道危险区仿真结果，分别考虑在轨航天器与来袭航天器不在同轨道面和处于同轨道面的情况。

设来袭航天器初始轨道根数如表1所示，航天器在当前位置采取脉冲机动，机动量最大值=300 m s，机动方向任意，所得单脉冲机动可达域仿真结果如图9所示。图9 中，深绿色网格区域为来袭航天器机动可达域。

表1 来袭航天器初始轨道根数Table 1 Initial orbital elements of chaser

图9 在轨航天器轨道与来袭航天器可达域位置关系Fig.9 Geometry of chaser’s RD and target’s orbit

设在轨航天器初始轨道根数如表2所示，其中在轨航天器2 与来袭航天器处于相同轨道面上。

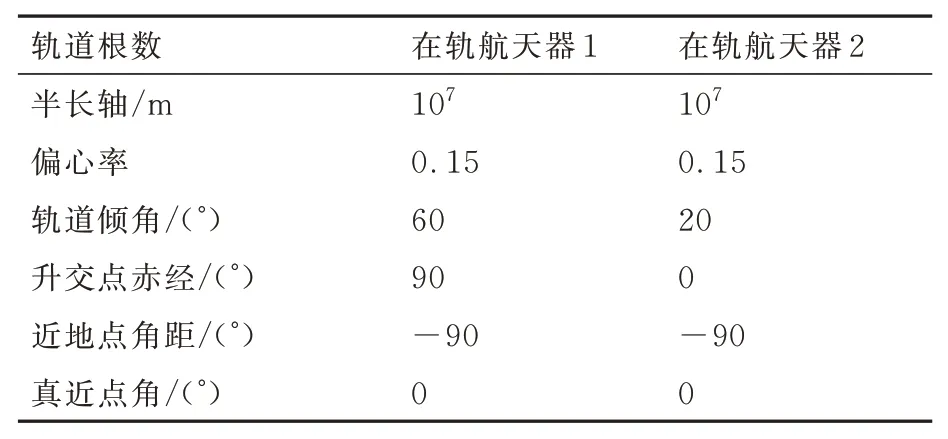
表2 在轨航天器初始轨道根数Table 2 Initial orbital elements of target

通过二体轨道外推，可得在轨航天器1 轨道如图9 和图10 中浅绿色轨道所示。图10 中，在轨航天器1 的2 段危险区的位置分别如图中红色区段和蓝色区段所示。

图10 在轨航天器1 轨道危险区Fig.10 Orbital danger-zone of Target 1

可知在轨航天器1 经过来袭航天器机动可达域且存在2 段危险区，其进出危险区的时间窗口和来袭航天器进出危险区的时间窗口估计见表3。基于危险区比例的危险系数ξD和时间窗口匹配性系数ξT计算结果见表4。

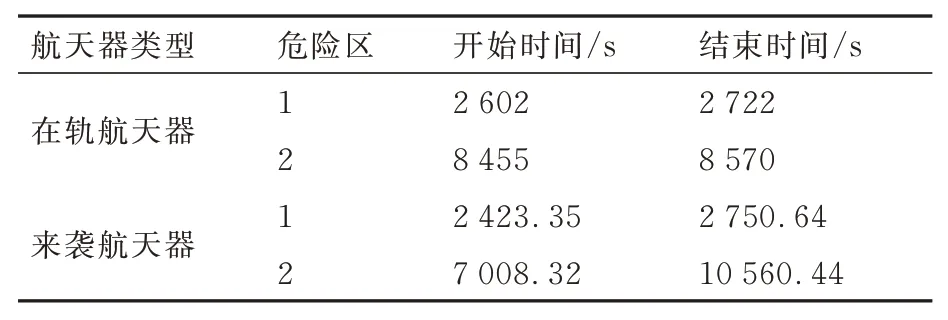
表3 到达危险区时间窗口Table 3 Time-window of danger-zone

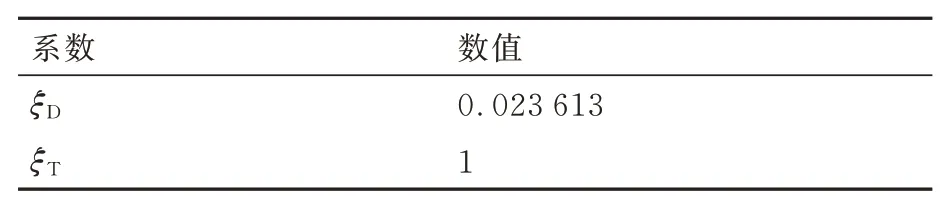
表4 危险系数ξD 和时间窗口匹配性系数ξTTable 4 Danger index ξD and time-window matching index ξT

分析图10 可知，2 段危险区在来袭机动平台可达域内的分布具备一定对称性，间隔约半个轨道周期。经计算来袭航天器初始轨道的运行周期为Tv=9 952.01 s，结合表3 数据可知，来袭航天器2 次到达危险区的时间间隔为7 008.32 s-2 423.35 s=4 584.97 s，验证了所提危险区求解算法的正确性。

图11所示为在轨航天器2 的轨道危险区。此时，两航天器进出危险区的时间窗口及基于危险区比例的危险系数和时间窗口匹配性系数计算结果分别如表5 和表6所示。

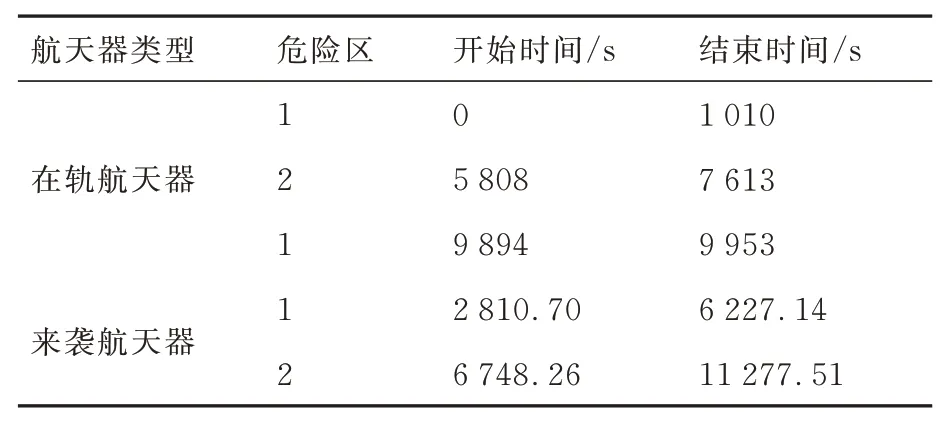
表5 到达危险区时间窗口（共面情况）Table 5 Time-window of danger-zone（coplane case）

表6 危险系数ξD 和时间窗口匹配性系数ξT（共面情况）Table 6 Danger index ξD and time-window matching index ξT（coplane case）

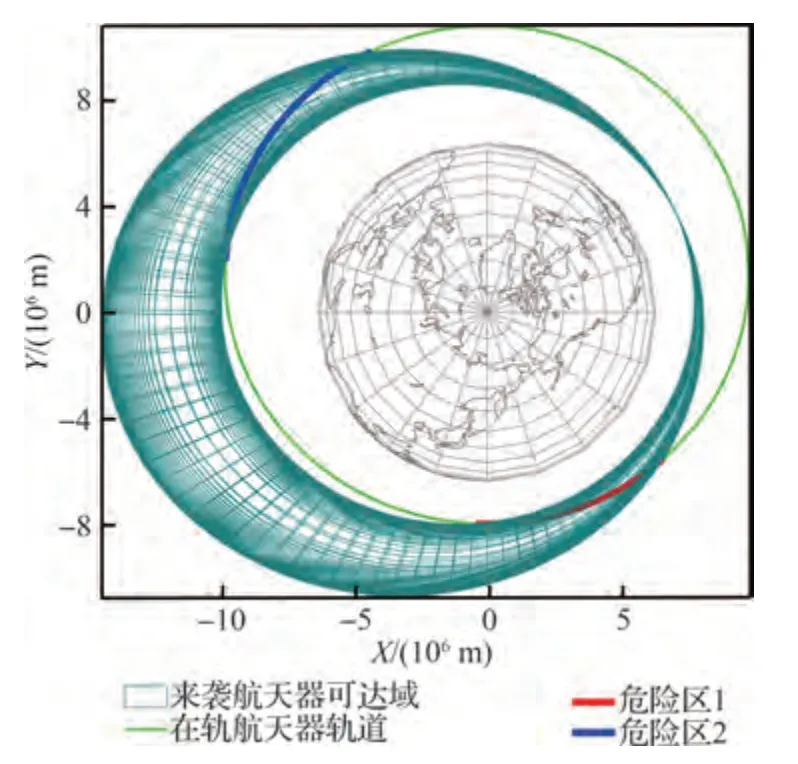
图11 在轨航天器2 轨道危险区Fig.11 Orbital danger-zone of Target 2

由表5 和表6 可知，由于在轨航天器2 与来袭航天器处于相同的轨道平面，其轨道危险区范围远大于在轨航天器1 的轨道危险区范围。

4.2 多脉冲机动主动规避仿真算例

设来袭航天器初始轨道根数如表1所示，在轨航天器初始轨道根数如表2所示。来袭航天器在t=0 s 时刻采取脉冲机动，脉冲机动最大值=300 m s，机动方向任意。经计算，优化前在轨航天器存在2 段危险区，基于危险区比例的危险系数ξD=0.023 613，时间窗口匹配性系数ξT=1。

设在轨航天器相邻脉冲最小时间间隔Δt=10 s。按照上述设置，可求解在轨航天器多脉冲机动威胁规避策略。

4.2.1 不考虑与原轨道的交会约束

不考虑与原轨道交会的约束时，基于式（31）的优化模型可以求得多脉冲机动威胁规避优化策略，结果如表7所示。以两脉冲机动规避策略为例，优化后的威胁规避机动轨道如图12 和图13所示。

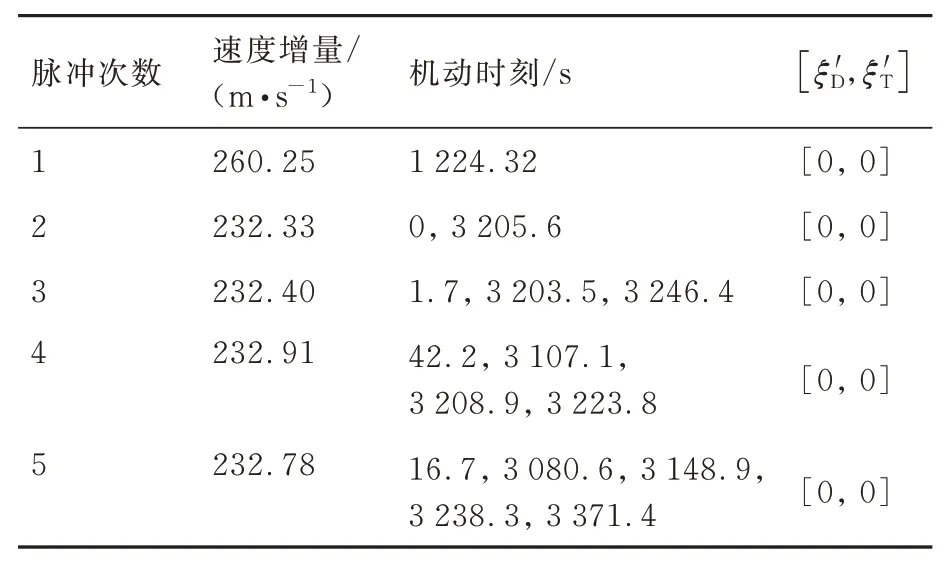
表7 多脉冲机动优化结果（不考虑交会约束）Table 7 Optimal results of multi-impulses （without rendezvous constraint）

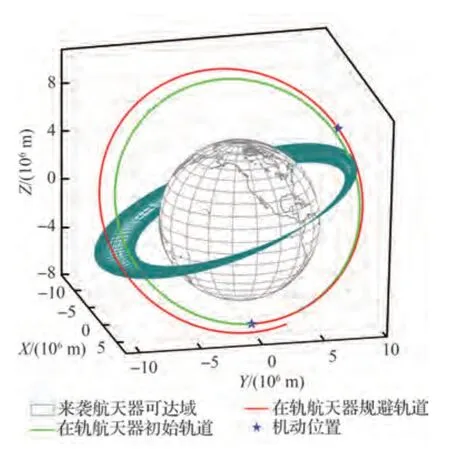
图12 在轨航天器机动轨道与来袭航天器可达域位置关系（不考虑交会约束）Fig.12 Geometry of chaser’s RD and target’s maneuvering orbit （without rendezvous constraint）

图13 Y-Z 平面在轨航天器规避轨道与来袭航天器可达域位置关系（不考虑交会约束）Fig.13 Geometry of chaser’s RD and target’s maneuvering orbit in Y-Z plane（without rendezvous constraint）

从图12 和图13 中可以看出，不考虑交会约束时，在轨航天器威胁规避机动轨道与来袭航天器可达域不存在重合区段，即危险系数ξ'D=0。对比表7 中多脉冲机动规避策略求解结果，有，即当脉冲次数＞2 时，在轨航天器进行威胁规避所需速度增量相差不大，因此可采取两脉冲机动作为威胁规避方案。

此外，通过对比多个机动方案中所求速度增量发现，其垂直轨道面方向的速度分量远小于轨道面内的速度分量，这是由于轨道危险区在在轨航天器轨道面内导致的。

4.2.2 考虑与原轨道的交会约束

在4.2.1 节的基础上，考虑与原轨道交会的约束，多脉冲机动规避策略求解结果如表8所示。以四脉冲机动为例，优化后的转移轨道如图14 和图15所示。从图14 和图15 中可以看出，考虑交会约束时，在轨航天器威胁规避机动轨道与来袭航天器可达域仍存在重合区段，但双方不满足时间匹配关系，即危险系数ξ'D≠0、时间窗口匹配性系数ξ'T=0。

图14 在轨航天器机动轨道与来袭航天器可达域位置关系Fig.14 Geometry of chaser’s RD and target’s maneuvering orbit

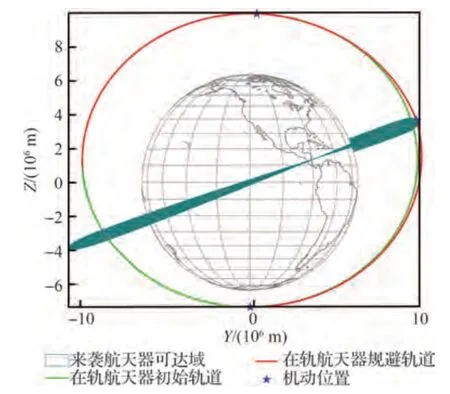
图15 Y-Z 平面在轨航天器机动轨道与来袭航天器可达域位置关系Fig.15 Geometry of chaser’s RD and target’s maneuvering orbit in Y-Z plane

对比表8 中多脉冲机动规避策略求解结果可知，增加脉冲次数并不能减小考虑交会约束时的威胁规避机动方案所需速度增量，因此可采取三脉冲机动作为威胁规避方案。

5 结 论

基于轨道机动可达域分析提出了机动航天器接近威胁计算、评估和规避方法。

1） 通过判断在轨航天器自身轨道与来袭航天器机动可达域间的位置关系计算其位于威胁域内的区段，得到轨道危险区。

2） 基于两航天器进出危险区的时间定义了威胁评价指标，分别从空间和时间窗口匹配性角度评估在轨航天器受来袭航天器的威胁程度。

3） 给出的基于最小化危险区的航天器多脉冲机动主动规避策略，能够实现对危险区的机动避让。

仿真结果表明，基于本文方法在轨航天器能够在满足给定约束条件下实现对危险区的机动规避。

致 谢

感谢载人航天工程科技创新团队（Technology Innovation Team of Manned Space Engineering）对本文的支持。