山区陡坡桥梁桩基受力与变形分析

摘要 文章针对山区陡坡桥梁桩基的受力与变形问题，建立数学模型，提出了求解方法。通过分析群桩的受力作用，推导出滑坡推力分布公式，计算了桩周土抗力和桩间土压力。基于有限差分法的分析，得到承载段、嵌岩段和自由段的挠曲变形微分方程，并根据边界条件求解。实例结果表明：计算结果与实际测量基本吻合，验证了计算公式的有效性，为实际工程中的桩基设计和分析提供了重要的解决方案。

关键词 山区陡坡桥梁桩基；滑坡推力分布；有限差分法；受力与变形

中图分类号 U414.4 文献标识码 A 文章编号 2096-8949（2024）04-0090-03

0 引言

山区陡坡给桥梁的安全带来巨大挑战。该文深入研究桩基在复杂地形条件下的受力特点、变形规律及应对自然灾害的能力，为桥梁的设计、施工和后期运营提供了理论依据，确保了桥梁在复杂地形环境中的安全可靠性^[1]。围绕山区陡坡桥梁桩基受力与变形进行深入研究，并提出相应的数学模型和求解方法，得到准确和可靠的结果。

1 复杂荷载条件下山区陡坡桥梁桩基受力模型

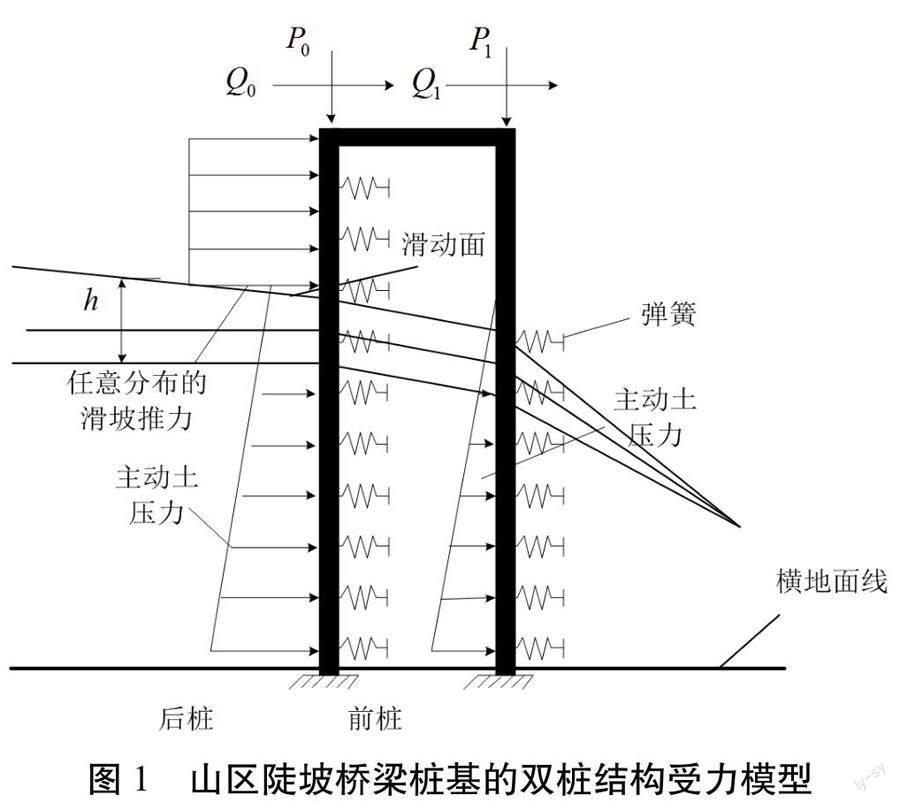
在外部荷载作用下，桥梁桩基的受力复杂。建立合适的数学模型准确预测桩基在各种荷载条件下的力学响应，确保桩基在设计范围内安全可靠。对桩基的受力分布和强度进行详细分析，优化结构设计，选择合适数量和合适尺寸的桩来承担复杂荷载的作用，提高整体结构的稳定性，如图1所示。

假设桩基桩顶不会发生转角变形，将上部结构对桩顶作用的荷载等效为两个作用力P和Q，h为滑动面高度。此外，将桩基与桩前土体之间的相互作用近似弹性支撑关系，一般情况下，将其划分为两个部分：滑动面之上的桩体受到滑坡推力的作用，而滑动面之下的桩基则受到土体线性分布的土压力作用，能更好地研究桩基的受力特性^[2-3]。

1.1 滑坡推力分布规律

滑坡推力是指滑坡负荷对土体所产生的剪应力。通过建立滑坡推力分布规律模型，确定桥梁桩基承受的滑坡推力的大小和分布，为桩周土抗力计算提供基础数据^[4]。桩后坡体的滑坡推力分布形式通常以简化的几何形状来表示，滑坡推力的通用公式如式（1）：

p（h）=ξh²+p₀（1）

式中，h——滑坡高度；ξ——土壤的单位重量；p₀——主动土压力。

1.2 桩间土压力计算

在山区陡坡桥梁桩基设计中，桩间土压力较大，计算桩间土压力对桥梁稳定性和桩基受力至关重要，是指导桩基的设计和施工的依据。分析后排和前排桩的受力状态时，应考虑其中一侧没有桩体而是完整的滑坡体的情况，假定滑坡后没有桩体时的土压力为σ_a由于后排桩的存在，应综合考虑滑坡推力的范围和两排桩之间的距离，以削减当前桩身所受到的压力。d₀表示桩体和滑动面边缘的距离，表达式为：

式中，σ'_a為前桩实际受到的土压力；W₁表示桩间土重量；W₁₁表示滑体重量。

2 山区陡坡桥梁桩基受力与形变分析

2.1 受力分析有限差分方程

基于以上分析计算，全面了解桩基在复杂荷载下的受力作用，为进一步分析山区陡坡桥梁桩基受力与变形提供理论基础。桩基微元受力分析可以将桩基看作由一系列微小单元组成的连续体，在每个微元上进行受力分析。对桩基的受力分布进行精细化计算，更准确地了解桩基受力的特点和规律。通过桩基微元受力分析，更准确地理解桩基受力与形变的关系，可以对桩的类型、数量、直径和间距等参数进行优化设计，确保桩基的稳定性和安全性，降低工程造价。选取桥梁桩基中的一段微元进行受力分析，如图2所示。

对图2中的基桩微元体下端中点取矩可得：

进行桩身的受力分析应该考虑不同段落的弯矩和剪力对基桩的影响。具体如下：

（1）嵌岩段，对于嵌岩段基桩，其下方直接嵌入岩石中，并且在岩石与桩侧土之间存在较高的摩擦阻力。因此，在嵌岩段基桩中，除了考虑桩顶和桩底的边界条件外，还需要考虑岩石—桩侧土界面的约束条件以及对位移和应力传递的影响。

（2）自由段，自由段基桩指的是桩段位于土体中无明显侧向约束条件的部分。在自由段中，由于缺乏侧向支撑，其受力机制和挠曲行为与承载段基桩有所不同。

2.2 边界条件

在实际工程中，桥梁桩基常常被打入基岩深处，桩底可以被认为是固支的，具有一定的约束条件。桩顶通常是无约束的，只受到外部施加的力矩作用。用下述方式重新表达桩顶和桩底的边界条件：

2.2.1 桩顶自由

式（6）表示桩顶的边界条件，即桩顶是自由的，没有受到约束。在实际工程中，桩顶通常暴露在土层表面或嵌入浅层土中，不受约束，因此该边界条件可视为桩顶自由。

2.2.2 桩端嵌固

一般桩基深入基岩以下，主要依靠基岩来提供支撑能力。由于桩底与基岩直接接触，基岩的刚度和强度对桩底的受力和变形起到至关重要的作用。因此，将桩底的边界条件视为桩端嵌固条件。考虑基岩的力学性质对桩底受力和变形的影响，确保在分析中充分考虑桩底嵌固的特性，有助于更准确地模拟和分析整个桩体的受力和变形情况，为桩基设计与工程实践提供了重要的理论支持。

边界条件不仅影响着基桩局部受力的传递和分布，也反映了桩顶与土体的接触情况以及桩底与基岩之间的相互作用。考虑边界条件，更加真实地模拟和分析桩基的受力和变形，使所建立的数值模型更贴近实际工程，确保基桩在复杂地形和荷载条件下的稳定性和可靠性。

2.3 有限差分求解

采用有限差分法求解基桩单元微分方程式，即可得到桥梁桩基内力和位移结果。采用等量分段，每段长为h，自桩顶至桩底将全桩离散成N分段。

承载端控制差分方程为：

应用相同的方法来推导自由段和嵌固段的差分方程，并计算出每个节点的位移，可以实现对基桩不同部分的变形情况进行计算。综合考虑桩顶和桩底的边界条件，确保各个特征桩段之间内力和变形的协调，有助于解出基桩的桩身变形和内力分布情况。基于以上分析，计算出基桩的桩身转角、弯矩和剪力值，进一步理解桥梁桩基的内力分布和变形规律，为桥梁结构的设计提供重要理论依据，确保桩基在复杂荷载作用下的安全性和稳定性。

3 实例分析

为了验证公式的准确性，选择某高速公路大桥斜坡处桥梁桩基作为实例。该大桥为双幅桥，其中左幅桥梁起讫桩号为ZK28+920～ZK30+080，全长1 160 m；右幅桥梁起讫桩号为YK28+920～YK30+380，全长1 460 m。在项目现场开展实地调查和数据采集，获得现场工程条件下桩基受力与变形的现场数据，实测数据作为基础数据验证上述模型。桥址处桥梁桩基及桥址高边坡现场情况如图3～4所示。

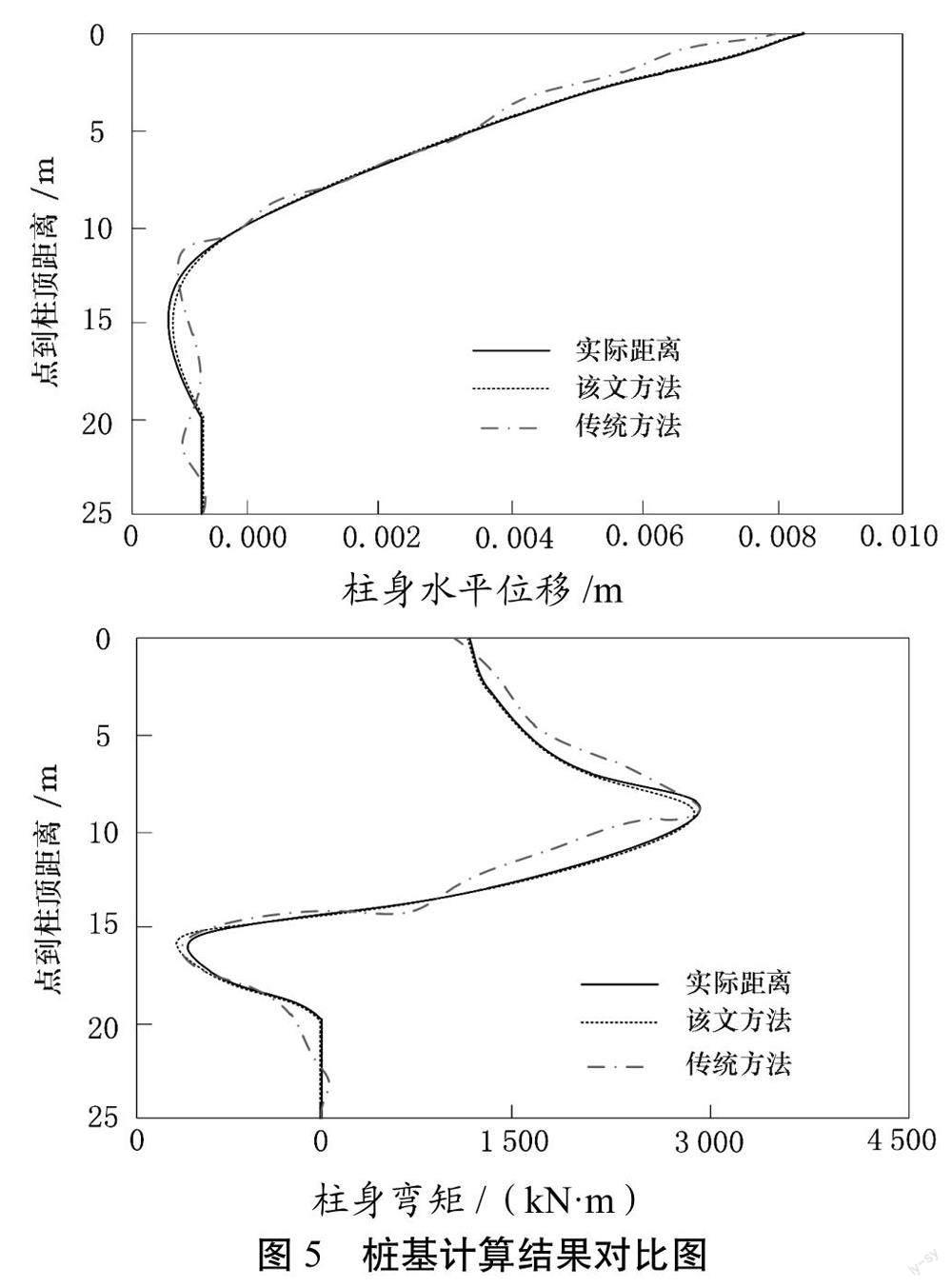
将桥梁桩基位移与弯矩计算结果进行对比，通过对基柱位移与弯矩的计算可以验证所采用的数值模型的准确性和可靠性。对比结果如图5所示。

理论计算结果与实际观测结果基本吻合，验证了方法的有效性和可靠性。传统方法明显出现较大差距，由于传统方法在对参数、模型以及边界条件的选择上存在一定的局限性。该文经过详尽的研究和验证，针对工程实际情况进行了充分的模拟，能够更准确地反映实际桩基受力与变形情况。通过对参数、模型及边界条件的真实模拟和论证，表明该文方法在山区陡坡桥梁桩基受力与变形分析中具有一定的工程应用价值。

4 结论

通过滑坡推力分布规律的推导、桩周土抗力和桩间土压力的计算，能够合理评估桩基受力情况。该文基于有限差分法的分析，得到了承载段、嵌岩段和自由段的挠曲变形微分方程，并考虑桩顶自由和桩端嵌固的边界条件。最后，采用有限差分法对桩基内力和位移进行求解，验证了该文方法的准确性和可靠性。通过研究，能够更深入地理解山区陡坡桥梁桩基的受力与变形机制，为山区桥梁桩基的设计和优化施工方案提供理论支持，对提高桥梁结构安全性和降低工程造价具有重要价值。

参考文献

[1]刘小林. 复杂土层条件下堆载对邻近桥梁桩基受力变形的影响及控制研究[J]. 五邑大学学报（自然科学版）， 2023（1）： 71-78.

[2]宋剑， 张蛟， 成进科， 等. 抗滑桩对桥梁桩基受力变形影响的模型试验研究[J]. 公路， 2022（4）： 118-124.

[3]葛志平， 李中浩， 奚晓广， 等. 堆载作用对桥梁桩基位移的控制技术研究[J]. 山西建筑， 2021（12）： 137-139.

[4]祝彥知， 赵雅纯， 田光辉， 等. 考虑冲刷和材料劣化耦合作用的钢筋混凝土桥梁桩基承载性能研究[J]. 水利水电技术（中英文）， 2023（3）： 116-125.

收稿日期：2023-12-06

作者简介：杨耀宗（1989—），男，硕士研究生，工程师，研究方向：桥梁与隧道工程。