基于粒子群优化算法的新能源车充电站选址策略研究

肖志良 汪丽娟 郑雁予

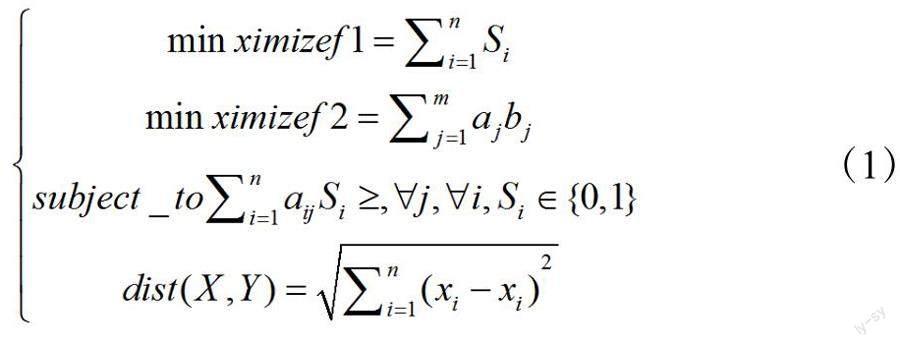
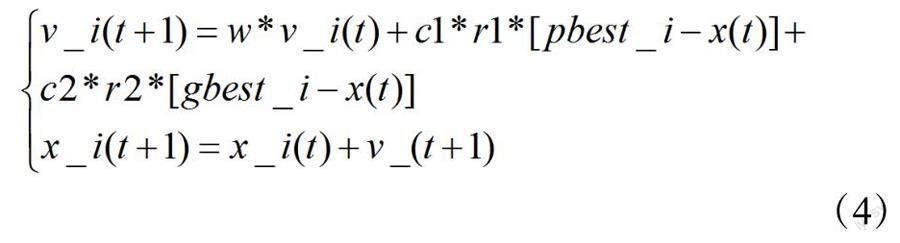
摘要 为解决传统电动汽车充电站选址效率不高、易陷入局部最优的问题，文章研究方法在标准粒子群优化算法的基础上，通过多种群协同进化、动态调整参数和引入混沌搜索等手段对粒子群优化算法进行改进。实验结果表明，在第二种广义惩罚函数中，IPSO、WOA、TS以及PSO四种算法分别收敛于第160次迭代、第80次迭代、第90次迭代、第390次迭代。IPSO的适应度最小值为?15.5。综合来看，IPSO算法在两个测试函数上的优化性能都相对较好，具有较低的适应度最小值和较快的收敛速度。

关键词 粒子群优化算法；新能源汽车；充电站选址

中图分类号 U491.1+4 文献标识码 A 文章编号 2096-8949（2024）04-0038-03

0 引言

随着全球对可持续发展的关注不断增加，新能源车的普及正成为减少污染和依赖传统能源的重要途径，新能源车充电站选址问题直接影响充电站的利用率、用户的充电便利性以及充电网络的整体效益^[1]。近年来，粒子群优化算法（Particle Swarm Optimization，PSO）成为一种备受关注的全局优化算法^[2-3]。PSO算法受到了自然界群体智能行为的启发，通过模拟粒子在解空间中的位置和速度来搜索最优解。这种算法具有全局搜索能力和较好的收敛性，能够快速有效地找出充电站的最佳位置和布局。然而，由于充电站选址问题的复杂性和多样性，传统的方法在解决这一问题上存在效果差、容易陷入局部最优的问题。鉴于此，该研究在粒子群优化算法的基础上，结合周边的兴趣点、需求点以及建设成本等因素，设计选址的目标函数。通过多种群协同进化、动态调整参数和引入混沌搜索来对传统PSO算法进行优化，期望通过这种方法，为新能源车充电站选址问题提供一种高效、可行的解决方案，促进新能源车的普及和可持续发展。

1 粒子群优化算法改进及充电站选址模型构建

粒子群优化算法（Particle Swarm Optimization，简称PSO）是一种基于群体智能的全局优化算法，灵感来自鸟群或鱼群等群体行为的观察。PSO算法通过模拟群体中个体之间的协作和信息共享来寻找最优解。在新能源车充电站选址中，粒子群优化算法的具体应用优势体现在四个方面^[4]：第一，它能充分考虑充电需求，通过优化算法可以更准确地预测充电站的充电需求量，从而为充电站的规模和设备配置提供科学的依据。第二，它能降低建设成本，通过优化算法，可以在满足充电需求的前提下，降低充电站的建设成本，提高充电站的经济效益。第三，全局搜索能力强，PSO算法通过模拟鸟群觅食行为，在搜索空间中不断调整粒子的速度和位置，从而能够较好地探索整个搜索空间，寻找全局最优解。这对于充电站选址问题来说，能够帮助找到最佳的位置，使得充电站的布局更加合理和高效。第四，并行计算能力强，粒子群优化算法的每个粒子的搜索都是独立的，因此可以进行并行计算，提高算法的计算效率。这对于大规模的充电站选址问题来说，能够加快搜索速度，提高算法的运行效率。基于粒子群优化算法的新能源车充电站选址策略优化模型的算法流程如下：

明确问题的目标和约束条件。例如，确定新能源汽车充电站的最佳位置，以最小化用户的行驶距离和充电时间为目标，同时考虑充电站的供电能力和建设成本等约束条件。在构建电动汽车充电站的过程中，必须全面考虑多个目标的约束条件，以确保能够满足各方的利益需求，并保障充电站建设的经济效益和可持续性^[5]。

首先，为了更好地满足用户的充电需求，新的充电站应选址在其周边的兴趣点（POI）方便的位置。这意味着需要充分考虑充电站周边POI的分布和密度，以及用户的出行规律和充电需求。通过深入研究和估计未覆盖的POI的充电需求，可以更准确地预测充电站的充电需求量，从而为充电站的规模和设备配置提供科学的依据。最大化覆盖POI数量的定义如式（1）所示：

式中，S_i——该选址处是否被选择；n——选址数量；m——未覆盖的周边的兴趣点数量，若某选址能覆盖到POI则a_ij=1，若某选址能覆盖到需求点则b_j=1。

其次，为了避免资源浪费和恶性竞争，新的充电站应尽量避免与现有的和其他新的充电站覆盖区域重叠。最小化与需求电动汽车的距离可以定义为式（2）：

式中，cost——单个充电设备的成本；n——该选址需要的总充电设备数量；f 1、f 2、f 3将构成粒子群优化算法的目标函数。第一步初始化粒子群，随机生成一群粒子，每个粒子代表一种可能的充电站布局方案。每个粒子的位置表示充电站的位置。第二步计算适应度，根据已定义的目标函数，计算每个粒子的适应度值。适应度值反映了充电站布局方案的优劣程度。第三步更新粒子的个体最优解，对于每个粒子，根据当前的适应度值，更新粒子的个体最优解。个体最优解是粒子自身经验中最优的充电站布局方案。粒子的速度和位置的更新公式如式（4）所示：

式中，v_i（t）——粒子i在时刻t的速度；x_i（t）——粒子i在时刻t的位置；pbest_i——粒子i的个体最优解；gbest_i——群体中的全局最优解；w——惯性权重；c₁、c₂——加速因子；r₁、r₂——随机数。第四步是更新全局最优解，根据当前的适应度值，更新全局最优解。全局最优解是整个粒子群中适应度值最好的充电站布局方案。第五步更新粒子的速度和位置，根据粒子群算法的公式，更新每个粒子的速度和位置。速度的更新受到个体最优解和全局最优解的吸引，并受到惯性权重的控制。第六步判断停止条件，判断是否满足停止条件，是否达到最大迭代次数或找到满足要求的解。然后进行迭代更新，如果停止条件未满足，返回步骤3继续迭代，更新粒子的适应度、个体最优解、全局最优解和粒子的速度和位置。最后输出结果，当满足停止条件后，输出全局最优解作为新能源车充电站的最佳位置布局方案。粒子群优化算法在充电站选址优化中的应用虽然有很多优点，但也存在一些缺点，例如容易陷入局部最优、对参数敏感等。为了克服这些缺点，研究引入一系列优化措施。首先是多种群协同进化，为了避免算法陷入局部最优，采用多种群协同进化的策略。具体来说，就是将种群分成多个子种群，每个子种群采用不同的参数设置和搜索策略进行进化，并定期交换信息。这样可以增加种群的多样性，避免算法陷入局部最优。其次，针对粒子群优化算法对参数敏感的问题，采用动态调整参数的策略。具体来说，就是在算法的运行过程中，根据种群的进化情况和搜索进度，动态地调整惯性权重、学习因子等参数的值。这样可以提高算法的适应性和求解性能。最后，为了增强算法的全局搜索能力，可以引入混沌搜索的策略。具体来说，就是在算法的运行过程中，以一定的概率在搜索空间内随机生成一些新的粒子，并用混沌映射的方式更新它们的位置和速度。这样可以增加种群的多样性，提高算法的全局搜索能力。通过以上的算法流程，基于粒子群优化算法的新能源车充电站选址策略优化模型能够帮助找到最佳位置，并優化充电站的布局，从而提高充电效率和用户体验。

2 模型性能測试与对比实验

为解决电动汽车充电站选择优化模型易陷入局部最优的问题，研究基于粒子群优化算法，进行了一系列改进，最终设计出IPSO算法。为验证该算法在充电站选址问题中的适用性，研究引入鲸鱼优化算法（Whale Optimization Algorithm，WOA）、禁忌搜索算法（Tabu Search，TS）与标准PSO算法进行对比实验，通过阿利克函数和第二种广义惩罚函数计算上述四种算法的收敛曲线，实验结果如图1所示。

由图1（a）可知，在第二种广义惩罚函数中，IPSO、WOA、TS以及PSO四种算法分别收敛于第160次迭代、第80次迭代、第90次迭代、第390次迭代。IPSO的适应度最小值为?15.5。而其他三种算法的适应度均收敛于?8左右。由图1（b）可知，在阿利克函数中，IPSO、WOA、TS以及PSO四种算法分别收敛于第70次迭代、第390次迭代、第190次迭代、第20次迭代。IPSO的适应度最小值为?12.5。而其他三种算法的适应度分别收敛于?11.3、?11.6、1.3。综合来看，IPSO算法在两个测试函数上的优化性能都相对较好，具有较低的适应度最小值和较快的收敛速度。为探究IPSO算法在实际运用中的效果，研究从高德地图中获取了成都市主城区现有电动汽车充电站分布数据以及电动汽车分布数据。并将该算法应用于实际的选址优化中，实验结果如图2所示。

图2（a）揭示了成都市当前电动汽车充电站的分布格局，明显看出，电动汽车在这座城市的普及度已相当广泛。然而，现有的充电基础设施显然未能与庞大的充电需求相匹配，呈现出一种供不应求的状态。这种情况可能会对电动汽车的进一步普及和使用便利性产生制约影响。图2（b）则进一步展示了应用IPSO算法进行充电站选址优化后的推荐方案。经过精细化的算法处理，这些被推荐的选址地点呈现出人流高度集中和充电需求量大的特点，与预期中的优化效果相符。这一结果验证了IPSO算法在解决此类复杂选址问题上的有效性和优越性，同时也为成都市未来充电基础设施的规划和建设提供了有价值的参考依据。

3 结论

为优化新能源汽车充电站选址策略，研究提出了一种基于粒子群优化算法的充电站选址模型。实验结果表明，在广义惩罚函数和利克函数对比测试中，IPSO相较于WOA、TS和PSO算法具有更适中的迭代次数和更小的适应度值，其迭代次数最少分别为160次和70次，适应度最小值分别为?15.5和?12.5。综合来看，IPSO算法在两个测试函数上的优化性能都相对较好，具有较低的适应度最小值和较快的收敛速度。通过应用性分析可以发现，经过精细化的算法处理，这些被推荐的选址地点呈现出人流高度集中和充电需求量大的特点，与预期中的优化效果相符。综上所述，研究提出的IPSO新能源汽车选址模型具有收敛速度快、适应度高等优点，但该模型尚未考虑到建设地点的交通流量情况，这也是后续研究需要改进的方面。

参考文献

[1]张文会， 苏嘉祺， 哈字洪， 等. 电池交换式纯电动公交充电站选址定容模型[J]. 华南理工大学学报（自然科学版）， 2023（10）： 126-134.

[2]李宏玉， 张孝民， 姜晨辉， 等. 基于改进飞蛾扑火算法的电动汽车充电站选址[J]. 电气自动化， 2023（5）： 113-114+118.

[3]梁露， 韩飞. 考虑排队时间和充电费用的电动汽车充电站选址模型[J]. 交通信息与安全， 2023（4）： 154-162.

[4]曾颖娇， 张邻， 徐家楠， 等. 三网融合下的电动汽车充电站规划方案综合评价[J]. 现代工业经济和信息化， 2023（6）： 123-127+130.

[5]Deng W， Xu J， Zhao H， et al. A novel gate resource allocation method using improved PSO-based QEA[J]. IEEE Transactions on Intelligent Transportation Systems， 2020（3）： 1737-1745.

收稿日期：2023-12-05

作者简介：肖志良（1965—），男，博士研究生，高级工程师，研究方向：物联网应用技术。

基金项目：广东省教育厅2021年度普通高校重点科研平台项目“物联网应用技术创新团队”（2021KCXTD074）。