外伸横梁宽幅钢箱梁桥空间受力分析

胡国栋 梅霄云

摘要 文章介绍了（6.42+47.4+6.42）m简支宽箱钢箱梁桥的设计方案。利用Midas Civil软件建立了全桥单梁模型和梁格模型，同时建立板单元模型对梁格模型进行了验证。进行了承载能力极限状态主梁体系验算，对比了纵梁不同梁高和板厚条件下的受力情况，分析了宽箱钢箱梁单梁模型、梁格模型和板单元模型的计算结果。

关键词 宽箱钢箱梁；单梁模型；梁格模型；板单元模型；主梁体系验算

中图分类号 U441.5 文献标识码 A 文章编号 2096-8949（2024）04-0071-04

0 引言

随着现代城市的高速发展，城市桥梁在设计中既要满足通行功能，还应保证与所在地区自然景观、人文环境等相协调，钢箱梁桥以其抗拉强度高、自重小、跨越能力大、施工期限短等优势而备受青睐^[1]。为满足交通流量日益增大的需要，城市立交桥梁也开始广泛采用长悬臂宽箱梁断面，这种结构形式受力极其复杂，且表现出较大的空间变形和受力特性^[2]。同时，由于桥面宽度较大，桥面板应力分布不均匀，常规梁理论无法精确分析其力学特性。因此，采用板单元模型对梁单元模型的计算结果进行验算是極其必要的^[3-4]。

该文通过对（6.42+47.4+6.42）m简支宽箱钢箱梁上部结构分别建立单梁、梁格模型进行受力分析，并建立板单元模型对梁格模型的计算结果进行了验证，还对比了不同梁高和板厚情况下梁格模型的计算结果，以期为今后钢箱梁的设计与施工提供参考。

1 工程概况

该工程方案桥梁全长61.34 m，为跨径（6.42+47.4+6.42）m简支钢箱梁，主梁梁端设置牛腿，布置跨径4.5 m钢板梁连接钢箱梁与地下空间顶板道路。桥梁正交布置整幅设计，桥面总宽47 m。简支钢箱梁采用单箱八室直腹板截面，梁顶标准宽4 700 cm，梁底标准宽4 000 cm，梁高192 cm；箱梁悬臂板长350 cm，悬臂厚度一次变化，端部厚32 cm，根部厚80 cm。箱梁顶面设置1.5%横坡，人行道设置2%单向反坡。桥面铺装采用7 cm沥青混凝土+8 cm钢纤维混凝土，桥面铺装总厚度15 cm。钢箱梁标准断面见图1。

2 设计思路

结合该桥路段的实际情况，道路红线宽度60 m，桥梁上跨河道，下方地下二层为轨道交通，根据轨道交通限界要求，桥墩不得侵入道地下空间范围内，同时根据河道断面形式，该工程方案定为跨径（6.42+47.4+6.42）m简支梁，桥梁桩基承台随地下空间一并预埋施工。桥梁位置处横断面左右侧去掉绿化带，横向布置为47 m=7 m（人行道）+2.5 m（非机动车道）+1.5 m（机非分隔带）+11.5 m（机动车道）+2 m（中央分隔带）+11.5 m（机动车道）+1.5 m（机非分隔带）+2.5 m（非机动车道）+7 m（人行道），桥面宽度较大，且采用宽箱大横梁（长52.4 m×宽3.8 m×高4.92 m），横向空间效应突出，单梁模型无法明确反映出边、中梁的受力差异，故采用梁格模型进行分析。同时，通过改变纵梁的梁高和板厚，探讨二者对体系受力的影响程度。

利用Midas Civil 2019软件，分别建立单梁模型（见图2）、梁格模型（见图3）和板单元模型（见图4）。模型中单元的几何特性、边界条件与实际结构保持一致。根据实际施工流程进行模拟计算分析。

3 纵梁梁高及板厚对钢梁空间受力影响分析

3.1 纵梁梁高对体系空间受力的影响

单梁模型1.92 m梁高内力计算结果见表1。

梁格模型内力计算结果见图5～6。

对比各模型的内力计算结果，可以得出如下结论：

（1）通过梁格法的计算结果可以看出，由于端横梁长度较大，荷载作用下产生竖向变形，导致中梁卸载，最中间梁弯矩及剪力最小，往边梁依次增加，体系空间效应显著。

（2）梁格模型1.92 m梁高9片纵梁弯矩叠加值为255 556 kN·m，与单梁模型相差1.67%；剪力叠加值23 654 kN，与单梁模型相差7.5%。二者受力情况接近，且与已有成熟的箱梁桥受力特性相符，可见两种方法都较好地模拟了实际工程的受力情况。

（3）在梁格模型梁高分别为1.92 m、2.2 m、2.5 m三种情况下，随着梁高的增加，跨中弯矩与支点剪力也逐渐增大。2号次边梁与5号中梁弯矩值分别相差10 990、12 893、14 976，幅度越来越大；1号边梁与5号中梁剪力比分别为2.23、2.68、3.28，可知一味增加梁高并不利于此结构受力，故最终取梁高1.92 m较为经济合理，此时梁高约为跨度的1/25。

3.2 纵梁板厚对体系空间受力的影响

单梁模型1.92 m梁高计算结果见表2。

不同梁高下梁格模型计算结果：

全桥共9片梁，该桥为对称结构，表中仅列出5片梁计算结果见表3（1号为边梁，2号为次边梁，3～5号为中梁）。

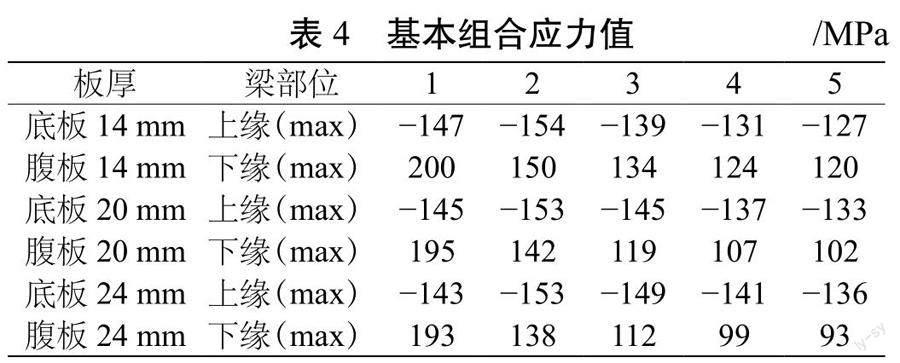
根据计算结果可以看出，1号边梁和2号次边梁所受拉、压应力最大，可知该体系主要为边梁受力，为进一步验证，取3～5号中梁不同板厚情况进行分析见表4。

通过分析各模型不同梁高、板厚的应力计算结果可得出以下结论：

（1）对比单梁模型和梁格模型的应力计算结果可知，以梁格模型的计算结果为基准，单梁模型上缘压应力计算结果与梁格模型1.92 m、2.2 m、2.5 m梁高计算结果最大值分别相差12%、0%、10%，单梁模型下缘拉应力计算结果与梁格模型1.92 m、2.2 m、2.5 m梁高计算结果最大值分别相差21%、11%、3%，且均满足规范要求。

（2）通过梁格模型不同梁高的计算结果可以看出，随着梁高的增大，主梁上、下缘拉、压应力值均逐渐减小，说明梁高的取值对体系的应力影响显著，设计中应结合规范取值、经济适用等要求，合理地选取梁高。

（3）通过比较梁格模型纵梁不同板厚的计算结果可以看出，随着中梁板厚的增大，主梁上、下缘拉、压最大应力值无明显改变，说明由于端横梁长度较大，荷载作用下产生竖向变形，导致中梁卸载，最中间梁上、下缘应力均最小，往边梁依次增加，该体系主要为边梁受力，增加中梁腹板及底板厚度对体系受力改善不明显，设计中应结合实际情况，对边梁、中梁的板厚进行不同取值，不但符合实际受力情况，而且节省了施工成本。

4 体系横向空间效应分析

考虑梁格模型实际为简化算法，存在一定的设计假定，建立板单元模型对梁格模型计算结果进行验证。

4.1 板单元应力计算结果

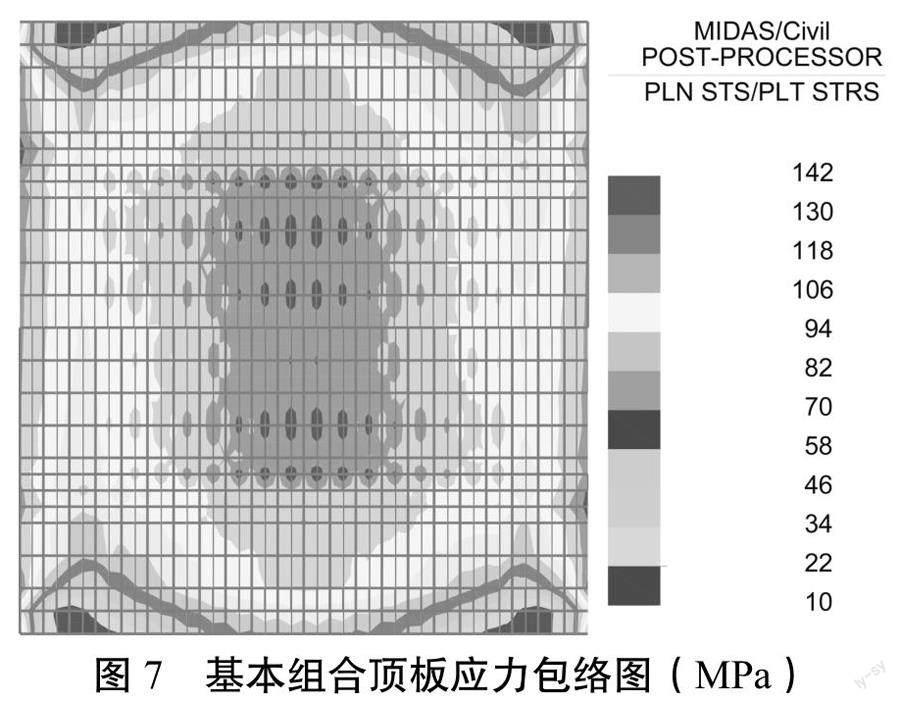
顶板正应力计算结果见图7。

底板正应力计算结果见图8。

板单元模型顶板基本组合最大正应力为142 MPa，底板基本组合最大正应力为185 MPa。

4.2 单梁模型、梁格模型、板单元模型计算结果对比分析

以1.92 m梁高的梁格模型为基准，各计算结果对比见表5。

通过以上表格可以看出，板单元模型与梁格模型1.92 m梁高计算结果相比：顶板应力相差3%；底板应力相差9%；边中梁剪力比相差6%；恒载位移相差0%；活载位移相差14%；标准组合反力值相差0%。二者计算结果基本吻合，都很好地模拟了该体系的空间受力情况。

5 结语

该文通过介绍（6.42+47.4+6.42）m简支宽箱钢箱梁桥的设计方案，利用Midas Civil软件建立了全桥单梁模型、梁格模型和板单元模型。通过对比计算结果可得出以下结论：

（1）宽箱钢箱梁桥的横向空间效应较为明显，虽然单梁法能粗略模拟结构的受力特性，但是无法明确反映宽箱钢箱梁桥的横向分布关系。梁格法是桥梁结构空间分析的一种有效方法，其计算结果更好地反映了宽箱钢箱梁桥的横向分布关系和受力特性。因此，針对宽箱钢箱梁桥，选用梁格模型时计算结果更为合理，也更便于根据不同梁段的受力特性进行截面优化设计。

（2）宽箱钢箱梁桥随着梁高的增加，跨中弯矩与支点剪力也逐渐增大。但是一味增加梁高并不利于此结构受力，设计中应结合实际情况，选用合适的梁高，避免浪费。

（3）对于端横梁长度较大的宽箱钢箱梁结构，应注意在荷载作用下，结构产生竖向变形，会导致中梁卸载，最中间梁上、下缘应力均最小，往边梁依次增加，该体系主要为边梁受力，增加中梁腹板及底板厚度对体系受力改善不明显，设计中应结合实际情况，对边梁、中梁的板厚进行不同取值，不但符合实际受力情况，而且节省了施工成本。

参考文献

[1]吴冲. 现代钢桥（上册）[M]. 北京：人民交通出版社， 2006.

[2]高丕勤， 王小松. 顶板横向预应力作用下宽箱梁空间效应分析[J]. 重庆交通大学学报（自然科学版）， 2012（S1）： 668-671.

[3]熊礼鹏. 宽箱连续钢箱梁桥支点横梁空间受力分析[J]. 交通科技， 2014（2）： 1-3.

[4]胡志礼. 横向大悬臂钢箱梁桥力学性能分析[J]. 城市道桥与防洪， 2013（2）： 34-36+8.

收稿日期：2023-12-15

作者简介：胡国栋（1991—），男，硕士研究生，工程师，从事桥梁设计工作。